程序框图课件(共30张PPT)2021届高考二轮考前复习数学文科
文档属性
| 名称 | 程序框图课件(共30张PPT)2021届高考二轮考前复习数学文科 |  | |
| 格式 | ppt | ||
| 文件大小 | 626.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-18 22:06:12 | ||
图片预览







文档简介
(共30张PPT)
程
序
框
图
真题再研析·提升审题力
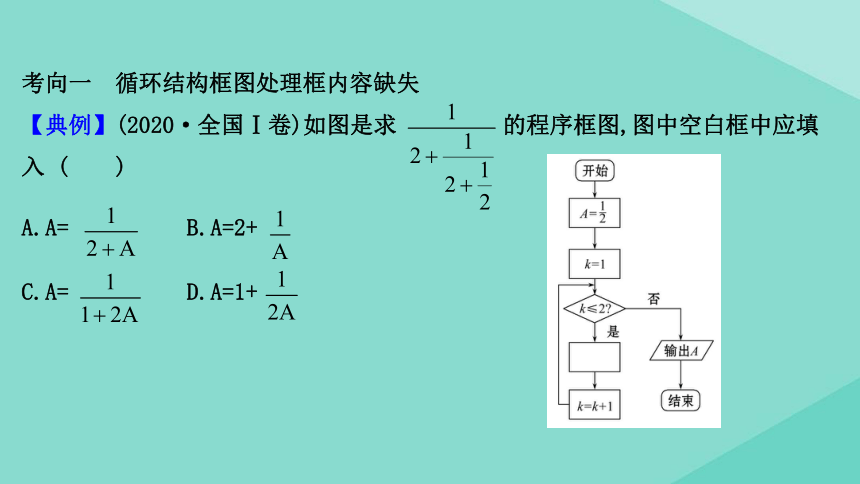
考向一 循环结构框图处理框内容缺失
【典例】(2020·全国Ⅰ卷)如图是求
的程序框图,图中空白框中应填
入
( )
A.A=
B.A=2+
C.A=
D.A=1+
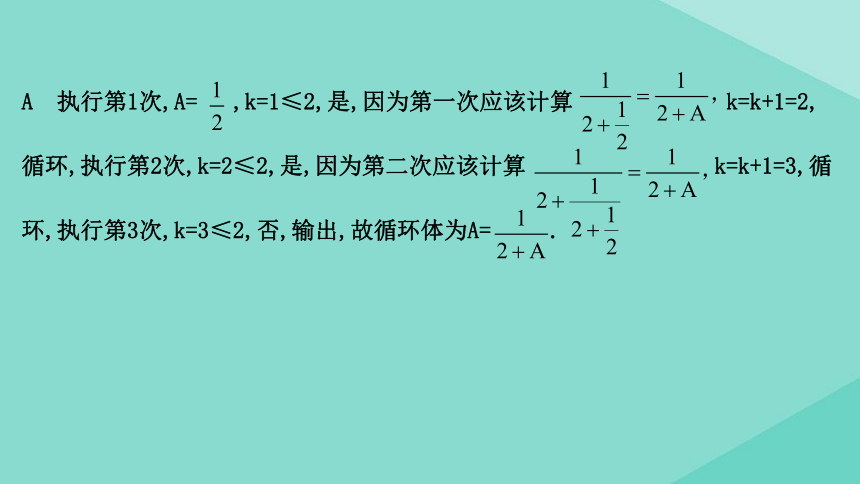
A 执行第1次,A=
,k=1≤2,是,因为第一次应该计算
k=k+1=2,
循环,执行第2次,k=2≤2,是,因为第二次应该计算
k=k+1=3,循
环,执行第3次,k=3≤2,否,输出,故循环体为A=
.
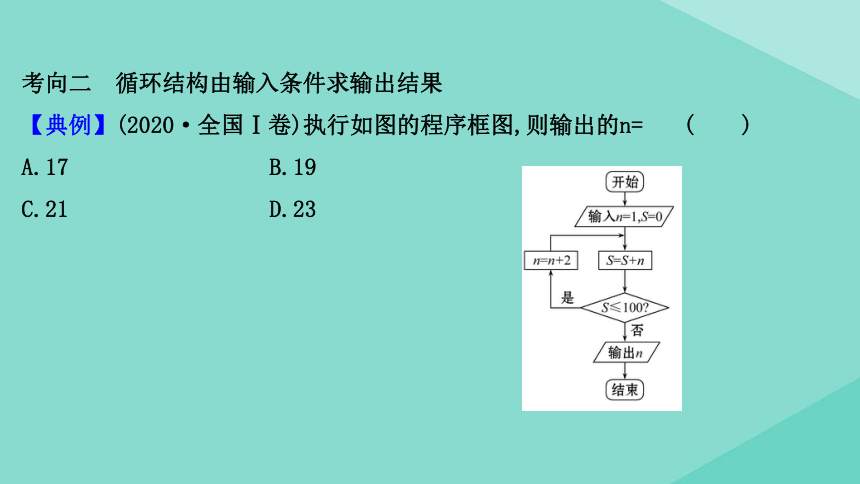
考向二 循环结构由输入条件求输出结果
【典例】(2020·全国Ⅰ卷)执行如图的程序框图,则输出的n=
( )
A.17
B.19
C.21
D.23
C 依据程序框图的算法功能可知,输出的n是满足1+3+5+…+n>100的最小正奇数,
因为1+3+5+…+n=
>100,解得n>19,所以输出的n=21.
【考前必备】
1.条件结构
判断框内的条件不同,对应的下一图框中的内容和操作要相应的进行变化,故要重点分析判断框内的条件是否满足.
2.循环结构
(1)确定循环次数:分析进入或退出循环体的条件,确定循环次数;
(2)完善程序框图:结合初始条件和输出结果,分析控制循环的变量应满足的条件或累加、累乘的变量的表达式;
(3)辨析循环结构的功能:执行程序若干次,即可判断.
【考场秘技】
1.循环结构题型的三点说明
(1)数列求和,一般是裂项相消求和;
(2)周期循环,一般循环次数较大时,四次循环或者五次循环为一个周期;
(3)循环之后得到某一计算公式,循环次数一般较少,按部就班的完成循环即可.
2.明晰循环起点条件、循环次数、循环终止条件.
3.明确流程图研究的数学问题,是求和还是求项.
【命题陷阱】
1.选择判断框内条件的题目,何时输出容易判断错误
【案例】T6
S=16,i=9,S=25,i=11,此时输出S,因而i=9不符合条件框的内容,但
i=11符合条件框内容.
2.循环框图处理框中含有等比数列通项或者裂项相消通项公式时,看不出该循环
结构为数列求和.
【案例】T9
S=S+
的含义为裂项相消求和,
可裂项为
即可求解.
3.条件结构框图中根据判断框条件作出判断时,容易出现错误.
【案例】T4
i是否为质数,下一步处理过程不同,判断失误导致最后结果错误.
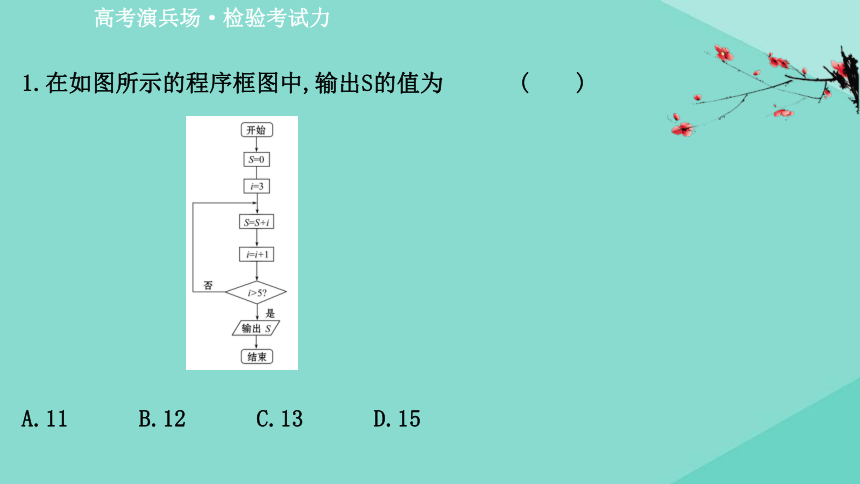
1.在如图所示的程序框图中,输出S的值为
( )
A.11 B.12 C.13 D.15
高考演兵场·检验考试力
B 通过第一次循环得到S=3,i=4;通过第二次循环得到S=7,i=5;通过第三次循环得到S=12,i=6;此时满足判断框中的条件i>5,执行输出S=12.
2.执行如图所示的程序框图,则输出的结果为
( )
A.31
B.39
C.47
D.60
D 根据题意,T=0,n=1;T=8,n=2;
T=8+4,n=3;T=8+4+4,n=4;
T=8+4+4+8,n=5;T=8+4+4+8+0,n=6;
T=8+4+4+8+0+12,n=7;
T=8+4+4+8+0+12-4,n=8;
T=8+4+4+8+0+12-4+16,n=9;
T=8+4+4+8+0+12-4+16-8,n=10;
T=8+4+4+8+0+12-4+16-8+20,n=11,
故输出的结果为T=8+4+4+8+0+12-4+16-8+20=60.
3.执行如图所示的程序框图,设输出数据构成集合A,从集合A中任取一个元素m,
则事件“函数f(x)=x2+mx在
上是增函数”的概率为
( )
A.
B.
C.
D.
C x=-2?y=0;x=-2+1=-1?y=-1;x=-1+1=0?y=0;x=0+1=1?y=3;
x=1+1=2?y=8;x=2+1=3,退出循环.所以A=
又函数f(x)=x2+mx在
上是增函数,所以-
≤0?m≥0.
故函数f(x)=x2+mx在
上是增函数的概率为
.
4.执行如图所示的程序框图,若输入t=4,则输出的i=
( )
A.16
B.13
C.10
D.7
A t=4,i=1,S=0,S(1)i=1不是质数,则S=0-1=-1,i=1+3=4,又-1<4,
(2)i=4不是质数,则S=-1-4=-5,i=4+3=7,又-5<4,
(3)i=7是质数,则S=-5+7=2,i=7+3=10,又2<4,
(4)i=10不是质数,则S=2-10=-8,i=10+3=13,又-8<4,
(5)i=13是质数,则S=-8+13=5,i=13+3=16,则5>4,所以输出i=16.
5.运行如图所示的程序框图,若输出S的值为248,则判断框中可以填
( )
A.n<3?
B.n<2?
C.n<4?
D.n<5?
A 运行该程序,第一次,S=27=128,n=6;第二次,S=128+26=192,n=5;第三次,S=192+25=224,n=4;第四次,S=224+24=240,n=3;第五次,S=240+23=248,n=2,此时,要想输出S的值,判断框中可以填n<3?.
6.阅读如图的程序框图,若输出的值为25,那么在程序框图中的判断框内可以填写的条件是
( )
A.i>5?
B.i>8?
C.i>10?
D.i>12?
C 根据程序框图可知,S=0,i=1
,则S=1,i=3,S=4,i=5,S=9,i=7,S=16,i=9,
S=25,i=11,此时输出S,因而i=9不符合条件框的内容,但i=11符合条件框内容,结合选项可知C为正确选项.
7.执行如图所示的程序框图,则输出k的值为
( )
A.4
B.5
C.6
D.7
C 观察分析题中所给的框图,可以发现s=
×…,结合条件,可知最后输
出的k的值为6.
8.执行如图所示的程序框图,输入的n值为4,则S=
( )
A.6
B.14
C.30
D.2
B k=1,S=0,
1<4成立,第一次循环,S=2,k=1+1=2,
第二次循环,2<4成立,S=2+22=2+4=6,k=2+1=3,
第三次循环,3<4成立,S=6+23=6+8=14,k=3+1=4,
第四次循环,4<4不成立,则输出S=14.
9.如果执行如图所示的框图,输入N=5,则输出的数等于
( )
A.
B.
C.
D.
D 当N=5时,该程序框图所表示的算法功能为求S=
的值.原式=1-
=
.
10.运行如图所示的程序框图,若输出S的值为35,则判断框中可以填
( )
A.i≥4?
B.i≥5?
C.i≥6?
D.i≥7?
B i=1,n=1,S=1,进入判断框,执行循环体;
i=2,n=3,S=4,进入判断框,执行循环体;
i=3,n=6,S=10,进入判断框,执行循环体;
i=4,n=10,S=20,进入判断框,执行循环体;
i=5,n=15,S=35,进入判断框,终止循环,输出S的值;
所以判断框中可以填i≥5?.
程
序
框
图
真题再研析·提升审题力
考向一 循环结构框图处理框内容缺失
【典例】(2020·全国Ⅰ卷)如图是求
的程序框图,图中空白框中应填
入
( )
A.A=
B.A=2+
C.A=
D.A=1+
A 执行第1次,A=
,k=1≤2,是,因为第一次应该计算
k=k+1=2,
循环,执行第2次,k=2≤2,是,因为第二次应该计算
k=k+1=3,循
环,执行第3次,k=3≤2,否,输出,故循环体为A=
.
考向二 循环结构由输入条件求输出结果
【典例】(2020·全国Ⅰ卷)执行如图的程序框图,则输出的n=
( )
A.17
B.19
C.21
D.23
C 依据程序框图的算法功能可知,输出的n是满足1+3+5+…+n>100的最小正奇数,
因为1+3+5+…+n=
>100,解得n>19,所以输出的n=21.
【考前必备】
1.条件结构
判断框内的条件不同,对应的下一图框中的内容和操作要相应的进行变化,故要重点分析判断框内的条件是否满足.
2.循环结构
(1)确定循环次数:分析进入或退出循环体的条件,确定循环次数;
(2)完善程序框图:结合初始条件和输出结果,分析控制循环的变量应满足的条件或累加、累乘的变量的表达式;
(3)辨析循环结构的功能:执行程序若干次,即可判断.
【考场秘技】
1.循环结构题型的三点说明
(1)数列求和,一般是裂项相消求和;
(2)周期循环,一般循环次数较大时,四次循环或者五次循环为一个周期;
(3)循环之后得到某一计算公式,循环次数一般较少,按部就班的完成循环即可.
2.明晰循环起点条件、循环次数、循环终止条件.
3.明确流程图研究的数学问题,是求和还是求项.
【命题陷阱】
1.选择判断框内条件的题目,何时输出容易判断错误
【案例】T6
S=16,i=9,S=25,i=11,此时输出S,因而i=9不符合条件框的内容,但
i=11符合条件框内容.
2.循环框图处理框中含有等比数列通项或者裂项相消通项公式时,看不出该循环
结构为数列求和.
【案例】T9
S=S+
的含义为裂项相消求和,
可裂项为
即可求解.
3.条件结构框图中根据判断框条件作出判断时,容易出现错误.
【案例】T4
i是否为质数,下一步处理过程不同,判断失误导致最后结果错误.
1.在如图所示的程序框图中,输出S的值为
( )
A.11 B.12 C.13 D.15
高考演兵场·检验考试力
B 通过第一次循环得到S=3,i=4;通过第二次循环得到S=7,i=5;通过第三次循环得到S=12,i=6;此时满足判断框中的条件i>5,执行输出S=12.
2.执行如图所示的程序框图,则输出的结果为
( )
A.31
B.39
C.47
D.60
D 根据题意,T=0,n=1;T=8,n=2;
T=8+4,n=3;T=8+4+4,n=4;
T=8+4+4+8,n=5;T=8+4+4+8+0,n=6;
T=8+4+4+8+0+12,n=7;
T=8+4+4+8+0+12-4,n=8;
T=8+4+4+8+0+12-4+16,n=9;
T=8+4+4+8+0+12-4+16-8,n=10;
T=8+4+4+8+0+12-4+16-8+20,n=11,
故输出的结果为T=8+4+4+8+0+12-4+16-8+20=60.
3.执行如图所示的程序框图,设输出数据构成集合A,从集合A中任取一个元素m,
则事件“函数f(x)=x2+mx在
上是增函数”的概率为
( )
A.
B.
C.
D.
C x=-2?y=0;x=-2+1=-1?y=-1;x=-1+1=0?y=0;x=0+1=1?y=3;
x=1+1=2?y=8;x=2+1=3,退出循环.所以A=
又函数f(x)=x2+mx在
上是增函数,所以-
≤0?m≥0.
故函数f(x)=x2+mx在
上是增函数的概率为
.
4.执行如图所示的程序框图,若输入t=4,则输出的i=
( )
A.16
B.13
C.10
D.7
A t=4,i=1,S=0,S
(2)i=4不是质数,则S=-1-4=-5,i=4+3=7,又-5<4,
(3)i=7是质数,则S=-5+7=2,i=7+3=10,又2<4,
(4)i=10不是质数,则S=2-10=-8,i=10+3=13,又-8<4,
(5)i=13是质数,则S=-8+13=5,i=13+3=16,则5>4,所以输出i=16.
5.运行如图所示的程序框图,若输出S的值为248,则判断框中可以填
( )
A.n<3?
B.n<2?
C.n<4?
D.n<5?
A 运行该程序,第一次,S=27=128,n=6;第二次,S=128+26=192,n=5;第三次,S=192+25=224,n=4;第四次,S=224+24=240,n=3;第五次,S=240+23=248,n=2,此时,要想输出S的值,判断框中可以填n<3?.
6.阅读如图的程序框图,若输出的值为25,那么在程序框图中的判断框内可以填写的条件是
( )
A.i>5?
B.i>8?
C.i>10?
D.i>12?
C 根据程序框图可知,S=0,i=1
,则S=1,i=3,S=4,i=5,S=9,i=7,S=16,i=9,
S=25,i=11,此时输出S,因而i=9不符合条件框的内容,但i=11符合条件框内容,结合选项可知C为正确选项.
7.执行如图所示的程序框图,则输出k的值为
( )
A.4
B.5
C.6
D.7
C 观察分析题中所给的框图,可以发现s=
×…,结合条件,可知最后输
出的k的值为6.
8.执行如图所示的程序框图,输入的n值为4,则S=
( )
A.6
B.14
C.30
D.2
B k=1,S=0,
1<4成立,第一次循环,S=2,k=1+1=2,
第二次循环,2<4成立,S=2+22=2+4=6,k=2+1=3,
第三次循环,3<4成立,S=6+23=6+8=14,k=3+1=4,
第四次循环,4<4不成立,则输出S=14.
9.如果执行如图所示的框图,输入N=5,则输出的数等于
( )
A.
B.
C.
D.
D 当N=5时,该程序框图所表示的算法功能为求S=
的值.原式=1-
=
.
10.运行如图所示的程序框图,若输出S的值为35,则判断框中可以填
( )
A.i≥4?
B.i≥5?
C.i≥6?
D.i≥7?
B i=1,n=1,S=1,进入判断框,执行循环体;
i=2,n=3,S=4,进入判断框,执行循环体;
i=3,n=6,S=10,进入判断框,执行循环体;
i=4,n=10,S=20,进入判断框,执行循环体;
i=5,n=15,S=35,进入判断框,终止循环,输出S的值;
所以判断框中可以填i≥5?.
同课章节目录
