统计与概率课件(共48张PPT)2021届高考二轮考前复习数学文科
文档属性
| 名称 | 统计与概率课件(共48张PPT)2021届高考二轮考前复习数学文科 |  | |
| 格式 | ppt | ||
| 文件大小 | 611.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-18 22:06:31 | ||
图片预览










文档简介
(共48张PPT)
统计与概率
真题再研析·提升审题力
【典例】(12分)(2020·全国Ⅰ卷)某厂接受了一项加工业务,加工出来的产品(单位:件)按标准分为A,B,C,D四个等级.加工业务约定:对于A级品、B级品、C级品,厂家每件分别收取加工费90元,50元,20元;对于D级品,厂家每件要赔偿原料损失费50元.该厂有甲、乙两个分厂可承接加工业务.甲分厂加工成本费为25元/件,乙分厂加工成本费为20元/件.厂家为决定由哪个分厂承接加工业务,在两个分厂各试加工了100件这种产品,并统计了这些产品的等级,整理如下:
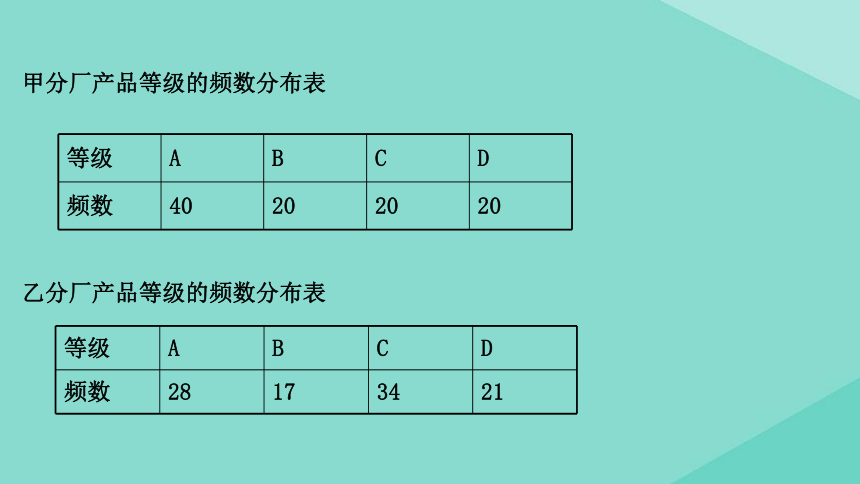
甲分厂产品等级的频数分布表
乙分厂产品等级的频数分布表
等级
A
B
C
D
频数
40
20
20
20
等级
A
B
C
D
频数
28
17
34
21
(1)分别估计甲、乙两分厂加工出来的一件产品为A级品的概率;
(2)分别求甲、乙两分厂加工出来的100件产品的平均利润,以平均利润为依据,厂家应选哪个分厂承接加工业务?
【审题·逆向思维】
(1)A级品的概率?频数分布表;
(2)方案选择?平均利润?甲、乙两分厂分别加工100件产品的总利润.
【标准答案】
(1)由表可知,甲分厂加工出来的一件产品为A级品的概率估计值为
=0.4,
·································3分
乙分厂加工出来的一件产品为A级品的概率估计值为
=0.28.·····6分
(2)甲分厂加工100件产品总利润为40×
+20×
+20×
-20×
=1
500元,所以甲分厂加工100件产品的平均利润为15元/件;
································9分
乙分厂加工100件产品的总利润为
28×
+17×
+34×
-21×
=1
000元,
所以乙分厂加工100件产品的平均利润为10元/件.··········
11分
故厂家应选择甲分厂承接加工任务.················12分
【深度解读】
测试
目标
(1)直接运用公式解决问题;
(2)平均值的求法.
测试
目标
数据分析:通过分析数据求出平均值;
数学运算:运用公式,由频数估计概率.
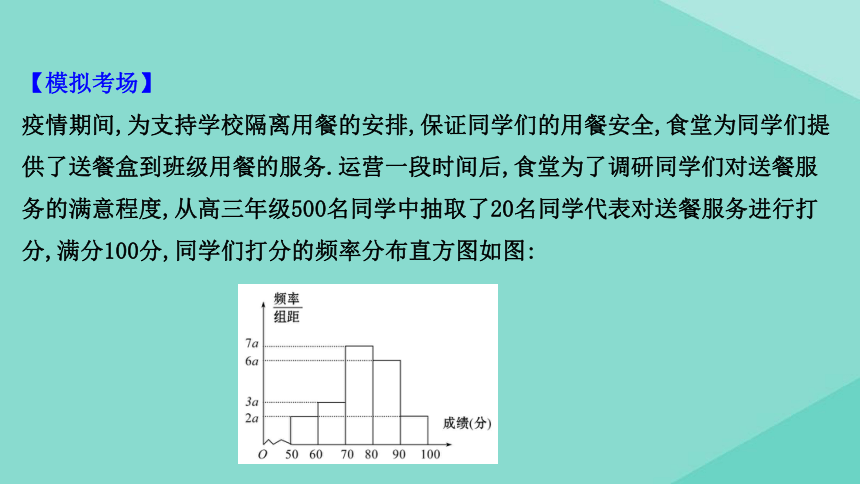
【模拟考场】
疫情期间,为支持学校隔离用餐的安排,保证同学们的用餐安全,食堂为同学们提供了送餐盒到班级用餐的服务.运营一段时间后,食堂为了调研同学们对送餐服务的满意程度,从高三年级500名同学中抽取了20名同学代表对送餐服务进行打分,满分100分,同学们打分的频率分布直方图如图:
(1)求频率分布直方图中a的值;
(2)从成绩在
的学生中任选2人,求此2人的成绩都在
中的概率;
(3)若打分不低于60分可视为对送餐服务满意,用样本的统计结果估计总体,请估
计全年级有多少同学对送餐服务满意.
【解析】(1)因为2a+2a+3a+6a+7a=20a,所以20a×10=1,所以a=0.005.
(2)成绩在
的人数=2×0.005×10×20=2,成绩在
中的学生人数
=3×0.005×10×20=3,用a,b表示成绩在
的2名学生,用c,d,e表示成绩在
的3名学生,从5人中任取2人,有ab,ac,ad,ae,bc,bd,be,cd,ce,de,共10
种情形.符合条件的有3种(cd,ce,de),
所以概率P=
.
(3)样本20人中有18人打分成绩不低于60分,即有
的学生对送餐服务满意.用
样本的统计结果估计总体,则估计全年级500人中,有500×
=450人对送餐服务
满意.
【考场秘技】
1.频率分布直方图中的数字特征
(1)最高的小长方形底边中点的横坐标即是众数;
(2)中位数左边和右边的小长方形的面积和是相等的;
(3)平均数等于频率分布直方图中每个小长方形的面积乘以小长方形底边中点的横坐标之和.
2.古典概型的两个特征
(1)试验的所有可能结果只有有限个,每次试验只出现其中的一个结果;
(2)每一个试验结果出现的可能性相同.
3.互斥事件概率的加法公式
(1)如果事件A与事件B互斥,
则
(2)若事件B与事件A互为对立事件,
则P
=1-P
.
4.互斥事件与对立事件的概念
(1)互斥事件是不可能同时发生的事件,但可以同时不发生;
(2)对立事件是特殊的互斥事件,特殊在对立的两个事件不可能都不发生(或都发
生),即有且仅有一个发生.
5.求复杂的互斥事件的概率的两种方法
(1)直接求解法:将所求事件的概率分解为一些彼此互斥的事件的概率,再求和;
(2)间接法:先求该事件的对立事件的概率,再由P
=1-P
求解.
当题目涉及“至多”“至少”型问题时,多考虑间接法.
【万能模板】
求古典概型概率的基本步骤
第一步:将题目条件中的相关内容转化为事件;
第二步:判断事件是否为古典概型;
第三步:选用合适的方法确定基本事件个数;
第四步:代入古典概型的概率公式求解.
【阅卷点评】
1.步骤分:(1)由频数求频率公式不能缺少;(2)平均值的公式不能少.
2.关键分:解题过程的关键点,有则给分,无则没分.如平均值公式,不能缺少.
3.计算分:概率计算要保证正确.
1.(方案设计)某企业对某种产品的生产线进行了改造升级,已知该种产品的质量以其质量指标值m衡量,并依据质量指标值m划分等级如表:
高考演兵场·检验考试力
质量指
标值m
300≤m
<350
250≤m<300
或350≤m<400
150≤m<250
或400≤m<450
等级
一等品
二等品
三等品
该企业从生产的这种产品中随机抽取100件产品作为样本,检测其质量指标值,得到如图的频率分布直方图.
(1)根据频率分布直方图估计这100件产品的质量指标值m的平均数
(同一区间
数据用该区间数据的中点值代表);
(2)用分层抽样的方法从样本质量指标值m在区间
和
内的产
品中随机抽取4件,再从这4件中任取2件进一步研究,求这2件都取自区间
内的概率;
(3)该企业统计了近100天中每天的生产件数,得下面的频数分布表:
件数
[5
500,6
500)
[6
500,7
500)
[7
500,8
500)
[8
500,9
500]
天数
20
30
40
10
该企业计划引进新的设备对该产品进行进一步加工,有A,B两种设备可供选择.A设备每台每天最多可以加工30件,每天维护费用为500元/台;B设备每台每天最多可以加工4件,每天维护费用为80元/台.该企业现有两种购置方案:
方案一:购买100台A设备和800台B设备;
方案二:购买200台A设备和450台B设备.
假设进一步加工后每件产品可以增加25元的收入,在抽取的这100天的生产件数(同一组数据用该区间数据的中点值代表)的前提下,试依据使用A,B两种设备后的日增加的利润(日增加的利润=日增加的收入-日维护费用)的均值为该公司决策,选择哪种方案更好?
【解析】(1)由题意得
=175×0.05+225×0.15+275×0.2+325×0.3+375×0.2+425×0.1=312.5.
(2)因为区间
和
内的产品的频率之比为1∶3,
所以应从区间
内抽取1件,记为A1,从区间
内抽取3件,记为
B1,B2,B3,则从中任取2件的情况有
共6种,其中2件都取自区间
内的情况有
共3种,
所以其概率P=
(3)每天生产件数的频数分布表为:
件数
6
000
7
000
8
000
9
000
天数
20
30
40
10
若采用方案一,使用100台A设备和800台B设备每天可进一步加工的件数为
30×100+4×800=6
200,可得实际加工件数的频数分布表为
所以方案一中使用A,B设备进一步加工后的日增加的利润均值为25×
-500×100-80×800=40
000;
实际加工件数
6
000
6
200
频数
20
80
若采用方案二,使用200台A设备和450台B设备每天可进一步加工的件数为
30×200+4×450=7
800,可得实际加工件数的频数分布表为
所以方案二中使用A,B设备进一步加工后的日增加的利润均值为
25×
-500×200-80×450=44
000.
综上所述,公司应该选择方案二更好.
实际加工件数
6
000
7
000
7
800
频数
20
30
50
2.(成绩分析)参加市数学调研抽测的某校高三学生成绩分析的茎叶图和频率分布直方图均受到不同程度的破坏,但可见部分信息如下,据此解答如下问题:
(1)求参加数学抽测的人数n、抽测成绩的中位数及分数分别在
内的人数;
(2)若从分数在
内的学生中任选两人进行调研谈话,求恰好有一人分数在
内的概率.
【解析】(1)分数在
内的频数为2,由频率分布直方图可以看出,分数在
内同样有2人.
由
=10×0.008,得n=25,
由茎叶图可知抽测成绩的中位数为73.
分数在
内的人数为25-
=4,
参加数学抽测的人数n=25,中位数为73,分数
内的人数分别为4人、
2人.
(2)设“从分数在
内的学生中任选两人,恰好有一人分数在
内”
为事件M,将
内的4人编号为a,b,c,d;
内的2人编号为A,B,
在
内任取两人的基本事件为:ab,ac,ad,aA,aB,bc,bd,bA,bB,cd,cA,
cB,dA,dB,AB,共15个,其中,恰好有一人分数在
内的基本事件有
aA,aB,bA,bB,cA,cB,dA,dB,共8个,故所求的概率P(M)=
.
3.(运动状况)某校高一、高二两个年级共336名学生同时参与了跳绳、踢毽两项健身活动,为了了解学生的运动状况,采用样本按比例分配的分层抽样方法,从高一、高二两个年级的学生中分别抽取7名和5名学生进行测试,如表是高二年级的5名学生的测试数据(单位:个/分钟)
学生编号
1
2
3
4
5
跳绳个数
179
181
170
177
183
踢毽个数
82
76
79
73
80
(1)求高一、高二两个年级各有多少人?
(2)从高二年级的学生中任选一人,试估计该学生每分钟跳绳个数超过175且踢毽个数超过75的概率;
(3)高二年级学生的两项运动的成绩哪项更稳定?
【解析】(1)高一年级的学生人数为336×
=196.
高二年级的学生人数为336×
=140.
(2)设“该学生每分钟跳绳个数超过175且踢毽个数超过75”为事件A,
由表中的数据可知:
高二年级选出的5名学生中每分钟跳绳个数超过175且踢毽个数超过75的共有3人,
所以从5人中任选一人,事件A发生的概率为
,
由此估计从高二年级的学生中任选一人,事件A发生的概率为
.
(3)由表中的数据可以估计:
高二年级的学生每分钟跳绳的个数的平均数为
×(179+181+170+177+183)=178.
高二年级的学生每分钟跳绳的个数的方差为
×[(179-178)2+(181-178)2
+(170-178)2+(177-178)2+(183-178)2]=20.
高二年级的学生每分钟踢毽的个数的平均数为
×(82+76+79+73+80)=78.
高二年级的学生每分钟踢毽的个数的方差为
×[(82-78)2+(76-78)2
+(79-78)2+(73-78)2+(80-78)2]=10,
由于
,所以高二年级学生的踢毽的成绩更稳定.
4.(节约用水)我国是世界上严重缺水的国家,城市缺水问题较为突出.某市政府为了鼓励居民节约用水,计划在本市试行居民生活用水定额管理,即确定一个合理的居民月用水量标准x(吨),月用水量不超过x的部分按平价收费,超出x的部分按议价收费.为了了解全市居民用水量的分布情况,通过抽样,获得了100位居民某年的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.
(1)求频率分布直方图中a的值.
(2)已知该市有80万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由.
(3)若该市政府希望使85%的居民每月的用水量不超过标准x(吨),估计x的值,并说明理由.
【解析】(1)由频率分布直方图,可得(0.08+0.16+a+0.40+0.52+a+0.12+0.08+0.04)×0.5=1,
解得a=0.30.
(2)用频率估计概率,由题可知80×0.5×(0.04+0.08+
0.12)=9.6,
所以全市居民中月均用水量不低于3吨的约为9.6万人.
(3)因为前6组的频率之和为(0.08+0.16+0.30+0.40+0.52+0.30)
×0.5=0.88>0.85,而前5组的频率之和为
(0.08+0.16+0.30+0.40+0.52)×0.5=0.73<0.85,所以2.5≤x<3.
由0.3×(x-2.5)=0.85-0.73,解得x=2.9.
因此,估计月用水量标准为2.9吨时,85%的居民每月的用水量不超过标准.
5.(文化自信)某动漫影视制作公司长期坚持文化自信,不断挖掘中华优秀传统文化中的动漫题材,创作出一批又一批的优秀动漫影视作品,获得市场和广大观众的一致好评,同时也为公司赢得丰厚的利润.该公司2013年至2019年的年利润y关于年份代号x的统计数据如表(已知该公司的年利润与年份代号线性相关):
年份
2013
2014
2015
2016
2017
2018
2019
年份代号x
1
2
3
4
5
6
7
年利润y
(单位:亿元)
29
33
36
44
48
52
59
(1)求y关于x的线性回归方程,并预测该公司2020年(年份代号记为8)的年利润;
(2)当统计表中某年年利润的实际值大于由(1)中线性回归方程计算出该年利润的估计值时,称该年为A级利润年,否则称为B级利润年.将(1)中预测的该公司2020年的年利润视作该年利润的实际值,现从2015年至2020年这6年中随机抽取2年,求恰有1年为A级利润年的概率.
【解析】(1)根据表中数据,计算可得
=4,
=43,
又
=28,
所以
因为
,所以
=43-5×4=23,
所以y关于x的线性回归方程为
=5x+23.
将x=8代入,得
=5×8+23=63.
所以该公司2020年的年利润的预测值为63亿元.
(2)由(1)可知2015年至2020年的年利润的估计值分别为38,43,48,53,58,63(单位:亿元),
其中实际利润大于相应估计值的有2年.
故这6年中,被评为A级利润年的有2年,分别记为A1,A2;
评为B级利润年的有4年,分别记为B1,B2,B3,B4,
从2015年至2020年中随机抽取2年,总的情况分别为:
A1A2,A1B1,A1B2,A1B3,A1B4,A2B1,A2B2,A2B3,A2B4,B1B2,B1B3,B1B4,B2B3,B2B4,B3B4,
共计15种情况.
其中恰有一年为A级利润年的情况分别为:A1B1,A1B2,A1B3,A1B4,A2B1,A2B2,A2B3,A2B4共有8种情况.
记“从2015年至2020年这6年的年利润中随机抽取2年,恰有一年为A级利润年”
的概率为P,故所求概率P=
.
6.(成绩分析)某校高一年级1
000名学生期中考试生物学科成绩的频率分布直方图如图所示,其中成绩分组情况如表:
组号
第一组
第二组
第三组
第四组
第五组
分组
[50,60)
[60,70)
[70,80)
[80,90)
[90,100]
(1)求生物成绩在[50,60)内的人数;
(2)若同组中的每个数据用该组区间中点值代替,根据频率分布直方图,估计这
1
000名学生生物成绩的平均分;
(3)现有5名同学,其中3人的成绩在第三组内,2人的成绩在第四组内,从这5名同学中随机抽取2名,求这2名同学来自不同组的概率.
【解析】(1)由题意,生物成绩在
内的频率为
1-(0.01×10+0.02×10+0.03×10+0.035×10)=0.05,
所以生物成绩在
内的人数为0.05×1
000=50.
(2)由频率分布直方图得,分数在[50,60)内的频率为0.05,[60,70)内的频率为
0.35,[70,80)内的频率为0.3,[80,90)内的频率为0.2,[90,100]内的频率为0.1,
所以这1
000名学生期中考试生物成绩的平均分的估计值为:55×0.05+65×0.35+75×0.3+85×0.2+95×0.1=74.5.
(3)设“这2名同学来自不同组”为事件A,设第三组的3名同学为a,b,c,
第四组的2名同学为x,y,则样本空间为Ω={(a,b),(a,c),(a,x),(a,y),(b,c),(b,x),(b,y),(c,x),(c,y),(x,y)},
事件A={(a,x),(a,y),(b,x),(b,y),(c,x),(c,y)}.
所以P(A)=
统计与概率
真题再研析·提升审题力
【典例】(12分)(2020·全国Ⅰ卷)某厂接受了一项加工业务,加工出来的产品(单位:件)按标准分为A,B,C,D四个等级.加工业务约定:对于A级品、B级品、C级品,厂家每件分别收取加工费90元,50元,20元;对于D级品,厂家每件要赔偿原料损失费50元.该厂有甲、乙两个分厂可承接加工业务.甲分厂加工成本费为25元/件,乙分厂加工成本费为20元/件.厂家为决定由哪个分厂承接加工业务,在两个分厂各试加工了100件这种产品,并统计了这些产品的等级,整理如下:
甲分厂产品等级的频数分布表
乙分厂产品等级的频数分布表
等级
A
B
C
D
频数
40
20
20
20
等级
A
B
C
D
频数
28
17
34
21
(1)分别估计甲、乙两分厂加工出来的一件产品为A级品的概率;
(2)分别求甲、乙两分厂加工出来的100件产品的平均利润,以平均利润为依据,厂家应选哪个分厂承接加工业务?
【审题·逆向思维】
(1)A级品的概率?频数分布表;
(2)方案选择?平均利润?甲、乙两分厂分别加工100件产品的总利润.
【标准答案】
(1)由表可知,甲分厂加工出来的一件产品为A级品的概率估计值为
=0.4,
·································3分
乙分厂加工出来的一件产品为A级品的概率估计值为
=0.28.·····6分
(2)甲分厂加工100件产品总利润为40×
+20×
+20×
-20×
=1
500元,所以甲分厂加工100件产品的平均利润为15元/件;
································9分
乙分厂加工100件产品的总利润为
28×
+17×
+34×
-21×
=1
000元,
所以乙分厂加工100件产品的平均利润为10元/件.··········
11分
故厂家应选择甲分厂承接加工任务.················12分
【深度解读】
测试
目标
(1)直接运用公式解决问题;
(2)平均值的求法.
测试
目标
数据分析:通过分析数据求出平均值;
数学运算:运用公式,由频数估计概率.
【模拟考场】
疫情期间,为支持学校隔离用餐的安排,保证同学们的用餐安全,食堂为同学们提供了送餐盒到班级用餐的服务.运营一段时间后,食堂为了调研同学们对送餐服务的满意程度,从高三年级500名同学中抽取了20名同学代表对送餐服务进行打分,满分100分,同学们打分的频率分布直方图如图:
(1)求频率分布直方图中a的值;
(2)从成绩在
的学生中任选2人,求此2人的成绩都在
中的概率;
(3)若打分不低于60分可视为对送餐服务满意,用样本的统计结果估计总体,请估
计全年级有多少同学对送餐服务满意.
【解析】(1)因为2a+2a+3a+6a+7a=20a,所以20a×10=1,所以a=0.005.
(2)成绩在
的人数=2×0.005×10×20=2,成绩在
中的学生人数
=3×0.005×10×20=3,用a,b表示成绩在
的2名学生,用c,d,e表示成绩在
的3名学生,从5人中任取2人,有ab,ac,ad,ae,bc,bd,be,cd,ce,de,共10
种情形.符合条件的有3种(cd,ce,de),
所以概率P=
.
(3)样本20人中有18人打分成绩不低于60分,即有
的学生对送餐服务满意.用
样本的统计结果估计总体,则估计全年级500人中,有500×
=450人对送餐服务
满意.
【考场秘技】
1.频率分布直方图中的数字特征
(1)最高的小长方形底边中点的横坐标即是众数;
(2)中位数左边和右边的小长方形的面积和是相等的;
(3)平均数等于频率分布直方图中每个小长方形的面积乘以小长方形底边中点的横坐标之和.
2.古典概型的两个特征
(1)试验的所有可能结果只有有限个,每次试验只出现其中的一个结果;
(2)每一个试验结果出现的可能性相同.
3.互斥事件概率的加法公式
(1)如果事件A与事件B互斥,
则
(2)若事件B与事件A互为对立事件,
则P
=1-P
.
4.互斥事件与对立事件的概念
(1)互斥事件是不可能同时发生的事件,但可以同时不发生;
(2)对立事件是特殊的互斥事件,特殊在对立的两个事件不可能都不发生(或都发
生),即有且仅有一个发生.
5.求复杂的互斥事件的概率的两种方法
(1)直接求解法:将所求事件的概率分解为一些彼此互斥的事件的概率,再求和;
(2)间接法:先求该事件的对立事件的概率,再由P
=1-P
求解.
当题目涉及“至多”“至少”型问题时,多考虑间接法.
【万能模板】
求古典概型概率的基本步骤
第一步:将题目条件中的相关内容转化为事件;
第二步:判断事件是否为古典概型;
第三步:选用合适的方法确定基本事件个数;
第四步:代入古典概型的概率公式求解.
【阅卷点评】
1.步骤分:(1)由频数求频率公式不能缺少;(2)平均值的公式不能少.
2.关键分:解题过程的关键点,有则给分,无则没分.如平均值公式,不能缺少.
3.计算分:概率计算要保证正确.
1.(方案设计)某企业对某种产品的生产线进行了改造升级,已知该种产品的质量以其质量指标值m衡量,并依据质量指标值m划分等级如表:
高考演兵场·检验考试力
质量指
标值m
300≤m
<350
250≤m<300
或350≤m<400
150≤m<250
或400≤m<450
等级
一等品
二等品
三等品
该企业从生产的这种产品中随机抽取100件产品作为样本,检测其质量指标值,得到如图的频率分布直方图.
(1)根据频率分布直方图估计这100件产品的质量指标值m的平均数
(同一区间
数据用该区间数据的中点值代表);
(2)用分层抽样的方法从样本质量指标值m在区间
和
内的产
品中随机抽取4件,再从这4件中任取2件进一步研究,求这2件都取自区间
内的概率;
(3)该企业统计了近100天中每天的生产件数,得下面的频数分布表:
件数
[5
500,6
500)
[6
500,7
500)
[7
500,8
500)
[8
500,9
500]
天数
20
30
40
10
该企业计划引进新的设备对该产品进行进一步加工,有A,B两种设备可供选择.A设备每台每天最多可以加工30件,每天维护费用为500元/台;B设备每台每天最多可以加工4件,每天维护费用为80元/台.该企业现有两种购置方案:
方案一:购买100台A设备和800台B设备;
方案二:购买200台A设备和450台B设备.
假设进一步加工后每件产品可以增加25元的收入,在抽取的这100天的生产件数(同一组数据用该区间数据的中点值代表)的前提下,试依据使用A,B两种设备后的日增加的利润(日增加的利润=日增加的收入-日维护费用)的均值为该公司决策,选择哪种方案更好?
【解析】(1)由题意得
=175×0.05+225×0.15+275×0.2+325×0.3+375×0.2+425×0.1=312.5.
(2)因为区间
和
内的产品的频率之比为1∶3,
所以应从区间
内抽取1件,记为A1,从区间
内抽取3件,记为
B1,B2,B3,则从中任取2件的情况有
共6种,其中2件都取自区间
内的情况有
共3种,
所以其概率P=
(3)每天生产件数的频数分布表为:
件数
6
000
7
000
8
000
9
000
天数
20
30
40
10
若采用方案一,使用100台A设备和800台B设备每天可进一步加工的件数为
30×100+4×800=6
200,可得实际加工件数的频数分布表为
所以方案一中使用A,B设备进一步加工后的日增加的利润均值为25×
-500×100-80×800=40
000;
实际加工件数
6
000
6
200
频数
20
80
若采用方案二,使用200台A设备和450台B设备每天可进一步加工的件数为
30×200+4×450=7
800,可得实际加工件数的频数分布表为
所以方案二中使用A,B设备进一步加工后的日增加的利润均值为
25×
-500×200-80×450=44
000.
综上所述,公司应该选择方案二更好.
实际加工件数
6
000
7
000
7
800
频数
20
30
50
2.(成绩分析)参加市数学调研抽测的某校高三学生成绩分析的茎叶图和频率分布直方图均受到不同程度的破坏,但可见部分信息如下,据此解答如下问题:
(1)求参加数学抽测的人数n、抽测成绩的中位数及分数分别在
内的人数;
(2)若从分数在
内的学生中任选两人进行调研谈话,求恰好有一人分数在
内的概率.
【解析】(1)分数在
内的频数为2,由频率分布直方图可以看出,分数在
内同样有2人.
由
=10×0.008,得n=25,
由茎叶图可知抽测成绩的中位数为73.
分数在
内的人数为25-
=4,
参加数学抽测的人数n=25,中位数为73,分数
内的人数分别为4人、
2人.
(2)设“从分数在
内的学生中任选两人,恰好有一人分数在
内”
为事件M,将
内的4人编号为a,b,c,d;
内的2人编号为A,B,
在
内任取两人的基本事件为:ab,ac,ad,aA,aB,bc,bd,bA,bB,cd,cA,
cB,dA,dB,AB,共15个,其中,恰好有一人分数在
内的基本事件有
aA,aB,bA,bB,cA,cB,dA,dB,共8个,故所求的概率P(M)=
.
3.(运动状况)某校高一、高二两个年级共336名学生同时参与了跳绳、踢毽两项健身活动,为了了解学生的运动状况,采用样本按比例分配的分层抽样方法,从高一、高二两个年级的学生中分别抽取7名和5名学生进行测试,如表是高二年级的5名学生的测试数据(单位:个/分钟)
学生编号
1
2
3
4
5
跳绳个数
179
181
170
177
183
踢毽个数
82
76
79
73
80
(1)求高一、高二两个年级各有多少人?
(2)从高二年级的学生中任选一人,试估计该学生每分钟跳绳个数超过175且踢毽个数超过75的概率;
(3)高二年级学生的两项运动的成绩哪项更稳定?
【解析】(1)高一年级的学生人数为336×
=196.
高二年级的学生人数为336×
=140.
(2)设“该学生每分钟跳绳个数超过175且踢毽个数超过75”为事件A,
由表中的数据可知:
高二年级选出的5名学生中每分钟跳绳个数超过175且踢毽个数超过75的共有3人,
所以从5人中任选一人,事件A发生的概率为
,
由此估计从高二年级的学生中任选一人,事件A发生的概率为
.
(3)由表中的数据可以估计:
高二年级的学生每分钟跳绳的个数的平均数为
×(179+181+170+177+183)=178.
高二年级的学生每分钟跳绳的个数的方差为
×[(179-178)2+(181-178)2
+(170-178)2+(177-178)2+(183-178)2]=20.
高二年级的学生每分钟踢毽的个数的平均数为
×(82+76+79+73+80)=78.
高二年级的学生每分钟踢毽的个数的方差为
×[(82-78)2+(76-78)2
+(79-78)2+(73-78)2+(80-78)2]=10,
由于
,所以高二年级学生的踢毽的成绩更稳定.
4.(节约用水)我国是世界上严重缺水的国家,城市缺水问题较为突出.某市政府为了鼓励居民节约用水,计划在本市试行居民生活用水定额管理,即确定一个合理的居民月用水量标准x(吨),月用水量不超过x的部分按平价收费,超出x的部分按议价收费.为了了解全市居民用水量的分布情况,通过抽样,获得了100位居民某年的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.
(1)求频率分布直方图中a的值.
(2)已知该市有80万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由.
(3)若该市政府希望使85%的居民每月的用水量不超过标准x(吨),估计x的值,并说明理由.
【解析】(1)由频率分布直方图,可得(0.08+0.16+a+0.40+0.52+a+0.12+0.08+0.04)×0.5=1,
解得a=0.30.
(2)用频率估计概率,由题可知80×0.5×(0.04+0.08+
0.12)=9.6,
所以全市居民中月均用水量不低于3吨的约为9.6万人.
(3)因为前6组的频率之和为(0.08+0.16+0.30+0.40+0.52+0.30)
×0.5=0.88>0.85,而前5组的频率之和为
(0.08+0.16+0.30+0.40+0.52)×0.5=0.73<0.85,所以2.5≤x<3.
由0.3×(x-2.5)=0.85-0.73,解得x=2.9.
因此,估计月用水量标准为2.9吨时,85%的居民每月的用水量不超过标准.
5.(文化自信)某动漫影视制作公司长期坚持文化自信,不断挖掘中华优秀传统文化中的动漫题材,创作出一批又一批的优秀动漫影视作品,获得市场和广大观众的一致好评,同时也为公司赢得丰厚的利润.该公司2013年至2019年的年利润y关于年份代号x的统计数据如表(已知该公司的年利润与年份代号线性相关):
年份
2013
2014
2015
2016
2017
2018
2019
年份代号x
1
2
3
4
5
6
7
年利润y
(单位:亿元)
29
33
36
44
48
52
59
(1)求y关于x的线性回归方程,并预测该公司2020年(年份代号记为8)的年利润;
(2)当统计表中某年年利润的实际值大于由(1)中线性回归方程计算出该年利润的估计值时,称该年为A级利润年,否则称为B级利润年.将(1)中预测的该公司2020年的年利润视作该年利润的实际值,现从2015年至2020年这6年中随机抽取2年,求恰有1年为A级利润年的概率.
【解析】(1)根据表中数据,计算可得
=4,
=43,
又
=28,
所以
因为
,所以
=43-5×4=23,
所以y关于x的线性回归方程为
=5x+23.
将x=8代入,得
=5×8+23=63.
所以该公司2020年的年利润的预测值为63亿元.
(2)由(1)可知2015年至2020年的年利润的估计值分别为38,43,48,53,58,63(单位:亿元),
其中实际利润大于相应估计值的有2年.
故这6年中,被评为A级利润年的有2年,分别记为A1,A2;
评为B级利润年的有4年,分别记为B1,B2,B3,B4,
从2015年至2020年中随机抽取2年,总的情况分别为:
A1A2,A1B1,A1B2,A1B3,A1B4,A2B1,A2B2,A2B3,A2B4,B1B2,B1B3,B1B4,B2B3,B2B4,B3B4,
共计15种情况.
其中恰有一年为A级利润年的情况分别为:A1B1,A1B2,A1B3,A1B4,A2B1,A2B2,A2B3,A2B4共有8种情况.
记“从2015年至2020年这6年的年利润中随机抽取2年,恰有一年为A级利润年”
的概率为P,故所求概率P=
.
6.(成绩分析)某校高一年级1
000名学生期中考试生物学科成绩的频率分布直方图如图所示,其中成绩分组情况如表:
组号
第一组
第二组
第三组
第四组
第五组
分组
[50,60)
[60,70)
[70,80)
[80,90)
[90,100]
(1)求生物成绩在[50,60)内的人数;
(2)若同组中的每个数据用该组区间中点值代替,根据频率分布直方图,估计这
1
000名学生生物成绩的平均分;
(3)现有5名同学,其中3人的成绩在第三组内,2人的成绩在第四组内,从这5名同学中随机抽取2名,求这2名同学来自不同组的概率.
【解析】(1)由题意,生物成绩在
内的频率为
1-(0.01×10+0.02×10+0.03×10+0.035×10)=0.05,
所以生物成绩在
内的人数为0.05×1
000=50.
(2)由频率分布直方图得,分数在[50,60)内的频率为0.05,[60,70)内的频率为
0.35,[70,80)内的频率为0.3,[80,90)内的频率为0.2,[90,100]内的频率为0.1,
所以这1
000名学生期中考试生物成绩的平均分的估计值为:55×0.05+65×0.35+75×0.3+85×0.2+95×0.1=74.5.
(3)设“这2名同学来自不同组”为事件A,设第三组的3名同学为a,b,c,
第四组的2名同学为x,y,则样本空间为Ω={(a,b),(a,c),(a,x),(a,y),(b,c),(b,x),(b,y),(c,x),(c,y),(x,y)},
事件A={(a,x),(a,y),(b,x),(b,y),(c,x),(c,y)}.
所以P(A)=
同课章节目录
