探究新题型:数学文化试题课件(共28张PPT)2021届高考二轮考前复习数学文科
文档属性
| 名称 | 探究新题型:数学文化试题课件(共28张PPT)2021届高考二轮考前复习数学文科 |  | |
| 格式 | ppt | ||
| 文件大小 | 531.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-18 22:06:54 | ||
图片预览







文档简介
(共28张PPT)
探究新题型 数学文化试题
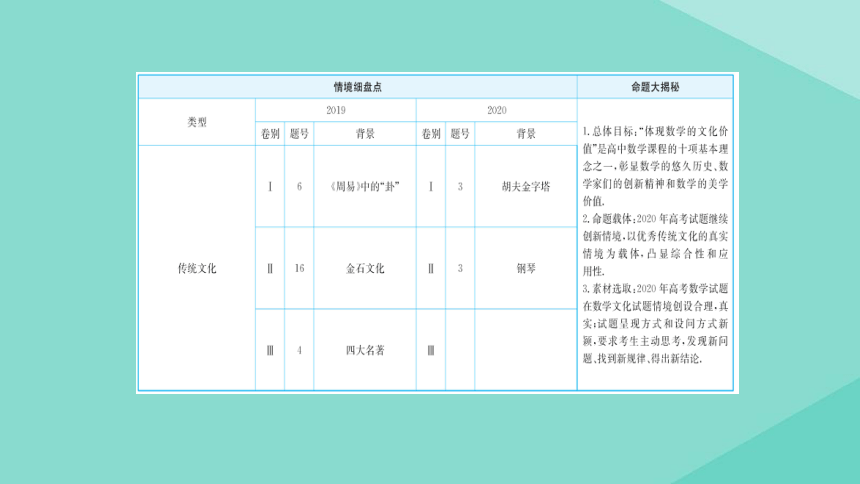
考向一 渗透中国传统文化
【典例1】(2020·全国Ⅱ卷)
北京天坛的圜丘坛为古代祭天的
场所,分上、中、下三层.上层中心有一块圆形石板(称为天心石),环绕天心石砌
9块扇面形石板构成第一环,向外每环依次增加9块,下一层的第一环比上一层的
最后一环多9块,向外每环依次也增加9块,已知每层环数相同,且下层比中层多
729块,则三层共有扇面形石板(不含天心石)
( )
A.3
699块
B.3
474块
C.
3
402块
D.3
339块
真题再研析·提升审题力
试题
情境
以北京天坛的圜丘坛的石板数为背景考查等差数列.
学科
应用
在中国传统文化的实际情境中从数学的视角发现问题,提出问题,分析问题,建立模型,计算求解,从而解决问题.
关键
能力
数学建模能力:运用提供的情境建立等差数列求和模型.
逻辑思维能力:通过对北京天坛的圜丘坛的石板数的数据收集、整理、分析,考查学生推理的能力.
运算求解能力:通过等差数列通项公式及前n项和的运算,考查数学运算的能力.
C 设每一层有n环,由题可知从内到外每环的扇面形石板数之间构成等差数
列{an},且公差d=9,首项a1=9,由等差数列的性质可知Sn,S2n-Sn,S3n-S2n成等差数
列,且(S3n-S2n)-(S2n-Sn)=n2d,由题意得9n2=729,
所以n=9,则三层共有扇面形石板为S3n=S27=27a1+
×9=3
402(块).
考向二 渗透外国文化
【典例2】(2020·全国Ⅰ卷)埃及胡夫金字塔是古代世界建筑奇迹之一,它的形
状可视为一个正四棱锥,以该四棱锥的高为边长的正方形面积等于该四棱锥一个
侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为
( )
A.
B.
C.
D.
试题
情境
以埃及胡夫金字塔为背景考查正四棱锥的有关概念及计算.
学科
应用
本题从数学角度对胡夫金字塔的问题进行解读.关注正四棱锥的有关概念及计算,体现了数学文化在数学中的应用.
关键
能力
数学运算能力:本题求解三角形底边上的高与底面正方形的边长的比,考查学生运算的能力.
数学建模能力:运用提供的情境建立正四棱锥的几何模型.
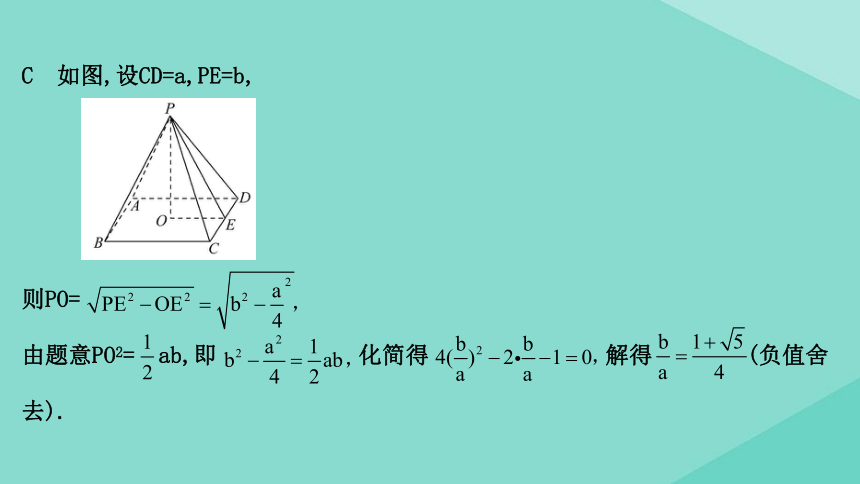
C 如图,设CD=a,PE=b,
则PO=
由题意PO2=
ab,即
化简得
解得
(负值舍
去).
1.(数学名家)朱世杰是历史上最伟大的数学家之一,他所著的
《四元玉鉴》卷中“如像招数”五问有如下问题:“今有官司
差夫一千八百六十四人筑堤.只云初日差六十四人,次日转多七人,每人日支米三
升,共支米四百三石九斗二升,问筑堤几日”.其大意为:“官府陆续派遣1
864人
前往修筑堤坝,第一天派出64人,从第二天开始,每天派出的人数比前一天多7人,
修筑堤坝的每人每天分发大米3升,共发出大米40
392升,问修筑堤坝多少天”.
这个问题中,前5天应发大米
( )
A.894升
B.1
170升
C.1
275米
D.1
467米
高考演兵场·检验考试力
B 因为第一天派出64人,从第二天开始,每天派出的人数比前一天多7人,所以第
5天派出:64+4×7=92人,所以前5天共派出S5=
=390(人),所以前5天应发大
米:390×3=1
170(升).
2.(九连环)九连环是中国杰出的益智游戏.九连环由九个相互连接的环组成,这
九个环套在一个中空的长形柄中,九连环的玩法就是要将这九个环从柄上解下来,
规则如下:如果要解下(或安上)第n环,则第(n-1)号环必须解下(或安上),n-1往
前的都要解下(或安上)才能实现.记解下n连环所需的最少移动步数为an,已知
a1=1,a2=2,an=an-1+2an-2+1(n≥3),则解六连环最少需要移动圆环步数为
( )
A.42
B.85
C.256
D.341
A 由题意可得:a3=a2+2a1+1=2+2+1=5,a4=a3+2a2+1=5+4+1=10,
a5=a4+2a3+1=10+10+1=21,a6=a5+2a4+1=21+20+1=42.
3.(数学名著)程大位《算法统宗》里有诗云“九百九十六斤棉,赠分八子做盘缠.
次第每人多十七,要将第八数来言.务要分明依次弟,孝和休惹外人传.”意
为:996斤棉花,分别赠送给8个子女做旅费,从第一个开始,以后每人依次多17斤,
直到第八个孩子为止.分配时一定要等级分明,使孝顺子女的美德外传,则第八个
孩子分得斤数为
( )
A.65
B.184
C.183
D.176
B 由题意可得,8个孩子所得的棉花构成公差为17的等差数列,且前8项和为996,
设首项为a1,结合等差数列前n项和公式有:S8=8a1+
d=8a1+28×17=996,解
得:a1=65,则a8=a1+7d=65+7×17=184.即第八个孩子分得斤数为184.
4.(牟合方盖)《九章算术》中,称一个正方体内两个互相垂直的内切圆柱所围成
的几何体为“牟合方盖”(如图).现提供一种计算“牟合方盖”体积的方法.显
然,正方体的内切球同时也是“牟合方盖”的内切球.因此,用任意平行于水平面
的平面去截“牟合方盖”,截面均为正方形,该平面截内切球得到的是上述正方
形截面的内切圆.结合祖暅原理,两个同高的立方体,如在等高处的截面积相等,
则体积相等;若正方体的棱长为2,则“牟合方盖”的体积为
( )
A.
B.2π
C.
D.
π
A 依题意,任意水平面与“牟合方盖”及其内切球相交的截面为正方形和一个
正方形的内切圆,正方形和内切圆的面积比为4∶π,由祖暅原理,“牟合方盖”
的体积和内切球的体积比为4∶π,又正方体的棱长为2,所以其内切球的半径为1,
所以内切球体积为
π,故“牟合方盖”的体积为
.
5.(中式园林)窗的运用是中式园林设计的重要组成部分,常常运用象征、隐喻、
借景等手法,将民族文化与哲理融入其中,营造出广阔的审美意境.从窗的外形看,
常见的有圆形、菱形、正六边形、正八边形等.如图,在平面直角坐标系xOy中,O
为正八边形P1P2…P8的中心,P1P8⊥x轴,现用如下方法等可能地确定点M:点M满足
2
=0(其中1≤i,j≤8,且i,j∈N
,i≠j),则点M(异于点O)落在坐标轴
上的概率为
( )
A.
B.
C.
D.
D 因为确定一个
需从8个向量
(1≤i≤8)中任取两个有
=28种取法,用
列举法得使点M(异于点O)落在坐标轴上的取法与
结合的有
,
两个,由于
每个向量都对应两个,但重复一次,所以共有
=8种,则点M落在坐标轴上的概率
为
=
.
6.(龙门石窟)河南洛阳的龙门石窟是中国石刻艺术宝库之一,现为世界文化遗产,
龙门石窟与莫高窟、云冈石窟、麦积山石窟并称中国四大石窟.现有一石窟的某
处“浮雕像”共7层,每上层的数量是下层的2倍,总共有1016个“浮雕像”,这些
“浮雕像”构成一幅优美的图案,若从最下层往上“浮雕像”的数量构成一个数
列{an},则log2
的值为
( )
A.8
B.10
C.12
D.16
C 因为最下层的“浮雕像”的数量为a1,依题有:公比q=2,n=7,S7=
=1
016,解得a1=8,则an=8×2n-1=2n+2
,所以a3=25,a5=27,从而
a3·a5=25×27=212,所以log2
=log2
=12.
7.(二十四节气)中国农历的“二十四节气”是凝结着中华民族的智慧与传统文
化的结晶,“二十四节气”歌是以“春、夏、秋、冬”开始的四句诗,2016年11
月30日,“二十四节气”正式被联合国教科文组织列入人类非物质文化遗产,也
被誉为“中国的第五大发明”.某小学三年级共有学生500名,随机抽查100名学
生并提问“二十四节气”歌,只能说出两句的有45人,能说出三句及其以上的有
32人,据此估计该校三年级的500名学生中,对“二十四节气”歌只能说出一句或
一句也说不出的大约有
( )
A.69人
84人
C.108人
D.115人
D 由题意,100人中只能说出一句或一句也说不出的同学有100-45-32=23人,故
只能说出一句或一句也说不出的学生占的比例为
,故只能说出一句或一句也
说不出的学生共有500×
=115人.
8.(中古玉器)玉琮是中国古代玉器中重要的礼器,神人纹玉
琮王是新石器时代良渚文化的典型玉器,1986年出土于浙江
省余杭市反山文化遗址.玉琮王通高8.8
cm,孔径4.9
cm,外
径17.6
cm.琮体四面各琢刻一完整的兽面神人图.兽面的两侧各浅浮雕鸟纹.器
形呈扁矮的方柱体,内圆外方,上下端为圆面的射,中心有一上下垂直相透的圆孔.
试估计该神人纹玉琮王的体积约为(单位:cm3)
( )
A.6
250
B.3
050
C.2
850
D.2
350
D 由题可知,该神人纹玉琮王可看成是一个底面边长为17.6
cm,高为8.8
cm的
正四棱柱中挖去一个底面直径为4.9
cm,高为8.8
cm的圆柱,此时求得体积记为
V1,V1=
×8.8-π×
×8.8≈2560(cm3),
记该神人纹玉琮王的实际体积为V,则Vπ×
×8.8-
π×
×8.8≈1
975(cm3),故1
975560.
9.(良渚古城遗址)中国良渚古城遗址获准列入世界遗产名录,标志着中华五千年
文明史得到国际社会认可.良渚古城遗址是人类早期城市文明的范例,证实了中
华五千年文明史.考古科学家在测定遗址年龄的过程中利用了“放射性物质因衰
变而减少”这一规律.已知样本中碳14的质量N随时间t(单位:年)的衰变规律满
足N=N0·
(N0表示碳14原有的质量),则经过5
730年后,碳14的质量变为原来
的________;经过测定,良渚古城遗址文物样本中碳14的质量是原来的
至
,
据此推测良渚古城存在的时期距今约在________年到5
730年之间.(参考数
据:log23≈1.6,log25≈2.3)?
【解析】因为文物样本中碳14的质量N与时间t之间的函数关系式为:
N=N0·
;
t=5
730时,N=N0·2-1=
;
所以每经过5
730年衰减为原来的
;
由于良渚古城遗址文物样本中碳14的质量是原来的
至
,所以
≤
≤
;
两边同时取以2为底的对数,得:-1≤-
≤(log23-log25)=-0.7.
所以4
011≤t≤5
730;
故推测良渚古城存在的时期距今约在4
011年到5
730年之间.
答案:
4
011
10.(进位制)国际数学教育大会(ICME)是世界数学教育规模最大、水平最高的学
术性会议,第十四届大会将在上海召开,其会标如图,包含着许多数学元素.主画
面是非常优美的几何化的中心对称图形,由弦图、圆和螺线组成,主画面标明的
ICME-14下方的“? ? ? ?”是用中国古代八进制的计数符号写出的八进
制数3
744,也可以读出其二进制码11111100100,换算成十进制的数是n,则
=______.?
【解析】由题意将八进制数3
744换算成十进制的数得:4×80+4×81+7×82+3×83=2
020,
所以
答案:-1
探究新题型 数学文化试题
考向一 渗透中国传统文化
【典例1】(2020·全国Ⅱ卷)
北京天坛的圜丘坛为古代祭天的
场所,分上、中、下三层.上层中心有一块圆形石板(称为天心石),环绕天心石砌
9块扇面形石板构成第一环,向外每环依次增加9块,下一层的第一环比上一层的
最后一环多9块,向外每环依次也增加9块,已知每层环数相同,且下层比中层多
729块,则三层共有扇面形石板(不含天心石)
( )
A.3
699块
B.3
474块
C.
3
402块
D.3
339块
真题再研析·提升审题力
试题
情境
以北京天坛的圜丘坛的石板数为背景考查等差数列.
学科
应用
在中国传统文化的实际情境中从数学的视角发现问题,提出问题,分析问题,建立模型,计算求解,从而解决问题.
关键
能力
数学建模能力:运用提供的情境建立等差数列求和模型.
逻辑思维能力:通过对北京天坛的圜丘坛的石板数的数据收集、整理、分析,考查学生推理的能力.
运算求解能力:通过等差数列通项公式及前n项和的运算,考查数学运算的能力.
C 设每一层有n环,由题可知从内到外每环的扇面形石板数之间构成等差数
列{an},且公差d=9,首项a1=9,由等差数列的性质可知Sn,S2n-Sn,S3n-S2n成等差数
列,且(S3n-S2n)-(S2n-Sn)=n2d,由题意得9n2=729,
所以n=9,则三层共有扇面形石板为S3n=S27=27a1+
×9=3
402(块).
考向二 渗透外国文化
【典例2】(2020·全国Ⅰ卷)埃及胡夫金字塔是古代世界建筑奇迹之一,它的形
状可视为一个正四棱锥,以该四棱锥的高为边长的正方形面积等于该四棱锥一个
侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为
( )
A.
B.
C.
D.
试题
情境
以埃及胡夫金字塔为背景考查正四棱锥的有关概念及计算.
学科
应用
本题从数学角度对胡夫金字塔的问题进行解读.关注正四棱锥的有关概念及计算,体现了数学文化在数学中的应用.
关键
能力
数学运算能力:本题求解三角形底边上的高与底面正方形的边长的比,考查学生运算的能力.
数学建模能力:运用提供的情境建立正四棱锥的几何模型.
C 如图,设CD=a,PE=b,
则PO=
由题意PO2=
ab,即
化简得
解得
(负值舍
去).
1.(数学名家)朱世杰是历史上最伟大的数学家之一,他所著的
《四元玉鉴》卷中“如像招数”五问有如下问题:“今有官司
差夫一千八百六十四人筑堤.只云初日差六十四人,次日转多七人,每人日支米三
升,共支米四百三石九斗二升,问筑堤几日”.其大意为:“官府陆续派遣1
864人
前往修筑堤坝,第一天派出64人,从第二天开始,每天派出的人数比前一天多7人,
修筑堤坝的每人每天分发大米3升,共发出大米40
392升,问修筑堤坝多少天”.
这个问题中,前5天应发大米
( )
A.894升
B.1
170升
C.1
275米
D.1
467米
高考演兵场·检验考试力
B 因为第一天派出64人,从第二天开始,每天派出的人数比前一天多7人,所以第
5天派出:64+4×7=92人,所以前5天共派出S5=
=390(人),所以前5天应发大
米:390×3=1
170(升).
2.(九连环)九连环是中国杰出的益智游戏.九连环由九个相互连接的环组成,这
九个环套在一个中空的长形柄中,九连环的玩法就是要将这九个环从柄上解下来,
规则如下:如果要解下(或安上)第n环,则第(n-1)号环必须解下(或安上),n-1往
前的都要解下(或安上)才能实现.记解下n连环所需的最少移动步数为an,已知
a1=1,a2=2,an=an-1+2an-2+1(n≥3),则解六连环最少需要移动圆环步数为
( )
A.42
B.85
C.256
D.341
A 由题意可得:a3=a2+2a1+1=2+2+1=5,a4=a3+2a2+1=5+4+1=10,
a5=a4+2a3+1=10+10+1=21,a6=a5+2a4+1=21+20+1=42.
3.(数学名著)程大位《算法统宗》里有诗云“九百九十六斤棉,赠分八子做盘缠.
次第每人多十七,要将第八数来言.务要分明依次弟,孝和休惹外人传.”意
为:996斤棉花,分别赠送给8个子女做旅费,从第一个开始,以后每人依次多17斤,
直到第八个孩子为止.分配时一定要等级分明,使孝顺子女的美德外传,则第八个
孩子分得斤数为
( )
A.65
B.184
C.183
D.176
B 由题意可得,8个孩子所得的棉花构成公差为17的等差数列,且前8项和为996,
设首项为a1,结合等差数列前n项和公式有:S8=8a1+
d=8a1+28×17=996,解
得:a1=65,则a8=a1+7d=65+7×17=184.即第八个孩子分得斤数为184.
4.(牟合方盖)《九章算术》中,称一个正方体内两个互相垂直的内切圆柱所围成
的几何体为“牟合方盖”(如图).现提供一种计算“牟合方盖”体积的方法.显
然,正方体的内切球同时也是“牟合方盖”的内切球.因此,用任意平行于水平面
的平面去截“牟合方盖”,截面均为正方形,该平面截内切球得到的是上述正方
形截面的内切圆.结合祖暅原理,两个同高的立方体,如在等高处的截面积相等,
则体积相等;若正方体的棱长为2,则“牟合方盖”的体积为
( )
A.
B.2π
C.
D.
π
A 依题意,任意水平面与“牟合方盖”及其内切球相交的截面为正方形和一个
正方形的内切圆,正方形和内切圆的面积比为4∶π,由祖暅原理,“牟合方盖”
的体积和内切球的体积比为4∶π,又正方体的棱长为2,所以其内切球的半径为1,
所以内切球体积为
π,故“牟合方盖”的体积为
.
5.(中式园林)窗的运用是中式园林设计的重要组成部分,常常运用象征、隐喻、
借景等手法,将民族文化与哲理融入其中,营造出广阔的审美意境.从窗的外形看,
常见的有圆形、菱形、正六边形、正八边形等.如图,在平面直角坐标系xOy中,O
为正八边形P1P2…P8的中心,P1P8⊥x轴,现用如下方法等可能地确定点M:点M满足
2
=0(其中1≤i,j≤8,且i,j∈N
,i≠j),则点M(异于点O)落在坐标轴
上的概率为
( )
A.
B.
C.
D.
D 因为确定一个
需从8个向量
(1≤i≤8)中任取两个有
=28种取法,用
列举法得使点M(异于点O)落在坐标轴上的取法与
结合的有
,
两个,由于
每个向量都对应两个,但重复一次,所以共有
=8种,则点M落在坐标轴上的概率
为
=
.
6.(龙门石窟)河南洛阳的龙门石窟是中国石刻艺术宝库之一,现为世界文化遗产,
龙门石窟与莫高窟、云冈石窟、麦积山石窟并称中国四大石窟.现有一石窟的某
处“浮雕像”共7层,每上层的数量是下层的2倍,总共有1016个“浮雕像”,这些
“浮雕像”构成一幅优美的图案,若从最下层往上“浮雕像”的数量构成一个数
列{an},则log2
的值为
( )
A.8
B.10
C.12
D.16
C 因为最下层的“浮雕像”的数量为a1,依题有:公比q=2,n=7,S7=
=1
016,解得a1=8,则an=8×2n-1=2n+2
,所以a3=25,a5=27,从而
a3·a5=25×27=212,所以log2
=log2
=12.
7.(二十四节气)中国农历的“二十四节气”是凝结着中华民族的智慧与传统文
化的结晶,“二十四节气”歌是以“春、夏、秋、冬”开始的四句诗,2016年11
月30日,“二十四节气”正式被联合国教科文组织列入人类非物质文化遗产,也
被誉为“中国的第五大发明”.某小学三年级共有学生500名,随机抽查100名学
生并提问“二十四节气”歌,只能说出两句的有45人,能说出三句及其以上的有
32人,据此估计该校三年级的500名学生中,对“二十四节气”歌只能说出一句或
一句也说不出的大约有
( )
A.69人
84人
C.108人
D.115人
D 由题意,100人中只能说出一句或一句也说不出的同学有100-45-32=23人,故
只能说出一句或一句也说不出的学生占的比例为
,故只能说出一句或一句也
说不出的学生共有500×
=115人.
8.(中古玉器)玉琮是中国古代玉器中重要的礼器,神人纹玉
琮王是新石器时代良渚文化的典型玉器,1986年出土于浙江
省余杭市反山文化遗址.玉琮王通高8.8
cm,孔径4.9
cm,外
径17.6
cm.琮体四面各琢刻一完整的兽面神人图.兽面的两侧各浅浮雕鸟纹.器
形呈扁矮的方柱体,内圆外方,上下端为圆面的射,中心有一上下垂直相透的圆孔.
试估计该神人纹玉琮王的体积约为(单位:cm3)
( )
A.6
250
B.3
050
C.2
850
D.2
350
D 由题可知,该神人纹玉琮王可看成是一个底面边长为17.6
cm,高为8.8
cm的
正四棱柱中挖去一个底面直径为4.9
cm,高为8.8
cm的圆柱,此时求得体积记为
V1,V1=
×8.8-π×
×8.8≈2560(cm3),
记该神人纹玉琮王的实际体积为V,则V
×8.8-
π×
×8.8≈1
975(cm3),故1
975
9.(良渚古城遗址)中国良渚古城遗址获准列入世界遗产名录,标志着中华五千年
文明史得到国际社会认可.良渚古城遗址是人类早期城市文明的范例,证实了中
华五千年文明史.考古科学家在测定遗址年龄的过程中利用了“放射性物质因衰
变而减少”这一规律.已知样本中碳14的质量N随时间t(单位:年)的衰变规律满
足N=N0·
(N0表示碳14原有的质量),则经过5
730年后,碳14的质量变为原来
的________;经过测定,良渚古城遗址文物样本中碳14的质量是原来的
至
,
据此推测良渚古城存在的时期距今约在________年到5
730年之间.(参考数
据:log23≈1.6,log25≈2.3)?
【解析】因为文物样本中碳14的质量N与时间t之间的函数关系式为:
N=N0·
;
t=5
730时,N=N0·2-1=
;
所以每经过5
730年衰减为原来的
;
由于良渚古城遗址文物样本中碳14的质量是原来的
至
,所以
≤
≤
;
两边同时取以2为底的对数,得:-1≤-
≤(log23-log25)=-0.7.
所以4
011≤t≤5
730;
故推测良渚古城存在的时期距今约在4
011年到5
730年之间.
答案:
4
011
10.(进位制)国际数学教育大会(ICME)是世界数学教育规模最大、水平最高的学
术性会议,第十四届大会将在上海召开,其会标如图,包含着许多数学元素.主画
面是非常优美的几何化的中心对称图形,由弦图、圆和螺线组成,主画面标明的
ICME-14下方的“? ? ? ?”是用中国古代八进制的计数符号写出的八进
制数3
744,也可以读出其二进制码11111100100,换算成十进制的数是n,则
=______.?
【解析】由题意将八进制数3
744换算成十进制的数得:4×80+4×81+7×82+3×83=2
020,
所以
答案:-1
同课章节目录
