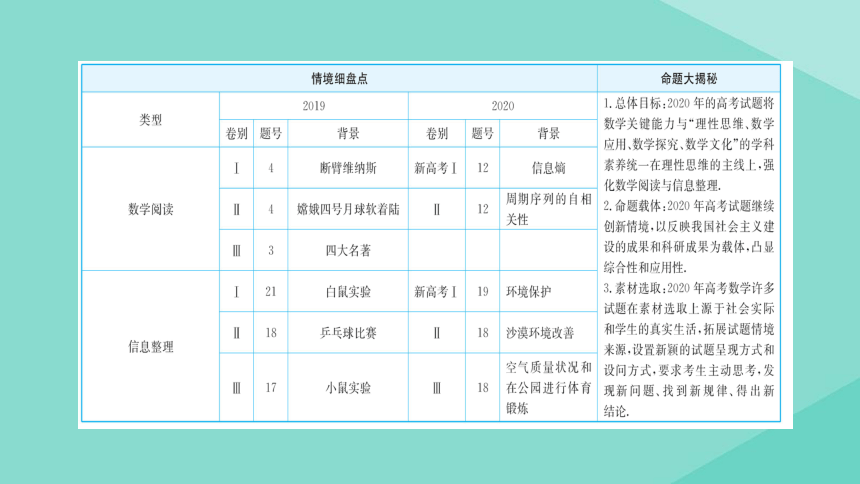
探究新题型:数学阅读与信息整理课件(共31张PPT)2021届高考二轮考前复习数学文科
文档属性
| 名称 | 探究新题型:数学阅读与信息整理课件(共31张PPT)2021届高考二轮考前复习数学文科 |  | |
| 格式 | ppt | ||
| 文件大小 | 935.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-19 22:07:22 | ||
图片预览




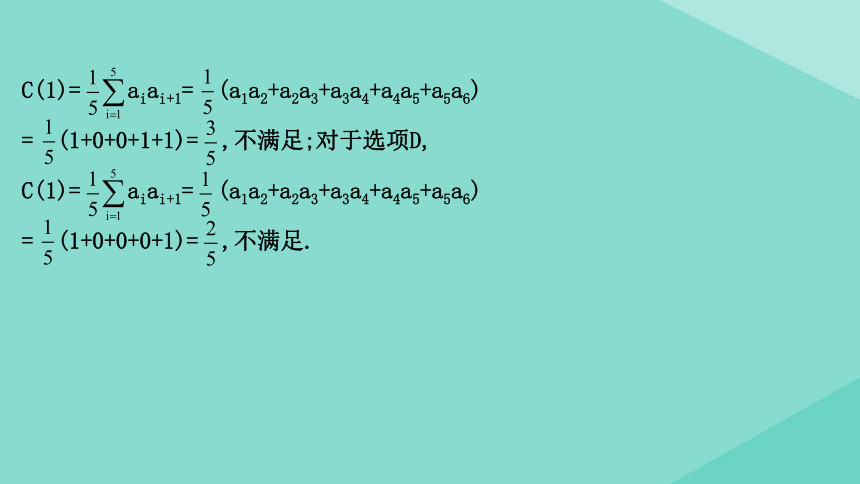






文档简介
(共31张PPT)
探究新题型 数学阅读与信息整理
考向一 数学阅读
【典例1】(2020·全国Ⅱ卷)0-1周期序列在通信技术中有着重
要应用.若序列a1a2…an…满足ai∈{0,1}(i=1,2,…),且存在正整数m,使得
ai+m=ai(i=1,2,…)成立,则称其为0-1周期序列,并称满足ai+m=ai(i=1,2,…)的最
小正整数m为这个序列的周期.对于周期为m的0-1序列a1a2…an…,C(k)=
(k=1,2,…,m-1)是描述其性质的重要指标,下列周期为5的0-1序列中,
满足C(k)≤
(k=1,2,3,4)的序列是
( )
A.11010…
B.11011…
C.10001…
D.11001…
真题再研析·提升审题力
试题
情境
以周期序列的自相关性为背景,要求判断试题给出的四个周期序列是否满足题设条件.
学科
应用
主要考查学生对新概念的理解、探究能力.考查学生数学阅读的能力,对培养学生的创新应用意识起到积极引导作用.
关键
能力
逻辑思维能力:通过对周期序列的自相关性数据收集、整理、分析,考查学生逻辑推理能力.
运算求解能力:通过分类求解序列号,考查学生数学运算能力.
C 由ai+m=ai知,序列ai的周期为m,由已知,m=5,
C(k)=
aiai+k(k=1,2,3,4),对于选项A,
C(1)=
aiai+1=
(a1a2+a2a3+a3a4+a4a5+a5a6)
=
(1+0+0+0+0)=
≤
,
C(2)=
aiai+2=
(a1a3+a2a4+a3a5+a4a6+a5a7)
=
(0+1+0+1+0)=
,不满足;对于选项B,
C(1)=
aiai+1=
(a1a2+a2a3+a3a4+a4a5+a5a6)
=
(1+0+0+1+1)=
,不满足;对于选项D,
C(1)=
aiai+1=
(a1a2+a2a3+a3a4+a4a5+a5a6)
=
(1+0+0+0+1)=
,不满足.
考向二 信息整理
【典例2】(2020·全国Ⅱ卷)某沙漠地区经过治理,生态系统得到很大改善,野生
动物数量有所增加.为调查该地区某种野生动物的数量,将其分成面积相近的200
个地块,从这些地块中用简单随机抽样的方法抽取20个作为样区,调查得到样本
数据(xi,yi)(i=1,2,…,20),其中xi和yi分别表示第i个样区的植物覆盖面积(单
位:公顷)和这种野生动物的数量,并计算得
xi=60,
yi=1
200,
(xi-
)2=80,
(yi-
)2=9
000,
(xi-
)(yi-
)=800.
(1)求该地区这种野生动物数量的估计值(这种野生动物数量的估计值等于样区
这种野生动物数量的平均数乘以地块数);
(2)求样本(xi,yi)(i=1,2,…,20)的相关系数(精确到0.01);
(3)根据现有统计资料,各地块间植物覆盖面积差异很大.为提高样本的代表性以
获得该地区这种野生动物数量更准确的估计,请给出一种你认为更合理的抽样方
法,并说明理由.
附:相关系数r=
试题
情境
以沙漠治理为背景设计,考查学生分析和解决问题的能力、数据处理的能力,以及应用数学模型分析解决实际问题的能力.
学科
应用
试题通过建立数学模型,考查学生整理和分析信息的能力.
关键
能力
数学建模能力:重点考查学生对概率统计基本思想、基本统计模型的理解和运用.
运算求解能力:本题设置了对动物数量的估计值、相关系数的求解,重在考查学生运算求解的能力.
逻辑思维能力:根据对野生动物数量更准确的估计,确定合理的抽样方案,培养学生逻辑推理能力.
【解析】(1)样区这种野生动物数量的平均数为
=
×1
200=60,
地块数为200,该地区这种野生动物数量的估计值为200×60=12
000.
(2)样本(xi,yi)的相关系数
r=
=
≈0.94.
(3)分层抽样:根据植物覆盖面积的大小对地块分层,再对200个地块进行分层抽
样.
理由如下:由(2)知各地块的这种野生动物数量与植物覆盖面积有很强的正相关.由于各地块间植物覆盖面积差异很大,从而各地块间这种野生动物数量差异也很大,采用分层抽样的办法较好地保持了样本结构与总体结构的一致性,提高了样本代表性,从而可以获得该地区这种野生动物数量更准确的估计.
【数学阅读】
1.(螺旋蚊香)原始的蚊香出现在宋代.根据宋代冒苏轼之名编写
的《格物粗谈》记载:“端午时,收贮浮萍,阴干,加雄黄,
作纸缠香,烧之,能祛蚊虫.”如图,为某校数学兴趣小组用
数学软件制作的“螺旋蚊香”,画法如下:在水平直线l上
取长度为1的线段AB,作一个等边三角形ABC,然后以点B为
圆心,AB为半径逆时针画圆弧,交线段CB的延长线于点D,再以点C为圆心,CD为半
径逆时针画圆弧,交线段AC的延长线于点E,以此类推,当得到的“螺旋蚊香”与
直线l恰有21个交点时,“螺旋蚊香”的总长度的最小值为
( )
A.310π
B.340π
C.930π
D.1
020π
高考演兵场·检验考试力
A 当以B为圆心,半径为:1,4,7,10,…①
当以C为圆心,半径为:2,5,8,11,…②
当以A为圆心,半径为:3,6,9,12,…③
所以当“螺旋蚊香”与直线l恰有21个交点时,若使“螺旋蚊香”的总长度最小,
则完成整数个循环,所以以B为圆心的弧与直线只有交点A(其余的与以A为圆心的
弧与直线交点重合),以C为圆心的弧与直线10个交点,以A为圆心的弧与直线有10
个交点,即数列②有10项,数列③有10项,
所以最后一个圆弧的半径为r=3+3(10-1)=30,
所以“螺旋蚊香”的总长度的最小值为l=
×2π×
=
=310π.
2.(5G技术)中国的5G技术领先世界,5G技术的数学原理之一便是著名的香农公
式:C=Wlog2
.它表示:在受噪声干扰的信道中,最大信息传递速度C取决于
信道带宽W,信道内信号的平均功率S,信道内部的高斯噪声功率N的大小,其中
叫做信噪比.当信噪比比较大时,公式中真数中的1可以忽略不计.按照香农公式,
若不改变带宽W,而将信噪比
从1
000提升至4
000,则C大约增加了
( )
附:lg
2≈0.301
0
A.10%
B.20%
C.50%
D.100%
B 当
=1
000时,C≈Wlog21
000,当
=4
000时,C≈Wlog24
000,因为
,
所以将信噪比
从1
000提升至4
000,则C大约增加了20%.
3.(病毒学)1943年,我国病毒学家黄祯祥在美国发表了对病毒学研究有重大影响
的论文“西方马脑炎病毒在组织培养上滴定和中和作用的进一步研究”,这一研
究成果,使病毒在试管内繁殖成为现实,从此摆脱了人工繁殖病毒靠动物、鸡胚
培养的原始落后的方法.若试管内某种病毒细胞的总数y和天数t的函数关系
为:y=2t-1,且该种病毒细胞的个数超过108时会发生变异,则该种病毒细胞实验最
多进行的天数为
( )
(lg
2≈0.301
0)
A.25
B.26
C.27
D.28
C 令y=2t-1=108,故t-1=log2108=8log210,
即t=8log210+1=8
+1≈27.6,
故该种病毒细胞实验最多进行的天数为27.
4.(旅游纪念)甲乙丙丁四位同学一起到某地旅游,当地有A,B,C,D,E,F六种手工纪念品,他们打算每人买一种,甲说:只要不是A就行;乙说:C,D,E,F都行;丙说:我喜欢C,但是只要不是D就行;丁说:除了C,E之外,其他的都可以.据此判断,他们四人可以共同买的手工纪念品为________.?
【解析】甲可以选择的手工纪念品的集合为:{B,C,D,E,F},乙可以选择的手工纪念品的集合为{C,D,E,F},丙可以选择的手工纪念品的集合为{A,B,C,E,F},丁可以选择的手工纪念品的集合为{A,B,D,F},这四个集合的交集中只有元素F,故答案为F.
答案:F
【信息整理】
5.(信息安全)为了保证信息的安全传输,有一种为秘密密钥密码系统,其加密、解密原理为:发送方由明文到密文(加密),接收方由密文到明文(解密).现在加密密钥为y=xα(α为常数),如“4”通过加密后得到密文“2”.若接收方接到密文“3”,则解密后得到的明文
( )
A.4
B.6
C.8
D.9
D 由题目可知加密密钥y=xα(α是常数)是一个幂函数模型,所以要想求得解密
后得到的明文,就必须先求出α的值.由题意得2=4α,解得α=
,则y=
,由
=3,得x=9.
6.(瓷器)中国是世界上最古老的文明中心之一,中国古代对世界上最重要的贡献
之一就是发明了瓷器,中国陶瓷是世界上独一无二的.它的发展过程蕴藏着十分
丰富的科学和艺术,陶瓷形状各式各样,从不同角度诠释了数学中几何的形式之
美.现有一椭圆形明代瓷盘,经测量得到图中数据,则该椭圆瓷盘的焦距为
( )
A.8
cm
B.2
cm
C.4
cm
D.4
cm
C 根据椭圆的定义,得到:2a=8,解得a=4,2b=4,解得b=2,
所以c=
,所以焦距2c=4
(cm).
7.(粒子运动)如图,一个粒子从原点出发,在第一象限和两坐标轴
正半轴上运动,在第一秒时它从原点运动到点(0,1),接着它按图
所示在y轴、x轴的垂直方向上来回运动,且每秒移动一个单位长
度,那么,在2
018秒时,这个粒子所处的位置在点________.?
【解析】如图,设粒子运动到A1,A2,…,An时所用的时间分别为a1,a2,…,an,
则a1=2,a2=6,a3=12,a4=20,…,an-an-1=2n,
将a2-a1=2×2,a3-a2=2×3,a4-a3=2×4,…,an-an-1=2n相加得:
an-a1=2(2+3+4+…+n)=n2+n-2,则an=n(n+1),由44×45=1
980,故运动了1
980秒
时它到点A44(44,44),
又由运动规律知:A1,A2,…,An中,奇数点处向下运动,偶数点处向左运动,故粒子
到达A44(44,44)时向左运动38秒,即运动了2
018秒到达点(6,44),则所求点应为
(6,44).
答案:(6,44).
8.(学习强国)“学习强国”学习平台是由中宣部主管,以深入学习宣传习近平新
时代中国特色社会主义思想为主要内容,立足全体党员,面向全社会的优质平台,
现日益成为老百姓了解国家动态,紧跟时代脉博的热门APP,某市宣传部门为了解
全民利用“学习强国”了解国家动态的情况,从全市抽取2
000名人员进行调查,
统计他们每周利用“学习强国”的时长,如图是根据调查结果绘制的频率分布直
方图.
(1)根据频率分布直方图,求所有被抽查人员利用“学习强国”的平均时长和中
位数;
(2)宣传部为了了解大家利用“学习强国”的具体情况,准备采用分层抽样的方
法从[8,10)和[10,12)组中抽取50人了解情况,则两组各抽取多少人?再利用分层
抽样从抽取的50人中选5人参加一个座谈会.现从参加座谈会的5人中随机抽取两
人发言,求[10,12)组中至少有1人发言的概率.
【解析】(1)设被抽查人员利用“学习强国”的平均时长为
,中位数为y,
=0.05×1+0.1×3+0.25×5+0.3×7+0.15×9+0.1×11+0.05×13=6.8,0.05+
0.1+0.25+0.15×(y-6)=0.5,解得y=
,即被抽查人员利用“学习强国”的平均
时长为6.8,中位数为
.
(2)[8,10)组的人数为2
000×0.15=300,
设抽取的人数为a,[10,12)组的人数为2
000×0.1=200,设抽取的人数为b,
则
=
=
,解得a=30,b=20,
所以在[8,10)和[10,12)两组中分别抽取30人和20人,再抽取5人,两组分别抽取
3人和2人,将[8,10)组中被抽取的工作人员标记为A1,A2,A3,将[10,12)中的标记
为B1,B2.
设事件C表示从[10,12)组中至少抽取1人,
则抽取的情况如下:{A1,A2},{A1,A3},{A1,B1},{A1,B2},{A2,A3},{A2,B1},{A2,B2},{A3,B1},{A3,B2},
{B1,B2},共10种情况,
其中在[10,12)组中至少抽取1人的情况有7种,则
P(C)=
.
探究新题型 数学阅读与信息整理
考向一 数学阅读
【典例1】(2020·全国Ⅱ卷)0-1周期序列在通信技术中有着重
要应用.若序列a1a2…an…满足ai∈{0,1}(i=1,2,…),且存在正整数m,使得
ai+m=ai(i=1,2,…)成立,则称其为0-1周期序列,并称满足ai+m=ai(i=1,2,…)的最
小正整数m为这个序列的周期.对于周期为m的0-1序列a1a2…an…,C(k)=
(k=1,2,…,m-1)是描述其性质的重要指标,下列周期为5的0-1序列中,
满足C(k)≤
(k=1,2,3,4)的序列是
( )
A.11010…
B.11011…
C.10001…
D.11001…
真题再研析·提升审题力
试题
情境
以周期序列的自相关性为背景,要求判断试题给出的四个周期序列是否满足题设条件.
学科
应用
主要考查学生对新概念的理解、探究能力.考查学生数学阅读的能力,对培养学生的创新应用意识起到积极引导作用.
关键
能力
逻辑思维能力:通过对周期序列的自相关性数据收集、整理、分析,考查学生逻辑推理能力.
运算求解能力:通过分类求解序列号,考查学生数学运算能力.
C 由ai+m=ai知,序列ai的周期为m,由已知,m=5,
C(k)=
aiai+k(k=1,2,3,4),对于选项A,
C(1)=
aiai+1=
(a1a2+a2a3+a3a4+a4a5+a5a6)
=
(1+0+0+0+0)=
≤
,
C(2)=
aiai+2=
(a1a3+a2a4+a3a5+a4a6+a5a7)
=
(0+1+0+1+0)=
,不满足;对于选项B,
C(1)=
aiai+1=
(a1a2+a2a3+a3a4+a4a5+a5a6)
=
(1+0+0+1+1)=
,不满足;对于选项D,
C(1)=
aiai+1=
(a1a2+a2a3+a3a4+a4a5+a5a6)
=
(1+0+0+0+1)=
,不满足.
考向二 信息整理
【典例2】(2020·全国Ⅱ卷)某沙漠地区经过治理,生态系统得到很大改善,野生
动物数量有所增加.为调查该地区某种野生动物的数量,将其分成面积相近的200
个地块,从这些地块中用简单随机抽样的方法抽取20个作为样区,调查得到样本
数据(xi,yi)(i=1,2,…,20),其中xi和yi分别表示第i个样区的植物覆盖面积(单
位:公顷)和这种野生动物的数量,并计算得
xi=60,
yi=1
200,
(xi-
)2=80,
(yi-
)2=9
000,
(xi-
)(yi-
)=800.
(1)求该地区这种野生动物数量的估计值(这种野生动物数量的估计值等于样区
这种野生动物数量的平均数乘以地块数);
(2)求样本(xi,yi)(i=1,2,…,20)的相关系数(精确到0.01);
(3)根据现有统计资料,各地块间植物覆盖面积差异很大.为提高样本的代表性以
获得该地区这种野生动物数量更准确的估计,请给出一种你认为更合理的抽样方
法,并说明理由.
附:相关系数r=
试题
情境
以沙漠治理为背景设计,考查学生分析和解决问题的能力、数据处理的能力,以及应用数学模型分析解决实际问题的能力.
学科
应用
试题通过建立数学模型,考查学生整理和分析信息的能力.
关键
能力
数学建模能力:重点考查学生对概率统计基本思想、基本统计模型的理解和运用.
运算求解能力:本题设置了对动物数量的估计值、相关系数的求解,重在考查学生运算求解的能力.
逻辑思维能力:根据对野生动物数量更准确的估计,确定合理的抽样方案,培养学生逻辑推理能力.
【解析】(1)样区这种野生动物数量的平均数为
=
×1
200=60,
地块数为200,该地区这种野生动物数量的估计值为200×60=12
000.
(2)样本(xi,yi)的相关系数
r=
=
≈0.94.
(3)分层抽样:根据植物覆盖面积的大小对地块分层,再对200个地块进行分层抽
样.
理由如下:由(2)知各地块的这种野生动物数量与植物覆盖面积有很强的正相关.由于各地块间植物覆盖面积差异很大,从而各地块间这种野生动物数量差异也很大,采用分层抽样的办法较好地保持了样本结构与总体结构的一致性,提高了样本代表性,从而可以获得该地区这种野生动物数量更准确的估计.
【数学阅读】
1.(螺旋蚊香)原始的蚊香出现在宋代.根据宋代冒苏轼之名编写
的《格物粗谈》记载:“端午时,收贮浮萍,阴干,加雄黄,
作纸缠香,烧之,能祛蚊虫.”如图,为某校数学兴趣小组用
数学软件制作的“螺旋蚊香”,画法如下:在水平直线l上
取长度为1的线段AB,作一个等边三角形ABC,然后以点B为
圆心,AB为半径逆时针画圆弧,交线段CB的延长线于点D,再以点C为圆心,CD为半
径逆时针画圆弧,交线段AC的延长线于点E,以此类推,当得到的“螺旋蚊香”与
直线l恰有21个交点时,“螺旋蚊香”的总长度的最小值为
( )
A.310π
B.340π
C.930π
D.1
020π
高考演兵场·检验考试力
A 当以B为圆心,半径为:1,4,7,10,…①
当以C为圆心,半径为:2,5,8,11,…②
当以A为圆心,半径为:3,6,9,12,…③
所以当“螺旋蚊香”与直线l恰有21个交点时,若使“螺旋蚊香”的总长度最小,
则完成整数个循环,所以以B为圆心的弧与直线只有交点A(其余的与以A为圆心的
弧与直线交点重合),以C为圆心的弧与直线10个交点,以A为圆心的弧与直线有10
个交点,即数列②有10项,数列③有10项,
所以最后一个圆弧的半径为r=3+3(10-1)=30,
所以“螺旋蚊香”的总长度的最小值为l=
×2π×
=
=310π.
2.(5G技术)中国的5G技术领先世界,5G技术的数学原理之一便是著名的香农公
式:C=Wlog2
.它表示:在受噪声干扰的信道中,最大信息传递速度C取决于
信道带宽W,信道内信号的平均功率S,信道内部的高斯噪声功率N的大小,其中
叫做信噪比.当信噪比比较大时,公式中真数中的1可以忽略不计.按照香农公式,
若不改变带宽W,而将信噪比
从1
000提升至4
000,则C大约增加了
( )
附:lg
2≈0.301
0
A.10%
B.20%
C.50%
D.100%
B 当
=1
000时,C≈Wlog21
000,当
=4
000时,C≈Wlog24
000,因为
,
所以将信噪比
从1
000提升至4
000,则C大约增加了20%.
3.(病毒学)1943年,我国病毒学家黄祯祥在美国发表了对病毒学研究有重大影响
的论文“西方马脑炎病毒在组织培养上滴定和中和作用的进一步研究”,这一研
究成果,使病毒在试管内繁殖成为现实,从此摆脱了人工繁殖病毒靠动物、鸡胚
培养的原始落后的方法.若试管内某种病毒细胞的总数y和天数t的函数关系
为:y=2t-1,且该种病毒细胞的个数超过108时会发生变异,则该种病毒细胞实验最
多进行的天数为
( )
(lg
2≈0.301
0)
A.25
B.26
C.27
D.28
C 令y=2t-1=108,故t-1=log2108=8log210,
即t=8log210+1=8
+1≈27.6,
故该种病毒细胞实验最多进行的天数为27.
4.(旅游纪念)甲乙丙丁四位同学一起到某地旅游,当地有A,B,C,D,E,F六种手工纪念品,他们打算每人买一种,甲说:只要不是A就行;乙说:C,D,E,F都行;丙说:我喜欢C,但是只要不是D就行;丁说:除了C,E之外,其他的都可以.据此判断,他们四人可以共同买的手工纪念品为________.?
【解析】甲可以选择的手工纪念品的集合为:{B,C,D,E,F},乙可以选择的手工纪念品的集合为{C,D,E,F},丙可以选择的手工纪念品的集合为{A,B,C,E,F},丁可以选择的手工纪念品的集合为{A,B,D,F},这四个集合的交集中只有元素F,故答案为F.
答案:F
【信息整理】
5.(信息安全)为了保证信息的安全传输,有一种为秘密密钥密码系统,其加密、解密原理为:发送方由明文到密文(加密),接收方由密文到明文(解密).现在加密密钥为y=xα(α为常数),如“4”通过加密后得到密文“2”.若接收方接到密文“3”,则解密后得到的明文
( )
A.4
B.6
C.8
D.9
D 由题目可知加密密钥y=xα(α是常数)是一个幂函数模型,所以要想求得解密
后得到的明文,就必须先求出α的值.由题意得2=4α,解得α=
,则y=
,由
=3,得x=9.
6.(瓷器)中国是世界上最古老的文明中心之一,中国古代对世界上最重要的贡献
之一就是发明了瓷器,中国陶瓷是世界上独一无二的.它的发展过程蕴藏着十分
丰富的科学和艺术,陶瓷形状各式各样,从不同角度诠释了数学中几何的形式之
美.现有一椭圆形明代瓷盘,经测量得到图中数据,则该椭圆瓷盘的焦距为
( )
A.8
cm
B.2
cm
C.4
cm
D.4
cm
C 根据椭圆的定义,得到:2a=8,解得a=4,2b=4,解得b=2,
所以c=
,所以焦距2c=4
(cm).
7.(粒子运动)如图,一个粒子从原点出发,在第一象限和两坐标轴
正半轴上运动,在第一秒时它从原点运动到点(0,1),接着它按图
所示在y轴、x轴的垂直方向上来回运动,且每秒移动一个单位长
度,那么,在2
018秒时,这个粒子所处的位置在点________.?
【解析】如图,设粒子运动到A1,A2,…,An时所用的时间分别为a1,a2,…,an,
则a1=2,a2=6,a3=12,a4=20,…,an-an-1=2n,
将a2-a1=2×2,a3-a2=2×3,a4-a3=2×4,…,an-an-1=2n相加得:
an-a1=2(2+3+4+…+n)=n2+n-2,则an=n(n+1),由44×45=1
980,故运动了1
980秒
时它到点A44(44,44),
又由运动规律知:A1,A2,…,An中,奇数点处向下运动,偶数点处向左运动,故粒子
到达A44(44,44)时向左运动38秒,即运动了2
018秒到达点(6,44),则所求点应为
(6,44).
答案:(6,44).
8.(学习强国)“学习强国”学习平台是由中宣部主管,以深入学习宣传习近平新
时代中国特色社会主义思想为主要内容,立足全体党员,面向全社会的优质平台,
现日益成为老百姓了解国家动态,紧跟时代脉博的热门APP,某市宣传部门为了解
全民利用“学习强国”了解国家动态的情况,从全市抽取2
000名人员进行调查,
统计他们每周利用“学习强国”的时长,如图是根据调查结果绘制的频率分布直
方图.
(1)根据频率分布直方图,求所有被抽查人员利用“学习强国”的平均时长和中
位数;
(2)宣传部为了了解大家利用“学习强国”的具体情况,准备采用分层抽样的方
法从[8,10)和[10,12)组中抽取50人了解情况,则两组各抽取多少人?再利用分层
抽样从抽取的50人中选5人参加一个座谈会.现从参加座谈会的5人中随机抽取两
人发言,求[10,12)组中至少有1人发言的概率.
【解析】(1)设被抽查人员利用“学习强国”的平均时长为
,中位数为y,
=0.05×1+0.1×3+0.25×5+0.3×7+0.15×9+0.1×11+0.05×13=6.8,0.05+
0.1+0.25+0.15×(y-6)=0.5,解得y=
,即被抽查人员利用“学习强国”的平均
时长为6.8,中位数为
.
(2)[8,10)组的人数为2
000×0.15=300,
设抽取的人数为a,[10,12)组的人数为2
000×0.1=200,设抽取的人数为b,
则
=
=
,解得a=30,b=20,
所以在[8,10)和[10,12)两组中分别抽取30人和20人,再抽取5人,两组分别抽取
3人和2人,将[8,10)组中被抽取的工作人员标记为A1,A2,A3,将[10,12)中的标记
为B1,B2.
设事件C表示从[10,12)组中至少抽取1人,
则抽取的情况如下:{A1,A2},{A1,A3},{A1,B1},{A1,B2},{A2,A3},{A2,B1},{A2,B2},{A3,B1},{A3,B2},
{B1,B2},共10种情况,
其中在[10,12)组中至少抽取1人的情况有7种,则
P(C)=
.
同课章节目录
