2021届高考数学二轮专题复习课件 探究新题型——“战疫”题(共28张PPT)
文档属性
| 名称 | 2021届高考数学二轮专题复习课件 探究新题型——“战疫”题(共28张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 989.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-19 22:18:47 | ||
图片预览



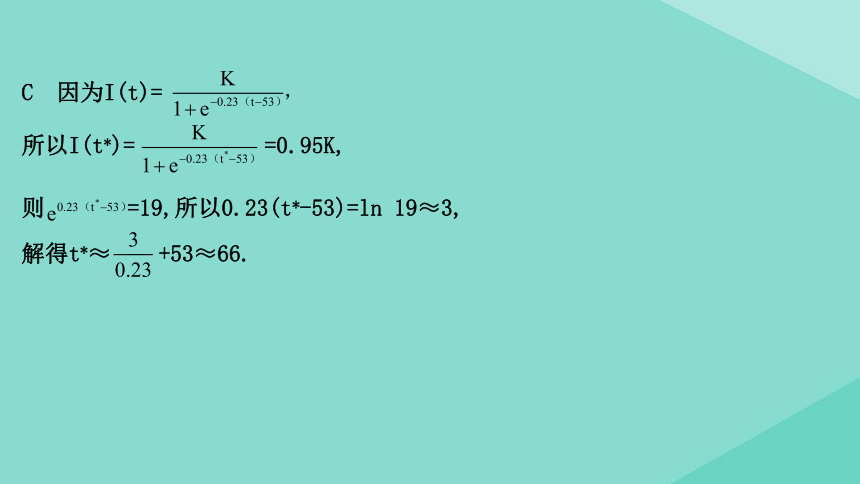




文档简介
探究新题型 “战疫”题
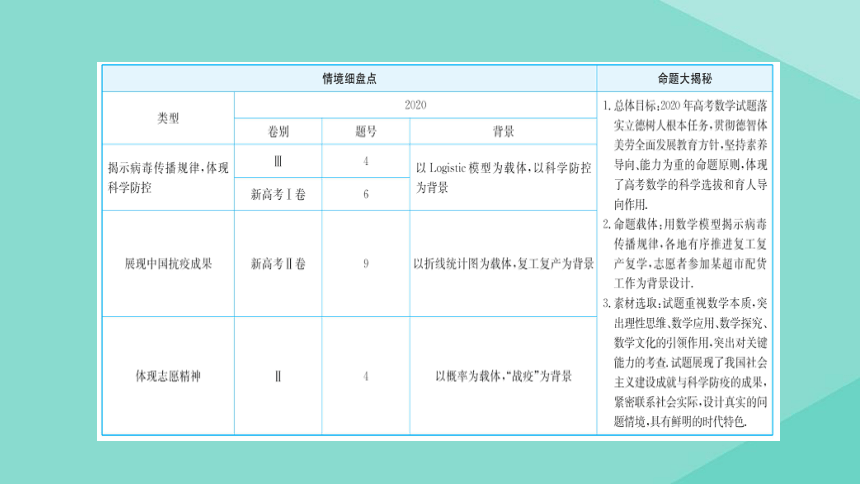
考向一 揭示病毒传播规律,体现科学防控
【典例1】(2020·全国Ⅲ卷)Logistic 模型是常用数学模型之
一,可应用于流行病学领域.有学者根据公布数据建立了某地区新冠肺炎累计确
诊病例数I(t)(t的单位:天)的Logistic模型:I(t)= ,其中K为最大确
诊病例数.当I(t*)=0.95K时,标志着已初步遏制疫情,则t*约为(ln 19≈3)
( )
A.60 B.63 C.66 D.69
真题再研析·提升审题力
试题
情境
以新冠肺炎疫情初始阶段累计确诊病例数的数学模型为背景,考查数学建模及指、对数运算.
学科
应用
在揭示病毒传播规律,体现科学防控中从数学的视角发现问题,提出问题,分析问题,建立模型,计算求解,从而解决问题.
关键
能力
逻辑思维能力:通过对模型的识别及数据收集、整理、分析,考查学生推理的能力.
运算求解能力:通过指、对数的运算,方程的求解,考查数学运算的能力.
C 因为I(t)=
所以I(t*)= =0.95K,
则 =19,所以0.23(t*-53)=ln 19≈3,
解得t*≈ +53≈66.
考向二 体现志愿精神
【典例2】(2020·全国Ⅱ卷) 在新冠肺炎疫情防控期间,某超市开通网上销售业
务,每天能完成1 200份订单的配货,由于订单量大幅增加,导致订单积压.为解决
困难,许多志愿者踊跃报名参加配货工作.已知该超市某日积压500份订单未配货,
预计第二天的新订单超过1 600份的概率为0.05.志愿者每人每天能完成50份订
单的配货,为使第二天完成积压订单及当日订单的配货的概率不小于0.95,则至
少需要志愿者 ( )
A.10名 B.18名 C.24名 D.32名
试题
情境
以志愿者参加某超市配货工作为背景设计的数学问题,考查概率的运用.
学科
应用
本题从数学角度对志愿者在超市配货工作中的问题进行解读,体现了数学在实际生活中的应用.
关键
能力
逻辑思维能力:本题涉及至少需要志愿者的数量,要将订单数和志愿服务的人数联想、推理,要求学生运用所学知识解决实践中遇到的问题.
数学建模能力:运用题干提供的数据建立模型进行计算求解.
B (1 600+500-1 200)÷50=18(名).
1.(“战疫”与排列组合)2020年春节永生难忘,突如其来的疫情,
让湖北省武汉市陷入风波巨浪的中心.一方有难、八方支援,
中国人民万众一心,众志成城,一定能够打赢这场没有硝烟的保卫生命健康之战.
某医疗机构医务特勤班有4名医务人员报名参加甲、乙、丙三所医院的应急应聘
考试,每人限报一所医院,若这三所医院中每所医院都至少有1名医务人员报考,
则这4名医务人员不同的报考方法共有 ( )
A.18种 B.81种 C.36种 D.64种
高考演兵场·检验考试力
C 据题意知,所求不同的报考方法数m= (种).
2.(“战疫”与随机抽样)2020年初,我国突发新冠肺炎疫情,疫情期间中小学生
“停课不停学”.已知某地区中小学生人数情况如甲图所示,各学段学生在疫情
期间“家务劳动”的参与率如乙图所示.为了进一步了解该地区中小学生参与
“家务劳动”的情况,现用分层抽样的方法抽取4%小学、初中、高中学段的学生
进行调查,则抽取的样本容量、抽取的高中生中参与“家务劳动”的人数分别为
( )
A.2 750,200 B.2 750,110 C.1 120,110 D.1 120,200
C 由题意得,抽取的样本容量为(15 500+7 500+5 000)×4%=1 120,抽取的高中生中参与“家务劳动”的人数为5 000×4%×0.55=110.
3.(“战疫”与回归分析)2020年初,新型冠状病毒引起的肺炎疫情暴发以来,各
地医疗机构采取了各种针对性的治疗方法,取得了不错的成效,某地开始使用中
西医结合的方法后,每周治愈的患者人数如表所示:
由表格可得y关于x的回归方程为 ,则此回归模型第4周的残差(实际值
与预报值之差)为 ( )
A.5 B.-13 C.13 D.0
周数(x)
1
2
3
4
5
治愈人数(y)
2
17
36
103
142
C 设t=x2,则 =11,
=60,
a=60-6×11=-6,所以 =6x2-6.
令x=4,得e4=y4- 4=103-6×42+6=13.
4.(“战疫”与数列)有关部门往往会采用一个系数K来评估一次疫情蔓延的程度,就是指在无任何干预下,平均一个感染者每天能传播K个人,若K=3,则一个感染者传播3亿人至少需要经过(lg3≈0.477,lg2≈0.301) ( )
A.8天 B.12天
C.15天 D.18天
C 设第一天感染人数为a1=4,第n天感染的人数为an,
则an=an-1+an-1×3? =4(n≥2),
所以an=4×4n-1>3×108,
两边取对数得:nlg 4>lg 3+8,解得:n>14.08,
所以一个感染者传播3亿人至少需要经过15天.
5.(“战疫”与解三角形)2020年新型冠状病毒肺炎蔓延全国,作为主要战场的武
汉,仅用了十余天就建成了“小汤山”模式的火神山医院和雷神山医院,再次体
现了中国速度.随着疫情发展,某地也需要参照“小汤山”模式建设临时医院,其
占地是一个正方形和四个以正方形的边为底边、腰长为400 m的等腰三角形组成
的图形(如图所示),为使占地面积最大,则等腰三角形的底角为 ( )
A. B.
C. D.
D 设顶角为α,由三角形的面积公式可得4个等腰三角形的面积和为4×
×400×400sin α,由余弦定理可得正方形边长为
=400
故正方形面积为160 000(2-2cos α)=320 000(1-cos α),
所以所求占地面积为320 000(1-cos α+sin α)
=320 000
所以当α- 即α= 时,占地面积最大,此时底角为
6.(“战疫”与概率)现有三张识字卡片,分别写有“抗”“疫”“情”这三个字.将这三张卡片随机排序,则能组成“抗疫情”的概率是________.?
【解析】由题得“抗”“疫”“情”这三个字的排列有:抗疫情,抗情疫,疫抗情,
疫情抗,情抗疫,情疫抗,共有6种,其中,组成“抗疫情”的只有1种.故能组成
“抗疫情”的概率是P= .
答案:
7.(“战疫”与线性规划)2020年春节期间,因新冠肺炎疫情防控工作需要,某中
学需要安排男教师x名,女教师y名做义工,x和y需满足条件
则该校最多安排教师______人.?
【解析】由于x和y需满足约束条件 画出可行域为:
对于需要求该校安排的教师人数最多,目标函数为z=x+y,
得y=-x+z,
则题意转化为:在可行域内任意取x,y且为整数,
使得目标函数的斜率为定值-1,截距最大时的直线为过
的交点(6,7),
因为x<6,所以当直线z=x+y经过点A(5,5)时,z取最大值,即zmax=5+5=10.
答案:10
8.(“战疫”与统计案例)疫情无情人有情,为了响应国家“不出门,不串门,不聚
餐”的号召,自疫情发生以来,学生主要在家学习,此时学习积极性显得至关重要,
为了了解学生的学习积极性和观看电视节目的相关性,对某班50名学生的学习积
极性和观看电视节目情况进行了调查,得到的统计数据如表所示.
学习积极性高
学习积极性一般
总计
不观看电视节目
28
观看电视节目
17
总计
25
50
(1)请把表格数据补充完整,并运用独立性检验的思想方法,判断能否在犯错误的概率不超过0.001的前提下认为学生的学习积极性与是否观看电视节目有关系?
(2)若从不观看电视节目的28人中按照学习积极性进行分层抽样,抽取7人,再从这7人中随机选取2人作为代表发言,求恰有1人学习积极性高的概率.
【解析】(1)根据题意,补充列联表如下;
学习积极性高
学习积极性一般
总计
不观看电视节目
20
8
28
观看电视节目
5
17
22
总计
25
25
50
根据表中数据,计算K2的观测值k=
≈11.688>10.828,
所以能在犯错误的概率不超过0.001的前提下认为学生的学习积极性与是否观看
电视节目有关系;
(2)由题意知抽样比例为
所以抽取的7人中,学习积极性高的有 =5人,记为a、b、c、d、e,
学习积极性一般的有7-5=2人,记为F、G,
从这7人中随机选取2人,基本事件为:
ab、ac、ad、ae、aF、aG、bc、bd、be、bF、bG、cd、ce、cF、cG、de、dF、
dG、eF、eG、FG共21种,其中恰有1人学习积极性高的基本事件为:aF、aG、bF、
bG、cF、cG、dF、dG、eF、eG共10种,故所求的概率值为P= .
考向一 揭示病毒传播规律,体现科学防控
【典例1】(2020·全国Ⅲ卷)Logistic 模型是常用数学模型之
一,可应用于流行病学领域.有学者根据公布数据建立了某地区新冠肺炎累计确
诊病例数I(t)(t的单位:天)的Logistic模型:I(t)= ,其中K为最大确
诊病例数.当I(t*)=0.95K时,标志着已初步遏制疫情,则t*约为(ln 19≈3)
( )
A.60 B.63 C.66 D.69
真题再研析·提升审题力
试题
情境
以新冠肺炎疫情初始阶段累计确诊病例数的数学模型为背景,考查数学建模及指、对数运算.
学科
应用
在揭示病毒传播规律,体现科学防控中从数学的视角发现问题,提出问题,分析问题,建立模型,计算求解,从而解决问题.
关键
能力
逻辑思维能力:通过对模型的识别及数据收集、整理、分析,考查学生推理的能力.
运算求解能力:通过指、对数的运算,方程的求解,考查数学运算的能力.
C 因为I(t)=
所以I(t*)= =0.95K,
则 =19,所以0.23(t*-53)=ln 19≈3,
解得t*≈ +53≈66.
考向二 体现志愿精神
【典例2】(2020·全国Ⅱ卷) 在新冠肺炎疫情防控期间,某超市开通网上销售业
务,每天能完成1 200份订单的配货,由于订单量大幅增加,导致订单积压.为解决
困难,许多志愿者踊跃报名参加配货工作.已知该超市某日积压500份订单未配货,
预计第二天的新订单超过1 600份的概率为0.05.志愿者每人每天能完成50份订
单的配货,为使第二天完成积压订单及当日订单的配货的概率不小于0.95,则至
少需要志愿者 ( )
A.10名 B.18名 C.24名 D.32名
试题
情境
以志愿者参加某超市配货工作为背景设计的数学问题,考查概率的运用.
学科
应用
本题从数学角度对志愿者在超市配货工作中的问题进行解读,体现了数学在实际生活中的应用.
关键
能力
逻辑思维能力:本题涉及至少需要志愿者的数量,要将订单数和志愿服务的人数联想、推理,要求学生运用所学知识解决实践中遇到的问题.
数学建模能力:运用题干提供的数据建立模型进行计算求解.
B (1 600+500-1 200)÷50=18(名).
1.(“战疫”与排列组合)2020年春节永生难忘,突如其来的疫情,
让湖北省武汉市陷入风波巨浪的中心.一方有难、八方支援,
中国人民万众一心,众志成城,一定能够打赢这场没有硝烟的保卫生命健康之战.
某医疗机构医务特勤班有4名医务人员报名参加甲、乙、丙三所医院的应急应聘
考试,每人限报一所医院,若这三所医院中每所医院都至少有1名医务人员报考,
则这4名医务人员不同的报考方法共有 ( )
A.18种 B.81种 C.36种 D.64种
高考演兵场·检验考试力
C 据题意知,所求不同的报考方法数m= (种).
2.(“战疫”与随机抽样)2020年初,我国突发新冠肺炎疫情,疫情期间中小学生
“停课不停学”.已知某地区中小学生人数情况如甲图所示,各学段学生在疫情
期间“家务劳动”的参与率如乙图所示.为了进一步了解该地区中小学生参与
“家务劳动”的情况,现用分层抽样的方法抽取4%小学、初中、高中学段的学生
进行调查,则抽取的样本容量、抽取的高中生中参与“家务劳动”的人数分别为
( )
A.2 750,200 B.2 750,110 C.1 120,110 D.1 120,200
C 由题意得,抽取的样本容量为(15 500+7 500+5 000)×4%=1 120,抽取的高中生中参与“家务劳动”的人数为5 000×4%×0.55=110.
3.(“战疫”与回归分析)2020年初,新型冠状病毒引起的肺炎疫情暴发以来,各
地医疗机构采取了各种针对性的治疗方法,取得了不错的成效,某地开始使用中
西医结合的方法后,每周治愈的患者人数如表所示:
由表格可得y关于x的回归方程为 ,则此回归模型第4周的残差(实际值
与预报值之差)为 ( )
A.5 B.-13 C.13 D.0
周数(x)
1
2
3
4
5
治愈人数(y)
2
17
36
103
142
C 设t=x2,则 =11,
=60,
a=60-6×11=-6,所以 =6x2-6.
令x=4,得e4=y4- 4=103-6×42+6=13.
4.(“战疫”与数列)有关部门往往会采用一个系数K来评估一次疫情蔓延的程度,就是指在无任何干预下,平均一个感染者每天能传播K个人,若K=3,则一个感染者传播3亿人至少需要经过(lg3≈0.477,lg2≈0.301) ( )
A.8天 B.12天
C.15天 D.18天
C 设第一天感染人数为a1=4,第n天感染的人数为an,
则an=an-1+an-1×3? =4(n≥2),
所以an=4×4n-1>3×108,
两边取对数得:nlg 4>lg 3+8,解得:n>14.08,
所以一个感染者传播3亿人至少需要经过15天.
5.(“战疫”与解三角形)2020年新型冠状病毒肺炎蔓延全国,作为主要战场的武
汉,仅用了十余天就建成了“小汤山”模式的火神山医院和雷神山医院,再次体
现了中国速度.随着疫情发展,某地也需要参照“小汤山”模式建设临时医院,其
占地是一个正方形和四个以正方形的边为底边、腰长为400 m的等腰三角形组成
的图形(如图所示),为使占地面积最大,则等腰三角形的底角为 ( )
A. B.
C. D.
D 设顶角为α,由三角形的面积公式可得4个等腰三角形的面积和为4×
×400×400sin α,由余弦定理可得正方形边长为
=400
故正方形面积为160 000(2-2cos α)=320 000(1-cos α),
所以所求占地面积为320 000(1-cos α+sin α)
=320 000
所以当α- 即α= 时,占地面积最大,此时底角为
6.(“战疫”与概率)现有三张识字卡片,分别写有“抗”“疫”“情”这三个字.将这三张卡片随机排序,则能组成“抗疫情”的概率是________.?
【解析】由题得“抗”“疫”“情”这三个字的排列有:抗疫情,抗情疫,疫抗情,
疫情抗,情抗疫,情疫抗,共有6种,其中,组成“抗疫情”的只有1种.故能组成
“抗疫情”的概率是P= .
答案:
7.(“战疫”与线性规划)2020年春节期间,因新冠肺炎疫情防控工作需要,某中
学需要安排男教师x名,女教师y名做义工,x和y需满足条件
则该校最多安排教师______人.?
【解析】由于x和y需满足约束条件 画出可行域为:
对于需要求该校安排的教师人数最多,目标函数为z=x+y,
得y=-x+z,
则题意转化为:在可行域内任意取x,y且为整数,
使得目标函数的斜率为定值-1,截距最大时的直线为过
的交点(6,7),
因为x<6,所以当直线z=x+y经过点A(5,5)时,z取最大值,即zmax=5+5=10.
答案:10
8.(“战疫”与统计案例)疫情无情人有情,为了响应国家“不出门,不串门,不聚
餐”的号召,自疫情发生以来,学生主要在家学习,此时学习积极性显得至关重要,
为了了解学生的学习积极性和观看电视节目的相关性,对某班50名学生的学习积
极性和观看电视节目情况进行了调查,得到的统计数据如表所示.
学习积极性高
学习积极性一般
总计
不观看电视节目
28
观看电视节目
17
总计
25
50
(1)请把表格数据补充完整,并运用独立性检验的思想方法,判断能否在犯错误的概率不超过0.001的前提下认为学生的学习积极性与是否观看电视节目有关系?
(2)若从不观看电视节目的28人中按照学习积极性进行分层抽样,抽取7人,再从这7人中随机选取2人作为代表发言,求恰有1人学习积极性高的概率.
【解析】(1)根据题意,补充列联表如下;
学习积极性高
学习积极性一般
总计
不观看电视节目
20
8
28
观看电视节目
5
17
22
总计
25
25
50
根据表中数据,计算K2的观测值k=
≈11.688>10.828,
所以能在犯错误的概率不超过0.001的前提下认为学生的学习积极性与是否观看
电视节目有关系;
(2)由题意知抽样比例为
所以抽取的7人中,学习积极性高的有 =5人,记为a、b、c、d、e,
学习积极性一般的有7-5=2人,记为F、G,
从这7人中随机选取2人,基本事件为:
ab、ac、ad、ae、aF、aG、bc、bd、be、bF、bG、cd、ce、cF、cG、de、dF、
dG、eF、eG、FG共21种,其中恰有1人学习积极性高的基本事件为:aF、aG、bF、
bG、cF、cG、dF、dG、eF、eG共10种,故所求的概率值为P= .
同课章节目录
