专题六 第3讲 母题突破2 定点问题(共34张PPT)2021届高考数学二轮复习 课件
文档属性
| 名称 | 专题六 第3讲 母题突破2 定点问题(共34张PPT)2021届高考数学二轮复习 课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-19 22:17:51 | ||
图片预览






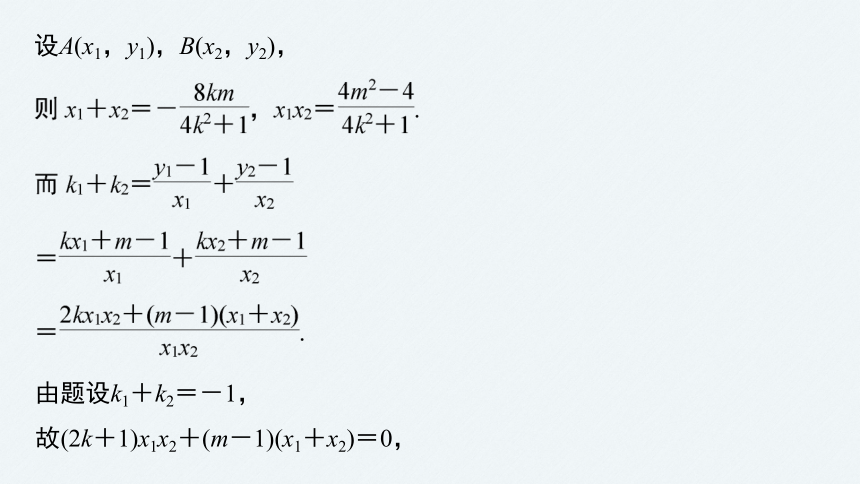
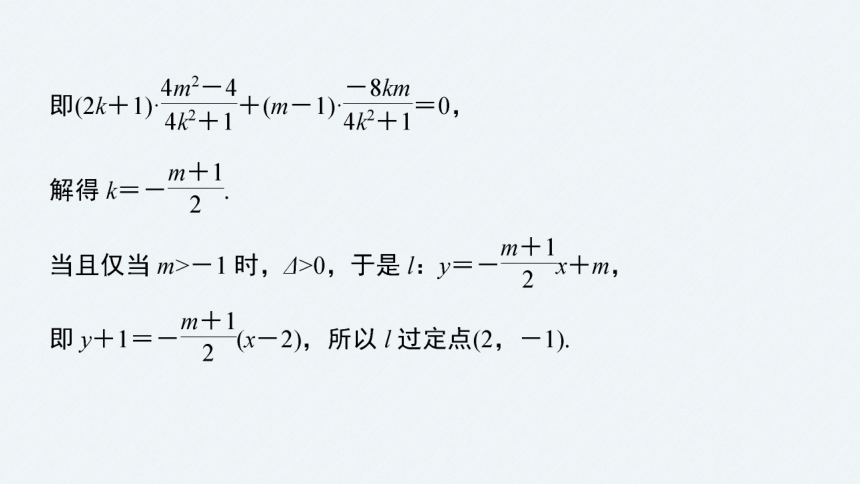




文档简介
专题六 第3讲 圆锥曲线的综合问题
母题突破2 定点问题
内
容
索
引
母题突破2
专题强化练
1
母题突破2 定点问题
PART ONE
母题 已知椭圆C: +y2=1,点P(0,1),设直线l不经过P点且与C
相交于A,B两点,若直线PA与直线PB的斜率的和为-1,求证:l过定点.
思路分析
?l斜率k存在时写出l的方程
↓
?联立l,C的方程,设而不求
↓
?计算kPA,kPB并代入kPA+kPB=-1
↓
?分析直线方程,找出定点
证明 设直线PA与直线PB的斜率分别为k1,k2.
如果l与x轴垂直,设l:x=t,由题设知t≠0,且|t|<2,
从而可设l:y=kx+m(m≠1).
由题设可知Δ=16(4k2-m2+1)>0.
设A(x1,y1),B(x2,y2),
由题设k1+k2=-1,
故(2k+1)x1x2+(m-1)(x1+x2)=0,
子题1 已知抛物线C:y2=4x的焦点为F,直线l与抛物线C交于A,B两点,O是坐标原点.若点E(-2,0),直线l不与坐标轴垂直,且∠AEO=∠BEO,求证:直线l过定点.
证明 设A(x1,y1),B(x2,y2),由题意可设直线l的方程为x=ny+b(n≠0),
则y1+y2=4n,y1y2=-4b.
由∠AEO=∠BEO,得kEA=-kEB,
整理得y1x2+2y1+x1y2+2y2=0,
即y1(ny2+b)+2y1+(ny1+b)y2+2y2=0,
整理得2ny1y2+(b+2)(y1+y2)=0,
即-8bn+4(b+2)n=0,得b=2,
故直线l的方程为x=ny+2(n≠0),
所以直线l过定点(2,0).
证明 由题意可知,直线l的斜率不为0,设其方程为x=my+2(m∈R),
将x=my+2代入y2=4x,消去x可得y2-4my-8=0,
显然Δ=16m2+32>0,设M(x1,y1),N(x2,y2),
则y1+y2=4m,y1y2=-8,
所以P(2m2+2,2m),
又PQ⊥y轴,垂足为Q,所以Q(0,2m),
设以PQ为直径的圆经过点A(x0,y0),
所以当x0=2,y0=0时,对任意的m∈R,①式恒成立,
所以以PQ为直径的圆过定点,该定点的坐标为(2,0).
规律方法
动线过定点问题的两大类型及解法
(1)动直线l过定点问题,解法:设动直线方程(斜率存在)为y=kx+t,由题设条件将t用k表示为t=mk,得y=k(x+m),故动直线过定点(-m,0).
(2)动曲线C过定点问题,解法:引入参变量建立曲线C的方程,再根据其对参变量恒成立,令其系数等于零,得出定点.
跟踪演练
1.(2020·北京东城区模拟)已知椭圆C: =1的右焦点为F,直线l:
y=kx+m(k≠0)过点F,且与椭圆C交于P,Q两点,如果点P关于x轴的对称点为P′,求证:直线P′Q过x轴上的定点.
直线l:y=kx+m(k≠0)过点F,
∴m=-2k,∴l:y=k(x-2).
设P(x1,y1),Q(x2,y2),
∵点P关于x轴的对称点为P′,则P′(x1,-y1).
∴直线P′Q过x轴上的定点(3,0).
(1)求椭圆的方程;
(2)过点P的两条直线l1,l2分别与C相交于不同于点P的A,B两点,若l1与l2的斜率之和为-4,则直线AB是否经过定点?若是,求出定点坐标;若不过定点,请说明理由.
解 当直线AB的斜率存在时,
设直线AB的方程为y=kx+t(t≠2),A(x1,y1),B(x2,y2),
可得(3k2+2)x2+6ktx+3t2-12=0,
∴Δ=36(kt)2-4×(3k2+2)(3t2-12)>0,
即24(6k2-t2+4)>0,
由l1与l2的斜率之和为-4,
又y1=kx1+t,y2=kx2+t,
∵t≠2,化简可得t=-k-2,
∴y=kx-k-2=k(x-1)-2,
∴直线AB经过定点(1,-2).
当直线AB的斜率不存在时,
设直线AB的方程为x=m,A(m,y1),B(m,y2),
又点A,B均在椭圆上,
∴A,B关于x轴对称,∴y1+y2=0,∴m=1,
故直线AB的方程为x=1,也过点(1,-2),
综上直线AB经过定点,定点为(1,-2).
2
专题强化练
PART TWO
1
2
证明 ①当直线l的斜率不存在时,设l:x=m,A(m,yA),B(m,-yA),
②当直线l的斜率存在时,设l:y=kx+b(b≠-1),
A(x1,y1),B(x2,y2),
1
2
依题意得,Δ>0,
1
2
1
2
所以直线l恒过定点(0,-2).
1
2.已知点H为抛物线C:x2=4y的准线上任一点,过H作抛物线C的两条切线HA,HB,切点为A,B,证明直线AB过定点,并求△HAB面积的最小值.
2
解 设点A(x1,y1),B(x2,y2),H(t,-1),
1
2
即直线AB恒过抛物线的焦点F(0,1),
当t=0时,此时H(0,-1),可知HF⊥AB,
1
2
1
2
|AB|=y1+y2+2=t2+4,
综上所述,当t=0时,S△HAB最小,且最小值为4.
本课结束
母题突破2 定点问题
内
容
索
引
母题突破2
专题强化练
1
母题突破2 定点问题
PART ONE
母题 已知椭圆C: +y2=1,点P(0,1),设直线l不经过P点且与C
相交于A,B两点,若直线PA与直线PB的斜率的和为-1,求证:l过定点.
思路分析
?l斜率k存在时写出l的方程
↓
?联立l,C的方程,设而不求
↓
?计算kPA,kPB并代入kPA+kPB=-1
↓
?分析直线方程,找出定点
证明 设直线PA与直线PB的斜率分别为k1,k2.
如果l与x轴垂直,设l:x=t,由题设知t≠0,且|t|<2,
从而可设l:y=kx+m(m≠1).
由题设可知Δ=16(4k2-m2+1)>0.
设A(x1,y1),B(x2,y2),
由题设k1+k2=-1,
故(2k+1)x1x2+(m-1)(x1+x2)=0,
子题1 已知抛物线C:y2=4x的焦点为F,直线l与抛物线C交于A,B两点,O是坐标原点.若点E(-2,0),直线l不与坐标轴垂直,且∠AEO=∠BEO,求证:直线l过定点.
证明 设A(x1,y1),B(x2,y2),由题意可设直线l的方程为x=ny+b(n≠0),
则y1+y2=4n,y1y2=-4b.
由∠AEO=∠BEO,得kEA=-kEB,
整理得y1x2+2y1+x1y2+2y2=0,
即y1(ny2+b)+2y1+(ny1+b)y2+2y2=0,
整理得2ny1y2+(b+2)(y1+y2)=0,
即-8bn+4(b+2)n=0,得b=2,
故直线l的方程为x=ny+2(n≠0),
所以直线l过定点(2,0).
证明 由题意可知,直线l的斜率不为0,设其方程为x=my+2(m∈R),
将x=my+2代入y2=4x,消去x可得y2-4my-8=0,
显然Δ=16m2+32>0,设M(x1,y1),N(x2,y2),
则y1+y2=4m,y1y2=-8,
所以P(2m2+2,2m),
又PQ⊥y轴,垂足为Q,所以Q(0,2m),
设以PQ为直径的圆经过点A(x0,y0),
所以当x0=2,y0=0时,对任意的m∈R,①式恒成立,
所以以PQ为直径的圆过定点,该定点的坐标为(2,0).
规律方法
动线过定点问题的两大类型及解法
(1)动直线l过定点问题,解法:设动直线方程(斜率存在)为y=kx+t,由题设条件将t用k表示为t=mk,得y=k(x+m),故动直线过定点(-m,0).
(2)动曲线C过定点问题,解法:引入参变量建立曲线C的方程,再根据其对参变量恒成立,令其系数等于零,得出定点.
跟踪演练
1.(2020·北京东城区模拟)已知椭圆C: =1的右焦点为F,直线l:
y=kx+m(k≠0)过点F,且与椭圆C交于P,Q两点,如果点P关于x轴的对称点为P′,求证:直线P′Q过x轴上的定点.
直线l:y=kx+m(k≠0)过点F,
∴m=-2k,∴l:y=k(x-2).
设P(x1,y1),Q(x2,y2),
∵点P关于x轴的对称点为P′,则P′(x1,-y1).
∴直线P′Q过x轴上的定点(3,0).
(1)求椭圆的方程;
(2)过点P的两条直线l1,l2分别与C相交于不同于点P的A,B两点,若l1与l2的斜率之和为-4,则直线AB是否经过定点?若是,求出定点坐标;若不过定点,请说明理由.
解 当直线AB的斜率存在时,
设直线AB的方程为y=kx+t(t≠2),A(x1,y1),B(x2,y2),
可得(3k2+2)x2+6ktx+3t2-12=0,
∴Δ=36(kt)2-4×(3k2+2)(3t2-12)>0,
即24(6k2-t2+4)>0,
由l1与l2的斜率之和为-4,
又y1=kx1+t,y2=kx2+t,
∵t≠2,化简可得t=-k-2,
∴y=kx-k-2=k(x-1)-2,
∴直线AB经过定点(1,-2).
当直线AB的斜率不存在时,
设直线AB的方程为x=m,A(m,y1),B(m,y2),
又点A,B均在椭圆上,
∴A,B关于x轴对称,∴y1+y2=0,∴m=1,
故直线AB的方程为x=1,也过点(1,-2),
综上直线AB经过定点,定点为(1,-2).
2
专题强化练
PART TWO
1
2
证明 ①当直线l的斜率不存在时,设l:x=m,A(m,yA),B(m,-yA),
②当直线l的斜率存在时,设l:y=kx+b(b≠-1),
A(x1,y1),B(x2,y2),
1
2
依题意得,Δ>0,
1
2
1
2
所以直线l恒过定点(0,-2).
1
2.已知点H为抛物线C:x2=4y的准线上任一点,过H作抛物线C的两条切线HA,HB,切点为A,B,证明直线AB过定点,并求△HAB面积的最小值.
2
解 设点A(x1,y1),B(x2,y2),H(t,-1),
1
2
即直线AB恒过抛物线的焦点F(0,1),
当t=0时,此时H(0,-1),可知HF⊥AB,
1
2
1
2
|AB|=y1+y2+2=t2+4,
综上所述,当t=0时,S△HAB最小,且最小值为4.
本课结束
同课章节目录
