(导学教程)2012届高三数学(理)二轮复习试题:专题七第一讲综合验收评估(北师大版)
文档属性
| 名称 | (导学教程)2012届高三数学(理)二轮复习试题:专题七第一讲综合验收评估(北师大版) |  | |
| 格式 | zip | ||
| 文件大小 | 400.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-01 23:11:47 | ||
图片预览

文档简介
一、选择题
1.(2011·汕头模拟)从球外一点引球的切线,则
A.可以引无数条切线,所有切点组成球的一个大圆
B.可以引无数条切线,所有切点组成球的一个小圆
C.只可以引两条切线,两切点的连线过球心
D.只可以引两条切线,两切点的连线不过球心
解析 从球外一点可以引球的无数条切线,所有切点组成球的一个小圆.
答案 B
2.从不在⊙O上的一点A作直线交⊙O于B、C,且AB·AC=64,OA=10,则⊙O的半径等于
A.2 B.6
C.2或6 D.8或
解析 设圆O的半径为r,当点在圆外时,由切割线定理得AB·AC=64=(10+r)(10-r),解得r=6,当点在圆内时,由相交弦定理得AB·AC=64=(r+10)(r-10),解得r=2.
答案 C
3.如图所示,⊙O的割线PAB交⊙O于A,B两点,割线PCD经过圆心,已知PA=6,AB=7,PO=12,则⊙O的半径为
A.8 B.2
C.6 D.
解析 设圆的半径为r,根据割线定理,
得PA·PB=PC·PD,
即6×=(12-r)(12+r),解得r=8.
答案 A
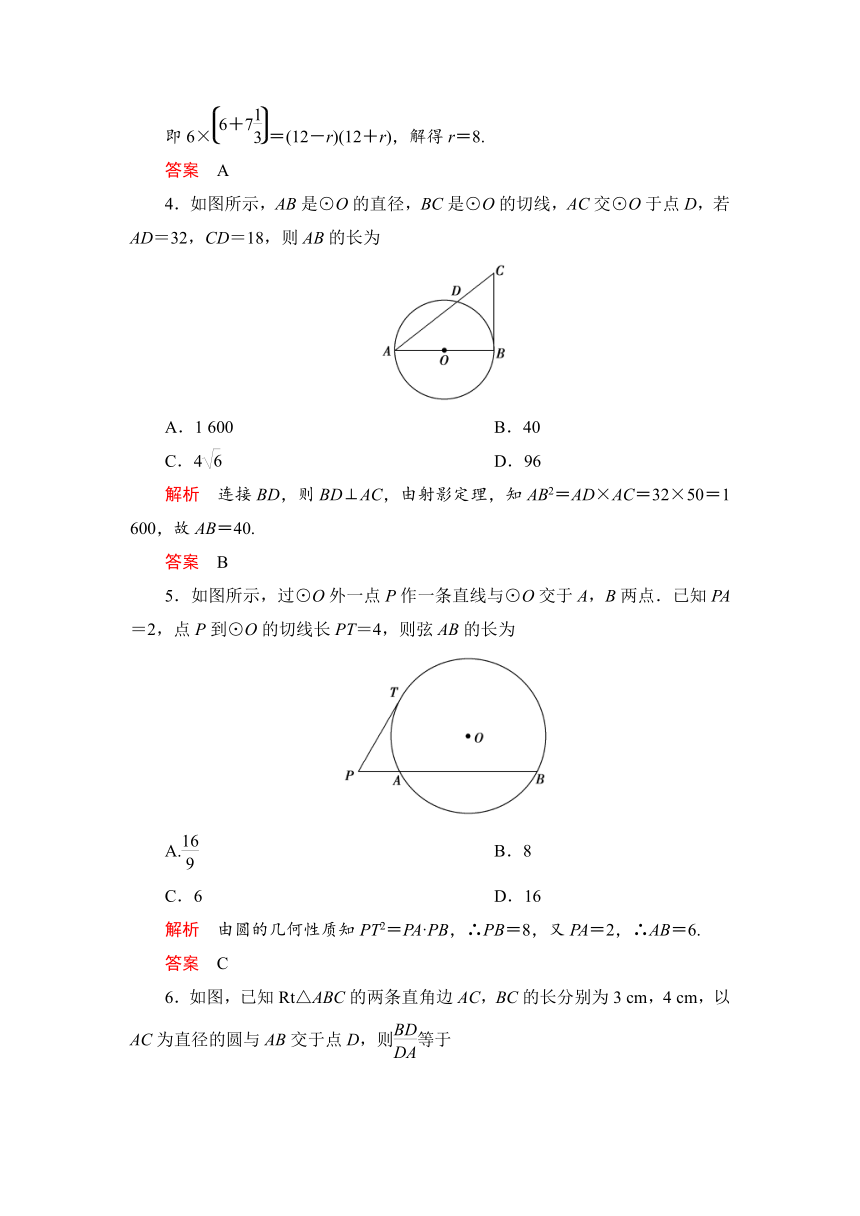
4.如图所示,AB是⊙O的直径,BC是⊙O的切线,AC交⊙O于点D,若AD=32,CD=18,则AB的长为
A.1 600 B.40
C.4 D.96
解析 连接BD,则BD⊥AC,由射影定理,知AB2=AD×AC=32×50=1 600,故AB=40.
答案 B
5.如图所示,过⊙O外一点P作一条直线与⊙O交于A,B两点.已知PA=2,点P到⊙O的切线长PT=4,则弦AB的长为
A. B.8
C.6 D.16
解析 由圆的几何性质知PT2=PA·PB,∴PB=8,又PA=2,∴AB=6.
答案 C
6.如图,已知Rt△ABC的两条直角边AC,BC的长分别为3 cm,4 cm,以AC为直径的圆与AB交于点D,则等于
A.4 B.6
C.9 D.
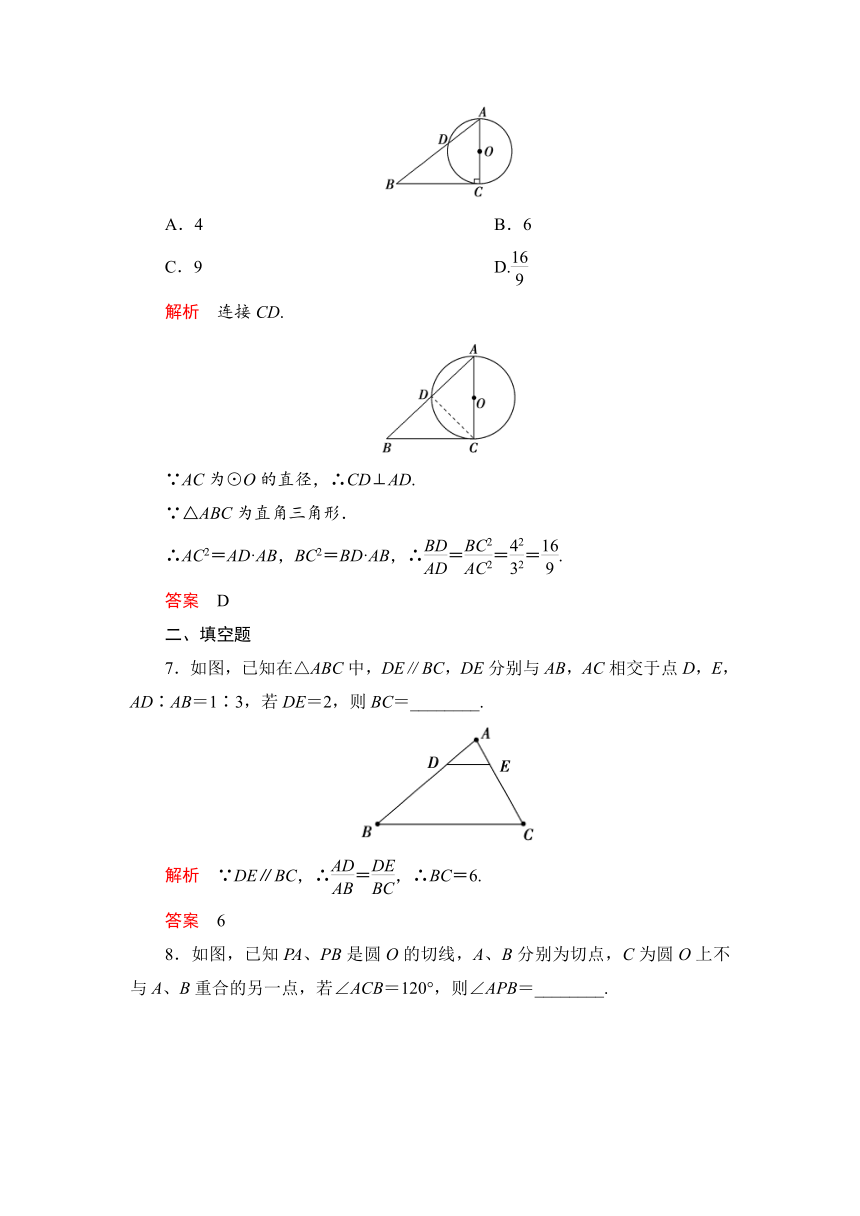
解析 连接CD.
∵AC为⊙O的直径,∴CD⊥AD.
∵△ABC为直角三角形.
∴AC2=AD·AB,BC2=BD·AB,∴===.
答案 D
二、填空题
7.如图,已知在△ABC中,DE∥BC,DE分别与AB,AC相交于点D,E,AD∶AB=1∶3,若DE=2,则BC=________.
解析 ∵DE∥BC,∴=,∴BC=6.
答案 6
8.如图,已知PA、PB是圆O的切线,A、B分别为切点,C为圆O上不与A、B重合的另一点,若∠ACB=120°,则∠APB=________.
解析 连接OA、OB,∠PAO=∠PBO=90°,
∵∠ACB=120°,∴∠AOB=120°.
又P、A、O、B四点共圆,故∠APB=60°.
答案 60°
9.如图,点P在圆O直径AB的延长线上,且PB=OB=2,PC切圆O于C点,CD⊥AB于D点,则CD=________.
解析 由切割线定理知,
PC2=PA·PB,解得PC=2.
又OC⊥PC,故CD===.
答案
三、解答题
10.(2011·大连重点中学第二次联考)如图所示,AB是⊙O的直径,弦BD、CA的延长线相交于点E,EF垂直BA的延长线于点F.
求证:(1)∠DEA=∠DFA;
(2)AB2=BE·BD-AE·AC.
证明 (1)连接AD.
∵AB为⊙O的直径,
∴∠ADB=90°,即∠EDA=90°.
又EF⊥AB,∠EFA=90°,
则A、D、E、F四点共圆,∴∠DEA=∠DFA.
(2)由(1),知BD·BE=BA·BF,
又△ABC∽△AEF,∴=,
即AB·AF=AE·AC.
∴BE·BD-AE·AC=BA·BF-AB·AF=AB(BF-AF)=AB2.
11.如图,BD、CE是△ABC的高.求证:ADE∽△ABC.
证明 ∵BD、CE是△ABC的高,∴∠AEC=∠ADB=90°.
又∵∠A=∠A,∴△AEC∽△ADB,∴=.
又∵∠A=∠A,∴△ADE∽△ABC.
12.(2011·课标全国卷)如图,D,E分别为△ABC的边AB,AC上的点,且不与△ABC的顶点重合.已知AE的长为m,AC的长为n,AD,AB的长是关于x的方程x2-14x+mn=0的两个根.
(1)证明:C,B,D,E四点共圆;
(2)若∠A=90°,且m=4,n=6,求C,B,D,E所在圆的半径.
解析 (1)证明 如图,连接DE,在△ADE和△ACB中,AD·AB=mn=AE·AC,即=.又∠DAE=∠CAB,从而△ADE∽△ACB.
因此∠ADE=∠ACB.所以C,B,D,E四点共圆.
(2)m=4,n=6时,方程x2-14x+mn=0的两根为x1=2,x2=12.故AD=2,AB=12.
如图,取CE的中点G,DB的中点F,分别过G,F作AC,AB的垂线,两垂线相交于H点,连接DH.因为C,B,D,E四点共圆,所以C,B,D,E四点所在圆的圆心为H,半径为DH.
由于∠A=90°,故GH∥AB,HF∥AC.
从而HF=AG=5,DF=(12-2)=5.
故C,B,D,E四点所在圆的半径为5.
.精品资料。欢迎使用。 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
1.(2011·汕头模拟)从球外一点引球的切线,则
A.可以引无数条切线,所有切点组成球的一个大圆
B.可以引无数条切线,所有切点组成球的一个小圆
C.只可以引两条切线,两切点的连线过球心
D.只可以引两条切线,两切点的连线不过球心
解析 从球外一点可以引球的无数条切线,所有切点组成球的一个小圆.
答案 B
2.从不在⊙O上的一点A作直线交⊙O于B、C,且AB·AC=64,OA=10,则⊙O的半径等于
A.2 B.6
C.2或6 D.8或
解析 设圆O的半径为r,当点在圆外时,由切割线定理得AB·AC=64=(10+r)(10-r),解得r=6,当点在圆内时,由相交弦定理得AB·AC=64=(r+10)(r-10),解得r=2.
答案 C
3.如图所示,⊙O的割线PAB交⊙O于A,B两点,割线PCD经过圆心,已知PA=6,AB=7,PO=12,则⊙O的半径为
A.8 B.2
C.6 D.
解析 设圆的半径为r,根据割线定理,
得PA·PB=PC·PD,
即6×=(12-r)(12+r),解得r=8.
答案 A
4.如图所示,AB是⊙O的直径,BC是⊙O的切线,AC交⊙O于点D,若AD=32,CD=18,则AB的长为
A.1 600 B.40
C.4 D.96
解析 连接BD,则BD⊥AC,由射影定理,知AB2=AD×AC=32×50=1 600,故AB=40.
答案 B
5.如图所示,过⊙O外一点P作一条直线与⊙O交于A,B两点.已知PA=2,点P到⊙O的切线长PT=4,则弦AB的长为
A. B.8
C.6 D.16
解析 由圆的几何性质知PT2=PA·PB,∴PB=8,又PA=2,∴AB=6.
答案 C
6.如图,已知Rt△ABC的两条直角边AC,BC的长分别为3 cm,4 cm,以AC为直径的圆与AB交于点D,则等于
A.4 B.6
C.9 D.
解析 连接CD.
∵AC为⊙O的直径,∴CD⊥AD.
∵△ABC为直角三角形.
∴AC2=AD·AB,BC2=BD·AB,∴===.
答案 D
二、填空题
7.如图,已知在△ABC中,DE∥BC,DE分别与AB,AC相交于点D,E,AD∶AB=1∶3,若DE=2,则BC=________.
解析 ∵DE∥BC,∴=,∴BC=6.
答案 6
8.如图,已知PA、PB是圆O的切线,A、B分别为切点,C为圆O上不与A、B重合的另一点,若∠ACB=120°,则∠APB=________.
解析 连接OA、OB,∠PAO=∠PBO=90°,
∵∠ACB=120°,∴∠AOB=120°.
又P、A、O、B四点共圆,故∠APB=60°.
答案 60°
9.如图,点P在圆O直径AB的延长线上,且PB=OB=2,PC切圆O于C点,CD⊥AB于D点,则CD=________.
解析 由切割线定理知,
PC2=PA·PB,解得PC=2.
又OC⊥PC,故CD===.
答案
三、解答题
10.(2011·大连重点中学第二次联考)如图所示,AB是⊙O的直径,弦BD、CA的延长线相交于点E,EF垂直BA的延长线于点F.
求证:(1)∠DEA=∠DFA;
(2)AB2=BE·BD-AE·AC.
证明 (1)连接AD.
∵AB为⊙O的直径,
∴∠ADB=90°,即∠EDA=90°.
又EF⊥AB,∠EFA=90°,
则A、D、E、F四点共圆,∴∠DEA=∠DFA.
(2)由(1),知BD·BE=BA·BF,
又△ABC∽△AEF,∴=,
即AB·AF=AE·AC.
∴BE·BD-AE·AC=BA·BF-AB·AF=AB(BF-AF)=AB2.
11.如图,BD、CE是△ABC的高.求证:ADE∽△ABC.
证明 ∵BD、CE是△ABC的高,∴∠AEC=∠ADB=90°.
又∵∠A=∠A,∴△AEC∽△ADB,∴=.
又∵∠A=∠A,∴△ADE∽△ABC.
12.(2011·课标全国卷)如图,D,E分别为△ABC的边AB,AC上的点,且不与△ABC的顶点重合.已知AE的长为m,AC的长为n,AD,AB的长是关于x的方程x2-14x+mn=0的两个根.
(1)证明:C,B,D,E四点共圆;
(2)若∠A=90°,且m=4,n=6,求C,B,D,E所在圆的半径.
解析 (1)证明 如图,连接DE,在△ADE和△ACB中,AD·AB=mn=AE·AC,即=.又∠DAE=∠CAB,从而△ADE∽△ACB.
因此∠ADE=∠ACB.所以C,B,D,E四点共圆.
(2)m=4,n=6时,方程x2-14x+mn=0的两根为x1=2,x2=12.故AD=2,AB=12.
如图,取CE的中点G,DB的中点F,分别过G,F作AC,AB的垂线,两垂线相交于H点,连接DH.因为C,B,D,E四点共圆,所以C,B,D,E四点所在圆的圆心为H,半径为DH.
由于∠A=90°,故GH∥AB,HF∥AC.
从而HF=AG=5,DF=(12-2)=5.
故C,B,D,E四点所在圆的半径为5.
.精品资料。欢迎使用。 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
同课章节目录
