(导学教程)2012届高三数学(理)二轮复习试题:专题四第一讲综合验收评估(北师大版)
文档属性
| 名称 | (导学教程)2012届高三数学(理)二轮复习试题:专题四第一讲综合验收评估(北师大版) |  | |
| 格式 | zip | ||
| 文件大小 | 502.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-01 23:12:10 | ||
图片预览


文档简介
一、选择题
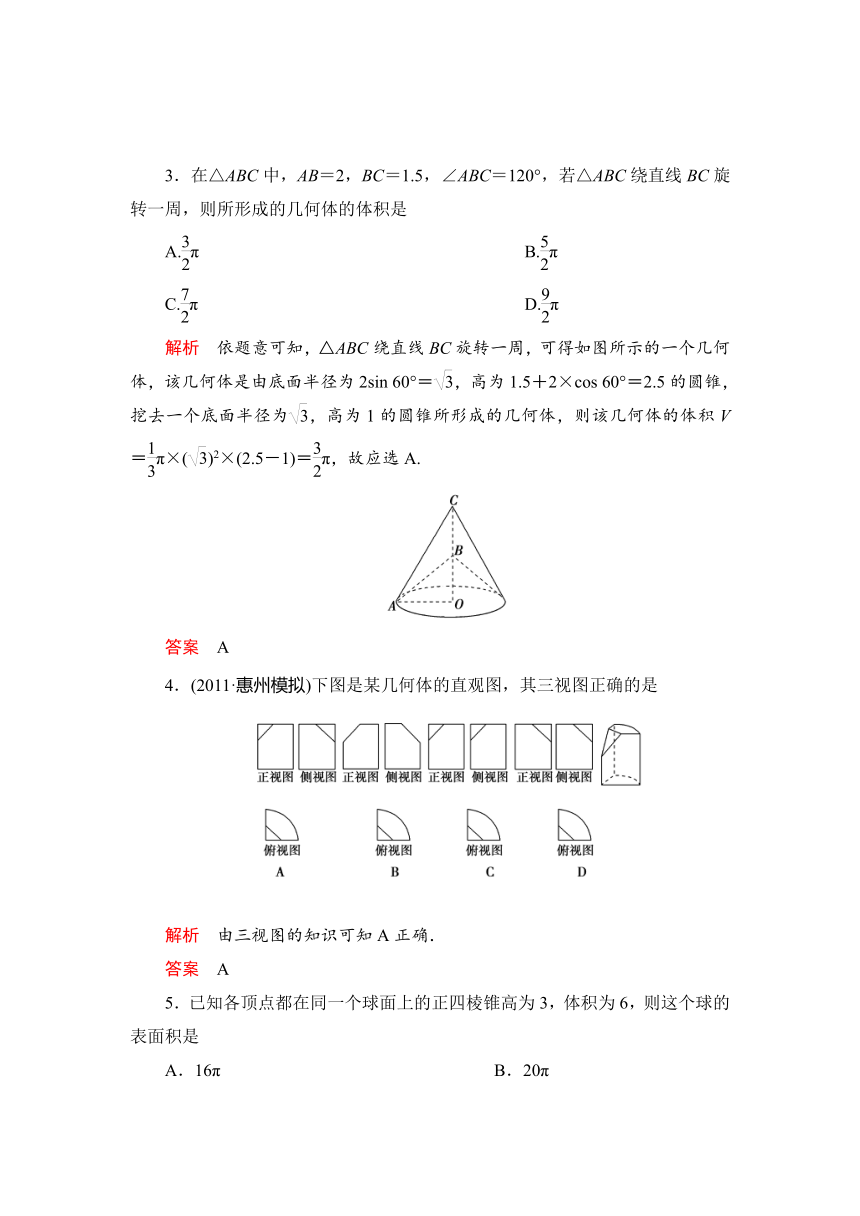
1.(2011·陕西)某几何体的三视图如下,则它的体积是
A.8- B.8-
C.8-2π D.
解析 由三视图可知该几何体是一个棱长为2的正方体内部挖去一个底面半径为1,高为2的圆锥,所以V=23-×π×2=8-,故选A.
答案 A
2.正方体ABCD-A1B1C1D1中,P、Q、E、F分别是AB、AD、B1C1、C1D1的中点,则正方体的过P、Q、E、F的截面图形的形状是
A.正方形 B.平行四边形
C.正五边形 D.正六边形
解析 如图所示,由EF∥PQ,可确定一个平面,
此平面与正方体的棱BB1、DD1分别相交于点M、N,
由此可得截面图形的形状为正六边形PQNFEM,故应选D.
答案 D
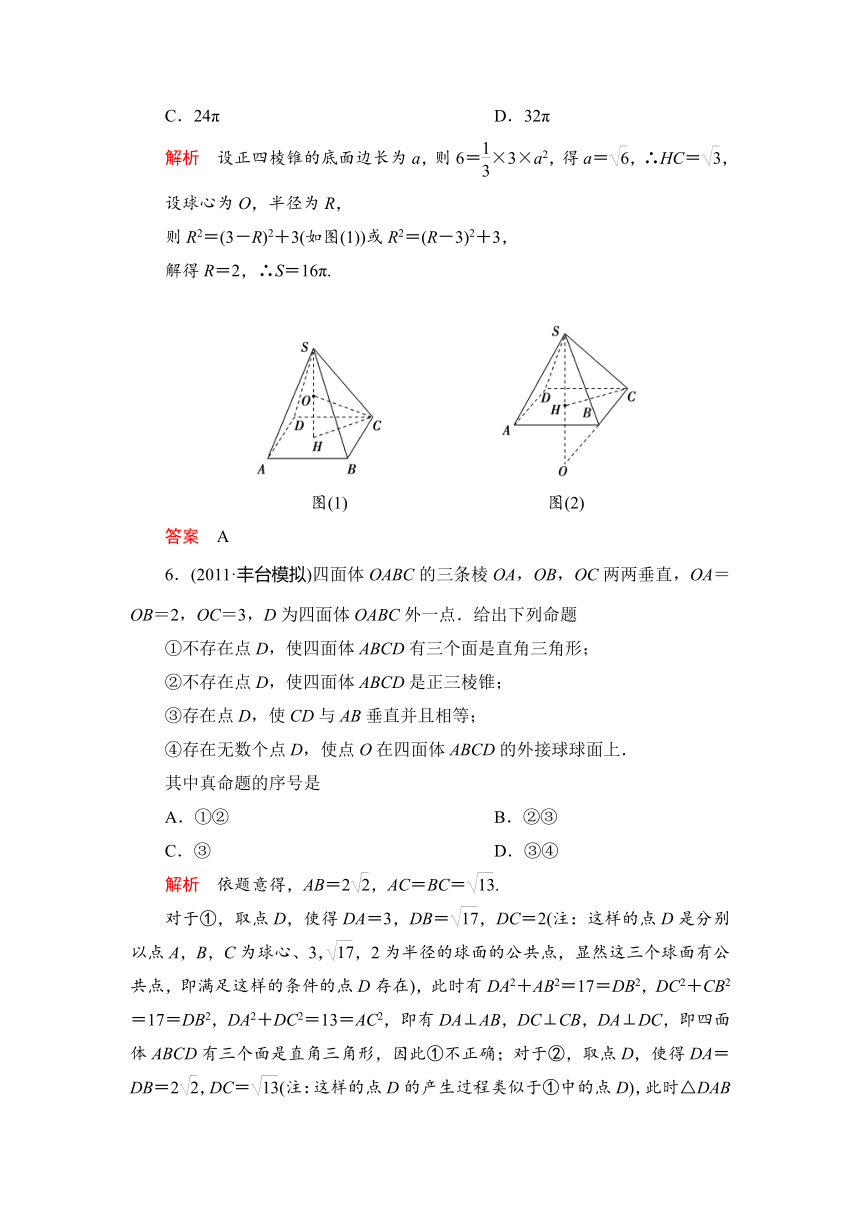
3.在△ABC中,AB=2,BC=1.5,∠ABC=120°,若△ABC绕直线BC旋转一周,则所形成的几何体的体积是
A.π B.π
C.π D.π
解析 依题意可知,△ABC绕直线BC旋转一周,可得如图所示的一个几何体,该几何体是由底面半径为2sin 60°=,高为1.5+2×cos 60°=2.5的圆锥,挖去一个底面半径为,高为1的圆锥所形成的几何体,则该几何体的体积V=π×()2×(2.5-1)=π,故应选A.
答案 A
4.(2011·惠州模拟)下图是某几何体的直观图,其三视图正确的是
解析 由三视图的知识可知A正确.
答案 A
5.已知各顶点都在同一个球面上的正四棱锥高为3,体积为6,则这个球的表面积是
A.16π B.20π
C.24π D.32π
解析 设正四棱锥的底面边长为a,则6=×3×a2,得a=,∴HC=,
设球心为O,半径为R,
则R2=(3-R)2+3(如图(1))或R2=(R-3)2+3,
解得R=2,∴S=16π.
图(1) 图(2)
答案 A
6.(2011·丰台模拟)四面体OABC的三条棱OA,OB,OC两两垂直,OA=OB=2,OC=3,D为四面体OABC外一点.给出下列命题
①不存在点D,使四面体ABCD有三个面是直角三角形;
②不存在点D,使四面体ABCD是正三棱锥;
③存在点D,使CD与AB垂直并且相等;
④存在无数个点D,使点O在四面体ABCD的外接球球面上.
其中真命题的序号是
A.①② B.②③
C.③ D.③④
解析 依题意得,AB=2,AC=BC=.
对于①,取点D,使得DA=3,DB=,DC=2(注:这样的点D是分别以点A,B,C为球心、3,,2为半径的球面的公共点,显然这三个球面有公共点,即满足这样的条件的点D存在),此时有DA2+AB2=17=DB2,DC2+CB2=17=DB2,DA2+DC2=13=AC2,即有DA⊥AB,DC⊥CB,DA⊥DC,即四面体ABCD有三个面是直角三角形,因此①不正确;对于②,取点D,使得DA=DB=2,DC=(注:这样的点D的产生过程类似于①中的点D),此时△DAB是等边三角形,三条侧棱相等,四面体ABCD,即C-ABD是正三棱锥,因此②不正确;对于③,将该四面体补成一个正四棱柱,易知取上底面的与点C相对的顶点作为点D,此时CD与AB垂直并且相等,因此③正确;对于④,将该四面体补成一个正四棱柱,作出该正四棱柱的外接球,在这个球面上任取一点(异于点A,B,C,O)作为点D都能满足点O在四面体ABCD的外接球球面上,因此④正确.综上所述,其中真命题的序号是③④,选D.
答案 D
二、填空题
7.(2011·福建)三棱锥P-ABC中,PA⊥底面ABC,PA=3,底面ABC是边长为2的正三角形,则三棱锥P-ABC的体积等于________.
解析 ∵PA⊥底面ABC,∴PA为三棱锥P-ABC的高,且PA=3.
∵底面ABC为正三角形且边长为2,
∴底面面积为×22×sin 60°=,
∴VP-ABC=××3=.
答案
8.一个正三棱柱的侧棱长和底面边长相等,体积为2,它的三视图中的俯视图如图所示,左视图是一个矩形,则这个矩形的面积是________.
解析 设底面边长为x,则V=x2·x=2,∴x=2.由题意知这个正三棱柱的左视图为长为2,宽为的矩形,其面积为2.
答案 2
9.如图,半径为4的球O中有一内接圆柱,当圆柱的侧面积最大时,球的表面积与该圆柱的侧面积之差是________.
解析 解法一 圆柱的轴截面如图所示,设球的半径与圆柱的高所成的角为α,则圆柱底面半径为4sin α,高为8cos α,∴S圆柱侧=2π·4sin α·8cos α=32πsin 2α.
∴当sin 2α=1时,S圆柱侧最大为32π.
此时S球表-S圆柱侧=4π·42-32π=32π.
解法二 设圆柱底面半径为r,则其高为2,
∴S圆柱侧=2πr·2=4π
≤4π=2πR2
.
又R=4,∴S圆柱侧最大为32π.
此时S球表-S圆柱侧=4π·42-32π=32π.
答案 32π
三、解答题
10.如图所示,在单位正方体ABCD-A1B1C1D1的面对角线A1B上存在一点P,使AP+D1P最短,求AP+D1P的最小值.
解析 设A1P=x,则
在△AA1P中,AP=
=,
在Rt△D1A1P中,D1P=.
∴y=AP+D1P=+,
下面求对应的函数y的最小值.
将函数y变形,得y= +,
它表示平面直角坐标系中,在x轴上存在一点P(x,0),
它到点M与到点N(0,-1)的距离之和最小,
∴当P、M、N三点共线时,这个值最小,
则为 =.
11.如图所示,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,PD⊥底面ABCD,且PD=a,PA=PC=a,若在这个四棱锥内放一球.求此球的最大半径.
解析 设放入的球的半径为r,球心为O,连接OP、OA、OB、OC、OD,
则把此四棱锥分割成四个三棱锥和一个四棱锥,
这些小棱锥的高都是r,
底面分别为原四棱锥的侧面和底面,
则VP-ABCD=r(S△PAB+S△PBC+S△PCD+S△PAD+S正方形ABCD)=r(2+)a2.
由题意,知PD⊥底面ABCD,
∴VP-ABCD=S正方形ABCD·PD=a3.
由体积相等,得r(2+)a2=a3,
解得r=(2-)a.
12.如图1,在三棱锥P-ABC中,PA⊥平面ABC,AC⊥BC,D为侧棱PC上一点,它的正(主)视图和侧(左)视图如图2所示.
(1)证明:AD⊥平面PBC;
(2)求三棱锥D-ABC的体积;
(3)在∠ACB的平分线上确定一点Q,使得PQ∥平面ABD,并求此时PQ的长.
解析 (1)证明 因为PA⊥平面ABC,所以PA⊥BC,
又AC⊥BC,所以BC⊥平面PAC,所以BC⊥AD.
由三视图可得,在△PAC中,PA=AC=4,
D为PC的中点,所以AD⊥PC,
所以AD⊥平面PBC.
(2)由三视图可得BC=4,
由(1)知∠ADC=90°,BC⊥平面PAC,
又三棱锥D-ABC的体积即为三棱锥B-ADC的体积,
所以所求三棱锥的体积V=××AD×CD×BC
=××2×2×4=.
(3)取AB的中点O,连接CO并延长至Q,使得CQ=2CO,
连接PQ,OD,点Q即为所求.
因为O为CQ的中点,D为PC的中点,
所以PQ∥OD,
因为PQ 平面ABD,OD 平面ABD,
所以PQ∥平面ABD,
连接AQ,BQ,因为四边形ACBQ的对角线互相平分,
且AC=BC,AC⊥BC,
所以四边形ACBQ为正方形,
所以,CQ即为∠ACB的平分线,
又AQ=4,PA⊥平面ABC,
所以在Rt△PAQ中,PQ==4.
.精品资料。欢迎使用。 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
1.(2011·陕西)某几何体的三视图如下,则它的体积是
A.8- B.8-
C.8-2π D.
解析 由三视图可知该几何体是一个棱长为2的正方体内部挖去一个底面半径为1,高为2的圆锥,所以V=23-×π×2=8-,故选A.
答案 A
2.正方体ABCD-A1B1C1D1中,P、Q、E、F分别是AB、AD、B1C1、C1D1的中点,则正方体的过P、Q、E、F的截面图形的形状是
A.正方形 B.平行四边形
C.正五边形 D.正六边形
解析 如图所示,由EF∥PQ,可确定一个平面,
此平面与正方体的棱BB1、DD1分别相交于点M、N,
由此可得截面图形的形状为正六边形PQNFEM,故应选D.
答案 D
3.在△ABC中,AB=2,BC=1.5,∠ABC=120°,若△ABC绕直线BC旋转一周,则所形成的几何体的体积是
A.π B.π
C.π D.π
解析 依题意可知,△ABC绕直线BC旋转一周,可得如图所示的一个几何体,该几何体是由底面半径为2sin 60°=,高为1.5+2×cos 60°=2.5的圆锥,挖去一个底面半径为,高为1的圆锥所形成的几何体,则该几何体的体积V=π×()2×(2.5-1)=π,故应选A.
答案 A
4.(2011·惠州模拟)下图是某几何体的直观图,其三视图正确的是
解析 由三视图的知识可知A正确.
答案 A
5.已知各顶点都在同一个球面上的正四棱锥高为3,体积为6,则这个球的表面积是
A.16π B.20π
C.24π D.32π
解析 设正四棱锥的底面边长为a,则6=×3×a2,得a=,∴HC=,
设球心为O,半径为R,
则R2=(3-R)2+3(如图(1))或R2=(R-3)2+3,
解得R=2,∴S=16π.
图(1) 图(2)
答案 A
6.(2011·丰台模拟)四面体OABC的三条棱OA,OB,OC两两垂直,OA=OB=2,OC=3,D为四面体OABC外一点.给出下列命题
①不存在点D,使四面体ABCD有三个面是直角三角形;
②不存在点D,使四面体ABCD是正三棱锥;
③存在点D,使CD与AB垂直并且相等;
④存在无数个点D,使点O在四面体ABCD的外接球球面上.
其中真命题的序号是
A.①② B.②③
C.③ D.③④
解析 依题意得,AB=2,AC=BC=.
对于①,取点D,使得DA=3,DB=,DC=2(注:这样的点D是分别以点A,B,C为球心、3,,2为半径的球面的公共点,显然这三个球面有公共点,即满足这样的条件的点D存在),此时有DA2+AB2=17=DB2,DC2+CB2=17=DB2,DA2+DC2=13=AC2,即有DA⊥AB,DC⊥CB,DA⊥DC,即四面体ABCD有三个面是直角三角形,因此①不正确;对于②,取点D,使得DA=DB=2,DC=(注:这样的点D的产生过程类似于①中的点D),此时△DAB是等边三角形,三条侧棱相等,四面体ABCD,即C-ABD是正三棱锥,因此②不正确;对于③,将该四面体补成一个正四棱柱,易知取上底面的与点C相对的顶点作为点D,此时CD与AB垂直并且相等,因此③正确;对于④,将该四面体补成一个正四棱柱,作出该正四棱柱的外接球,在这个球面上任取一点(异于点A,B,C,O)作为点D都能满足点O在四面体ABCD的外接球球面上,因此④正确.综上所述,其中真命题的序号是③④,选D.
答案 D
二、填空题
7.(2011·福建)三棱锥P-ABC中,PA⊥底面ABC,PA=3,底面ABC是边长为2的正三角形,则三棱锥P-ABC的体积等于________.
解析 ∵PA⊥底面ABC,∴PA为三棱锥P-ABC的高,且PA=3.
∵底面ABC为正三角形且边长为2,
∴底面面积为×22×sin 60°=,
∴VP-ABC=××3=.
答案
8.一个正三棱柱的侧棱长和底面边长相等,体积为2,它的三视图中的俯视图如图所示,左视图是一个矩形,则这个矩形的面积是________.
解析 设底面边长为x,则V=x2·x=2,∴x=2.由题意知这个正三棱柱的左视图为长为2,宽为的矩形,其面积为2.
答案 2
9.如图,半径为4的球O中有一内接圆柱,当圆柱的侧面积最大时,球的表面积与该圆柱的侧面积之差是________.
解析 解法一 圆柱的轴截面如图所示,设球的半径与圆柱的高所成的角为α,则圆柱底面半径为4sin α,高为8cos α,∴S圆柱侧=2π·4sin α·8cos α=32πsin 2α.
∴当sin 2α=1时,S圆柱侧最大为32π.
此时S球表-S圆柱侧=4π·42-32π=32π.
解法二 设圆柱底面半径为r,则其高为2,
∴S圆柱侧=2πr·2=4π
≤4π=2πR2
.
又R=4,∴S圆柱侧最大为32π.
此时S球表-S圆柱侧=4π·42-32π=32π.
答案 32π
三、解答题
10.如图所示,在单位正方体ABCD-A1B1C1D1的面对角线A1B上存在一点P,使AP+D1P最短,求AP+D1P的最小值.
解析 设A1P=x,则
在△AA1P中,AP=
=,
在Rt△D1A1P中,D1P=.
∴y=AP+D1P=+,
下面求对应的函数y的最小值.
将函数y变形,得y= +,
它表示平面直角坐标系中,在x轴上存在一点P(x,0),
它到点M与到点N(0,-1)的距离之和最小,
∴当P、M、N三点共线时,这个值最小,
则为 =.
11.如图所示,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,PD⊥底面ABCD,且PD=a,PA=PC=a,若在这个四棱锥内放一球.求此球的最大半径.
解析 设放入的球的半径为r,球心为O,连接OP、OA、OB、OC、OD,
则把此四棱锥分割成四个三棱锥和一个四棱锥,
这些小棱锥的高都是r,
底面分别为原四棱锥的侧面和底面,
则VP-ABCD=r(S△PAB+S△PBC+S△PCD+S△PAD+S正方形ABCD)=r(2+)a2.
由题意,知PD⊥底面ABCD,
∴VP-ABCD=S正方形ABCD·PD=a3.
由体积相等,得r(2+)a2=a3,
解得r=(2-)a.
12.如图1,在三棱锥P-ABC中,PA⊥平面ABC,AC⊥BC,D为侧棱PC上一点,它的正(主)视图和侧(左)视图如图2所示.
(1)证明:AD⊥平面PBC;
(2)求三棱锥D-ABC的体积;
(3)在∠ACB的平分线上确定一点Q,使得PQ∥平面ABD,并求此时PQ的长.
解析 (1)证明 因为PA⊥平面ABC,所以PA⊥BC,
又AC⊥BC,所以BC⊥平面PAC,所以BC⊥AD.
由三视图可得,在△PAC中,PA=AC=4,
D为PC的中点,所以AD⊥PC,
所以AD⊥平面PBC.
(2)由三视图可得BC=4,
由(1)知∠ADC=90°,BC⊥平面PAC,
又三棱锥D-ABC的体积即为三棱锥B-ADC的体积,
所以所求三棱锥的体积V=××AD×CD×BC
=××2×2×4=.
(3)取AB的中点O,连接CO并延长至Q,使得CQ=2CO,
连接PQ,OD,点Q即为所求.
因为O为CQ的中点,D为PC的中点,
所以PQ∥OD,
因为PQ 平面ABD,OD 平面ABD,
所以PQ∥平面ABD,
连接AQ,BQ,因为四边形ACBQ的对角线互相平分,
且AC=BC,AC⊥BC,
所以四边形ACBQ为正方形,
所以,CQ即为∠ACB的平分线,
又AQ=4,PA⊥平面ABC,
所以在Rt△PAQ中,PQ==4.
.精品资料。欢迎使用。 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
同课章节目录
