(导学教程)2012届高三数学(理)二轮复习试题:专题五第三讲综合验收评估(北师大版)
文档属性
| 名称 | (导学教程)2012届高三数学(理)二轮复习试题:专题五第三讲综合验收评估(北师大版) |  | |
| 格式 | zip | ||
| 文件大小 | 330.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-01 23:12:20 | ||
图片预览



文档简介
一、选择题
1.以椭圆+=1内的点M(1,1)为中点的弦所在直线的方程为
A.4x-y-3=0 B.x-4y+3=0
C.4x+y-5=0 D.x+4y-5=0
解析 设弦的两个端点坐标分别为(x1,y1),(x2,y2),
则有+=1,①
+=1.②
②-①得+=0,
整理得=-·=-×=-,
即斜率k=-,
所以所求直线方程为y-1=-(x-1),
整理得x+4y-5=0.
答案 D
2.已知椭圆+=1,若此椭圆上存在不同的两点A、B关于直线y=4x+m对称,则实数m的取值范围是
A. B.
C. D.
解析 设A(x1,y1),B(x2,y2),AB的中点M(x,y),kAB==-,
x1+x2=2x,y1+y2=2y,3x+4y=12①
3x+4y=12②
①②两式相减得3(x-x)+4(y-y)=0,
即y1+y2=3(x1+x2),
即y=3x,与y=4x+m联立得x=-m,y=-3m,
而M(x,y)在椭圆的内部,
则+<1,即-<m<.
答案 B
3.(2011·四平模拟)在y=2x2上有一点P,它到A(1,3)的距离与它到焦点的距离之和最小,则点P的坐标是
A.(-2,1) B.(1,2)
C.(2,1) D.(-1,2)
解析 如图所示,直线l为抛物线y=2x2的准线,F为其焦点,
PN⊥l,AN1⊥l,由抛物线的定义知,|PF|=|PN|,
∴|AP|+|PF|=|AP|+|PN|≥|AN1|,
当且仅当A、P、N三点共线时取等号.
∴P点的横坐标与A点的横坐标相同即为1,
则可排除A、C、D,故选B.
答案 B
4.已知双曲线-=1(a>0,b>0)的右焦点为F,若过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是
A.[1,2] B.(1,2)
C.[2,+∞) D.(2,+∞)
解析 因为双曲线-=1(a>0,b>0)的右焦点为F,过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点,所以该直线的斜率的绝对值小于等于此双曲线渐近线的斜率的绝对值,即≥.因为e2==,所以e≥2,故选C.
答案 C
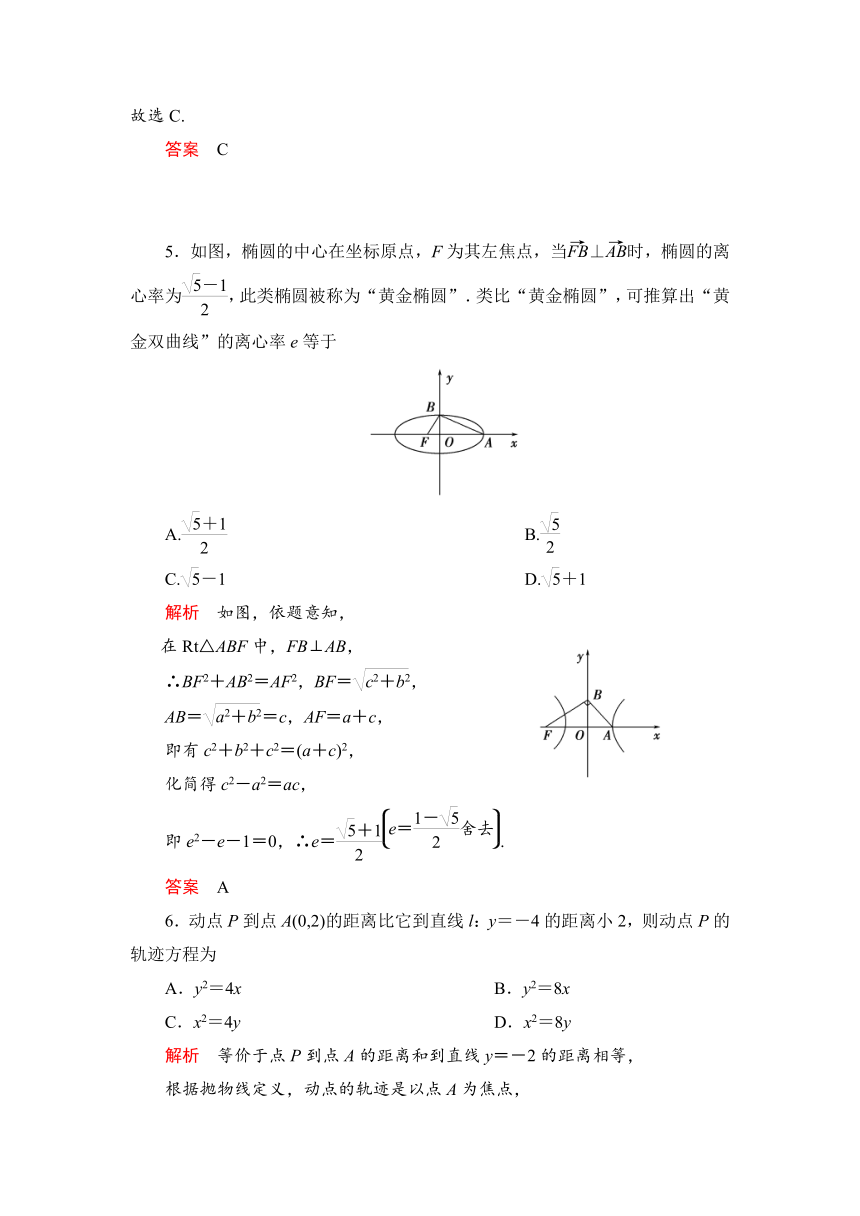
5.如图,椭圆的中心在坐标原点,F为其左焦点,当⊥时,椭圆的离心率为,此类椭圆被称为“黄金椭圆”.类比“黄金椭圆”,可推算出“黄金双曲线”的离心率e等于
A. B.
C.-1 D.+1
解析 如图,依题意知,
在Rt△ABF中,FB⊥AB,
∴BF2+AB2=AF2,BF=,
AB==c,AF=a+c,
即有c2+b2+c2=(a+c)2,
化简得c2-a2=ac,
即e2-e-1=0,∴e=.
答案 A
6.动点P到点A(0,2)的距离比它到直线l:y=-4的距离小2,则动点P的轨迹方程为
A.y2=4x B.y2=8x
C.x2=4y D.x2=8y
解析 等价于点P到点A的距离和到直线y=-2的距离相等,
根据抛物线定义,动点的轨迹是以点A为焦点,
直线y=-2为准线的抛物线,焦参数p=4,
故所求的抛物线方程为x2=8y.
答案 D
二、填空题
7.若双曲线-=1(a>0,b>0)的一条渐近线的倾斜角为60°,则的最小值是________.
解析 根据=,即b=a,
∴==3a+≥2,
当且仅当3a=,即a=时等号成立.
答案 2
8.(2011·南昌模拟)已知点F(1,0),直线l:x=-1,P为平面上的动点,过P作直线l的垂线,垂足为点Q,且·=·,则动点P的轨迹C的方程是________.
解析 设点P(x,y),则Q(-1,y),
由·=·,得
(x+1,0)·(2,-y)=(x-1,y)·(-2,y),
化简,得y2=4x.故填y2=4x.
答案 y2=4x
9.已知曲线-=1与直线x+y-1=0相交于P、Q两点,且·=0(O为原点),则-的值为________.
解析 将y=1-x代入-=1,
得(b-a)x2+2ax-(a+ab)=0.
设P(x1,y1),Q(x2,y2),
则x1+x2=,x1x2=.
·=x1x2+y1y2=x1x2+(1-x1)(1-x2)
=2x1x2-(x1+x2)+1.
所以-+1=0,即2a+2ab-2a+a-b=0,
即b-a=2ab,所以-=2.
答案 2
三、解答题
10.(2011·天津)在平面直角坐标系xOy中,点P(a,b)(a>b>0)为动点,F1,F2分别为椭圆+=1的左,右焦点.已知△F1PF2为等腰三角形.
(1)求椭圆的离心率e;
(2)设直线PF2与椭圆相交于A,B两点,M是直线PF2上的点,满足·=-2,求点M的轨迹方程.
解析 (1)设F1(-c,0),F2(c,0)(c>0).
由题意,可得|PF2|=|F1F2|,即=2c,
整理得22+-1=0,
得=-1(舍去)或=.所以e=.
(2)由(1)知a=2c,b=c,可得椭圆方程为3x2+4y2=12c2,直线PF2的方程为y=(x-c).
A,B两点的坐标满足方程组消去y并整理,得5x2-8cx=0.解得x1=0,x2=c,得方程组的解
不妨设A,B(0,-c).
设点M的坐标为(x,y),则=,
=(x,y+c).
由y=(x-c),得c=x-y.
于是=,=(x,x).
由·=-2,
即·x+·x=-2,
化简得18x2-16xy-15=0.
将y=代入c=x-y,得c=>0.
所以x>0.
因此,点M的轨迹方程是18x2-16xy-15=0(x>0).
11.如图所示,椭圆+=1(a>b>0)和圆O:x2+y2=b2,过椭圆上一点P引圆O的两条切线,切点分别为A、B.
(1)①若圆O过椭圆的两个焦点,求椭圆的离心率e;
②若椭圆上存在点P,使得∠APB=90°,求椭圆离心率e的取值范围.
(2)设直线AB与x轴,y轴分别交于点M,N,求证:+为定值.
解析 (1)①∵圆O过椭圆的焦点,圆O:x2+y2=b2,∴b=c,∴a2=2c2,∴e=.
②由∠APB=90°及圆的性质,可得|OP|=b,
∴|OP|2=2b2≤a2,∴a2≤2c2,
∴e2≥,即≤e<1.
(2)证明 设P(x0,y0),A(x1,y1),B(x2,y2).
由PA⊥OA得=-,
整理得x0x1+y0y1=x+y,
∵x+y=b2,∴PA的方程为x1x+y1y=b2.
同理PB的方程为x2x+y2y=b2.
PA、PB都过点P(x0,y0),
∴x1x0+y1y0=b2且x2x0+y2y0=b2,
∴直线AB的方程为x0x+y0y=b2.
令x=0,得|ON|=|y|=,
令y=0,得|OM|=|x|=,
∴+===.
∴+为定值,定值是.
12.已知两点M(-2,0),N(2,0),点P为坐标平面内的动点,且满足||||+·=0.
(1)求点P的轨迹C的方程;
(2)设过点N的直线l斜率为k,且与曲线C相交于点S、T,若S、T两点只在第二象限内运动,线段ST的垂直平分线交x轴于Q点,求Q点横坐标的取值范围.
解析 (1)设点P(x,y),根据题意则有:
=(4,0),||=4,||=,=(x-2,y),
代入||||+·=0得4+4(x-2)=0,
整理得点P的轨迹C的方程y2=-8x.
(2)设S(x1,y1),T(x2,y2),
由题意得ST的方程为y=k(x-2)(显然k≠0),与y2=-8x联立消元得ky2+8y+16k=0,
则有y1+y2=-,y1y2=16,
因为直线l交轨迹C于两点,则Δ=64-64k2>0,
再由y1>0,y2>0,则->0,故-1<k<0,
可求得线段ST中点B的坐标为,
所以线段ST的垂直平分线方程为y+
=-,
令y=0得点Q的横坐标为xQ=-2-<-6,
所以Q点横坐标的取值范围为(-∞,-6).
.精品资料。欢迎使用。 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
1.以椭圆+=1内的点M(1,1)为中点的弦所在直线的方程为
A.4x-y-3=0 B.x-4y+3=0
C.4x+y-5=0 D.x+4y-5=0
解析 设弦的两个端点坐标分别为(x1,y1),(x2,y2),
则有+=1,①
+=1.②
②-①得+=0,
整理得=-·=-×=-,
即斜率k=-,
所以所求直线方程为y-1=-(x-1),
整理得x+4y-5=0.
答案 D
2.已知椭圆+=1,若此椭圆上存在不同的两点A、B关于直线y=4x+m对称,则实数m的取值范围是
A. B.
C. D.
解析 设A(x1,y1),B(x2,y2),AB的中点M(x,y),kAB==-,
x1+x2=2x,y1+y2=2y,3x+4y=12①
3x+4y=12②
①②两式相减得3(x-x)+4(y-y)=0,
即y1+y2=3(x1+x2),
即y=3x,与y=4x+m联立得x=-m,y=-3m,
而M(x,y)在椭圆的内部,
则+<1,即-<m<.
答案 B
3.(2011·四平模拟)在y=2x2上有一点P,它到A(1,3)的距离与它到焦点的距离之和最小,则点P的坐标是
A.(-2,1) B.(1,2)
C.(2,1) D.(-1,2)
解析 如图所示,直线l为抛物线y=2x2的准线,F为其焦点,
PN⊥l,AN1⊥l,由抛物线的定义知,|PF|=|PN|,
∴|AP|+|PF|=|AP|+|PN|≥|AN1|,
当且仅当A、P、N三点共线时取等号.
∴P点的横坐标与A点的横坐标相同即为1,
则可排除A、C、D,故选B.
答案 B
4.已知双曲线-=1(a>0,b>0)的右焦点为F,若过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是
A.[1,2] B.(1,2)
C.[2,+∞) D.(2,+∞)
解析 因为双曲线-=1(a>0,b>0)的右焦点为F,过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点,所以该直线的斜率的绝对值小于等于此双曲线渐近线的斜率的绝对值,即≥.因为e2==,所以e≥2,故选C.
答案 C
5.如图,椭圆的中心在坐标原点,F为其左焦点,当⊥时,椭圆的离心率为,此类椭圆被称为“黄金椭圆”.类比“黄金椭圆”,可推算出“黄金双曲线”的离心率e等于
A. B.
C.-1 D.+1
解析 如图,依题意知,
在Rt△ABF中,FB⊥AB,
∴BF2+AB2=AF2,BF=,
AB==c,AF=a+c,
即有c2+b2+c2=(a+c)2,
化简得c2-a2=ac,
即e2-e-1=0,∴e=.
答案 A
6.动点P到点A(0,2)的距离比它到直线l:y=-4的距离小2,则动点P的轨迹方程为
A.y2=4x B.y2=8x
C.x2=4y D.x2=8y
解析 等价于点P到点A的距离和到直线y=-2的距离相等,
根据抛物线定义,动点的轨迹是以点A为焦点,
直线y=-2为准线的抛物线,焦参数p=4,
故所求的抛物线方程为x2=8y.
答案 D
二、填空题
7.若双曲线-=1(a>0,b>0)的一条渐近线的倾斜角为60°,则的最小值是________.
解析 根据=,即b=a,
∴==3a+≥2,
当且仅当3a=,即a=时等号成立.
答案 2
8.(2011·南昌模拟)已知点F(1,0),直线l:x=-1,P为平面上的动点,过P作直线l的垂线,垂足为点Q,且·=·,则动点P的轨迹C的方程是________.
解析 设点P(x,y),则Q(-1,y),
由·=·,得
(x+1,0)·(2,-y)=(x-1,y)·(-2,y),
化简,得y2=4x.故填y2=4x.
答案 y2=4x
9.已知曲线-=1与直线x+y-1=0相交于P、Q两点,且·=0(O为原点),则-的值为________.
解析 将y=1-x代入-=1,
得(b-a)x2+2ax-(a+ab)=0.
设P(x1,y1),Q(x2,y2),
则x1+x2=,x1x2=.
·=x1x2+y1y2=x1x2+(1-x1)(1-x2)
=2x1x2-(x1+x2)+1.
所以-+1=0,即2a+2ab-2a+a-b=0,
即b-a=2ab,所以-=2.
答案 2
三、解答题
10.(2011·天津)在平面直角坐标系xOy中,点P(a,b)(a>b>0)为动点,F1,F2分别为椭圆+=1的左,右焦点.已知△F1PF2为等腰三角形.
(1)求椭圆的离心率e;
(2)设直线PF2与椭圆相交于A,B两点,M是直线PF2上的点,满足·=-2,求点M的轨迹方程.
解析 (1)设F1(-c,0),F2(c,0)(c>0).
由题意,可得|PF2|=|F1F2|,即=2c,
整理得22+-1=0,
得=-1(舍去)或=.所以e=.
(2)由(1)知a=2c,b=c,可得椭圆方程为3x2+4y2=12c2,直线PF2的方程为y=(x-c).
A,B两点的坐标满足方程组消去y并整理,得5x2-8cx=0.解得x1=0,x2=c,得方程组的解
不妨设A,B(0,-c).
设点M的坐标为(x,y),则=,
=(x,y+c).
由y=(x-c),得c=x-y.
于是=,=(x,x).
由·=-2,
即·x+·x=-2,
化简得18x2-16xy-15=0.
将y=代入c=x-y,得c=>0.
所以x>0.
因此,点M的轨迹方程是18x2-16xy-15=0(x>0).
11.如图所示,椭圆+=1(a>b>0)和圆O:x2+y2=b2,过椭圆上一点P引圆O的两条切线,切点分别为A、B.
(1)①若圆O过椭圆的两个焦点,求椭圆的离心率e;
②若椭圆上存在点P,使得∠APB=90°,求椭圆离心率e的取值范围.
(2)设直线AB与x轴,y轴分别交于点M,N,求证:+为定值.
解析 (1)①∵圆O过椭圆的焦点,圆O:x2+y2=b2,∴b=c,∴a2=2c2,∴e=.
②由∠APB=90°及圆的性质,可得|OP|=b,
∴|OP|2=2b2≤a2,∴a2≤2c2,
∴e2≥,即≤e<1.
(2)证明 设P(x0,y0),A(x1,y1),B(x2,y2).
由PA⊥OA得=-,
整理得x0x1+y0y1=x+y,
∵x+y=b2,∴PA的方程为x1x+y1y=b2.
同理PB的方程为x2x+y2y=b2.
PA、PB都过点P(x0,y0),
∴x1x0+y1y0=b2且x2x0+y2y0=b2,
∴直线AB的方程为x0x+y0y=b2.
令x=0,得|ON|=|y|=,
令y=0,得|OM|=|x|=,
∴+===.
∴+为定值,定值是.
12.已知两点M(-2,0),N(2,0),点P为坐标平面内的动点,且满足||||+·=0.
(1)求点P的轨迹C的方程;
(2)设过点N的直线l斜率为k,且与曲线C相交于点S、T,若S、T两点只在第二象限内运动,线段ST的垂直平分线交x轴于Q点,求Q点横坐标的取值范围.
解析 (1)设点P(x,y),根据题意则有:
=(4,0),||=4,||=,=(x-2,y),
代入||||+·=0得4+4(x-2)=0,
整理得点P的轨迹C的方程y2=-8x.
(2)设S(x1,y1),T(x2,y2),
由题意得ST的方程为y=k(x-2)(显然k≠0),与y2=-8x联立消元得ky2+8y+16k=0,
则有y1+y2=-,y1y2=16,
因为直线l交轨迹C于两点,则Δ=64-64k2>0,
再由y1>0,y2>0,则->0,故-1<k<0,
可求得线段ST中点B的坐标为,
所以线段ST的垂直平分线方程为y+
=-,
令y=0得点Q的横坐标为xQ=-2-<-6,
所以Q点横坐标的取值范围为(-∞,-6).
.精品资料。欢迎使用。 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
同课章节目录
