(导学教程)2012届高三数学(理)二轮复习试题:专题一第四讲综合验收评估(北师大版)
文档属性
| 名称 | (导学教程)2012届高三数学(理)二轮复习试题:专题一第四讲综合验收评估(北师大版) |  | |
| 格式 | zip | ||
| 文件大小 | 388.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-01 23:12:38 | ||
图片预览



文档简介
一、选择题
1.f(x)=x(2 011+ln x),若f′(x0)=2 012,则x0等于
A.e2 B.1
C.ln 2 D.e
解析 f′(x)=2 011+ln x+x×=2 012+ln x,
故由f′(x0)=2 012,得2 012+ln x0=2 012,
所以ln x0=0,解得x0=1,故选B.
答案 B
2.(2011·湖南)曲线y=-在点M处的切线的斜率为
A.- B.
C.- D.
解析 y′==,
∴曲线在点M处的切线的斜率为.
答案 B
3.设函数f(x)=xm+ax的导函数f′(x)=2x+1,则f(-x)dx的值等于
A. B.
C. D.
解析 f′(x)=mxm-1+a=2x+1,
∴m=2,a=1,∴f(x)=x2+x,
f(-x)=x2-x,∴f(-x)dx=(x2-x)dx==,故选A.
答案 A
4.(2011·海淀模拟)已知点P在函数f(x)=acos x的图象上,则该函数图象在x=处的切线方程是
A.2x+y+=0 B.2x-y+=0
C.2x-y-=0 D.2x+y-=0
解析 由点P在函数f(x)的图象上,可得f=-1,
即acos =acos =-=-1,
解得a=2.故f(x)=2cos x.
所以f=2cos =-,f′(x)=-2sin x.
由导数的几何意义,可知该函数图象在x=处的切线斜率k=f′=-2sin =-.
所以切线方程为y-(-)=-,
即x+y+-=0,
也就是2x+y+=0,故选A.
答案 A
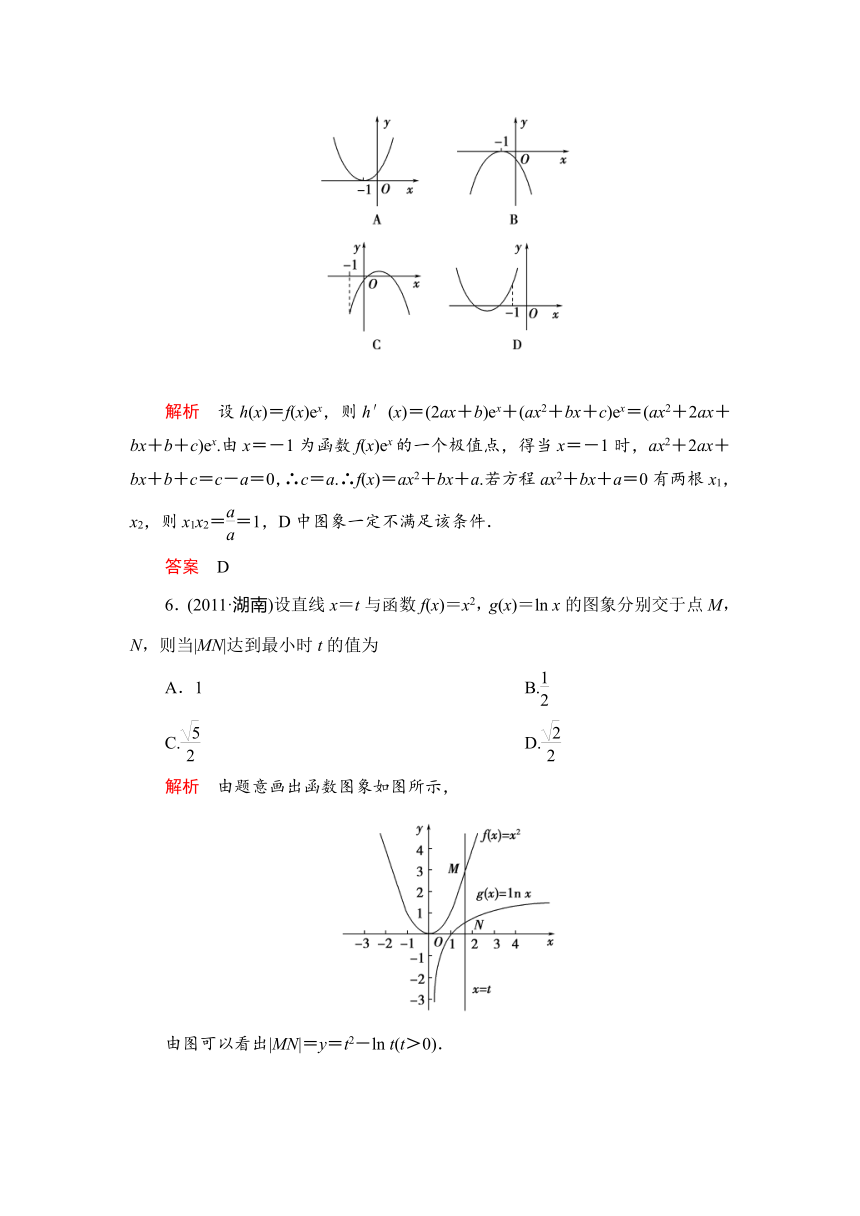
5.(2011·浙江模拟)设函数f(x)=ax2+bx+c(a,b,c∈R),若x=-1为函数f(x)ex的一个极值点,则下列图象不可能为y=f(x)图象的是
解析 设h(x)=f(x)ex,则h′(x)=(2ax+b)ex+(ax2+bx+c)ex=(ax2+2ax+bx+b+c)ex.由x=-1为函数f(x)ex的一个极值点,得当x=-1时,ax2+2ax+bx+b+c=c-a=0,∴c=a.∴f(x)=ax2+bx+a.若方程ax2+bx+a=0有两根x1,x2,则x1x2==1,D中图象一定不满足该条件.
答案 D
6.(2011·湖南)设直线x=t与函数f(x)=x2,g(x)=ln x的图象分别交于点M,N,则当|MN|达到最小时t的值为
A.1 B.
C. D.
解析 由题意画出函数图象如图所示,
由图可以看出|MN|=y=t2-ln t(t>0).
y′=2t-==.
当0<t<时,y′<0,可知y在此区间内单调递减;
当t>时,y′>0,可知y在此区间内单调递增.
故当t=时,|MN|有最小值.
答案 D
二、填空题
7.如图,直线y=1与曲线y=-x2+2所围图形的面积是________.
解析 令-x2+2=1,得x=±1,
答案
8.已知函数f(x)=mx2+ln x-2x在定义域内是增函数,则实数m的取值范围为________.
解析 当x>0时,f′(x)=mx+-2≥0恒成立,
即m≥-+恒成立,
又∵-+=-2+1≤1,∴m≥1.
答案 m≥1
9.函数f(x)=excos x的图象在点(0,f(0))处的切线的倾斜角为________.
解析 f′(x)=excos x+ex(-sin x),设切线的倾斜角为α,
则k=tan α=f′(0)=1,又α∈(0,π),∴α=.
答案
三、解答题
10.(2011·江苏)请你设计一个包装盒,如图所示,ABCD是边长为60 cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A,B,C,D四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E,F在AB上,是被切去的一个等腰直角三角形斜边的两个端点,设AE=FB=x(cm).
(1)某广告商要求包装盒的侧面积S(cm2)最大,试问x应取何值?
(2)某厂商要求包装盒的容积V(cm3)最大,试问x应取何值?并求出此时包装盒的高与底面边长的比值.
解析 设包装盒的高为h cm,底面边长为a cm.
由已知得a=x,h==(30-x),0<x<30.
(1)S=4ah=8x(30-x)=-8(x-15)2+1 800,
所以当x=15时,S取得最大值.
(2)V=a2h=2(-x3+30x2),V′=6x(20-x).
由V′=0,得x=0(舍)或x=20.
当x∈(0,20)时,V′>0;
当x∈(20,30)时,V′<0.
所以当x=20时,V取得极大值,也是最大值.
此时=.
即包装盒的高与底面边长的比值为.
11.已知函数f(x)=x2-3x+2ln x.
(1)求函数f(x)在[1,e]上的最大值和最小值;
(2)求证:在区间[1,+∞)上,函数f(x)的图象在函数g(x)=x3-3x图象的下方.
解析 (1)由f(x)=x2-3x+2ln x,知f′(x)=x+-3==.
当x∈(1,2)时,f′(x)<0,∴f(x)在[1,2]上是减函数;
当x∈(2,e)时,f′(x)>0,∴f(x)在[2,e]上是增函数.
∴当x=2时,f(x)min=f(2)=2ln 2-4.
又f(1)=-,f(e)=e2-3e+2,
f(e)-f(1)=e2-3e+2-
=(e2-6e+9)=(e-3)2>0,
∴f(e)>f(1),∴f(x)max=f(e)=e2-3e+2.
综上,函数f(x)在[1,e]上的最大值为e2-3e+2,最小值为2ln 2-4.
(2)证明 设F(x)=x2-3x+2ln x-x3+3x,
则F′(x)=-3x2+x+==.
当x∈(1,+∞)时,F′(x)<0,∴F(x)在[1,+∞)上是减函数,
且F(1)=-<0,故当x∈[1,+∞)时,F(x)<0,
∴x2-3x+2ln x<x3-3x.
∴在区间[1,+∞)上,函数f(x)的图象在函数g(x)=x3-3x图象的下方.
12.设f(x)=ex-1.
(1)当x>-1时,证明:f(x)>;
(2)当a>ln 2-1且x>0时,证明:f(x)>x2-2ax.
证明 (1)当x>-1时,f(x)>,
即ex-1>=2x-1,
故结论成立当且仅当ex>2x,即ex-2x>0.
令g(x)=ex-2x,则g′(x)=ex-2.
令g′(x)=0,即ex-2=0,解得x=ln 2.
当x∈(-1,ln 2)时,g′(x)=ex-2<0,
故函数g(x)在(-1,ln 2]上单调递减;
当x∈(ln 2,+∞)时,g′(x)=ex-2>0,
故函数g(x)在[ln 2,+∞)上单调递增.
所以g(x)在(-1,+∞)上的最小值为g(ln 2)=eln 2-2ln 2=2(1-ln 2)>0,
所以在(-1,+∞)上有g(x)≥g(ln 2)>0,即ex>2x.
故当x∈(-1,+∞)时,有f(x)>.
(2)f(x)>x2-2ax,即ex-1>x2-2ax,也就是ex-x2+2ax-1>0.
令g(x)=ex-x2+2ax-1,则g′(x)=ex-2x+2a.
令h(x)=ex-2x+2a,则h′(x)=ex-2.
由(1),可知当x∈(-∞,ln 2)时,h′(x)<0,函数h(x)单调递减;
当x∈(ln 2,+∞)时,h′(x)>0,函数h(x)单调递增.
所以h(x)的最小值为h(ln 2)=eln 2-2ln 2+2a=2-2ln 2+2a.
因为a>ln 2-1,所以h(ln 2)>2-2ln 2+2(ln 2-1)=0,
即h(x)≥h(ln 2)>0.
所以g′(x)=h(x)>0,即g(x)在R上为增函数.
故g(x)在(0,+∞)上为增函数,所以g(x)>g(0).
而g(0)=0,所以g(x)=ex-x2+2ax-1>0,
即当a>ln 2-1且x>0时,f(x)>x2-2ax.
.精品资料。欢迎使用。 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
1.f(x)=x(2 011+ln x),若f′(x0)=2 012,则x0等于
A.e2 B.1
C.ln 2 D.e
解析 f′(x)=2 011+ln x+x×=2 012+ln x,
故由f′(x0)=2 012,得2 012+ln x0=2 012,
所以ln x0=0,解得x0=1,故选B.
答案 B
2.(2011·湖南)曲线y=-在点M处的切线的斜率为
A.- B.
C.- D.
解析 y′==,
∴曲线在点M处的切线的斜率为.
答案 B
3.设函数f(x)=xm+ax的导函数f′(x)=2x+1,则f(-x)dx的值等于
A. B.
C. D.
解析 f′(x)=mxm-1+a=2x+1,
∴m=2,a=1,∴f(x)=x2+x,
f(-x)=x2-x,∴f(-x)dx=(x2-x)dx==,故选A.
答案 A
4.(2011·海淀模拟)已知点P在函数f(x)=acos x的图象上,则该函数图象在x=处的切线方程是
A.2x+y+=0 B.2x-y+=0
C.2x-y-=0 D.2x+y-=0
解析 由点P在函数f(x)的图象上,可得f=-1,
即acos =acos =-=-1,
解得a=2.故f(x)=2cos x.
所以f=2cos =-,f′(x)=-2sin x.
由导数的几何意义,可知该函数图象在x=处的切线斜率k=f′=-2sin =-.
所以切线方程为y-(-)=-,
即x+y+-=0,
也就是2x+y+=0,故选A.
答案 A
5.(2011·浙江模拟)设函数f(x)=ax2+bx+c(a,b,c∈R),若x=-1为函数f(x)ex的一个极值点,则下列图象不可能为y=f(x)图象的是
解析 设h(x)=f(x)ex,则h′(x)=(2ax+b)ex+(ax2+bx+c)ex=(ax2+2ax+bx+b+c)ex.由x=-1为函数f(x)ex的一个极值点,得当x=-1时,ax2+2ax+bx+b+c=c-a=0,∴c=a.∴f(x)=ax2+bx+a.若方程ax2+bx+a=0有两根x1,x2,则x1x2==1,D中图象一定不满足该条件.
答案 D
6.(2011·湖南)设直线x=t与函数f(x)=x2,g(x)=ln x的图象分别交于点M,N,则当|MN|达到最小时t的值为
A.1 B.
C. D.
解析 由题意画出函数图象如图所示,
由图可以看出|MN|=y=t2-ln t(t>0).
y′=2t-==.
当0<t<时,y′<0,可知y在此区间内单调递减;
当t>时,y′>0,可知y在此区间内单调递增.
故当t=时,|MN|有最小值.
答案 D
二、填空题
7.如图,直线y=1与曲线y=-x2+2所围图形的面积是________.
解析 令-x2+2=1,得x=±1,
答案
8.已知函数f(x)=mx2+ln x-2x在定义域内是增函数,则实数m的取值范围为________.
解析 当x>0时,f′(x)=mx+-2≥0恒成立,
即m≥-+恒成立,
又∵-+=-2+1≤1,∴m≥1.
答案 m≥1
9.函数f(x)=excos x的图象在点(0,f(0))处的切线的倾斜角为________.
解析 f′(x)=excos x+ex(-sin x),设切线的倾斜角为α,
则k=tan α=f′(0)=1,又α∈(0,π),∴α=.
答案
三、解答题
10.(2011·江苏)请你设计一个包装盒,如图所示,ABCD是边长为60 cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A,B,C,D四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E,F在AB上,是被切去的一个等腰直角三角形斜边的两个端点,设AE=FB=x(cm).
(1)某广告商要求包装盒的侧面积S(cm2)最大,试问x应取何值?
(2)某厂商要求包装盒的容积V(cm3)最大,试问x应取何值?并求出此时包装盒的高与底面边长的比值.
解析 设包装盒的高为h cm,底面边长为a cm.
由已知得a=x,h==(30-x),0<x<30.
(1)S=4ah=8x(30-x)=-8(x-15)2+1 800,
所以当x=15时,S取得最大值.
(2)V=a2h=2(-x3+30x2),V′=6x(20-x).
由V′=0,得x=0(舍)或x=20.
当x∈(0,20)时,V′>0;
当x∈(20,30)时,V′<0.
所以当x=20时,V取得极大值,也是最大值.
此时=.
即包装盒的高与底面边长的比值为.
11.已知函数f(x)=x2-3x+2ln x.
(1)求函数f(x)在[1,e]上的最大值和最小值;
(2)求证:在区间[1,+∞)上,函数f(x)的图象在函数g(x)=x3-3x图象的下方.
解析 (1)由f(x)=x2-3x+2ln x,知f′(x)=x+-3==.
当x∈(1,2)时,f′(x)<0,∴f(x)在[1,2]上是减函数;
当x∈(2,e)时,f′(x)>0,∴f(x)在[2,e]上是增函数.
∴当x=2时,f(x)min=f(2)=2ln 2-4.
又f(1)=-,f(e)=e2-3e+2,
f(e)-f(1)=e2-3e+2-
=(e2-6e+9)=(e-3)2>0,
∴f(e)>f(1),∴f(x)max=f(e)=e2-3e+2.
综上,函数f(x)在[1,e]上的最大值为e2-3e+2,最小值为2ln 2-4.
(2)证明 设F(x)=x2-3x+2ln x-x3+3x,
则F′(x)=-3x2+x+==.
当x∈(1,+∞)时,F′(x)<0,∴F(x)在[1,+∞)上是减函数,
且F(1)=-<0,故当x∈[1,+∞)时,F(x)<0,
∴x2-3x+2ln x<x3-3x.
∴在区间[1,+∞)上,函数f(x)的图象在函数g(x)=x3-3x图象的下方.
12.设f(x)=ex-1.
(1)当x>-1时,证明:f(x)>;
(2)当a>ln 2-1且x>0时,证明:f(x)>x2-2ax.
证明 (1)当x>-1时,f(x)>,
即ex-1>=2x-1,
故结论成立当且仅当ex>2x,即ex-2x>0.
令g(x)=ex-2x,则g′(x)=ex-2.
令g′(x)=0,即ex-2=0,解得x=ln 2.
当x∈(-1,ln 2)时,g′(x)=ex-2<0,
故函数g(x)在(-1,ln 2]上单调递减;
当x∈(ln 2,+∞)时,g′(x)=ex-2>0,
故函数g(x)在[ln 2,+∞)上单调递增.
所以g(x)在(-1,+∞)上的最小值为g(ln 2)=eln 2-2ln 2=2(1-ln 2)>0,
所以在(-1,+∞)上有g(x)≥g(ln 2)>0,即ex>2x.
故当x∈(-1,+∞)时,有f(x)>.
(2)f(x)>x2-2ax,即ex-1>x2-2ax,也就是ex-x2+2ax-1>0.
令g(x)=ex-x2+2ax-1,则g′(x)=ex-2x+2a.
令h(x)=ex-2x+2a,则h′(x)=ex-2.
由(1),可知当x∈(-∞,ln 2)时,h′(x)<0,函数h(x)单调递减;
当x∈(ln 2,+∞)时,h′(x)>0,函数h(x)单调递增.
所以h(x)的最小值为h(ln 2)=eln 2-2ln 2+2a=2-2ln 2+2a.
因为a>ln 2-1,所以h(ln 2)>2-2ln 2+2(ln 2-1)=0,
即h(x)≥h(ln 2)>0.
所以g′(x)=h(x)>0,即g(x)在R上为增函数.
故g(x)在(0,+∞)上为增函数,所以g(x)>g(0).
而g(0)=0,所以g(x)=ex-x2+2ax-1>0,
即当a>ln 2-1且x>0时,f(x)>x2-2ax.
.精品资料。欢迎使用。 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
同课章节目录
