2021届高考数学二轮备考:立体几何-球与多面体的外接课件(共26张ppt)
文档属性
| 名称 | 2021届高考数学二轮备考:立体几何-球与多面体的外接课件(共26张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-30 21:28:42 | ||
图片预览








文档简介
2021高考数学备考:立体几何-球与多面体的外接课件(26张ppt)
2021年3月
一、考情分析
近几年高考对于组合体的考查,与球相关的外接与内切问题为高频考点,主要考查球与几何体的切接问题,在高考中主要的题型是选择题或者填空题,基本上都是中等难度的试题.要求学生有较强的空间想象能力和准确的计算能力,教学中要注重对学生直观想象,数学运算和数学建模等核心的培养.体会数形结合与转化思想在立体几何中的应用.
把握课堂里的每一分钟,体验成功与感动
-2-
要点导航
一.近五年高考题研究
二.常见几何体与外接球常见的类型
三.课堂小结
-3-
一、高考题研究
-4-
1.(5 分)已知A,B是球0的球面上两点,∠AOB=90O,
C为该球面上的动点,若三棱锥O- ABC体积的最大值为36,则球O的表面积为( )
A.36π B. 64π C. 144π D. 256π
2. (5分)体积为8的正方体的顶点都在同一球面上,则该球面的表面积为( )
A.12π B. π C.8π D.4π
-5-
3. (5分)在封闭的直三棱柱ABC-A1B1C1内有一个体积为V的球,若AB⊥BC,AB=6,BC=8,AA1=3,则V的最大值是( )
A.4兀 B.4.5兀 C.6兀 D. 兀
4. (5分)已知三棱锥S-ABC的所有顶点都在球O的球面上,SC是球O的直径.若平面SCA⊥平面SCB, SA=AC,SB=BC,三棱锥S-ABC的体积为9,则球O的表面积为 .
-6-
5 .(5分) 长方体的长、宽、高分别为3, 2,1, 其顶点都在球O的球面上,则球O的表面积为 14π .
6. (5分)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为( )
A.兀 B.0.75兀 C.0.5兀 D.0.25兀
-7-
研 究 结 论
1.年年考,难度有增加的趋势;
2.多为规则几何体;
3.由特殊几何体转为先探究几何体的特征再求解。
-8-
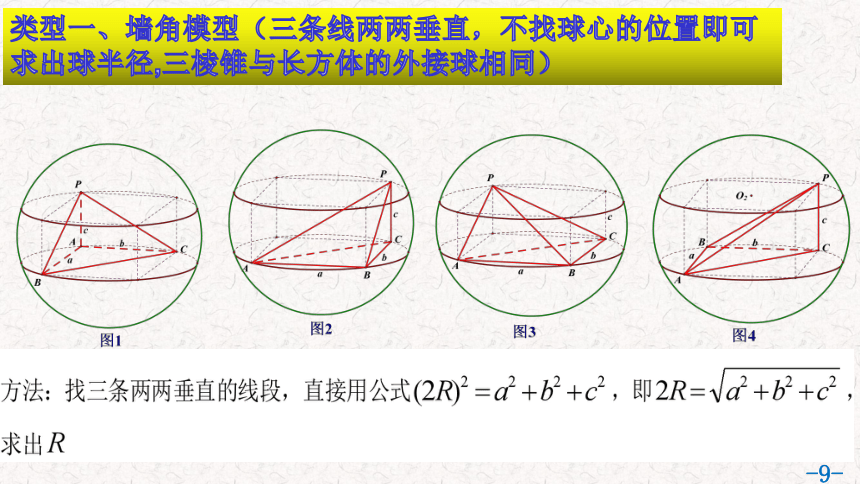
类型一、墙角模型(三条线两两垂直,不找球心的位置即可求出球半径,三棱锥与长方体的外接球相同)
-9-
解法一:
-10-
-11-
解法二:空间向量
PA,PB,PC两两垂直
-12-
类型一、总结
特点:线面垂直且底面是直角三角形(从长方体上底面取一个点,下底面取三个点的三棱锥)
-13-
类型二、对棱相等模型(补形为长方体)
-14-
练习1
-15-
-16-
类型三、垂面模型(一条直线垂直于一个平面)
-17-
-18-
-19-
例题
类型三、总结
球的球心一定在过小圆的圆心且与圆面垂直的直线上
-20-
类型四、切瓜模型(两个平面互相垂直)
-21-
-22-
解
通过两截面圆圆心且垂直于两平面的两直线的交点
拓展
-23-
类型四、总结
确定球心的一种通用方法——球的“垂径定理”(类比于圆的垂径定理而命名)
(1)球的“垂径定理”:球心与任一截面圆心的连线垂直于截面;反之,任一截面通过圆心的垂线穿过球心。
(2)确定球心的一种通用方法:根据以上性质,首先找几何体的一个内接面的外接圆的圆心,通过圆心且垂直于该平面的直线一定穿过球心,同理,可找到一条垂直于另一内接面的外接圆的圆心的直线;则两直线交点即为球心。
-24-
1.求解外接球问题的关键:确定球心
2.确定球心的方法:
(1)割补法(实用技巧)。某些特殊几何体的外接球时,可考虑将其补全为正方体或长方体,这样球的中心就与正方体或长方体中心重合了(这是本质所在)。
(2)确定球心的一种通用方法——球的“垂径定理”(类比于圆的垂径定理而命名)
球的“垂径定理”:球心与任一截面圆心的连线垂直于截面;反之,任一截面通过圆心的垂线穿过球心。
(3)确定球心的一种通用方法:通过圆心且垂直于该平面的直线一定穿过球心,同理,可找到一条垂直于另一内接面的外接圆的圆心的直线;则两直线交点即为球心。
本讲总结
-25-
努力,就一定能成功!
谢谢
-26-
2021年3月
一、考情分析
近几年高考对于组合体的考查,与球相关的外接与内切问题为高频考点,主要考查球与几何体的切接问题,在高考中主要的题型是选择题或者填空题,基本上都是中等难度的试题.要求学生有较强的空间想象能力和准确的计算能力,教学中要注重对学生直观想象,数学运算和数学建模等核心的培养.体会数形结合与转化思想在立体几何中的应用.
把握课堂里的每一分钟,体验成功与感动
-2-
要点导航
一.近五年高考题研究
二.常见几何体与外接球常见的类型
三.课堂小结
-3-
一、高考题研究
-4-
1.(5 分)已知A,B是球0的球面上两点,∠AOB=90O,
C为该球面上的动点,若三棱锥O- ABC体积的最大值为36,则球O的表面积为( )
A.36π B. 64π C. 144π D. 256π
2. (5分)体积为8的正方体的顶点都在同一球面上,则该球面的表面积为( )
A.12π B. π C.8π D.4π
-5-
3. (5分)在封闭的直三棱柱ABC-A1B1C1内有一个体积为V的球,若AB⊥BC,AB=6,BC=8,AA1=3,则V的最大值是( )
A.4兀 B.4.5兀 C.6兀 D. 兀
4. (5分)已知三棱锥S-ABC的所有顶点都在球O的球面上,SC是球O的直径.若平面SCA⊥平面SCB, SA=AC,SB=BC,三棱锥S-ABC的体积为9,则球O的表面积为 .
-6-
5 .(5分) 长方体的长、宽、高分别为3, 2,1, 其顶点都在球O的球面上,则球O的表面积为 14π .
6. (5分)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为( )
A.兀 B.0.75兀 C.0.5兀 D.0.25兀
-7-
研 究 结 论
1.年年考,难度有增加的趋势;
2.多为规则几何体;
3.由特殊几何体转为先探究几何体的特征再求解。
-8-
类型一、墙角模型(三条线两两垂直,不找球心的位置即可求出球半径,三棱锥与长方体的外接球相同)
-9-
解法一:
-10-
-11-
解法二:空间向量
PA,PB,PC两两垂直
-12-
类型一、总结
特点:线面垂直且底面是直角三角形(从长方体上底面取一个点,下底面取三个点的三棱锥)
-13-
类型二、对棱相等模型(补形为长方体)
-14-
练习1
-15-
-16-
类型三、垂面模型(一条直线垂直于一个平面)
-17-
-18-
-19-
例题
类型三、总结
球的球心一定在过小圆的圆心且与圆面垂直的直线上
-20-
类型四、切瓜模型(两个平面互相垂直)
-21-
-22-
解
通过两截面圆圆心且垂直于两平面的两直线的交点
拓展
-23-
类型四、总结
确定球心的一种通用方法——球的“垂径定理”(类比于圆的垂径定理而命名)
(1)球的“垂径定理”:球心与任一截面圆心的连线垂直于截面;反之,任一截面通过圆心的垂线穿过球心。
(2)确定球心的一种通用方法:根据以上性质,首先找几何体的一个内接面的外接圆的圆心,通过圆心且垂直于该平面的直线一定穿过球心,同理,可找到一条垂直于另一内接面的外接圆的圆心的直线;则两直线交点即为球心。
-24-
1.求解外接球问题的关键:确定球心
2.确定球心的方法:
(1)割补法(实用技巧)。某些特殊几何体的外接球时,可考虑将其补全为正方体或长方体,这样球的中心就与正方体或长方体中心重合了(这是本质所在)。
(2)确定球心的一种通用方法——球的“垂径定理”(类比于圆的垂径定理而命名)
球的“垂径定理”:球心与任一截面圆心的连线垂直于截面;反之,任一截面通过圆心的垂线穿过球心。
(3)确定球心的一种通用方法:通过圆心且垂直于该平面的直线一定穿过球心,同理,可找到一条垂直于另一内接面的外接圆的圆心的直线;则两直线交点即为球心。
本讲总结
-25-
努力,就一定能成功!
谢谢
-26-
同课章节目录
