六年级下册数学课件 6.5.4 有趣的平衡 人教版 24张
文档属性
| 名称 | 六年级下册数学课件 6.5.4 有趣的平衡 人教版 24张 |  | |
| 格式 | pptx | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-05 10:58:02 | ||
图片预览



文档简介
有趣的平衡
整理和复习
6
80千克
70千克
你玩过跷跷板吗?
那平衡与什么有关呢?
活动1
选一根粗细均匀的竹竿(长约1m),在中点的位置打个小孔并拴上绳子。然后从中点开始每隔8cm做一个记号(可以刻一个小槽)。
1
2
3
4
0
1
2
3
4
孔打在竹竿的正中间,绳子长度合适,提起绳子后竹竿要保持平衡。
刻记号时尽量等距。
温馨提示
竹竿尽量粗细均匀。
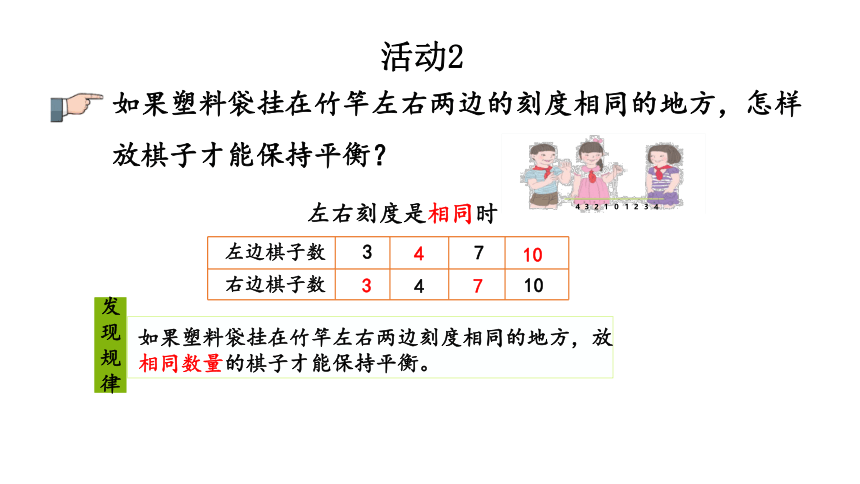
活动2
如果塑料袋挂在竹竿左右两边的刻度相同的地方,怎样放棋子才能保持平衡?
{5DA37D80-6434-44D0-A028-1B22A696006F} 左边棋子数
3
右边棋子数
3
4
4
7
7
10
10
左右刻度是相同时
发现规律
如果塑料袋挂在竹竿左右两边刻度相同的地方,放相同数量的棋子才能保持平衡。
1
2
3
4
0
1
2
3
4
活动3
如果左右塑料袋放入同样多的棋子,它们移动到什么位置才能保持平衡?
{5DA37D80-6434-44D0-A028-1B22A696006F} 左边刻度
5
右边刻度
5
1
2
4
4
1
2
左右放入同样多个棋子时
发现规律
如果左右塑料袋放入同样多的棋子,它们移动到距中点相同的位置才能保证平衡。
1
2
3
4
0
1
2
3
4
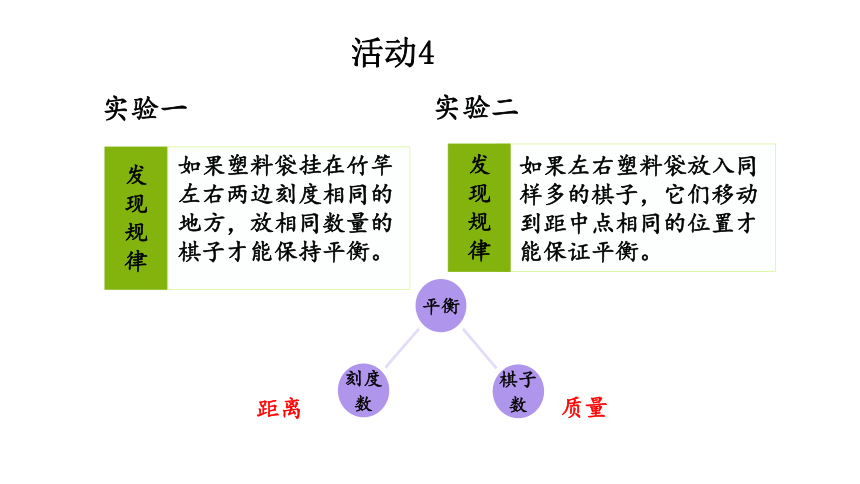
活动4
发现规律
如果塑料袋挂在竹竿左右两边刻度相同的地方,放相同数量的棋子才能保持平衡。
距离
实验一
实验二
如果左右塑料袋放入同样多的棋子,它们移动到距中点相同的位置才能保证平衡。
刻度数
平衡
棋子数
发现规律
质量
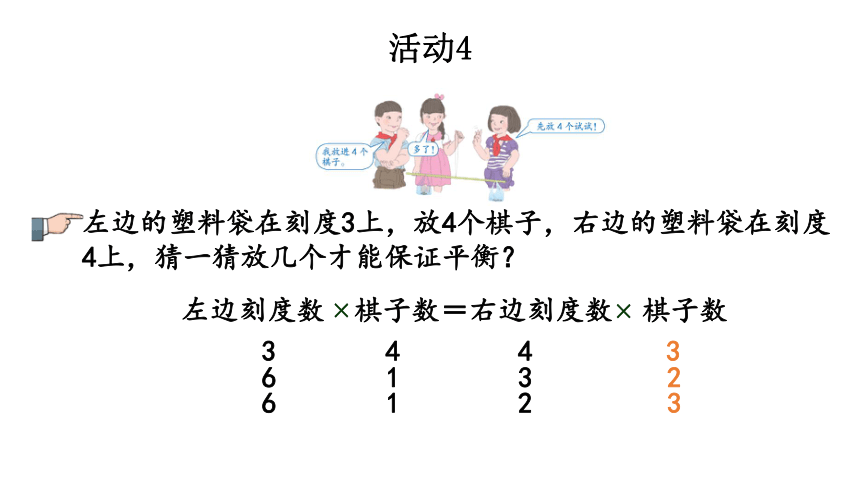
左边的塑料袋在刻度3上,放4个棋子,右边的塑料袋在刻度4上,猜一猜放几个才能保证平衡?
6
3
4
4
3
1
3
2
6
1
2
3
左边刻度数 棋子数=右边刻度数 棋子数
×
×
活动4
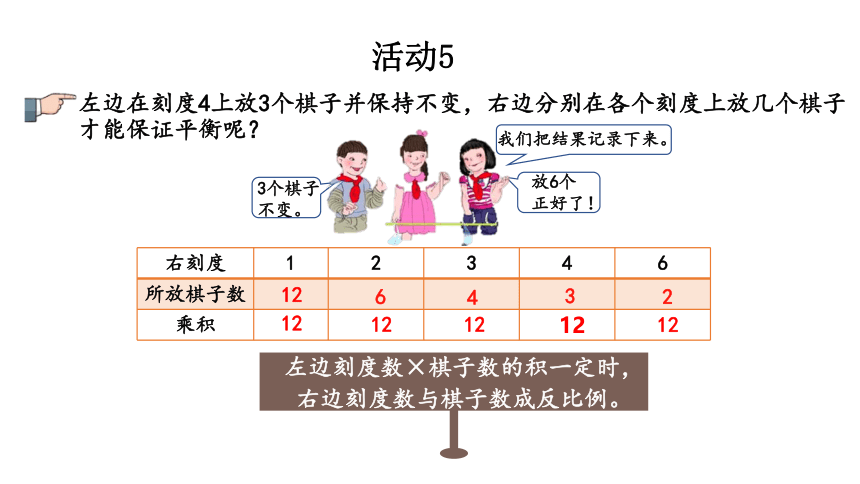
左边在刻度4上放3个棋子并保持不变,右边分别在各个刻度上放几个棋子
才能保证平衡呢?
12
12
6
12
12
12
4
3
2
{5DA37D80-6434-44D0-A028-1B22A696006F}右刻度
1
2
3
4
6
所放棋子数
乘积
左边刻度数×棋子数的积一定时,右边刻度数与棋子数成反比例。
3个棋子不变。
放6个正好了!
我们把结果记录下来。
12
活动5
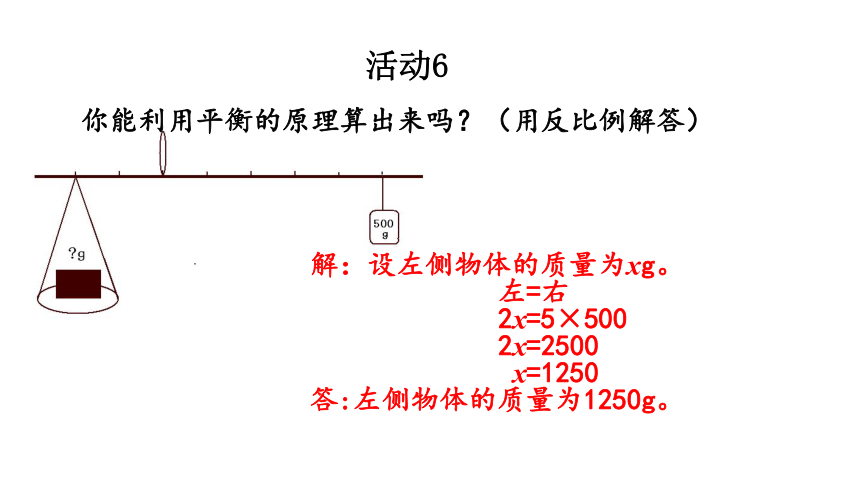
你能利用平衡的原理算出来吗?(用反比例解答)
解:设左侧物体的质量为xg。
左=右
2x=5×500
2x=2500
x=1250
答:左侧物体的质量为1250g。
活动6
小知识
同学们经常玩的跷跷板,有时候能够达到左右平衡,就是应用了杠杆原理。像右图那样,用一根硬的棍子,垫一块小石头,一个人能把一块大石头撬起来,这也是运用了杠杆原理。像这样的棍子,就是杠杆,你还能举出一些生活中应用杠杆原理的例子吗?
生活中的数学
给我一个支点,
我就能撬起整个地球。
——阿基米德
总结规律
制作实验用具
有趣的平衡
探索规律,理解“杠杆原理”
活动总结
1、有趣的平衡
一、制作实验用具。
选一根粗细均匀的竹竿(长约1 m),在中点的位置打个小孔并拴上绳子。然后从
中点开始每隔8 cm做一个记
号(可以刻一个小槽)。
二、探索规律,理解“杠杆原理”。
1.实验一。
如果塑料袋挂在竹竿左右两边刻度相同的地方,怎样放棋子才能保证平衡?
(1)实验尝试。
把两个塑料袋分别挂在竹竿左右两边刻度相同的地方。在左边的塑料袋里放上一定数量的棋子,发现竹竿不平衡,要保证竹竿平衡,
看右边要放几个棋子
(如下图)。
(2)实验记录如下表:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}左边棋子的个数/个
1
2
3
4
5
6
7
右边棋子的个数/个
1
2
3
4
5
6
7
(3)实验发现:从表中数据可以看出:左右两边所放的棋子数都相同。
(4)发现规律:如果塑料袋挂在竹竿左右两边刻度相同的地方,那么只要两个塑料袋里放相同数量的棋子,竹竿就能保证平衡。
2.实验二。
如果左右两个塑料袋放入同样多的棋子,它们移动到什么样的位置才能保证平衡?
(1)实验尝试:在两个塑料袋里分别放入数量相等的棋子,并挂在竹竿的两侧,来回移动塑料袋使竹竿保证平衡。
实验发现:放3个才能保证平衡。即:
左边的塑料袋在刻度3上放4个棋子
左边的塑料袋在刻度4上放3个棋子
两边平衡
发现规律:左边的刻度数×左边所放棋子数=3×4=12,右边的刻度数×右边所放棋子数=4×3=12,即:左边的刻度数×左边所放棋子数=右边的刻度数×右边所放棋子数。
(2)实验尝试2:如果左边的塑料袋在刻度6上放1个棋子,右边的塑料袋在刻度3上放几个呢?在刻度2上呢?
实验发现:在刻度3上放2个棋子,在刻度2上放3个棋子, 就能保证平衡。即:
左边的塑料袋在刻度3上放4个棋子
左边的塑料袋在刻度4上放3个棋子
两边平衡
发现规律:左边的刻度数×左边所放棋子数=6×1=6,右边的刻度数×右边所放棋子数=3×2=2×3=6。即:左边的刻度数×左边所放棋子数=右边的刻度数×右边所放棋子数。
4.总结规律。
要使竹竿平衡,必须满足“左边的刻度数×左边所放棋子数=右边的刻度数×右边所放棋子数”。
活动总结:
1.竹竿平衡的规律(即杠杆原理):当竹竿平衡时,左边的刻度数×左边所放棋子数=右边的刻度数×右边所放棋子数。
2.竹竿平衡,如果“左边的刻度数×左边所放棋子数”的积一定时,右边的刻度数与右边所放棋子数成反比例关系;反之也成立。
仔细想,认真填。
(1)左边刻度3处挂6个棋子,右边刻度2处应挂( )个棋子才能保持平衡。
(2)左边刻度1处挂4个棋子,现在要在右边挂1个棋子,应挂在刻度( )处才能保持平衡。
9
4
仔细想,认真填。
(3)要保持平衡,在一侧的刻度数和所挂棋子数乘积一定的情况下,另一侧的刻度数和所挂的棋子数成( )比例关系。
反
整理和复习
6
80千克
70千克
你玩过跷跷板吗?
那平衡与什么有关呢?
活动1
选一根粗细均匀的竹竿(长约1m),在中点的位置打个小孔并拴上绳子。然后从中点开始每隔8cm做一个记号(可以刻一个小槽)。
1
2
3
4
0
1
2
3
4
孔打在竹竿的正中间,绳子长度合适,提起绳子后竹竿要保持平衡。
刻记号时尽量等距。
温馨提示
竹竿尽量粗细均匀。
活动2
如果塑料袋挂在竹竿左右两边的刻度相同的地方,怎样放棋子才能保持平衡?
{5DA37D80-6434-44D0-A028-1B22A696006F} 左边棋子数
3
右边棋子数
3
4
4
7
7
10
10
左右刻度是相同时
发现规律
如果塑料袋挂在竹竿左右两边刻度相同的地方,放相同数量的棋子才能保持平衡。
1
2
3
4
0
1
2
3
4
活动3
如果左右塑料袋放入同样多的棋子,它们移动到什么位置才能保持平衡?
{5DA37D80-6434-44D0-A028-1B22A696006F} 左边刻度
5
右边刻度
5
1
2
4
4
1
2
左右放入同样多个棋子时
发现规律
如果左右塑料袋放入同样多的棋子,它们移动到距中点相同的位置才能保证平衡。
1
2
3
4
0
1
2
3
4
活动4
发现规律
如果塑料袋挂在竹竿左右两边刻度相同的地方,放相同数量的棋子才能保持平衡。
距离
实验一
实验二
如果左右塑料袋放入同样多的棋子,它们移动到距中点相同的位置才能保证平衡。
刻度数
平衡
棋子数
发现规律
质量
左边的塑料袋在刻度3上,放4个棋子,右边的塑料袋在刻度4上,猜一猜放几个才能保证平衡?
6
3
4
4
3
1
3
2
6
1
2
3
左边刻度数 棋子数=右边刻度数 棋子数
×
×
活动4
左边在刻度4上放3个棋子并保持不变,右边分别在各个刻度上放几个棋子
才能保证平衡呢?
12
12
6
12
12
12
4
3
2
{5DA37D80-6434-44D0-A028-1B22A696006F}右刻度
1
2
3
4
6
所放棋子数
乘积
左边刻度数×棋子数的积一定时,右边刻度数与棋子数成反比例。
3个棋子不变。
放6个正好了!
我们把结果记录下来。
12
活动5
你能利用平衡的原理算出来吗?(用反比例解答)
解:设左侧物体的质量为xg。
左=右
2x=5×500
2x=2500
x=1250
答:左侧物体的质量为1250g。
活动6
小知识
同学们经常玩的跷跷板,有时候能够达到左右平衡,就是应用了杠杆原理。像右图那样,用一根硬的棍子,垫一块小石头,一个人能把一块大石头撬起来,这也是运用了杠杆原理。像这样的棍子,就是杠杆,你还能举出一些生活中应用杠杆原理的例子吗?
生活中的数学
给我一个支点,
我就能撬起整个地球。
——阿基米德
总结规律
制作实验用具
有趣的平衡
探索规律,理解“杠杆原理”
活动总结
1、有趣的平衡
一、制作实验用具。
选一根粗细均匀的竹竿(长约1 m),在中点的位置打个小孔并拴上绳子。然后从
中点开始每隔8 cm做一个记
号(可以刻一个小槽)。
二、探索规律,理解“杠杆原理”。
1.实验一。
如果塑料袋挂在竹竿左右两边刻度相同的地方,怎样放棋子才能保证平衡?
(1)实验尝试。
把两个塑料袋分别挂在竹竿左右两边刻度相同的地方。在左边的塑料袋里放上一定数量的棋子,发现竹竿不平衡,要保证竹竿平衡,
看右边要放几个棋子
(如下图)。
(2)实验记录如下表:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}左边棋子的个数/个
1
2
3
4
5
6
7
右边棋子的个数/个
1
2
3
4
5
6
7
(3)实验发现:从表中数据可以看出:左右两边所放的棋子数都相同。
(4)发现规律:如果塑料袋挂在竹竿左右两边刻度相同的地方,那么只要两个塑料袋里放相同数量的棋子,竹竿就能保证平衡。
2.实验二。
如果左右两个塑料袋放入同样多的棋子,它们移动到什么样的位置才能保证平衡?
(1)实验尝试:在两个塑料袋里分别放入数量相等的棋子,并挂在竹竿的两侧,来回移动塑料袋使竹竿保证平衡。
实验发现:放3个才能保证平衡。即:
左边的塑料袋在刻度3上放4个棋子
左边的塑料袋在刻度4上放3个棋子
两边平衡
发现规律:左边的刻度数×左边所放棋子数=3×4=12,右边的刻度数×右边所放棋子数=4×3=12,即:左边的刻度数×左边所放棋子数=右边的刻度数×右边所放棋子数。
(2)实验尝试2:如果左边的塑料袋在刻度6上放1个棋子,右边的塑料袋在刻度3上放几个呢?在刻度2上呢?
实验发现:在刻度3上放2个棋子,在刻度2上放3个棋子, 就能保证平衡。即:
左边的塑料袋在刻度3上放4个棋子
左边的塑料袋在刻度4上放3个棋子
两边平衡
发现规律:左边的刻度数×左边所放棋子数=6×1=6,右边的刻度数×右边所放棋子数=3×2=2×3=6。即:左边的刻度数×左边所放棋子数=右边的刻度数×右边所放棋子数。
4.总结规律。
要使竹竿平衡,必须满足“左边的刻度数×左边所放棋子数=右边的刻度数×右边所放棋子数”。
活动总结:
1.竹竿平衡的规律(即杠杆原理):当竹竿平衡时,左边的刻度数×左边所放棋子数=右边的刻度数×右边所放棋子数。
2.竹竿平衡,如果“左边的刻度数×左边所放棋子数”的积一定时,右边的刻度数与右边所放棋子数成反比例关系;反之也成立。
仔细想,认真填。
(1)左边刻度3处挂6个棋子,右边刻度2处应挂( )个棋子才能保持平衡。
(2)左边刻度1处挂4个棋子,现在要在右边挂1个棋子,应挂在刻度( )处才能保持平衡。
9
4
仔细想,认真填。
(3)要保持平衡,在一侧的刻度数和所挂棋子数乘积一定的情况下,另一侧的刻度数和所挂的棋子数成( )比例关系。
反
