2020年新高考全国卷Ⅱ数学高考试题(海南)(word版含答案)
文档属性
| 名称 | 2020年新高考全国卷Ⅱ数学高考试题(海南)(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 884.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-19 16:28:53 | ||
图片预览



文档简介
2020 年普通高等学校招生全国统一考试
数学(海南)
注意事项:
1.答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写在本试 卷上无效.
3.考试结束后,将本试卷和答题卡一并交回.
一、选择题(本题共 8 小题,每小题 5 分,共 40 分.在每小题给出的四个选项中,只有一项符合题目要求的)
1、设集合A{2,3,5,7},B={1,2,3,5,8},则=( )
A. {1,3,5,7} B. {2,3} C. { 2,3,5} D.{1,2,3,5,7,8}
2、 =( )
A. B. C. D.
在中,D是AB边上的中点,则=( )
A. B. C. D.
4、日晷是中国古代用来测定时间的仪器,利用与晷面垂直的
晷针投射到晷面的影子来测定时间.把地球看成一个球(球心
记为O),地球上一点 A的纬度是指OA与地球赤道所在平面
所成角,点 A 处的水平面是指过点 A 且与OA垂直的平面.
在点 A处放置一个日晷,若晷面与赤道所在平面平行,点
A处的纬度为北纬,则晷针与点 A处的水平面所成角为( )
A. B. C. D.
5、某中学的学生积极参加体育锻炼,其中有 96%的学生喜欢足球或游泳,60%的学生喜欢足球,82%的学生喜欢游泳,则该中学既喜欢足球又喜欢游泳的学生数占该校学生总数的比例是 ( )
A.62 B.56 C.46 D.42
6、要安排3名学生到2个乡村做志愿者,每名学生只能选择去一个村,每个村里至少有一名志愿者,则不同的安排方法共有( )
A.2种 B.3种 C.6种 D.8种
7、已知函数在上单调递增,则的取值范围是( )
A. B. C. D.
8、若定义在 R 上的奇函数在单调递减,且,则满足 的的取值范围是( )
A. B. C. D.
二、选择题(本题共 4 小题,每小题 5 分,共 20 分.在每小题给出的选项中,有多项符合题目要求.全部选对的得 5 分,有选错的得 0 分,部分选对的得 3 分)
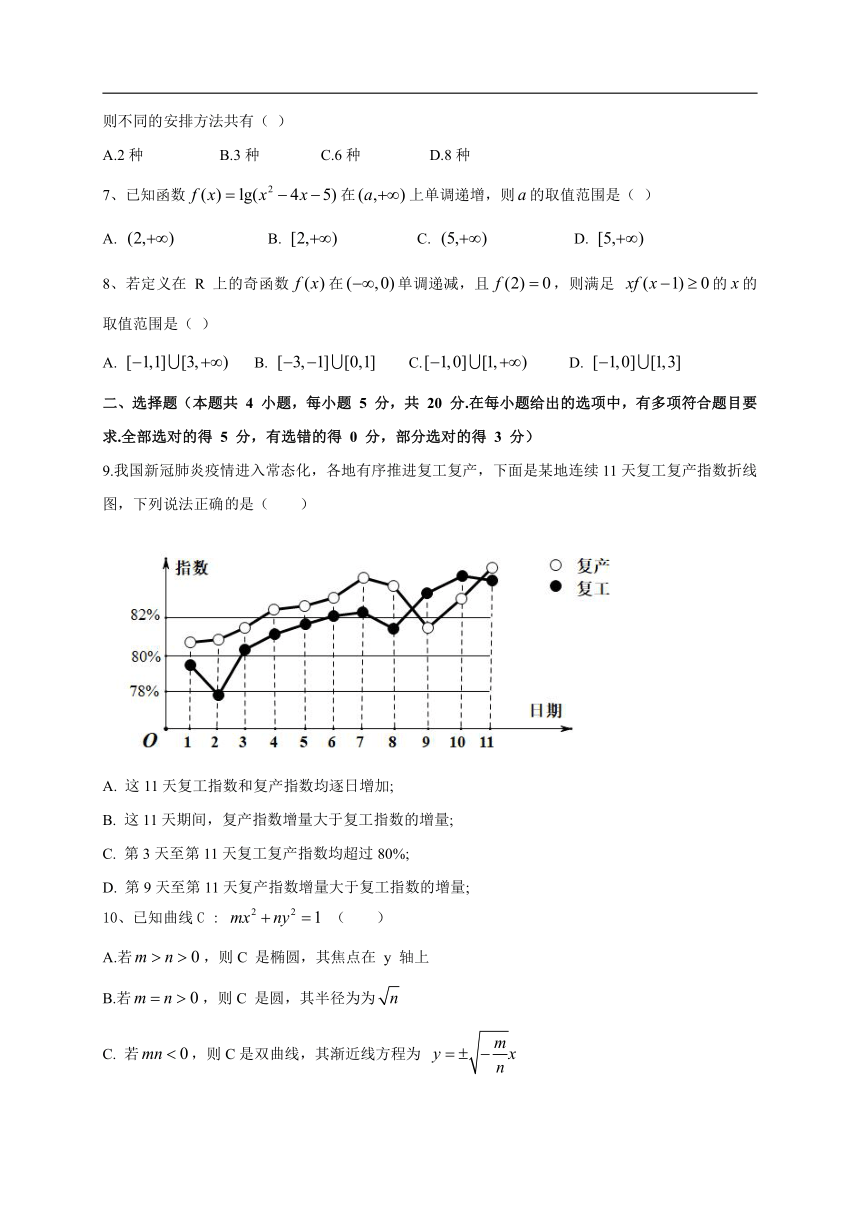
9.我国新冠肺炎疫情进入常态化,各地有序推进复工复产,下面是某地连续11天复工复产指数折线图,下列说法正确是( )
A. 这11天复工指数和复产指数均逐日增加;
B. 这11天期间,复产指数增量大于复工指数的增量;
C. 第3天至第11天复工复产指数均超过80%;
D. 第9天至第11天复产指数增量大于复工指数的增量;
10、已知曲线C : ( )
A.若,则C 是椭圆,其焦点在 y 轴上
B.若,则C 是圆,其半径为为
C. 若,则C是双曲线,其渐近线方程为
D.若,则C 是两条直线
11、右图是函数,则( )
A. B . C. D .
12、已知a 0, b 0,且a b1,则( )
A. B . C. D .
三、填空题(本题共 4 小题,每小题 5 分,共 20 分)
13、已知正方体ABCD-A1B1C1D1的棱长为2,M、N分别为BB1、AB的中点,则三棱锥A-NMD1的体积为
14、斜率为的直线过抛物线的焦点,且与C交于A,B两点,则
15、将数列{2n -1}与 3n- 2}的公共项从小到大排列得到数列,则的前 n 项和为
16、某中学开展劳动实习,学生加工制作零件,零件的截面如图所示,O为圆孔及轮廓圆弧 AB 所在圆的圆心,A是圆弧 AB 与直线 AG 的切点,B 是圆弧 AB 与直线 BC 的切点,四边形 DEFG为矩形, BC DG,垂足为C, tan ,到直线DE 和 EF 的距离均为7cm ,圆孔半径为1cm ,则图中阴影部分的面积为
四、解答题(本题共 6 小题,共 70 分.解答应写出文字说明、证明过程或演算步骤. )
17、(10 分)
在①ac=,② c sin A 3,③c 这三个条件中任选一个,补充在下面问题中,若问题中的三角形存在,求c 的;若问题中的三角形不存在,说明理由.
问 题 : 是 否 存 在 ABC , 它 的内角 A, B,C 的 对边分别 为 ,且, ?
注:如果选择多个条件分别解答,按第一个解答计分.
18、(12 分)
已知公比大于 1 的等比数列满足
(1)求的通项公式;
(2)求
19、(12 分)
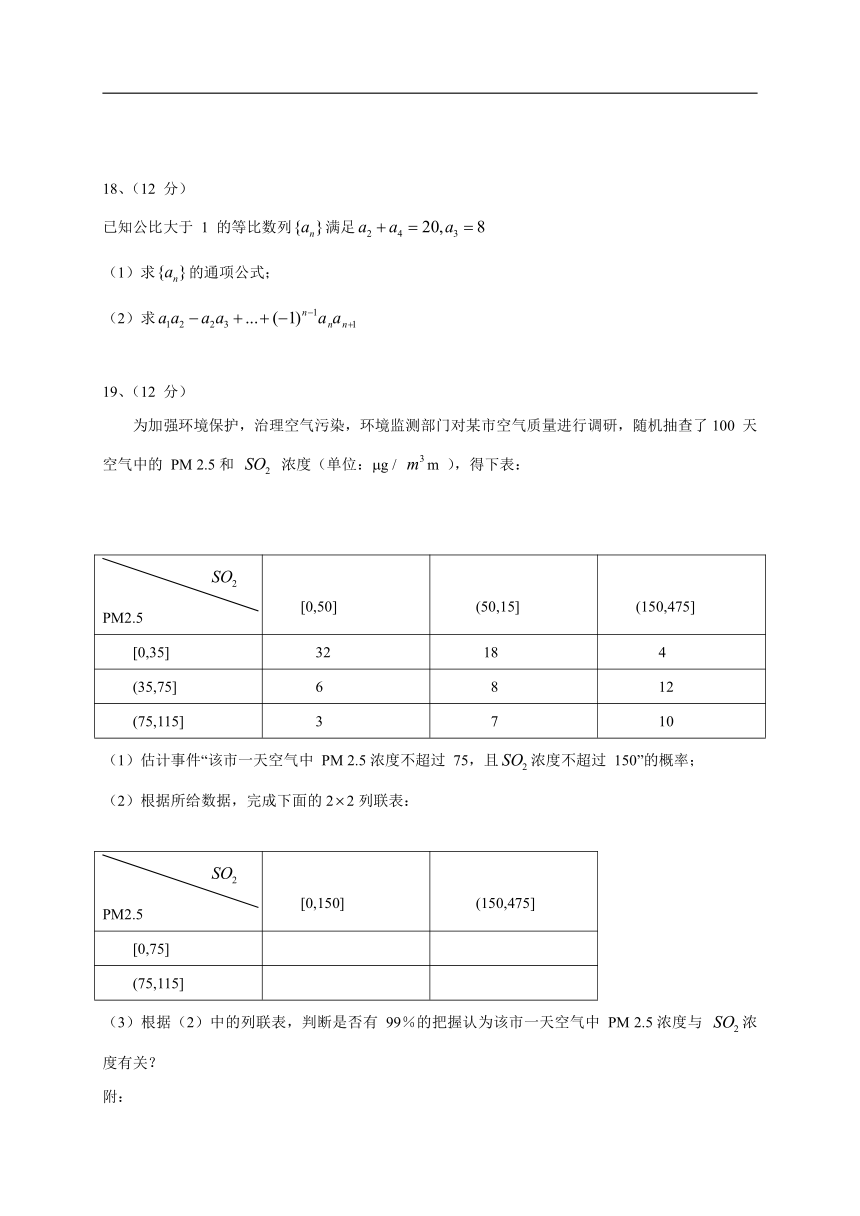
为加强环境保护,治理空气污染,环境监测部门对某市空气质量进行调研,随机抽查了100 天空气中的 PM 2.5和 浓度(单位:g / m ),得下表:
PM2.5
[0,50]
(50,15]
(150,475]
[0,35] 32 18 4
(35,75] 6 8 12
(75,115] 3 7 10
(1)估计事件“该市一天空气中 PM 2.5浓度不超过 75,且浓度不超过 150”的概率;
(2)根据所给数据,完成下面的22列联表:
PM2.5
[0,150]
(150,475]
[0,75]
(75,115]
(3)根据(2)中的列联表,判断是否有 99%的把握认为该市一天空气中 PM 2.5浓度与 浓度有关?
附:
20、(12分)如图,四棱锥 P ABCD的底面为正方形, PD 底面 ABCD .
设平面 PAD 与平面 PBC 的交线为 .
(1)证明:平面 PDC ;
(2)已知PD AD l ,Q为上的点,QB=,求 PB 与平面QCD 所成角的正弦值.
已知椭圆C:且过点 M(2,3),点A为其左顶点且AM的斜率为
(1)求C 的方程;
(2)点N 为椭圆上任意一点,求的面积的最大值.
22、已知函数
(1)当时,求曲线在点处的切线与两坐标轴围成的三角形的面积;
(2)若,求的取值范围.
2020 年普通高等学校招生全国统一考试
数学(海南)参考答案
一、选择题(本题共 8 小题,每小题 5 分,共 40 分.)
1. C 2.B 3. C 4. B 5. C 6.C 7. D 8. D
二、选择题(本题共 4 小题,每小题 5 分,共 20 分.在每小题给出的选项中,有多项符合题目要求.全部选对的得 5 分,有选错的得 0 分,部分选对的得 3 分)
9. CD 10. ACD 11. BC 12. ABD
三、填空题(本题共 4 小题,每小题 5 分,共 20 分)
13. 14. 15. 16.
四、解答题(本题共 6 小题,共 70 分.解答应写出文字说明、证明过程或演算步骤.)
17.
【分析】
解法一:由题意结合所给的条件,利用正弦定理角化边,得到a,b的比例关系,根据比例关系,设出长度长度,由余弦定理得到的长度,根据选择的条件进行分析判断和求解.
解法二:利用诱导公式和两角和的三角函数公式求得的值,得到角的值,然后根据选择的条件进行分析判断和求解.
【详解】解法一:
由可得:,
不妨设,
则:,即
选择条件①的解析:
据此可得:,,此时.
选择条件②的解析:
据此可得:,
则:,此时:,则:.
选择条件③的解析:
可得,,
与条件矛盾,则问题中的三角形不存在.
解法二:∵,
∴,
,
∴,∴,∴,∴,
若选①,,∵,∴,∴c=1;
若选②,,则,;
若选③,与条件矛盾.
18.
(1) 设等比数列的公比为q(q>1),则,
整理可得:,
,
数列的通项公式为:.
(2)由于:,故:
.
19.
(1)由表格可知,该市100天中,空气中的浓度不超过75,且浓度不超过150的天数有天,
所以该市一天中,空气中的浓度不超过75,且浓度不超过150的概率为;
(2)由所给数据,可得列联表为:
合计
64 16 80
10 10 20
合计 74 26 100
(3)根据列联表中的数据可得
,
因为根据临界值表可知,有的把握认为该市一天空气中浓度与浓度有关.
20.
(1)证明:
在正方形中,,
因为平面,平面,
所以平面,
又因为平面,平面平面,
所以,
因为在四棱锥中,底面是正方形,所以
且平面,所以
因为
所以平面;
(2)如图建立空间直角坐标系,
因为,则有,
设,则有,
因为QB=,所以有
设平面的法向量为,
则,即,
令,则,所以平面的一个法向量为,则
根据直线的方向向量与平面法向量所成角的余弦值的绝对值即为直线与平面所成角的正弦值,所以直线与平面所成角的正弦值等于
所以直线与平面所成角的正弦值为.
21.
(1)由题意可知直线AM的方程为:,即.
当y=0时,解得,所以a=4,
椭圆过点M(2,3),可得,
解得b2=12.
所以C的方程:.
(2)设与直线AM平行的直线方程为:,
如图所示,当直线与椭圆相切时,与AM距离比较远的直线与椭圆的切点为N,此时△AMN的面积取得最大值.
联立直线方程与椭圆方程,
可得:,
化简可得:,
所以,即m2=64,解得m=±8,
与AM距离比较远的直线方程:,
直线AM方程为:,
点N到直线AM的距离即两平行线之间的距离,
利用平行线之间的距离公式可得:,
由两点之间距离公式可得.
所以△AMN的面积的最大值:.
22.
(1),,.
,∴切点坐标为(1,1+e),
∴函数f(x)在点(1,f(1)处的切线方程为,即,
切线与坐标轴交点坐标分别为,
∴所求三角形面积为;
(2)解法一:,
,且.
设,则
∴g(x)在上单调递增,即在上单调递增,
当时,,∴,∴成立.
当时, ,,,
∴存在唯一,使得,且当时,当时,,,
因此
>1,
∴∴恒成立;
当时, ∴不是恒成立.
综上所述,实数a的取值范围是[1,+∞).
解法二:等价于
,
令,上述不等式等价于,
显然为单调增函数,∴又等价于,即,
令,则
在上h’(x)>0,h(x)单调递增;在(1,+∞)上h’(x)<0,h(x)单调递减,
∴,
,∴a的取值范围是[1,+∞).
数学(海南)
注意事项:
1.答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写在本试 卷上无效.
3.考试结束后,将本试卷和答题卡一并交回.
一、选择题(本题共 8 小题,每小题 5 分,共 40 分.在每小题给出的四个选项中,只有一项符合题目要求的)
1、设集合A{2,3,5,7},B={1,2,3,5,8},则=( )
A. {1,3,5,7} B. {2,3} C. { 2,3,5} D.{1,2,3,5,7,8}
2、 =( )
A. B. C. D.
在中,D是AB边上的中点,则=( )
A. B. C. D.
4、日晷是中国古代用来测定时间的仪器,利用与晷面垂直的
晷针投射到晷面的影子来测定时间.把地球看成一个球(球心
记为O),地球上一点 A的纬度是指OA与地球赤道所在平面
所成角,点 A 处的水平面是指过点 A 且与OA垂直的平面.
在点 A处放置一个日晷,若晷面与赤道所在平面平行,点
A处的纬度为北纬,则晷针与点 A处的水平面所成角为( )
A. B. C. D.
5、某中学的学生积极参加体育锻炼,其中有 96%的学生喜欢足球或游泳,60%的学生喜欢足球,82%的学生喜欢游泳,则该中学既喜欢足球又喜欢游泳的学生数占该校学生总数的比例是 ( )
A.62 B.56 C.46 D.42
6、要安排3名学生到2个乡村做志愿者,每名学生只能选择去一个村,每个村里至少有一名志愿者,则不同的安排方法共有( )
A.2种 B.3种 C.6种 D.8种
7、已知函数在上单调递增,则的取值范围是( )
A. B. C. D.
8、若定义在 R 上的奇函数在单调递减,且,则满足 的的取值范围是( )
A. B. C. D.
二、选择题(本题共 4 小题,每小题 5 分,共 20 分.在每小题给出的选项中,有多项符合题目要求.全部选对的得 5 分,有选错的得 0 分,部分选对的得 3 分)
9.我国新冠肺炎疫情进入常态化,各地有序推进复工复产,下面是某地连续11天复工复产指数折线图,下列说法正确是( )
A. 这11天复工指数和复产指数均逐日增加;
B. 这11天期间,复产指数增量大于复工指数的增量;
C. 第3天至第11天复工复产指数均超过80%;
D. 第9天至第11天复产指数增量大于复工指数的增量;
10、已知曲线C : ( )
A.若,则C 是椭圆,其焦点在 y 轴上
B.若,则C 是圆,其半径为为
C. 若,则C是双曲线,其渐近线方程为
D.若,则C 是两条直线
11、右图是函数,则( )
A. B . C. D .
12、已知a 0, b 0,且a b1,则( )
A. B . C. D .
三、填空题(本题共 4 小题,每小题 5 分,共 20 分)
13、已知正方体ABCD-A1B1C1D1的棱长为2,M、N分别为BB1、AB的中点,则三棱锥A-NMD1的体积为
14、斜率为的直线过抛物线的焦点,且与C交于A,B两点,则
15、将数列{2n -1}与 3n- 2}的公共项从小到大排列得到数列,则的前 n 项和为
16、某中学开展劳动实习,学生加工制作零件,零件的截面如图所示,O为圆孔及轮廓圆弧 AB 所在圆的圆心,A是圆弧 AB 与直线 AG 的切点,B 是圆弧 AB 与直线 BC 的切点,四边形 DEFG为矩形, BC DG,垂足为C, tan ,到直线DE 和 EF 的距离均为7cm ,圆孔半径为1cm ,则图中阴影部分的面积为
四、解答题(本题共 6 小题,共 70 分.解答应写出文字说明、证明过程或演算步骤. )
17、(10 分)
在①ac=,② c sin A 3,③c 这三个条件中任选一个,补充在下面问题中,若问题中的三角形存在,求c 的;若问题中的三角形不存在,说明理由.
问 题 : 是 否 存 在 ABC , 它 的内角 A, B,C 的 对边分别 为 ,且, ?
注:如果选择多个条件分别解答,按第一个解答计分.
18、(12 分)
已知公比大于 1 的等比数列满足
(1)求的通项公式;
(2)求
19、(12 分)
为加强环境保护,治理空气污染,环境监测部门对某市空气质量进行调研,随机抽查了100 天空气中的 PM 2.5和 浓度(单位:g / m ),得下表:
PM2.5
[0,50]
(50,15]
(150,475]
[0,35] 32 18 4
(35,75] 6 8 12
(75,115] 3 7 10
(1)估计事件“该市一天空气中 PM 2.5浓度不超过 75,且浓度不超过 150”的概率;
(2)根据所给数据,完成下面的22列联表:
PM2.5
[0,150]
(150,475]
[0,75]
(75,115]
(3)根据(2)中的列联表,判断是否有 99%的把握认为该市一天空气中 PM 2.5浓度与 浓度有关?
附:
20、(12分)如图,四棱锥 P ABCD的底面为正方形, PD 底面 ABCD .
设平面 PAD 与平面 PBC 的交线为 .
(1)证明:平面 PDC ;
(2)已知PD AD l ,Q为上的点,QB=,求 PB 与平面QCD 所成角的正弦值.
已知椭圆C:且过点 M(2,3),点A为其左顶点且AM的斜率为
(1)求C 的方程;
(2)点N 为椭圆上任意一点,求的面积的最大值.
22、已知函数
(1)当时,求曲线在点处的切线与两坐标轴围成的三角形的面积;
(2)若,求的取值范围.
2020 年普通高等学校招生全国统一考试
数学(海南)参考答案
一、选择题(本题共 8 小题,每小题 5 分,共 40 分.)
1. C 2.B 3. C 4. B 5. C 6.C 7. D 8. D
二、选择题(本题共 4 小题,每小题 5 分,共 20 分.在每小题给出的选项中,有多项符合题目要求.全部选对的得 5 分,有选错的得 0 分,部分选对的得 3 分)
9. CD 10. ACD 11. BC 12. ABD
三、填空题(本题共 4 小题,每小题 5 分,共 20 分)
13. 14. 15. 16.
四、解答题(本题共 6 小题,共 70 分.解答应写出文字说明、证明过程或演算步骤.)
17.
【分析】
解法一:由题意结合所给的条件,利用正弦定理角化边,得到a,b的比例关系,根据比例关系,设出长度长度,由余弦定理得到的长度,根据选择的条件进行分析判断和求解.
解法二:利用诱导公式和两角和的三角函数公式求得的值,得到角的值,然后根据选择的条件进行分析判断和求解.
【详解】解法一:
由可得:,
不妨设,
则:,即
选择条件①的解析:
据此可得:,,此时.
选择条件②的解析:
据此可得:,
则:,此时:,则:.
选择条件③的解析:
可得,,
与条件矛盾,则问题中的三角形不存在.
解法二:∵,
∴,
,
∴,∴,∴,∴,
若选①,,∵,∴,∴c=1;
若选②,,则,;
若选③,与条件矛盾.
18.
(1) 设等比数列的公比为q(q>1),则,
整理可得:,
,
数列的通项公式为:.
(2)由于:,故:
.
19.
(1)由表格可知,该市100天中,空气中的浓度不超过75,且浓度不超过150的天数有天,
所以该市一天中,空气中的浓度不超过75,且浓度不超过150的概率为;
(2)由所给数据,可得列联表为:
合计
64 16 80
10 10 20
合计 74 26 100
(3)根据列联表中的数据可得
,
因为根据临界值表可知,有的把握认为该市一天空气中浓度与浓度有关.
20.
(1)证明:
在正方形中,,
因为平面,平面,
所以平面,
又因为平面,平面平面,
所以,
因为在四棱锥中,底面是正方形,所以
且平面,所以
因为
所以平面;
(2)如图建立空间直角坐标系,
因为,则有,
设,则有,
因为QB=,所以有
设平面的法向量为,
则,即,
令,则,所以平面的一个法向量为,则
根据直线的方向向量与平面法向量所成角的余弦值的绝对值即为直线与平面所成角的正弦值,所以直线与平面所成角的正弦值等于
所以直线与平面所成角的正弦值为.
21.
(1)由题意可知直线AM的方程为:,即.
当y=0时,解得,所以a=4,
椭圆过点M(2,3),可得,
解得b2=12.
所以C的方程:.
(2)设与直线AM平行的直线方程为:,
如图所示,当直线与椭圆相切时,与AM距离比较远的直线与椭圆的切点为N,此时△AMN的面积取得最大值.
联立直线方程与椭圆方程,
可得:,
化简可得:,
所以,即m2=64,解得m=±8,
与AM距离比较远的直线方程:,
直线AM方程为:,
点N到直线AM的距离即两平行线之间的距离,
利用平行线之间的距离公式可得:,
由两点之间距离公式可得.
所以△AMN的面积的最大值:.
22.
(1),,.
,∴切点坐标为(1,1+e),
∴函数f(x)在点(1,f(1)处的切线方程为,即,
切线与坐标轴交点坐标分别为,
∴所求三角形面积为;
(2)解法一:,
,且.
设,则
∴g(x)在上单调递增,即在上单调递增,
当时,,∴,∴成立.
当时, ,,,
∴存在唯一,使得,且当时,当时,,,
因此
>1,
∴∴恒成立;
当时, ∴不是恒成立.
综上所述,实数a的取值范围是[1,+∞).
解法二:等价于
,
令,上述不等式等价于,
显然为单调增函数,∴又等价于,即,
令,则
在上h’(x)>0,h(x)单调递增;在(1,+∞)上h’(x)<0,h(x)单调递减,
∴,
,∴a的取值范围是[1,+∞).
同课章节目录
