江苏省南京市2012届高三数学二轮复习讲座4——立体几何二轮复习建议
文档属性
| 名称 | 江苏省南京市2012届高三数学二轮复习讲座4——立体几何二轮复习建议 | 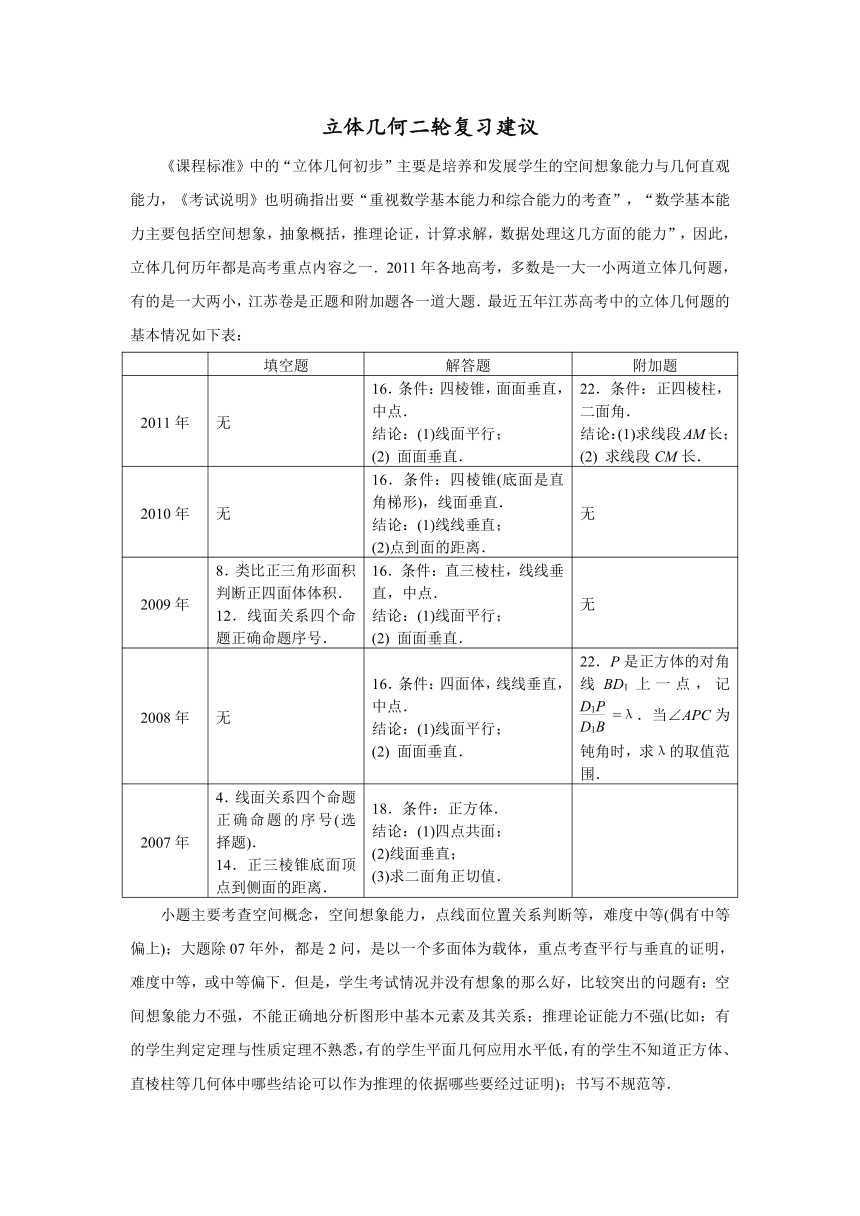 | |
| 格式 | zip | ||
| 文件大小 | 31.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-02 18:07:19 | ||
图片预览



文档简介
立体几何二轮复习建议
《课程标准》中的“立体几何初步”主要是培养和发展学生的空间想象能力与几何直观能力,《考试说明》也明确指出要“重视数学基本能力和综合能力的考查”,“数学基本能力主要包括空间想象,抽象概括,推理论证,计算求解,数据处理这几方面的能力”,因此,立体几何历年都是高考重点内容之一.2011年各地高考,多数是一大一小两道立体几何题,有的是一大两小,江苏卷是正题和附加题各一道大题.最近五年江苏高考中的立体几何题的基本情况如下表:
填空题 解答题 附加题
2011年 无 16.条件:四棱锥,面面垂直,中点.结论:(1)线面平行;(2) 面面垂直. 22.条件:正四棱柱,二面角.结论:(1)求线段AM长;(2) 求线段CM长.
2010年 无 16.条件:四棱锥(底面是直角梯形),线面垂直.结论:(1)线线垂直;(2)点到面的距离. 无
2009年 8.类比正三角形面积判断正四面体体积.12.线面关系四个命题正确命题序号. 16.条件:直三棱柱,线线垂直,中点.结论:(1)线面平行;(2) 面面垂直. 无
2008年 无 16.条件:四面体,线线垂直,中点.结论:(1)线面平行;(2) 面面垂直. 22.P是正方体的对角线BD1上一点,记=λ.当∠APC为钝角时,求λ的取值范围.
2007年 4.线面关系四个命题正确命题的序号(选择题).14.正三棱锥底面顶点到侧面的距离. 18.条件:正方体.结论:(1)四点共面;(2)线面垂直;(3)求二面角正切值.
小题主要考查空间概念,空间想象能力,点线面位置关系判断等,难度中等(偶有中等偏上);大题除07年外,都是2问,是以一个多面体为载体,重点考查平行与垂直的证明,难度中等,或中等偏下.但是,学生考试情况并没有想象的那么好,比较突出的问题有:空间想象能力不强,不能正确地分析图形中基本元素及其关系;推理论证能力不强(比如:有的学生判定定理与性质定理不熟悉,有的学生平面几何应用水平低,有的学生不知道正方体、直棱柱等几何体中哪些结论可以作为推理的依据哪些要经过证明);书写不规范等.
2012年,我们应该做好应对一个填空题一个解答题的准备,二轮复习中既要巩固基本题型和基本方法,又要提高空间想象能力和推理论证能力,有条件的要适当训练非标准图形的识别、平面图形的翻折等,适当改变解答题问的形式(落脚点还是平行与垂直),提高应变能力.在理科附加题中,要更加熟练地运用空间向量证明平行与垂直、计算空间的角,包括规范地建立空间直角坐标系,分清向量夹角与异面直线所成角、线面角、二面角.
基本题型一:空间几何体的认识及表面积与体积的计算(填空题)
例1.已知正四棱锥的底面边长是6,高为,这个正四棱锥的侧面积是 .
说明:本题主要考查正四棱锥的结构特征、空间几何体侧面积的计算方法,属容易题.
例2.已知矩形ABCD的顶点都在半径为4的球O的球面上,且AB=6,BC=,则棱锥O—ABCD的体积为 .
说明:本题主要考查球的几何特征以及相应的运算.球与其它几何体的组合问题,对空间想象能力要求较高,解决的关键是确定球心.
基本策略:涉及柱、锥、台、球及其简单组合体的侧面积和体积的计算问题,要在正确理解概念的基础上,画出符合题意的图形或辅助线(面),分析几何体的结构特征,选择合适的计算公式,另外要重视空间问题平面化的思想和割补法、等积转换法的运用.
基本题型二:空间中点线面位置关系的判断(填空题)
例3.设α和β为不重合的两个平面,给出下列命题:(1)若α内的两条相交直线分别平行于β内的两条直线,则α平行于β;(2)若α外一条直线l与α内的一条直线平行,则l和α平行;(3)设α和β相交于直线l,若α内有一条直线垂直于l,则α和β垂直;(4)直线l与α垂直的充分必要条件是l与α内的两条直线垂直.上面命题中,真命题的序号是 .(写出所有真命题的序号)
说明:这类题为高考常考题型,其实质为多项选择题.主要考查空间中线面之间的位置关系,要求熟悉有关公理、定理及推论,并具备较好的空间想象能力,做到不漏选、多选、错选,有一定难度.
例4.α、β为两个互相垂直的平面,a、b为一对异面直线,下列四个条件中是a⊥b的充分条件的有 .
a//α,bβ;②a⊥α,b//β;③a⊥α,b⊥β;
④a//α,b//β且a与α的距离等于b与β的距离.
说明:与例3一样,本题主要考查空间线面之间的位置关系,特别是判断平行与垂直的常用方法.
基本策略:正确转换符号语言、图形语言与文字语言;构造并利用具体模型(比如长方体),直观感知,操作确认;熟练运用4条公理、3条推论和10条定理来判断空间位置关系,通过证明或举反例来确定命题的真假.注意不要把平面几何结论简单类比到空间.
基本题型三:线线、线面、面面平行与垂直的证明(解答题)
例5.如图,在正三棱柱ABC—A1B1C1中,点D在边BC上,AD⊥C1D.
求证:AD⊥平面BB1C1C;
(2)如果E是边B1C1的中点,求证:A1E∥平面ADC1.
说明:这是《必修2》62页第17题,考查正三棱柱中的线面垂直和线面平行,实际上,还可以证明平面A1EB∥平面ADC1,平面ADC1⊥平面BB1C1C等.
09年江苏卷第16题:
如图,在直三棱柱ABC—A1B1C1中,E、F分别是A1B、A1C的中点,点D在B1C1上,A1D⊥B1C.
求证:(1)EF∥平面ABC;
(2)平面A1FD⊥平面BB1C1C.
例6.如图,四棱锥PABCD的底面是矩形,且AB=,E、F分别是棱AB、PC的中点.
求证:EF∥平面PAD;
(2)若点P在平面ABCD内的正投影O在直线AC上,求证:平面PAC⊥平面PDE.
说明:第(1)问方法较多,比较容易想到的有: ①取PD中点,构造平行四边形,证明线线平行;
②延长CE与DA相交,利用三角形中位性质证明线线平行;
③取CD中点,证明面面平行.
第(2)问中有关平面几何结论,一定要按照初中平面几何的要求,严格论证,不跳步.
例7.如图,四边形ABCD为矩形,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE.
(1)求证:AE⊥BE;
(2)求三棱锥D-AEC的体积;
(3)设M在线段AB上,且满足AM=2MB,试在线段CE上确定一点N,使得MN∥平面DAE.
说明:以多面体为载体,考查线线、线面、面面平行与垂直的判定与性质,是高考的常见题型.此类题既可以考查几何体的概念和性质,又能考查空间的线面关系,还有可以结合一些简单的运算,比较全面地考查学生的能力.本题中非常规放置的几何体及探究式的第3问,增加了难度.
基本策略:证明或探究空间中线线、线面、面面平行与垂直的位置关系,一要熟练掌握所有判定定理与性质定理,梳理好几种位置关系的常见证明方法,如证明线面平行,既可以构造线线平行,也可以构造面面平行.而证明线线平行常用的是三角形中位线性质,或构造平行四边形;二要用分析与综合相结合的方法来寻找证明的思路;三要注意表述规范,推理严谨,避免使用一些虽然正确但不能作为推理依据的结论.有条件时,可以适当涉及一些简单的计算,或是添加探究性的小问,或是在图形上作一点变化,但一定要控制难度,且最终的落脚点一定是平行与垂直.
11年三模第16题:
如图,在矩形ABCD中,AD=2,AB=4,E、F分别是边AB、AD的中点,现将△ADE沿DE折起,得四棱锥ABCDE.
求证:EF∥平面ABC;
若平面ADE⊥平面BCDE,求四面体FDCE的体积.
基本题型四:运用空间向量证明与计算(理科附加题)
例8.如图,在四棱锥PABCD中,底面ABCD是正方形,侧棱PD平面ABCD,且PD=DC,E是PC的中点,F是PB上一点,且EFPB.
(1) 求证:PA∥平面EDB;
(2) 求证:PB⊥平面EFD;
(3) 求二面角CPBD的余弦值大小.
说明:立体几何所讨论的问题主要有两类:一类是位置关系,判断线线、线面、面面平行或垂直关系;另一类是度量关系,求长度和角度.运用向量的方法是讨论这两类问题的通性通法.在本例中,可以利用几何体中的两两垂直的三条直线合理建立空间直角坐标系,用坐标表示有关向量,运用“算”的方法证明空间中的平行与垂直、计算二面角大小,也可以不建系,选三个不共线的向量组成基底,用来表示其它向量,再用“算”的方法证明平行与垂直、计算二面角大小.
例9.如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=,AF=1.
(1)求二面角A—DF—B的大小;
(2)在线段AC上找一点P,使PF与AD所成的角为600.
说明:本类题主要考查寻找三条两两垂直的三条直线合理建立空间直角坐标系,通过向量计算解决空间中的夹角问题(包括线线角、线面角与二面角)的能力,是高考的常见题型.
基本策略:空间向量的基础知识可以类比于《必修4》中平面向量的相关知识进行整理与记忆;通过建立适当的坐标系,用向量来表示点,刻画直线和平面的“方向”;理解用向量判定空间位置关系、求角的原理,并掌握一般解题步骤,其中,线线角、线面角与二面角是本类题型中的重点考查对象,应加强训练.此外,在计算平面的法向量、探究点的位置等问题中,要善于运用“待定系数法”合理设出坐标,寻找满足条件的方程(组)来解决问题.
二轮专题与课时建议:
专题 内容说明
第一课时 空间几何体及其表面积与体积 多面体与旋转体、直观图、表面积和体积以小题训练为主,有条件时,训练一点展开与折叠
第二课时 空间中点线面之间的位置关系 点、线、面之间的位置关系,线线、线面、面面平行与垂直的定义、判定和性质,平行与垂直的证明与探究以大题训练为主(强调书写规范),有条件时,采用板演和面批的方法,有针对地解决问题
第三课时 空间向量与立体几何 空间向量的概念及运算、应用(判定平行与垂直、计算空间的角)以大题训练为主,抓满分率
A
B
C
A1
B1
C1
E
F
D
B
E
A
F
D
C
《课程标准》中的“立体几何初步”主要是培养和发展学生的空间想象能力与几何直观能力,《考试说明》也明确指出要“重视数学基本能力和综合能力的考查”,“数学基本能力主要包括空间想象,抽象概括,推理论证,计算求解,数据处理这几方面的能力”,因此,立体几何历年都是高考重点内容之一.2011年各地高考,多数是一大一小两道立体几何题,有的是一大两小,江苏卷是正题和附加题各一道大题.最近五年江苏高考中的立体几何题的基本情况如下表:
填空题 解答题 附加题
2011年 无 16.条件:四棱锥,面面垂直,中点.结论:(1)线面平行;(2) 面面垂直. 22.条件:正四棱柱,二面角.结论:(1)求线段AM长;(2) 求线段CM长.
2010年 无 16.条件:四棱锥(底面是直角梯形),线面垂直.结论:(1)线线垂直;(2)点到面的距离. 无
2009年 8.类比正三角形面积判断正四面体体积.12.线面关系四个命题正确命题序号. 16.条件:直三棱柱,线线垂直,中点.结论:(1)线面平行;(2) 面面垂直. 无
2008年 无 16.条件:四面体,线线垂直,中点.结论:(1)线面平行;(2) 面面垂直. 22.P是正方体的对角线BD1上一点,记=λ.当∠APC为钝角时,求λ的取值范围.
2007年 4.线面关系四个命题正确命题的序号(选择题).14.正三棱锥底面顶点到侧面的距离. 18.条件:正方体.结论:(1)四点共面;(2)线面垂直;(3)求二面角正切值.
小题主要考查空间概念,空间想象能力,点线面位置关系判断等,难度中等(偶有中等偏上);大题除07年外,都是2问,是以一个多面体为载体,重点考查平行与垂直的证明,难度中等,或中等偏下.但是,学生考试情况并没有想象的那么好,比较突出的问题有:空间想象能力不强,不能正确地分析图形中基本元素及其关系;推理论证能力不强(比如:有的学生判定定理与性质定理不熟悉,有的学生平面几何应用水平低,有的学生不知道正方体、直棱柱等几何体中哪些结论可以作为推理的依据哪些要经过证明);书写不规范等.
2012年,我们应该做好应对一个填空题一个解答题的准备,二轮复习中既要巩固基本题型和基本方法,又要提高空间想象能力和推理论证能力,有条件的要适当训练非标准图形的识别、平面图形的翻折等,适当改变解答题问的形式(落脚点还是平行与垂直),提高应变能力.在理科附加题中,要更加熟练地运用空间向量证明平行与垂直、计算空间的角,包括规范地建立空间直角坐标系,分清向量夹角与异面直线所成角、线面角、二面角.
基本题型一:空间几何体的认识及表面积与体积的计算(填空题)
例1.已知正四棱锥的底面边长是6,高为,这个正四棱锥的侧面积是 .
说明:本题主要考查正四棱锥的结构特征、空间几何体侧面积的计算方法,属容易题.
例2.已知矩形ABCD的顶点都在半径为4的球O的球面上,且AB=6,BC=,则棱锥O—ABCD的体积为 .
说明:本题主要考查球的几何特征以及相应的运算.球与其它几何体的组合问题,对空间想象能力要求较高,解决的关键是确定球心.
基本策略:涉及柱、锥、台、球及其简单组合体的侧面积和体积的计算问题,要在正确理解概念的基础上,画出符合题意的图形或辅助线(面),分析几何体的结构特征,选择合适的计算公式,另外要重视空间问题平面化的思想和割补法、等积转换法的运用.
基本题型二:空间中点线面位置关系的判断(填空题)
例3.设α和β为不重合的两个平面,给出下列命题:(1)若α内的两条相交直线分别平行于β内的两条直线,则α平行于β;(2)若α外一条直线l与α内的一条直线平行,则l和α平行;(3)设α和β相交于直线l,若α内有一条直线垂直于l,则α和β垂直;(4)直线l与α垂直的充分必要条件是l与α内的两条直线垂直.上面命题中,真命题的序号是 .(写出所有真命题的序号)
说明:这类题为高考常考题型,其实质为多项选择题.主要考查空间中线面之间的位置关系,要求熟悉有关公理、定理及推论,并具备较好的空间想象能力,做到不漏选、多选、错选,有一定难度.
例4.α、β为两个互相垂直的平面,a、b为一对异面直线,下列四个条件中是a⊥b的充分条件的有 .
a//α,bβ;②a⊥α,b//β;③a⊥α,b⊥β;
④a//α,b//β且a与α的距离等于b与β的距离.
说明:与例3一样,本题主要考查空间线面之间的位置关系,特别是判断平行与垂直的常用方法.
基本策略:正确转换符号语言、图形语言与文字语言;构造并利用具体模型(比如长方体),直观感知,操作确认;熟练运用4条公理、3条推论和10条定理来判断空间位置关系,通过证明或举反例来确定命题的真假.注意不要把平面几何结论简单类比到空间.
基本题型三:线线、线面、面面平行与垂直的证明(解答题)
例5.如图,在正三棱柱ABC—A1B1C1中,点D在边BC上,AD⊥C1D.
求证:AD⊥平面BB1C1C;
(2)如果E是边B1C1的中点,求证:A1E∥平面ADC1.
说明:这是《必修2》62页第17题,考查正三棱柱中的线面垂直和线面平行,实际上,还可以证明平面A1EB∥平面ADC1,平面ADC1⊥平面BB1C1C等.
09年江苏卷第16题:
如图,在直三棱柱ABC—A1B1C1中,E、F分别是A1B、A1C的中点,点D在B1C1上,A1D⊥B1C.
求证:(1)EF∥平面ABC;
(2)平面A1FD⊥平面BB1C1C.
例6.如图,四棱锥PABCD的底面是矩形,且AB=,E、F分别是棱AB、PC的中点.
求证:EF∥平面PAD;
(2)若点P在平面ABCD内的正投影O在直线AC上,求证:平面PAC⊥平面PDE.
说明:第(1)问方法较多,比较容易想到的有: ①取PD中点,构造平行四边形,证明线线平行;
②延长CE与DA相交,利用三角形中位性质证明线线平行;
③取CD中点,证明面面平行.
第(2)问中有关平面几何结论,一定要按照初中平面几何的要求,严格论证,不跳步.
例7.如图,四边形ABCD为矩形,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE.
(1)求证:AE⊥BE;
(2)求三棱锥D-AEC的体积;
(3)设M在线段AB上,且满足AM=2MB,试在线段CE上确定一点N,使得MN∥平面DAE.
说明:以多面体为载体,考查线线、线面、面面平行与垂直的判定与性质,是高考的常见题型.此类题既可以考查几何体的概念和性质,又能考查空间的线面关系,还有可以结合一些简单的运算,比较全面地考查学生的能力.本题中非常规放置的几何体及探究式的第3问,增加了难度.
基本策略:证明或探究空间中线线、线面、面面平行与垂直的位置关系,一要熟练掌握所有判定定理与性质定理,梳理好几种位置关系的常见证明方法,如证明线面平行,既可以构造线线平行,也可以构造面面平行.而证明线线平行常用的是三角形中位线性质,或构造平行四边形;二要用分析与综合相结合的方法来寻找证明的思路;三要注意表述规范,推理严谨,避免使用一些虽然正确但不能作为推理依据的结论.有条件时,可以适当涉及一些简单的计算,或是添加探究性的小问,或是在图形上作一点变化,但一定要控制难度,且最终的落脚点一定是平行与垂直.
11年三模第16题:
如图,在矩形ABCD中,AD=2,AB=4,E、F分别是边AB、AD的中点,现将△ADE沿DE折起,得四棱锥ABCDE.
求证:EF∥平面ABC;
若平面ADE⊥平面BCDE,求四面体FDCE的体积.
基本题型四:运用空间向量证明与计算(理科附加题)
例8.如图,在四棱锥PABCD中,底面ABCD是正方形,侧棱PD平面ABCD,且PD=DC,E是PC的中点,F是PB上一点,且EFPB.
(1) 求证:PA∥平面EDB;
(2) 求证:PB⊥平面EFD;
(3) 求二面角CPBD的余弦值大小.
说明:立体几何所讨论的问题主要有两类:一类是位置关系,判断线线、线面、面面平行或垂直关系;另一类是度量关系,求长度和角度.运用向量的方法是讨论这两类问题的通性通法.在本例中,可以利用几何体中的两两垂直的三条直线合理建立空间直角坐标系,用坐标表示有关向量,运用“算”的方法证明空间中的平行与垂直、计算二面角大小,也可以不建系,选三个不共线的向量组成基底,用来表示其它向量,再用“算”的方法证明平行与垂直、计算二面角大小.
例9.如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=,AF=1.
(1)求二面角A—DF—B的大小;
(2)在线段AC上找一点P,使PF与AD所成的角为600.
说明:本类题主要考查寻找三条两两垂直的三条直线合理建立空间直角坐标系,通过向量计算解决空间中的夹角问题(包括线线角、线面角与二面角)的能力,是高考的常见题型.
基本策略:空间向量的基础知识可以类比于《必修4》中平面向量的相关知识进行整理与记忆;通过建立适当的坐标系,用向量来表示点,刻画直线和平面的“方向”;理解用向量判定空间位置关系、求角的原理,并掌握一般解题步骤,其中,线线角、线面角与二面角是本类题型中的重点考查对象,应加强训练.此外,在计算平面的法向量、探究点的位置等问题中,要善于运用“待定系数法”合理设出坐标,寻找满足条件的方程(组)来解决问题.
二轮专题与课时建议:
专题 内容说明
第一课时 空间几何体及其表面积与体积 多面体与旋转体、直观图、表面积和体积以小题训练为主,有条件时,训练一点展开与折叠
第二课时 空间中点线面之间的位置关系 点、线、面之间的位置关系,线线、线面、面面平行与垂直的定义、判定和性质,平行与垂直的证明与探究以大题训练为主(强调书写规范),有条件时,采用板演和面批的方法,有针对地解决问题
第三课时 空间向量与立体几何 空间向量的概念及运算、应用(判定平行与垂直、计算空间的角)以大题训练为主,抓满分率
A
B
C
A1
B1
C1
E
F
D
B
E
A
F
D
C
同课章节目录
