弧长及扇形的面积
图片预览





文档简介
(共30张PPT)
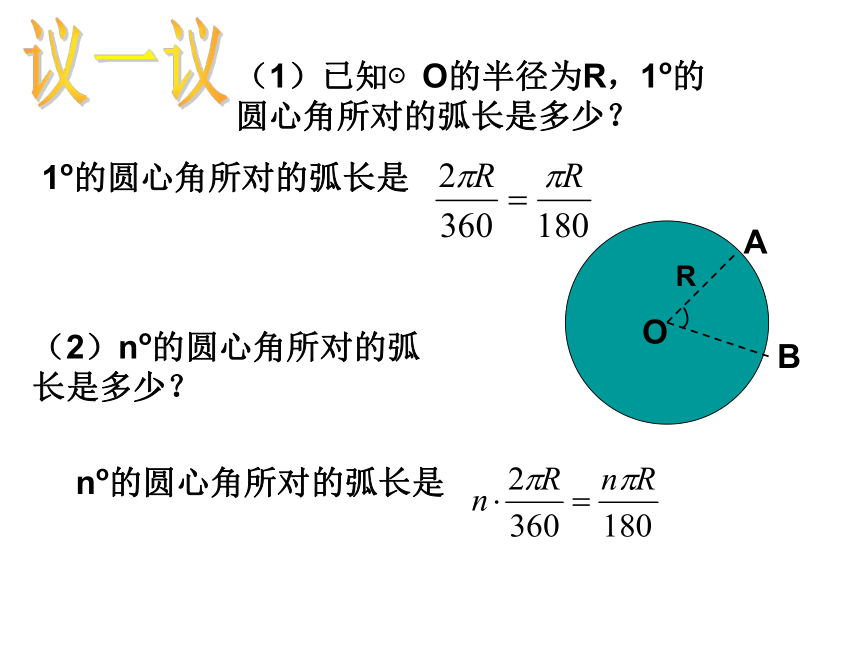
(1)已知⊙O的半径为R,1o的圆心角所对的弧长是多少?
A
B
O
R
(2)no的圆心角所对的弧长是多少?
1o的圆心角所对的弧长是
no的圆心角所对的弧长是
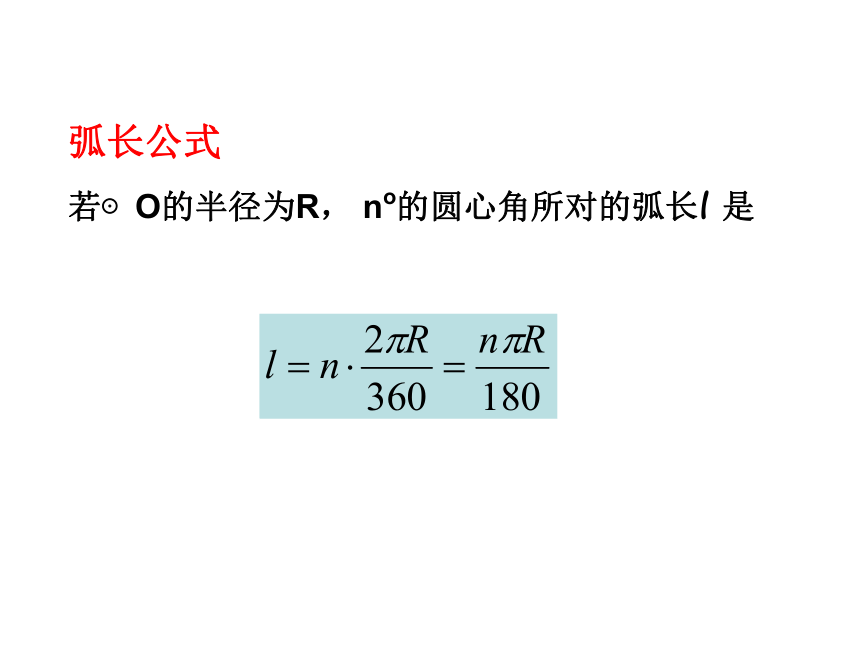
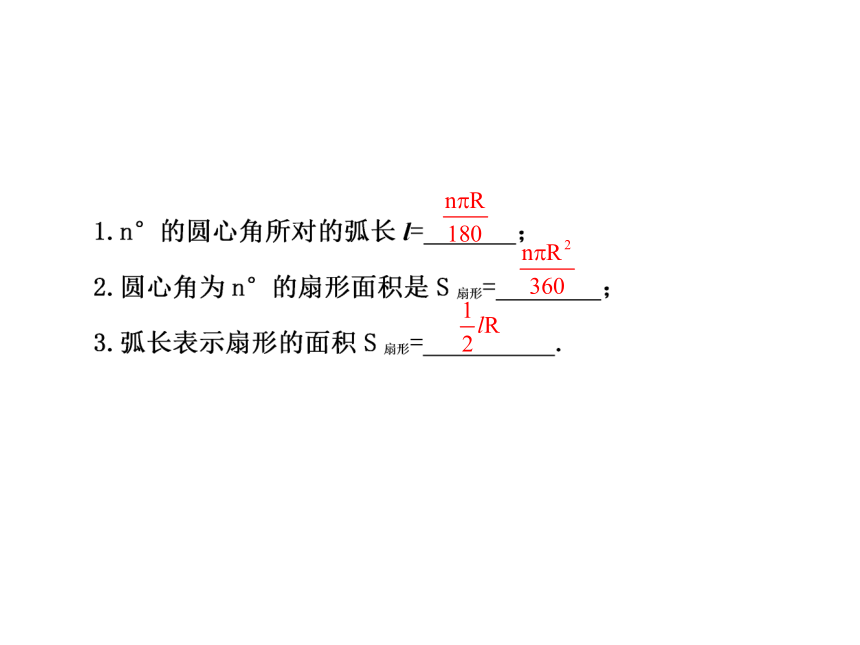
弧长公式
若⊙O的半径为R, no的圆心角所对的弧长l 是
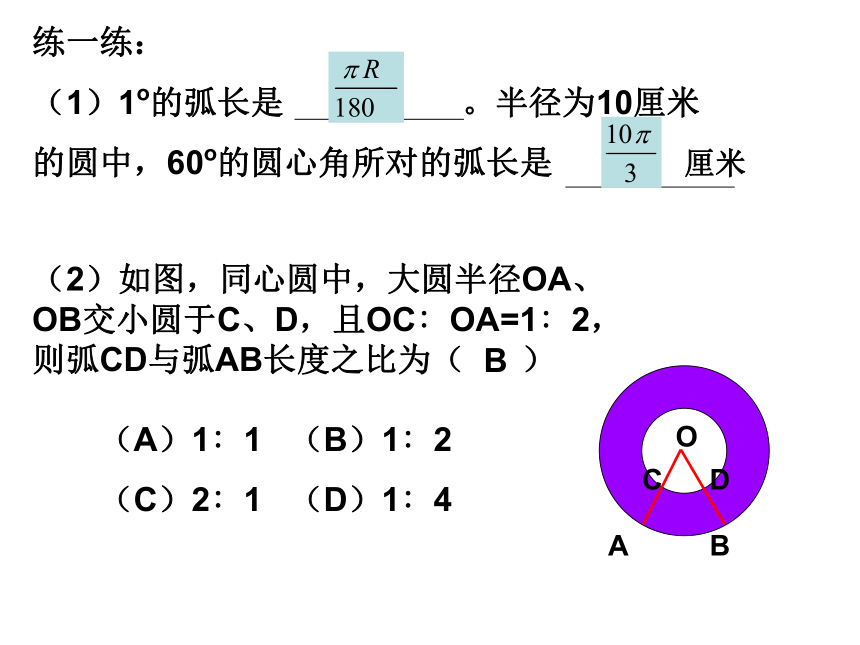
练一练:
(1)1o的弧长是 。半径为10厘米
的圆中,60o的圆心角所对的弧长是 厘米
(2)如图,同心圆中,大圆半径OA、OB交小圆于C、D,且OC∶OA=1∶2,则弧CD与弧AB长度之比为( )
O
A
B
C
D
(A)1∶1 (B)1∶2
(C)2∶1 (D)1∶4
B
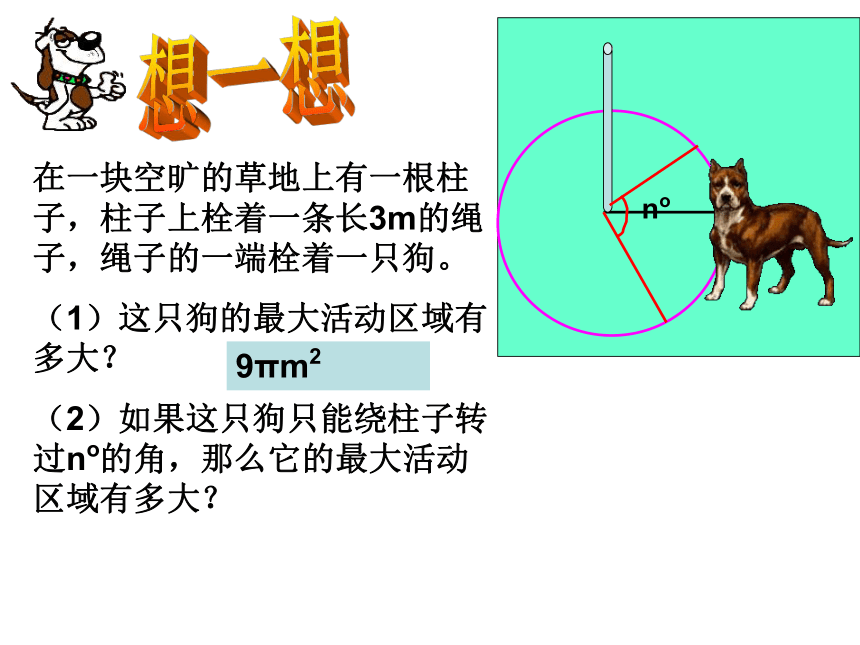
在一块空旷的草地上有一根柱子,柱子上栓着一条长3m的绳子,绳子的一端栓着一只狗。
(1)这只狗的最大活动区域有多大?
(2)如果这只狗只能绕柱子转过no的角,那么它的最大活动区域有多大?
9πm2
no
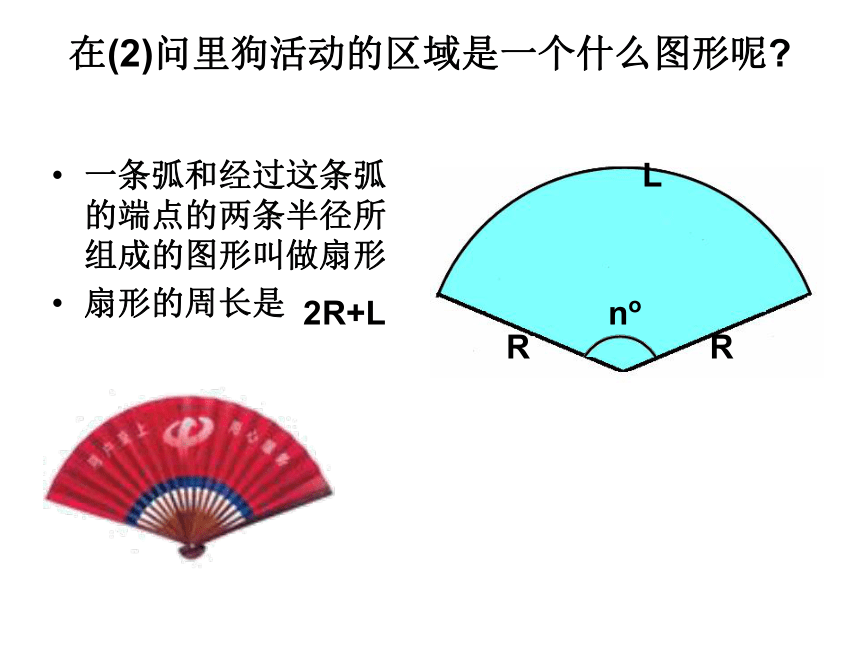
在(2)问里狗活动的区域是一个什么图形呢
一条弧和经过这条弧的端点的两条半径所组成的图形叫做扇形
扇形的周长是
2R+L
no
R
R
L
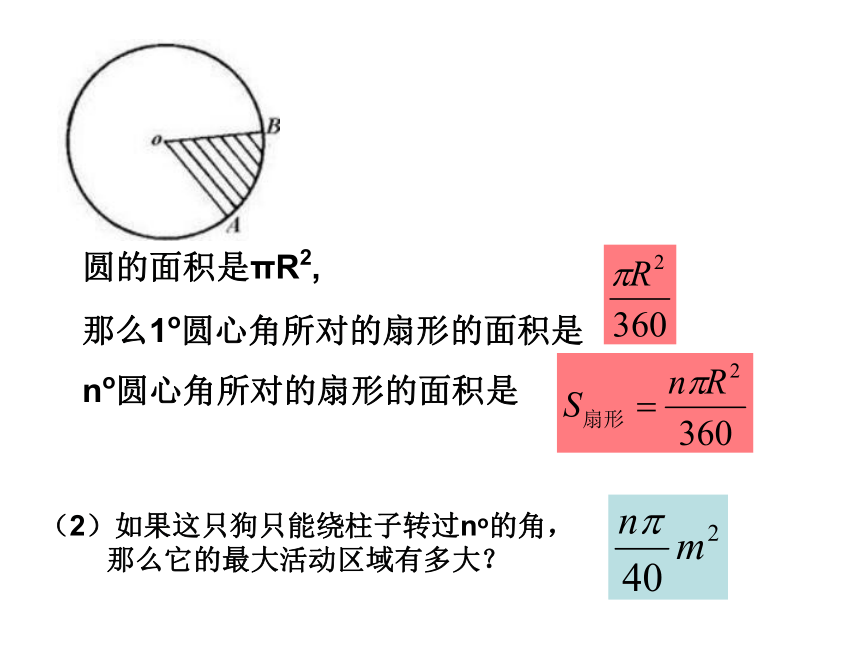
圆的面积是πR2,
那么1o圆心角所对的扇形的面积是
no圆心角所对的扇形的面积是
(2)如果这只狗只能绕柱子转过no的角,那么它的最大活动区域有多大?
弧长公式与扇形的面积公式之间的联系:
(1)当已知弧长L和半径R, 求扇形面积时,应选用
(2)当已知半径和圆心角的度数,求扇形面积时,应选用
例2:已知扇形AOB的半径为12cm,∠AOB=120o,求弧AB的长和扇形AOB的面积.
一个扇形的圆心角为90o,半径为2,
则弧长= ,扇形面积= .
2. 一个扇形的弧长为20πcm,面积是240πc㎡,则该扇形的圆心角为 .
已知扇形的圆心角为120o,半径为6,则扇形的弧长是 ( )
A. 3π B.4π C.5π D.6π
π
π
150o
B
【例1】图中的粗线CD表示某条公路的一段,其中AmB是一
段圆弧,AC、BD是线段,且AC、BD分别与 相切于点A、
B,线段AB=180 m,∠ABD=150°.
(1)画出 的圆心O;
(2)求A到B这段弧形公路的长.
【思路点拨】(1)分别过A、B两点作AC、BD的垂线可得解.
(2)由已知条件,得出 所在圆的半径可得解.
弧长的计算
【自主解答】(1)如图,过A作AO⊥AC,过B作BO⊥BD,AO与
BO相交于O,O即为圆心.
说明:若不写作法,必须保留作图痕迹,其他作法略.
(2)∵AO、BO都是 的半径,O是其圆心,
∴∠OBA=∠OAB=150°-90°=60°.
∴△AOB为等边三角形.∴AO=BO=AB=180(m).
∴
∴A到B这段弧形公路的长为60π m.
1.钟表的轴心到分针针端的长为5 cm,那么经过40 min,分针针端转过的弧长是( )
【解析】选B.经过40 min,分针转过的角度为
∴转过的弧长为:
2.一个扇形的圆心角为90°,半径为2,则这个扇形的弧长为_______.(结果保留π)
【解析】根据弧长公式计算:
答案:π
3. 如图,某传送带的一个转动轮的半径为10 cm.
(1)转动轮转一周,传送带上的物品A被传送多少厘米?
(2)转动轮转1°,传送带上的物品A被传送多少厘米?
(3)转动轮转n°,传送带上的物品A被传送多少厘米?
【解析】 (1)转动轮转一周,传送带上的物品A被传送2π×10=20π(厘米);
(2)转动轮转1°,传送带上的物品A被传送
(3)转动轮转n°,传送带上的物品A被传送
扇形及与扇形有关的阴影面积
【例2】(8分)如图,在正方形ABCD中,AB=4,O为对角线BD的中点,分别以OB、OD为直径作⊙O1,⊙O2.
(1)求⊙O1的半径;
(2)求图中阴影部分的面积.
【解题导引】结合勾股定理求解圆的半径;阴影面积的计算,根据图形的对称性,可先计算其四分之一的面积(用扇形的面积减去三角形的面积).
【规范解答】(1)在正方形ABCD中,AB=AD=4,∠A=90°
∴⊙O1的半径为 …………………………………………3分
(2)连接O1E
∵BD为正方形ABCD的对角线,∴∠ABO=45°.
∵O1E=O1B,∴∠BEO1=∠EBO1=45°.
∴∠BO1E=90°……………………………5分
∴
根据图形的对称性得S1=S2=S3=S4
∴S阴影=4S1=2π-4……………………………………………8分
4.如图所示,以六边形的每个顶点为圆心,
1为半径画圆,则图中阴影部分的面积为_____.
【解析】设扇形的圆心角分别为n1°、n2°、n3°、n4°、
n5°、n6°,则n1°+n2°+n3°+n4°+n5°+n6°=720°,所
以阴影部分的面积为
答案:2π
5.如图,两个同心圆被两条半径截得的 的长为6π cm,
的长为10π cm,又AC=12 cm,求阴影部分ABDC的面积.
【解析】设OA=R,OC=R+12,∠O=n°,
根据已知条件有:
∴3(R+12)=5R,∴R=18.
∴OC=18+12=30.
∴
所以阴影部分ABDC的面积为96π cm2.
当所求阴影部分的面积的图形不是规则图形或无法直接求解时,可以通过平移、旋转或通过和、差转化为规则图形的和或差来解决.
1.(2011·潍坊中考)如图,半径为1的小圆在半径为9的大圆内滚动,且始终与大圆相切,则小圆扫过的阴影部分的面积为( )
(A)17π (B)32π
(C)49π (D)80π
【解析】选B.由题意知S阴影=π×92-π×(9-2)2
=81π-49π=32π.
2.已知一条弧的半径为9,弧长为8π,那么这条弧所对的圆
心角为( )
(A)200° (B)160° (C)120° (D)80°
【解析】选B.求圆心角的度数是弧长公式或扇形面积公式
的一种逆用,运用公式时要注意分析公式中的量与已知量
之间的对应关系,对于本题由弧长公式可得
∴n=160,∴这条弧所对的圆心角为160°.
3.如图,在直角三角形ABC中,∠ABC=90°,AC=2,
以点A为圆心,AB为半径画弧,交AC于点D,则阴影部分的
面积是________.
【解析】直角三角形ABC中,∠ABC=90°,
AC=2, 所以
由 得∠A=60°.
所以阴影部分的面积=S△ABC-S扇形ADB=
答案:
4.如图,把Rt△ACB的斜边AB放在定直线l上,按顺时针方向在l上转动两次,使它转到△A″B′C′的位置.设BC=1,∠A=30°,则顶点A运动到点A″的位置时.
(1)求点A经过的路线长是多少?
(2)点A所经过的路线与l所围成的面积是多少?(计算结果不取近似值)
【解析】(1)∵∠A=30°.
∴∠ABC=∠A′BC′=60°,AB=2,
∴∠ABA′=120°.
∴
∴A点经过的路线长为:
(2)S扇形BAA′=
S扇形C′A′A″=
S△A′BC′ =
∴点A经过的路线与l所围成的面积是
(1)已知⊙O的半径为R,1o的圆心角所对的弧长是多少?
A
B
O
R
(2)no的圆心角所对的弧长是多少?
1o的圆心角所对的弧长是
no的圆心角所对的弧长是
弧长公式
若⊙O的半径为R, no的圆心角所对的弧长l 是
练一练:
(1)1o的弧长是 。半径为10厘米
的圆中,60o的圆心角所对的弧长是 厘米
(2)如图,同心圆中,大圆半径OA、OB交小圆于C、D,且OC∶OA=1∶2,则弧CD与弧AB长度之比为( )
O
A
B
C
D
(A)1∶1 (B)1∶2
(C)2∶1 (D)1∶4
B
在一块空旷的草地上有一根柱子,柱子上栓着一条长3m的绳子,绳子的一端栓着一只狗。
(1)这只狗的最大活动区域有多大?
(2)如果这只狗只能绕柱子转过no的角,那么它的最大活动区域有多大?
9πm2
no
在(2)问里狗活动的区域是一个什么图形呢
一条弧和经过这条弧的端点的两条半径所组成的图形叫做扇形
扇形的周长是
2R+L
no
R
R
L
圆的面积是πR2,
那么1o圆心角所对的扇形的面积是
no圆心角所对的扇形的面积是
(2)如果这只狗只能绕柱子转过no的角,那么它的最大活动区域有多大?
弧长公式与扇形的面积公式之间的联系:
(1)当已知弧长L和半径R, 求扇形面积时,应选用
(2)当已知半径和圆心角的度数,求扇形面积时,应选用
例2:已知扇形AOB的半径为12cm,∠AOB=120o,求弧AB的长和扇形AOB的面积.
一个扇形的圆心角为90o,半径为2,
则弧长= ,扇形面积= .
2. 一个扇形的弧长为20πcm,面积是240πc㎡,则该扇形的圆心角为 .
已知扇形的圆心角为120o,半径为6,则扇形的弧长是 ( )
A. 3π B.4π C.5π D.6π
π
π
150o
B
【例1】图中的粗线CD表示某条公路的一段,其中AmB是一
段圆弧,AC、BD是线段,且AC、BD分别与 相切于点A、
B,线段AB=180 m,∠ABD=150°.
(1)画出 的圆心O;
(2)求A到B这段弧形公路的长.
【思路点拨】(1)分别过A、B两点作AC、BD的垂线可得解.
(2)由已知条件,得出 所在圆的半径可得解.
弧长的计算
【自主解答】(1)如图,过A作AO⊥AC,过B作BO⊥BD,AO与
BO相交于O,O即为圆心.
说明:若不写作法,必须保留作图痕迹,其他作法略.
(2)∵AO、BO都是 的半径,O是其圆心,
∴∠OBA=∠OAB=150°-90°=60°.
∴△AOB为等边三角形.∴AO=BO=AB=180(m).
∴
∴A到B这段弧形公路的长为60π m.
1.钟表的轴心到分针针端的长为5 cm,那么经过40 min,分针针端转过的弧长是( )
【解析】选B.经过40 min,分针转过的角度为
∴转过的弧长为:
2.一个扇形的圆心角为90°,半径为2,则这个扇形的弧长为_______.(结果保留π)
【解析】根据弧长公式计算:
答案:π
3. 如图,某传送带的一个转动轮的半径为10 cm.
(1)转动轮转一周,传送带上的物品A被传送多少厘米?
(2)转动轮转1°,传送带上的物品A被传送多少厘米?
(3)转动轮转n°,传送带上的物品A被传送多少厘米?
【解析】 (1)转动轮转一周,传送带上的物品A被传送2π×10=20π(厘米);
(2)转动轮转1°,传送带上的物品A被传送
(3)转动轮转n°,传送带上的物品A被传送
扇形及与扇形有关的阴影面积
【例2】(8分)如图,在正方形ABCD中,AB=4,O为对角线BD的中点,分别以OB、OD为直径作⊙O1,⊙O2.
(1)求⊙O1的半径;
(2)求图中阴影部分的面积.
【解题导引】结合勾股定理求解圆的半径;阴影面积的计算,根据图形的对称性,可先计算其四分之一的面积(用扇形的面积减去三角形的面积).
【规范解答】(1)在正方形ABCD中,AB=AD=4,∠A=90°
∴⊙O1的半径为 …………………………………………3分
(2)连接O1E
∵BD为正方形ABCD的对角线,∴∠ABO=45°.
∵O1E=O1B,∴∠BEO1=∠EBO1=45°.
∴∠BO1E=90°……………………………5分
∴
根据图形的对称性得S1=S2=S3=S4
∴S阴影=4S1=2π-4……………………………………………8分
4.如图所示,以六边形的每个顶点为圆心,
1为半径画圆,则图中阴影部分的面积为_____.
【解析】设扇形的圆心角分别为n1°、n2°、n3°、n4°、
n5°、n6°,则n1°+n2°+n3°+n4°+n5°+n6°=720°,所
以阴影部分的面积为
答案:2π
5.如图,两个同心圆被两条半径截得的 的长为6π cm,
的长为10π cm,又AC=12 cm,求阴影部分ABDC的面积.
【解析】设OA=R,OC=R+12,∠O=n°,
根据已知条件有:
∴3(R+12)=5R,∴R=18.
∴OC=18+12=30.
∴
所以阴影部分ABDC的面积为96π cm2.
当所求阴影部分的面积的图形不是规则图形或无法直接求解时,可以通过平移、旋转或通过和、差转化为规则图形的和或差来解决.
1.(2011·潍坊中考)如图,半径为1的小圆在半径为9的大圆内滚动,且始终与大圆相切,则小圆扫过的阴影部分的面积为( )
(A)17π (B)32π
(C)49π (D)80π
【解析】选B.由题意知S阴影=π×92-π×(9-2)2
=81π-49π=32π.
2.已知一条弧的半径为9,弧长为8π,那么这条弧所对的圆
心角为( )
(A)200° (B)160° (C)120° (D)80°
【解析】选B.求圆心角的度数是弧长公式或扇形面积公式
的一种逆用,运用公式时要注意分析公式中的量与已知量
之间的对应关系,对于本题由弧长公式可得
∴n=160,∴这条弧所对的圆心角为160°.
3.如图,在直角三角形ABC中,∠ABC=90°,AC=2,
以点A为圆心,AB为半径画弧,交AC于点D,则阴影部分的
面积是________.
【解析】直角三角形ABC中,∠ABC=90°,
AC=2, 所以
由 得∠A=60°.
所以阴影部分的面积=S△ABC-S扇形ADB=
答案:
4.如图,把Rt△ACB的斜边AB放在定直线l上,按顺时针方向在l上转动两次,使它转到△A″B′C′的位置.设BC=1,∠A=30°,则顶点A运动到点A″的位置时.
(1)求点A经过的路线长是多少?
(2)点A所经过的路线与l所围成的面积是多少?(计算结果不取近似值)
【解析】(1)∵∠A=30°.
∴∠ABC=∠A′BC′=60°,AB=2,
∴∠ABA′=120°.
∴
∴A点经过的路线长为:
(2)S扇形BAA′=
S扇形C′A′A″=
S△A′BC′ =
∴点A经过的路线与l所围成的面积是
