四年级数学下册教案 二认识三角形和四边形-探索与发现 三角形内角和(试一试)北师大版
文档属性
| 名称 | 四年级数学下册教案 二认识三角形和四边形-探索与发现 三角形内角和(试一试)北师大版 |
|
|
| 格式 | docx | ||
| 文件大小 | 38.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-09 11:41:10 | ||
图片预览

文档简介
课题
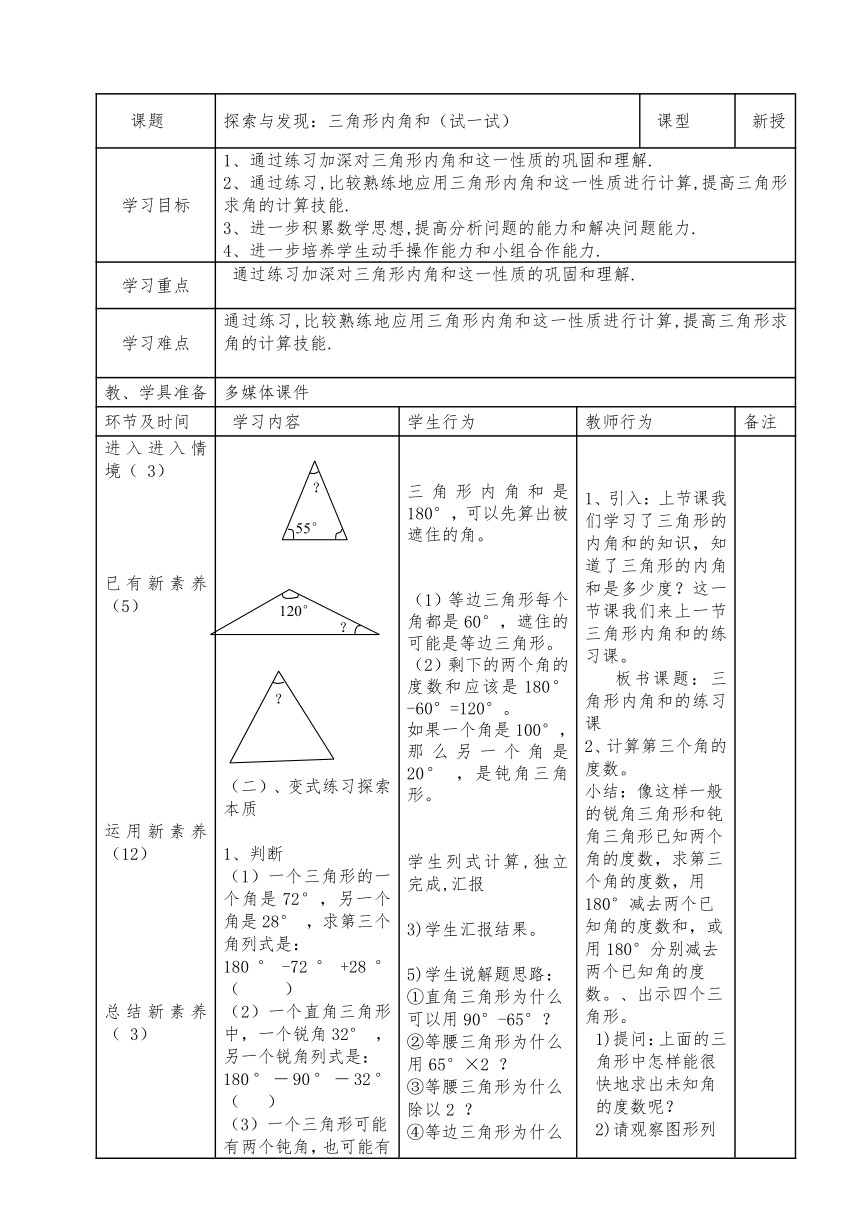
探索与发现:三角形内角和(试一试)
课型
新授
学习目标
1、通过练习加深对三角形内角和这一性质的巩固和理解.
2、通过练习,比较熟练地应用三角形内角和这一性质进行计算,提高三角形求角的计算技能.
3、进一步积累数学思想,提高分析问题的能力和解决问题能力.
4、进一步培养学生动手操作能力和小组合作能力.
学习重点
通过练习加深对三角形内角和这一性质的巩固和理解.
学习难点
通过练习,比较熟练地应用三角形内角和这一性质进行计算,提高三角形求角的计算技能.
教、学具准备
多媒体课件
环节及时间
学习内容
学生行为
教师行为
备注
进入进入情境( 3)
已有新素养(5)
运用新素养(12)
总结新素养( 3)
强化新素养(10)
课堂小结(2)
完成作业
5194291460555°
?
55°
?
-112394155574120°
?
120°
?
4508480010?
?
(二)、变式练习探索本质
1、判断
(1)一个三角形的一个角是72°,另一个角是28° ,求第三个角列式是:
180°-72°+28° ( )
(2)一个直角三角形中,一个锐角32° ,另一个锐角列式是:
180°-90°-32° ( )
(3)一个三角形可能有两个钝角,也可能有两个直角。( )
2、填空:
(1)等边三角形的每一个内角都是( )度。
(2)一个等腰直角三角形的其中一个底角是( )度。
(3)直角三角形中的两个锐角可能是( )度和( )度。
三角形内角和是180°,可以先算出被遮住的角。
(1)等边三角形每个角都是60°,遮住的可能是等边三角形。
(2)剩下的两个角的度数和应该是180°-60°=120°。
如果一个角是100°,那么另一个角是20° ,是钝角三角形。
学生列式计算,独立完成,汇报
3)学生汇报结果。
5)学生说解题思路:
①直角三角形为什么可以用90°-65°?
②等腰三角形为什么用65°×2 ?
③等腰三角形为什么除以2 ?
④等边三角形为什么用180°÷3 ?
《数学能力培养》
1、引入:上节课我们学习了三角形的内角和的知识,知道了三角形的内角和是多少度?这一节课我们来上一节三角形内角和的练习课。
板书课题:三角形内角和的练习课
2、计算第三个角的度数。
小结:像这样一般的锐角三角形和钝角三角形已知两个角的度数,求第三个角的度数,用180°减去两个已知角的度数和,或用180°分别减去两个已知角的度数。、出示四个三角形。
1)提问:上面的三角形中怎样能很快地求出未知角的度数呢?
2)请观察图形列式计算。
4)结合图形说说为什么这样计算?
4160520179070410337080010小结:求三角形未知角的度数,先要分析这个三角形已知什么条件,再采用合理的方法进行计算。
提问:他们的说法对吗?我们来用小棒摆一摆,验证一下。
提问:还有其他的填法吗?
小结:直角三角形的两个锐角和是90°。
你能求出长方形和正方形的内角和吗?
用什么方法求内角和?
板书设计
三角形内角和的练习课
180°-60°-40°=80° 180°-60°=120°
探索与发现:三角形内角和(试一试)
课型
新授
学习目标
1、通过练习加深对三角形内角和这一性质的巩固和理解.
2、通过练习,比较熟练地应用三角形内角和这一性质进行计算,提高三角形求角的计算技能.
3、进一步积累数学思想,提高分析问题的能力和解决问题能力.
4、进一步培养学生动手操作能力和小组合作能力.
学习重点
通过练习加深对三角形内角和这一性质的巩固和理解.
学习难点
通过练习,比较熟练地应用三角形内角和这一性质进行计算,提高三角形求角的计算技能.
教、学具准备
多媒体课件
环节及时间
学习内容
学生行为
教师行为
备注
进入进入情境( 3)
已有新素养(5)
运用新素养(12)
总结新素养( 3)
强化新素养(10)
课堂小结(2)
完成作业
5194291460555°
?
55°
?
-112394155574120°
?
120°
?
4508480010?
?
(二)、变式练习探索本质
1、判断
(1)一个三角形的一个角是72°,另一个角是28° ,求第三个角列式是:
180°-72°+28° ( )
(2)一个直角三角形中,一个锐角32° ,另一个锐角列式是:
180°-90°-32° ( )
(3)一个三角形可能有两个钝角,也可能有两个直角。( )
2、填空:
(1)等边三角形的每一个内角都是( )度。
(2)一个等腰直角三角形的其中一个底角是( )度。
(3)直角三角形中的两个锐角可能是( )度和( )度。
三角形内角和是180°,可以先算出被遮住的角。
(1)等边三角形每个角都是60°,遮住的可能是等边三角形。
(2)剩下的两个角的度数和应该是180°-60°=120°。
如果一个角是100°,那么另一个角是20° ,是钝角三角形。
学生列式计算,独立完成,汇报
3)学生汇报结果。
5)学生说解题思路:
①直角三角形为什么可以用90°-65°?
②等腰三角形为什么用65°×2 ?
③等腰三角形为什么除以2 ?
④等边三角形为什么用180°÷3 ?
《数学能力培养》
1、引入:上节课我们学习了三角形的内角和的知识,知道了三角形的内角和是多少度?这一节课我们来上一节三角形内角和的练习课。
板书课题:三角形内角和的练习课
2、计算第三个角的度数。
小结:像这样一般的锐角三角形和钝角三角形已知两个角的度数,求第三个角的度数,用180°减去两个已知角的度数和,或用180°分别减去两个已知角的度数。、出示四个三角形。
1)提问:上面的三角形中怎样能很快地求出未知角的度数呢?
2)请观察图形列式计算。
4)结合图形说说为什么这样计算?
4160520179070410337080010小结:求三角形未知角的度数,先要分析这个三角形已知什么条件,再采用合理的方法进行计算。
提问:他们的说法对吗?我们来用小棒摆一摆,验证一下。
提问:还有其他的填法吗?
小结:直角三角形的两个锐角和是90°。
你能求出长方形和正方形的内角和吗?
用什么方法求内角和?
板书设计
三角形内角和的练习课
180°-60°-40°=80° 180°-60°=120°
