专家解读2021年八省联考 预测新高考考向(共46张PPT)
文档属性
| 名称 | 专家解读2021年八省联考 预测新高考考向(共46张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 5.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-19 10:02:24 | ||
图片预览








文档简介
(共46张PPT)
八省市新高考适应性考试分析
暨精准备考指导
(数
学)
讲师:特级教师秦喆
目录
1
八省市适应性考题与2020新旧高考试题的变化精析
2
2021年新高考数学备考关键阶段的应考策略
3
2021年新高考数学考向创新点预测
一、试题体现了“低起点、多层次、高落差”的调控策略,表现在:
第一、四个台阶均遵循起点低、入口宽,渐次提升的规律,减少繁杂的计算,突出数学思维,凸显考查数学知识的宽度(开放性)和扎实程度;
第二、“多层次”体现在试题难度设计上重视思维的层次性;
第三、“高落差”体现在重视数学科的选拔功能,在综合性、创新性展现。
如第20题,在高中体现高等数学微分几何,考察空间弯曲性---“曲率”
全国八省市适应性考试试题的总体评价
二、突出数学理性思维和探究能力考察,注重数学思想与通性通法
突出数学基本思想与方法,重在理性思维考察,融合算法算理如第10、13题,突出数形结合思想的养成,如第8、12题,体现了构造法、导数法等,数学直观与数学抽象,如第11题。
数列题源自课本(人教版必修5第69页复习参考题B组第6题),导向明确;导数题回归压轴,比较常规,圆锥曲线用了双曲线为背景,但解法上没有特殊之处。值得探讨的是第18、20、21题。
全国八省市适应性考试试题总体评价
全国八省市适应性考试试题总体评价
三、落实了高考评价体系的要求,创新点凸显
对数学应用意识的考察保持平稳,阅读量看似减少,但阅读难度并未降低,在审题上,对考生的阅读、观察,对“四基”“四能”的设计方案要求较高(比如第20题),压轴题回归传统。概括有四大变化:
1、填空题出现了不确定性答案填空,如第15题;
2、多选题分数结构有调整,部分选对只得2分!增加了得分难度;
3、考点调整,第21题解析几何题考了“双曲线”;
4、第20题立体几何背景及考点令人耳目一新。以大兴机场建设成就、大学微分几何为背景,考察新定义”空间弯曲性”---“曲率”,对阅读理解要求较高,最为亮点。
全国八省市适应性考试试题总体评价
四、对探索新高考的新模式起到了推动作用
试题体现了新课改精神,知识范围进一步拓宽,数学思维能力要求陡增,对培养学生的创新应用意识起到积极引导作用,对探索新高考的新模式起到了推动作用,为后期新高考省份的复习提供了一些新的方向和启发。不改变机械的备考方式很难培养出国家未来所需要的基础型人才!
2021/5/18
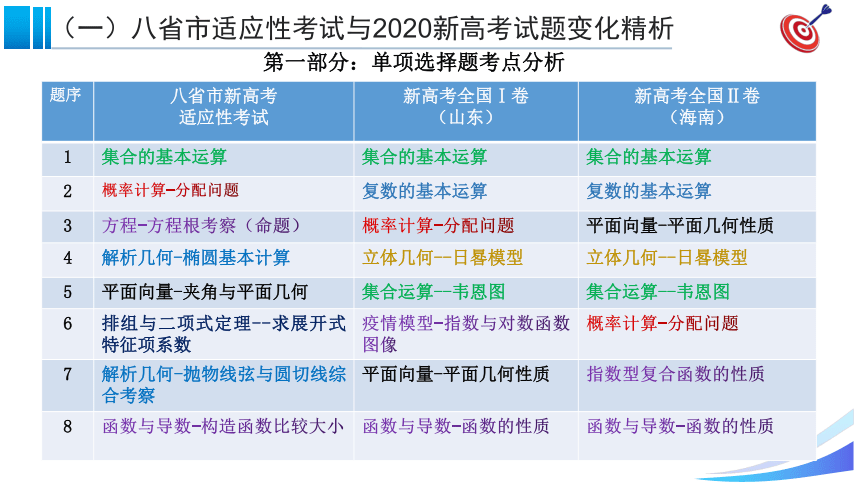
第一部分:单项选择题考点分析
题序
八省市新高考
适应性考试
新高考全国Ⅰ卷
(山东)
新高考全国Ⅱ卷
(海南)
1
集合的基本运算
集合的基本运算
集合的基本运算
2
概率计算-分配问题
复数的基本运算
复数的基本运算
3
方程-方程根考察(命题)
概率计算-分配问题
平面向量-平面几何性质
4
解析几何-椭圆基本计算
立体几何--日晷模型
立体几何--日晷模型
5
平面向量-夹角与平面几何
集合运算--韦恩图
集合运算--韦恩图
6
排组与二项式定理--求展开式特征项系数
疫情模型-指数与对数函数图像
概率计算-分配问题
7
解析几何-抛物线弦与圆切线综合考察
平面向量-平面几何性质
指数型复合函数的性质
8
函数与导数-构造函数比较大小
函数与导数-函数的性质
函数与导数-函数的性质
2021/5/18
第二部分:多项选择题考点分析
题序
八省市新高考
适应性考试
新高考全国Ⅰ卷
(山东)
新高考全国Ⅱ卷(海南)
9
函数与导数--应用导数判定函数性质
解析几何-双曲线的简单性质
疫情模型-折线图
10
复数--复数模的基本运算
三角函数-三角函数的图像
解析几何-双曲线的简单性质
11
立体几何--正方体侧面展开图考察
不等式-基本不等式的应用
三角函数-三角函数的图像
12
三角与导数--导数与三角函数性质
信息熵背景-对数运算及不等式的基本性质
不等式-基本不等式的应用
2021/5/18
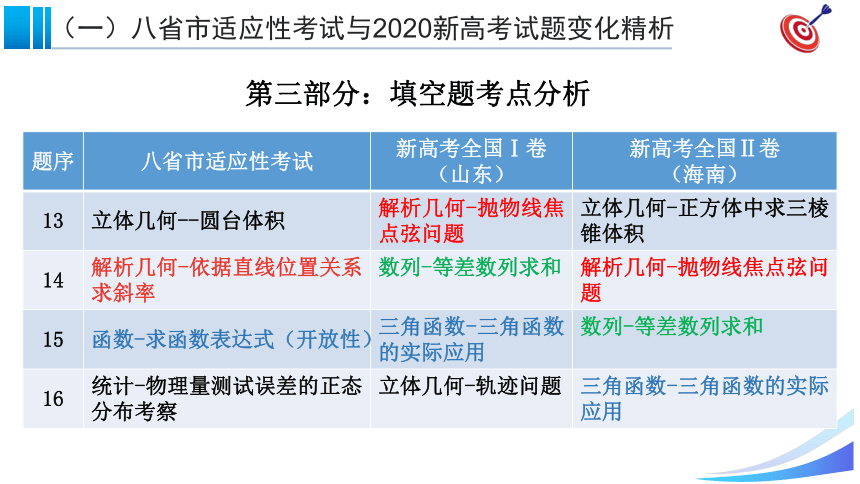
第三部分:填空题考点分析
题序
八省市适应性考试
新高考全国Ⅰ卷(山东)
新高考全国Ⅱ卷
(海南)
13
立体几何--圆台体积
解析几何-抛物线焦点弦问题
立体几何-正方体中求三棱锥体积
14
解析几何-依据直线位置关系求斜率
数列-等差数列求和
解析几何-抛物线焦点弦问题
15
函数-求函数表达式(开放性)
三角函数-三角函数的实际应用
数列-等差数列求和
16
统计-物理量测试误差的正态分布考察
立体几何-轨迹问题
三角函数-三角函数的实际应用
八省市新高考适应性考试
第7题
新高考全国Ⅰ卷(山东)第9、13题
设而不解的解题思路
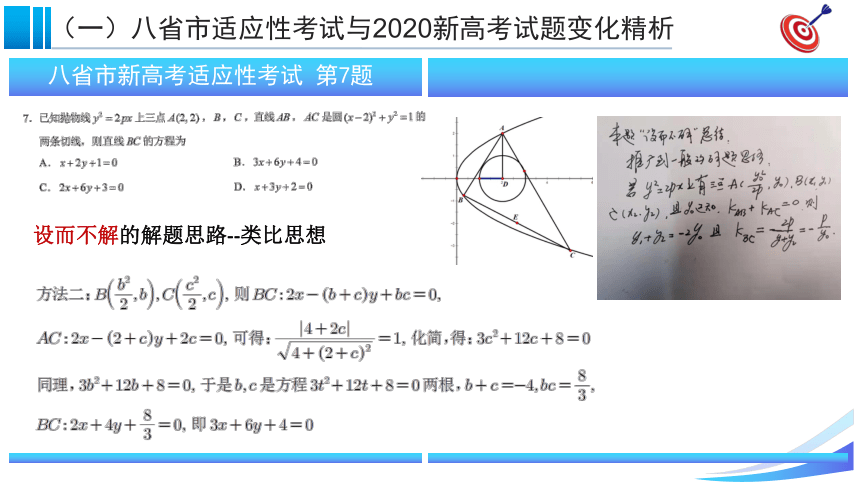
八省市新高考适应性考试
第7题
设而不解的解题思路--类比思想
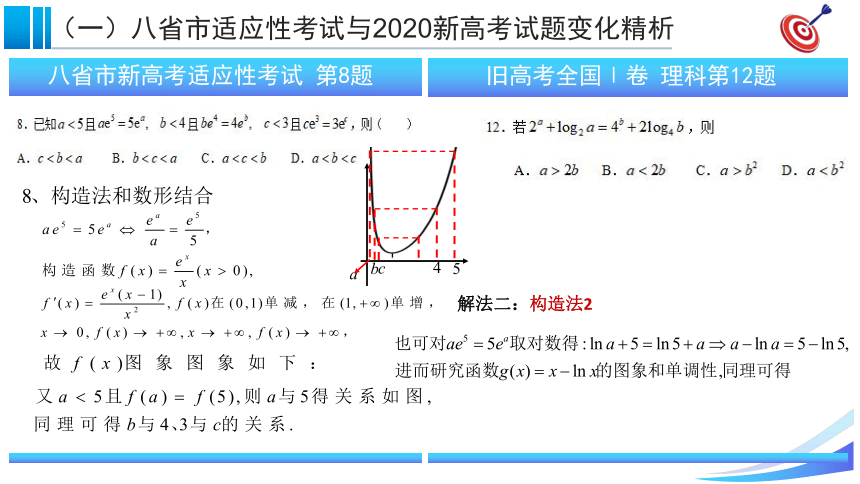
八省市新高考适应性考试
第8题
旧高考全国Ⅰ卷
理科第12题
解法二:构造法2
八省市新高考适应性考试
第9,12题
2020新高考全国Ⅰ卷
第8,12题
八省市新高考适应性考试
第9,12题
八省市新高考适应性考试
第9,12题
八省市新高考适应性考试
填空题
新高考全国Ⅰ卷(山东)第16题
第四部分:解答题考点分析
题序
八省市适应性考试
新高考全国Ⅰ卷(山东)
新高考全国Ⅱ卷(海南)
17
数列---递归数列与新数列考察
三角函数-正余弦定理的应用
三角函数-正余弦定理的应用
18
平面几何与解三角形
数列-等比数列及其求和
数列-等比数列及其求和(与山东卷部分相同)
19
概率统计--相互独立概率与分布列、期望
概率统计-古典概型与独立性检验
概率统计-古典概型与独立性检验
20
立体几何--考察新定义题,空间弯曲性-“曲率”
立体几何-线面垂直及直线与平面所成角正弦值的最大值
立体几何-线面垂直及直线与平面所成角的正弦值(与山东卷姊妹题)
21
解析几何--求双曲线离心率、证明倍角等式
函数与导数-导数的几何意义与参数取值范围问题
解析几何-直线与椭圆的综合(最值问题)
22
三角函数为背景的导数证明和求参数问题
解析几何-直线与椭圆的综合(定值问题)
函数与导数-导数的几何意义与参数取值范围问题
八省市新高考适应性考试
第17题
新高考全国Ⅰ卷(山东)
第18题
八省市新高考适应性考试
第17题
新高考全国Ⅰ卷(山东)
第18题
八省市新高考适应性考试
第18题
新高考全国Ⅰ卷(山东)
第17题
八省市新高考适应性考试
第21题
新高考全国Ⅰ卷(山东)
第22题
八省市新高考适应性考试
第20题
新高考全国Ⅰ卷(山东)
第3题
2020年新高考Ⅱ卷(海南)
第20题知识源头探秘:《全日制十年制高中课本》(数学
2)
5.28
多面体的变形
(第94页)
欧拉定理:
简单多面体的顶点数V、棱数E、面数F,有以下关系:V+F-E=2
八省市新高考适应性考试
第20题
试题分析
案例分享:师生共探究
八省市新高考适应性考试
第22题
2020年新旧高考全国Ⅰ卷
第21题
八省市新高考适应性考试
第22题
八省市新高考适应性考试
第5题
山东高考(第21题)
八省市新高考适应性考试
第5题
山东高考(第21题)
试题
函数模型
2019年全国Ⅰ卷
2018年全国Ⅰ卷
2017年全国Ⅰ卷
2016年全国Ⅰ卷
2015年全国Ⅰ卷
近2015-2019年全国卷理科导数题函数模型
目录
1
八省市适应性考题与新旧高考数学试题的变化精析
2
2021年新高考数学关键阶段的应考策略
3
2021年新高考数学考向创新点预测
1.任何阶段都不建议脱离课本,要突出思维迁移;
2.对照新课标,深度研究高考真题,控制好难度.
深研新课标,做好课本题、高考真题及其思维迁移,发挥其引领作用!
策略一:
教学建议:
对照新课标案例1:一元函数导数及其应用
内容
新课标
旧课标
区别
(1)导数的概念及其意义
1.通过实例分析,经历由平均变化率过渡到瞬时变化率的过程,了解导数概念的实际背景,知道导数是关于瞬时变化率的数学表达,体会导数的内涵与思想;
2.体会极限思想;
3.通过函数图象直观理解导数的几何意义。
1.通过对大量实例的分析,经历由平均变化率过渡到瞬时变化率的过程,了解导数概念的实际背景,知道瞬时变化率就是导数,体会导数的思想及其内涵;
2.通过函数图象直观理解导数的几何意义。
新课标增加了对极限思想的体会,初步感悟极限思想,而旧课标没有涉及。
内容
新课标
旧课标
区别
(1)导数的运算
1.能根据导数定义求函数
2.能利用给出的基本初等函数的导数公式和导数的四则运算法则,求简单函数的导数;能求简单的复合函数(限于形如f(ax+b))的导数;
3.会使用导数公式表。
1.(选修1-1)能根据导数定义,求函数
(选修2-2)能根据导数定义求函数
2.(选修1-1)能利用给出的基本初等函数的导数公式和导数的四则运算法则求简单函数的导数;
(选修2-2)能利用给出的基本初等函数的导数公式和导数的四则运算法则,求简单函数的导数;能求简单的复合函数(限于形如f(ax+b)的导数;
3.会使用导数公式表。
新课标不分文理,对函数
要求能根据导数定义求它的导数,对求简单的复合函数的导数有明确规定(限于形如f(ax+b)),相当于增加了旧课标中选修1-1的内容,保持旧课标选修2-2的要求。
对照新课标案例1:一元函数导数及其应用
内容
新课标
旧课标
区别
(2)导数在研究函数中的应用
1.结合实例,借助几何直观了解函数的单调性与导数的关系;能利用导数研究函数的单调性;对于多项式函数,能求不超过三次的多项式函数的单调区间;
2.借助函数的图象,了解函数在某点取得极值的必要条件和充分条件;能利用导数求某些函数的极大值、极小值以及给定闭区间上不超过三次的多项式函数的最大值、最小值;体会导数与单调性、极值、最值的关系。
1.结合实例,借助几何直观探索并了解函数的单调性与导数的关系;能利用导数研究函数的单调性,会求不超过三次的多项式函数的单调区间;
2.(选修1-1)结合函数的图象。了解函数在某点取得极值的必要条件和充分条件;会利用导数求不超过三次的多项式函数的极大值、极小值,以及闭区间上不超过三次的多项式函数最大值、最小值;
(选修2-2)结合函数的图象。了解函数在某点取得极值的必要条件和充分条件;会利用导数求不超过三次的多项式函数的极大值、极小值,以及闭区间上不超过三次的多项式函数最大值、最小值。
体会导数方法在研究函数性质中的一般性和有效性。
旧课标明确提出了会利用导数求不超过三次的多项式函数的极大值、极小值,而新课标并没有对函数的类型进行限定,对利用导数研究函数的要求提高了;
新课标删除了在教学上不易操作的部分:对导数方法在研究函数性质中的一般性和有效性的体会要求。
对照新课标案例1:一元函数导数及其应用
:
案例3:现行课本中的数学文化:
教材
数学文化
必修一
函数概念的发展历程P26,对数的发明
P68
中外史上的方程求解P91
必修二
画法几何与蒙日
P22,
祖暅原理与柱体、椎体、球体的体积
P30
欧几里得《原本》与公理化方法
P74,笛卡尔与解析几何
P111,
坐标法与机器证明(吴文俊)
P124
必修三
割圆术
P45,天气变化的认识过程
P122
必修四
三角学与天文学P17,向量及向量符号的由来P78
必修五
海伦和秦九韶P21,斐波那契数列P32,九连环P59
2—1
为什么截口曲线是椭圆P42
2—2
代数基本定理P113
2—3
“杨辉三角”中的一些秘密P35
2、数学思维是提升数学能力的关键,抓好课堂、试卷讲评
1、重数学思维能力培养,就要渗透数学思想与通性通法
抓好教研,聚焦课堂,突破关键能力的提升
策略二:
教学建议:
阅读能力、思考能力和表达能力是学生的三大核心能力
教师是备考成功的主要矛盾,教师应有的主动权:
精心设计———焦点在学生认知能力
因材施教———学生是变化的鲜活的
分类推进———承认差异,没有差生
整体提高———分类推进,榜样作用
法无定法,在于因时因势!充分发挥学习小组的作用!
突出试卷讲评课的三点要求
1.突出核心考点,深研解决方案;
2.师生面批面改,细化提分空间;
3.考后满分,哪跌哪起
重视数学阅读,贯穿数学文化,突破数学应用瓶颈
策略三:
教学建议:
1、创造条件,给学生阅读空间
四基、四能—核心在于活动平台,从观念上改变过度(刻意挖掘深度)的机械性训练,突出现实情境、数学情境、科学情境背景下的数学训练;
2、重视基本综合能力,从选题、命题到考后评价紧紧围绕“体系”
突出基本能力,不搞“偏、难、怪”的原则;
重视考察基础性、综合性;
从阅读(知识迁移)到文理综合,到创新等层面进行能力培养。
备考成功的关键在于
1
3
5
聚焦思维训练
把握命题方向
因材施教备考
目录
1
八省市适应性考题与新旧高考数学试题的变化精析
2
2021年新高考数学关键阶段的应考策略
3
2021年新高考数学考向创新点预测
预测1、新高考基于数学核心素养的命题原则
1、围绕数学的核心概念;突出数学的通性通法;设计真实的情境;
2、关注数学的本源性问题(数学的生长点)和有意义的问题(蕴含数学概念或思想方法);
3、新定义考察成稳定状态,考察范围更加宽泛,创新点不仅在试题形式上,在内容、解法以及结论等都可能创新。
预测2、淡化压轴思想,做好“不变”的,研究“可变的”
1、课本(关注传统课本)及课标(解读)是试题创新的基本来源;
2、历届高考真题成为高考备考的绝好材料;
3、高等数学及国内外竞赛试题的基本思想、基本问题或为高考题的命制提供素材;
4、难度把控趋于稳定,基本控制在0.55左右,训练不必担心难度上不去;
预测3、试题创新基于问题情境、数学文化背景
数学核心素养与高考备考
考什么?
怎么考?
怎么办?
---
交流与提升
---
八省市新高考适应性考试分析
暨精准备考指导
(数
学)
讲师:特级教师秦喆
目录
1
八省市适应性考题与2020新旧高考试题的变化精析
2
2021年新高考数学备考关键阶段的应考策略
3
2021年新高考数学考向创新点预测
一、试题体现了“低起点、多层次、高落差”的调控策略,表现在:
第一、四个台阶均遵循起点低、入口宽,渐次提升的规律,减少繁杂的计算,突出数学思维,凸显考查数学知识的宽度(开放性)和扎实程度;
第二、“多层次”体现在试题难度设计上重视思维的层次性;
第三、“高落差”体现在重视数学科的选拔功能,在综合性、创新性展现。
如第20题,在高中体现高等数学微分几何,考察空间弯曲性---“曲率”
全国八省市适应性考试试题的总体评价
二、突出数学理性思维和探究能力考察,注重数学思想与通性通法
突出数学基本思想与方法,重在理性思维考察,融合算法算理如第10、13题,突出数形结合思想的养成,如第8、12题,体现了构造法、导数法等,数学直观与数学抽象,如第11题。
数列题源自课本(人教版必修5第69页复习参考题B组第6题),导向明确;导数题回归压轴,比较常规,圆锥曲线用了双曲线为背景,但解法上没有特殊之处。值得探讨的是第18、20、21题。
全国八省市适应性考试试题总体评价
全国八省市适应性考试试题总体评价
三、落实了高考评价体系的要求,创新点凸显
对数学应用意识的考察保持平稳,阅读量看似减少,但阅读难度并未降低,在审题上,对考生的阅读、观察,对“四基”“四能”的设计方案要求较高(比如第20题),压轴题回归传统。概括有四大变化:
1、填空题出现了不确定性答案填空,如第15题;
2、多选题分数结构有调整,部分选对只得2分!增加了得分难度;
3、考点调整,第21题解析几何题考了“双曲线”;
4、第20题立体几何背景及考点令人耳目一新。以大兴机场建设成就、大学微分几何为背景,考察新定义”空间弯曲性”---“曲率”,对阅读理解要求较高,最为亮点。
全国八省市适应性考试试题总体评价
四、对探索新高考的新模式起到了推动作用
试题体现了新课改精神,知识范围进一步拓宽,数学思维能力要求陡增,对培养学生的创新应用意识起到积极引导作用,对探索新高考的新模式起到了推动作用,为后期新高考省份的复习提供了一些新的方向和启发。不改变机械的备考方式很难培养出国家未来所需要的基础型人才!
2021/5/18
第一部分:单项选择题考点分析
题序
八省市新高考
适应性考试
新高考全国Ⅰ卷
(山东)
新高考全国Ⅱ卷
(海南)
1
集合的基本运算
集合的基本运算
集合的基本运算
2
概率计算-分配问题
复数的基本运算
复数的基本运算
3
方程-方程根考察(命题)
概率计算-分配问题
平面向量-平面几何性质
4
解析几何-椭圆基本计算
立体几何--日晷模型
立体几何--日晷模型
5
平面向量-夹角与平面几何
集合运算--韦恩图
集合运算--韦恩图
6
排组与二项式定理--求展开式特征项系数
疫情模型-指数与对数函数图像
概率计算-分配问题
7
解析几何-抛物线弦与圆切线综合考察
平面向量-平面几何性质
指数型复合函数的性质
8
函数与导数-构造函数比较大小
函数与导数-函数的性质
函数与导数-函数的性质
2021/5/18
第二部分:多项选择题考点分析
题序
八省市新高考
适应性考试
新高考全国Ⅰ卷
(山东)
新高考全国Ⅱ卷(海南)
9
函数与导数--应用导数判定函数性质
解析几何-双曲线的简单性质
疫情模型-折线图
10
复数--复数模的基本运算
三角函数-三角函数的图像
解析几何-双曲线的简单性质
11
立体几何--正方体侧面展开图考察
不等式-基本不等式的应用
三角函数-三角函数的图像
12
三角与导数--导数与三角函数性质
信息熵背景-对数运算及不等式的基本性质
不等式-基本不等式的应用
2021/5/18
第三部分:填空题考点分析
题序
八省市适应性考试
新高考全国Ⅰ卷(山东)
新高考全国Ⅱ卷
(海南)
13
立体几何--圆台体积
解析几何-抛物线焦点弦问题
立体几何-正方体中求三棱锥体积
14
解析几何-依据直线位置关系求斜率
数列-等差数列求和
解析几何-抛物线焦点弦问题
15
函数-求函数表达式(开放性)
三角函数-三角函数的实际应用
数列-等差数列求和
16
统计-物理量测试误差的正态分布考察
立体几何-轨迹问题
三角函数-三角函数的实际应用
八省市新高考适应性考试
第7题
新高考全国Ⅰ卷(山东)第9、13题
设而不解的解题思路
八省市新高考适应性考试
第7题
设而不解的解题思路--类比思想
八省市新高考适应性考试
第8题
旧高考全国Ⅰ卷
理科第12题
解法二:构造法2
八省市新高考适应性考试
第9,12题
2020新高考全国Ⅰ卷
第8,12题
八省市新高考适应性考试
第9,12题
八省市新高考适应性考试
第9,12题
八省市新高考适应性考试
填空题
新高考全国Ⅰ卷(山东)第16题
第四部分:解答题考点分析
题序
八省市适应性考试
新高考全国Ⅰ卷(山东)
新高考全国Ⅱ卷(海南)
17
数列---递归数列与新数列考察
三角函数-正余弦定理的应用
三角函数-正余弦定理的应用
18
平面几何与解三角形
数列-等比数列及其求和
数列-等比数列及其求和(与山东卷部分相同)
19
概率统计--相互独立概率与分布列、期望
概率统计-古典概型与独立性检验
概率统计-古典概型与独立性检验
20
立体几何--考察新定义题,空间弯曲性-“曲率”
立体几何-线面垂直及直线与平面所成角正弦值的最大值
立体几何-线面垂直及直线与平面所成角的正弦值(与山东卷姊妹题)
21
解析几何--求双曲线离心率、证明倍角等式
函数与导数-导数的几何意义与参数取值范围问题
解析几何-直线与椭圆的综合(最值问题)
22
三角函数为背景的导数证明和求参数问题
解析几何-直线与椭圆的综合(定值问题)
函数与导数-导数的几何意义与参数取值范围问题
八省市新高考适应性考试
第17题
新高考全国Ⅰ卷(山东)
第18题
八省市新高考适应性考试
第17题
新高考全国Ⅰ卷(山东)
第18题
八省市新高考适应性考试
第18题
新高考全国Ⅰ卷(山东)
第17题
八省市新高考适应性考试
第21题
新高考全国Ⅰ卷(山东)
第22题
八省市新高考适应性考试
第20题
新高考全国Ⅰ卷(山东)
第3题
2020年新高考Ⅱ卷(海南)
第20题知识源头探秘:《全日制十年制高中课本》(数学
2)
5.28
多面体的变形
(第94页)
欧拉定理:
简单多面体的顶点数V、棱数E、面数F,有以下关系:V+F-E=2
八省市新高考适应性考试
第20题
试题分析
案例分享:师生共探究
八省市新高考适应性考试
第22题
2020年新旧高考全国Ⅰ卷
第21题
八省市新高考适应性考试
第22题
八省市新高考适应性考试
第5题
山东高考(第21题)
八省市新高考适应性考试
第5题
山东高考(第21题)
试题
函数模型
2019年全国Ⅰ卷
2018年全国Ⅰ卷
2017年全国Ⅰ卷
2016年全国Ⅰ卷
2015年全国Ⅰ卷
近2015-2019年全国卷理科导数题函数模型
目录
1
八省市适应性考题与新旧高考数学试题的变化精析
2
2021年新高考数学关键阶段的应考策略
3
2021年新高考数学考向创新点预测
1.任何阶段都不建议脱离课本,要突出思维迁移;
2.对照新课标,深度研究高考真题,控制好难度.
深研新课标,做好课本题、高考真题及其思维迁移,发挥其引领作用!
策略一:
教学建议:
对照新课标案例1:一元函数导数及其应用
内容
新课标
旧课标
区别
(1)导数的概念及其意义
1.通过实例分析,经历由平均变化率过渡到瞬时变化率的过程,了解导数概念的实际背景,知道导数是关于瞬时变化率的数学表达,体会导数的内涵与思想;
2.体会极限思想;
3.通过函数图象直观理解导数的几何意义。
1.通过对大量实例的分析,经历由平均变化率过渡到瞬时变化率的过程,了解导数概念的实际背景,知道瞬时变化率就是导数,体会导数的思想及其内涵;
2.通过函数图象直观理解导数的几何意义。
新课标增加了对极限思想的体会,初步感悟极限思想,而旧课标没有涉及。
内容
新课标
旧课标
区别
(1)导数的运算
1.能根据导数定义求函数
2.能利用给出的基本初等函数的导数公式和导数的四则运算法则,求简单函数的导数;能求简单的复合函数(限于形如f(ax+b))的导数;
3.会使用导数公式表。
1.(选修1-1)能根据导数定义,求函数
(选修2-2)能根据导数定义求函数
2.(选修1-1)能利用给出的基本初等函数的导数公式和导数的四则运算法则求简单函数的导数;
(选修2-2)能利用给出的基本初等函数的导数公式和导数的四则运算法则,求简单函数的导数;能求简单的复合函数(限于形如f(ax+b)的导数;
3.会使用导数公式表。
新课标不分文理,对函数
要求能根据导数定义求它的导数,对求简单的复合函数的导数有明确规定(限于形如f(ax+b)),相当于增加了旧课标中选修1-1的内容,保持旧课标选修2-2的要求。
对照新课标案例1:一元函数导数及其应用
内容
新课标
旧课标
区别
(2)导数在研究函数中的应用
1.结合实例,借助几何直观了解函数的单调性与导数的关系;能利用导数研究函数的单调性;对于多项式函数,能求不超过三次的多项式函数的单调区间;
2.借助函数的图象,了解函数在某点取得极值的必要条件和充分条件;能利用导数求某些函数的极大值、极小值以及给定闭区间上不超过三次的多项式函数的最大值、最小值;体会导数与单调性、极值、最值的关系。
1.结合实例,借助几何直观探索并了解函数的单调性与导数的关系;能利用导数研究函数的单调性,会求不超过三次的多项式函数的单调区间;
2.(选修1-1)结合函数的图象。了解函数在某点取得极值的必要条件和充分条件;会利用导数求不超过三次的多项式函数的极大值、极小值,以及闭区间上不超过三次的多项式函数最大值、最小值;
(选修2-2)结合函数的图象。了解函数在某点取得极值的必要条件和充分条件;会利用导数求不超过三次的多项式函数的极大值、极小值,以及闭区间上不超过三次的多项式函数最大值、最小值。
体会导数方法在研究函数性质中的一般性和有效性。
旧课标明确提出了会利用导数求不超过三次的多项式函数的极大值、极小值,而新课标并没有对函数的类型进行限定,对利用导数研究函数的要求提高了;
新课标删除了在教学上不易操作的部分:对导数方法在研究函数性质中的一般性和有效性的体会要求。
对照新课标案例1:一元函数导数及其应用
:
案例3:现行课本中的数学文化:
教材
数学文化
必修一
函数概念的发展历程P26,对数的发明
P68
中外史上的方程求解P91
必修二
画法几何与蒙日
P22,
祖暅原理与柱体、椎体、球体的体积
P30
欧几里得《原本》与公理化方法
P74,笛卡尔与解析几何
P111,
坐标法与机器证明(吴文俊)
P124
必修三
割圆术
P45,天气变化的认识过程
P122
必修四
三角学与天文学P17,向量及向量符号的由来P78
必修五
海伦和秦九韶P21,斐波那契数列P32,九连环P59
2—1
为什么截口曲线是椭圆P42
2—2
代数基本定理P113
2—3
“杨辉三角”中的一些秘密P35
2、数学思维是提升数学能力的关键,抓好课堂、试卷讲评
1、重数学思维能力培养,就要渗透数学思想与通性通法
抓好教研,聚焦课堂,突破关键能力的提升
策略二:
教学建议:
阅读能力、思考能力和表达能力是学生的三大核心能力
教师是备考成功的主要矛盾,教师应有的主动权:
精心设计———焦点在学生认知能力
因材施教———学生是变化的鲜活的
分类推进———承认差异,没有差生
整体提高———分类推进,榜样作用
法无定法,在于因时因势!充分发挥学习小组的作用!
突出试卷讲评课的三点要求
1.突出核心考点,深研解决方案;
2.师生面批面改,细化提分空间;
3.考后满分,哪跌哪起
重视数学阅读,贯穿数学文化,突破数学应用瓶颈
策略三:
教学建议:
1、创造条件,给学生阅读空间
四基、四能—核心在于活动平台,从观念上改变过度(刻意挖掘深度)的机械性训练,突出现实情境、数学情境、科学情境背景下的数学训练;
2、重视基本综合能力,从选题、命题到考后评价紧紧围绕“体系”
突出基本能力,不搞“偏、难、怪”的原则;
重视考察基础性、综合性;
从阅读(知识迁移)到文理综合,到创新等层面进行能力培养。
备考成功的关键在于
1
3
5
聚焦思维训练
把握命题方向
因材施教备考
目录
1
八省市适应性考题与新旧高考数学试题的变化精析
2
2021年新高考数学关键阶段的应考策略
3
2021年新高考数学考向创新点预测
预测1、新高考基于数学核心素养的命题原则
1、围绕数学的核心概念;突出数学的通性通法;设计真实的情境;
2、关注数学的本源性问题(数学的生长点)和有意义的问题(蕴含数学概念或思想方法);
3、新定义考察成稳定状态,考察范围更加宽泛,创新点不仅在试题形式上,在内容、解法以及结论等都可能创新。
预测2、淡化压轴思想,做好“不变”的,研究“可变的”
1、课本(关注传统课本)及课标(解读)是试题创新的基本来源;
2、历届高考真题成为高考备考的绝好材料;
3、高等数学及国内外竞赛试题的基本思想、基本问题或为高考题的命制提供素材;
4、难度把控趋于稳定,基本控制在0.55左右,训练不必担心难度上不去;
预测3、试题创新基于问题情境、数学文化背景
数学核心素养与高考备考
考什么?
怎么考?
怎么办?
---
交流与提升
---
同课章节目录
