高考数学解题思路:立几利器——立体几何非主流好题赏析(Word版含解析)
文档属性
| 名称 | 高考数学解题思路:立几利器——立体几何非主流好题赏析(Word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-19 09:13:56 | ||
图片预览




文档简介
立体几何利器——立体几何非常规题型鉴赏
1.图1中的机械设备叫做“转子发动机”,其核心零部件之一的转子形状是“曲侧面三棱柱”,图2是一个曲侧面三棱柱,它的侧棱垂直于底面,底面是“莱洛三角形”,莱洛三角形是以正三角形的三个顶点为圆心,正三角形的边长为半径画圆弧得到的,如图3.若曲侧面三棱柱的高为10,底面任意两顶点之间的距离为20,则其侧面积为( )
A.false B.600 C.false D.false
【答案】C
【析解】
莱洛三角形由三段半径为20,圆心角为false的圆弧构成,所以该零件底面周长为false,故其侧面积为false.
故选:C.
2.空间直角坐标系false中,经过点false,且法向量为false的平面方程为false,经过点false且一个方向向量为false的直线false的方程为false,阅读上面的材料并解决下面问题:现给出平面false的方程为false,经过false的直线false的方程为false,则直线false与平面false所成角的正弦值为( )
A.false B.false C.false D.false
【答案】B
【析解】
因为平面false的方程为false,故其法向量为false,
因为直线false的方程为false,故其方向向量为false,
故直线false与平面false所成角的正弦值为false,
故选:B.
3.我国南北朝时期的著名数学家祖暅原提出了祖暅原理:“幂势既同,则积不容异.”意思是,夹在两个平行平面之间的两个几何体,被平行于这两个平面的任意一个平面所截,若截面面积都相等,则这两个几何体的体积相等.运用祖暅原理计算球的体积时,构造一个底面半径和高都与球的半径相等的圆柱,与半球(如图①)放置在同一平面上,然后在圆柱内挖去一个以圆柱下底面圆心为顶点,圆柱上底面为底面的圆锥后得到一新几何体(如图②),用任何一个平行于底面的平面去截它们时,可证得所截得的两个截面面积相等,由此可证明新几何体与半球体积相等,即false.现将椭圆false绕false轴旋转一周后得一橄榄状的几何体(如图③),类比上述方法,运用祖暅原理可求得其体积等于( )
A.false B.false C.false D.false
【答案】D
【详解】
构造一个底面半径为false,高为false的圆柱,
在圆柱中挖去一个以圆柱下底面圆心为顶点的圆锥,
则当截面与顶点距离为false时,小圆锥底面半径为false,则false,
false,故截面面积为:false,把false代入false,
即false,解得:false,false橄榄球形几何体的截面面积为false,由祖暅原理可得橄榄球形几何体的体积为:
false圆柱false圆锥false.故选:D.
371157510058404.将地球近似看作球体.设地球表面某地正午太阳高度角为false,false为此时太阳直射纬度(当地夏半年取正值,冬半年取负值),false为该地的纬度值,如图.已知太阳每年直射范围在南北回归线之间,即false.北京天安门广场的汉白玉华表高为9.57米,北京天安门广场的纬度为北纬false,若某天的正午时刻,测得华表的影长恰好为9.57米,则该天的太阳直射纬度为( )
A.北纬false B.南纬false
C.北纬false D.南纬false
【答案】D
【详解】
由题可知,天安门广场的太阳高度角false,
由华表的高和影长相等可知false,所以false.
所以该天太阳直射纬度为南纬false,
故选:D.
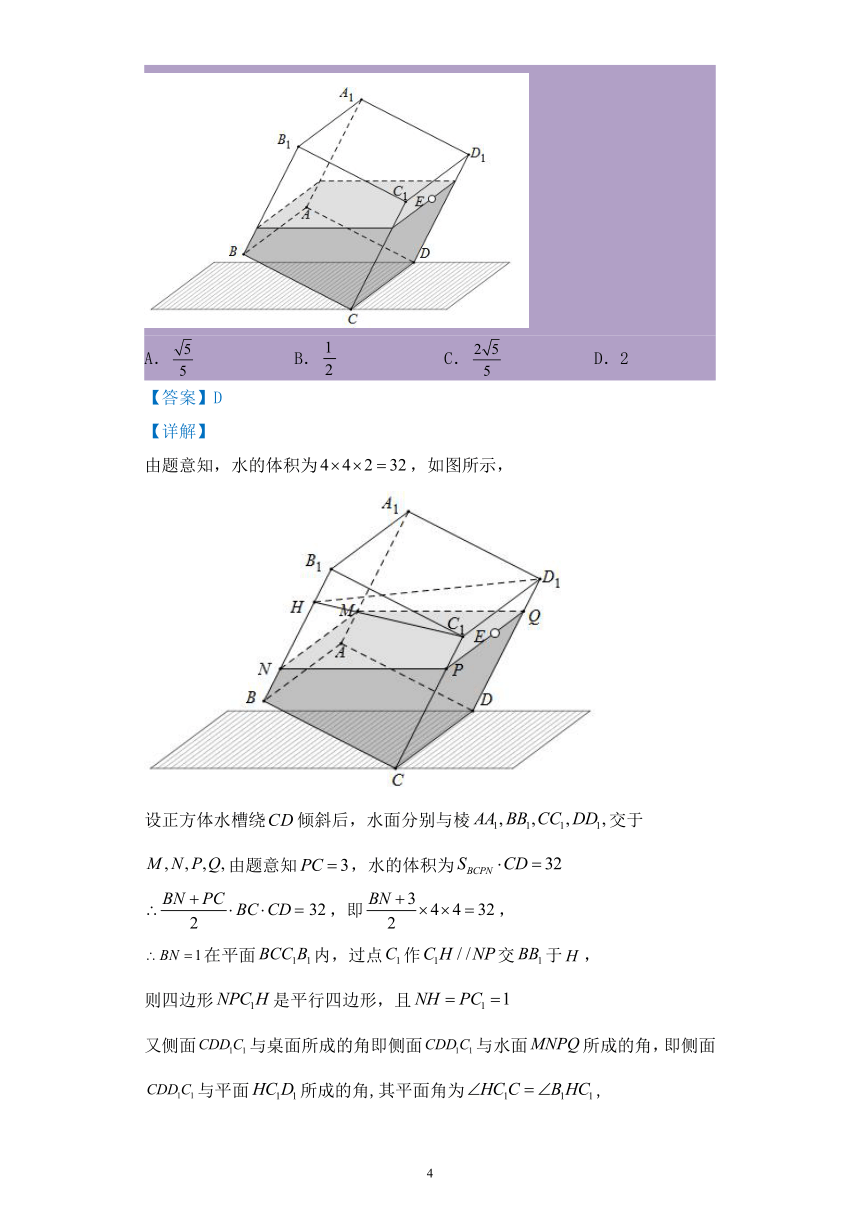
5.如图,水平桌面上放置一个棱长为4的正方体水槽,水面高度恰为正方体棱长的一半,在该正方体侧面false上有一个小孔false,false点到false的距离为3,若该正方体水槽绕false倾斜(false始终在桌面上),则当水恰好流出时,侧面false与桌面所成角的正切值为( )
A.false B.false C.false D.2
【答案】D
【详解】
由题意知,水的体积为false,如图所示,
设正方体水槽绕false倾斜后,水面分别与棱false交于false由题意知false,水的体积为false
false,即false,
false在平面false内,过点false作false交false于false,
则四边形false是平行四边形,且false
又侧面false与桌面所成的角即侧面false与水面false所成的角,即侧面false与平面false所成的角,其平面角为false,
在直角三角形false中,false.
故选:D.
6.空间中13个不同的点构成的集合false,满足当false时,false都是正四面体.对于任意平面false,false的最大值是( )
A.9 B.10 C.11 D.12
【答案】C
【详解】
为使得对于任意平面false,false取得最大值,
故要使得使之在同一平面中三棱锥顶点最多,
如下所示:
如图所示:三棱锥false,均为正四面体,显然,最多有11个点在同一平面中.
同时,若同一平面中存在12个三棱锥的顶点,则只有1个点在平面外,
无法构造几何体.故false的最大值为:false.故选:false.
7.设false、false、…、false为平面false内的false个点,在平面false内的所有点中,若点false到false、false、…、false点的距离之和最小,则称点false为false、false、…、false点的一个“中位点”,有下列命题:①false、false、false三个点共线,false在线段false上,则false是false、false、false的中位点;②直角三角形斜边的中点是该直线三角形三个顶点的中位点;③若四个点false、false、false、false共线,则它们的中位点存在且唯一;④梯形对角线的交点是该梯形四个顶点的唯一中位点;其中的真命题是( )
A.②④ B.①② C.①④ D.①③④
【答案】C
【详解】
①若三个点false共线,false在线段false上,根据两点之间线段最短,
则false是false的中位点,正确;
②举一个反例,如边长为false的直角三角形false,此直角三角形的斜边的中点到三个顶点的距离之和为false,而直角顶点到三个顶点的距离之和为7,∴直角三角形斜边的中点不是该直角三角形三个顶点的中位点;故错误;
③若四个点false共线,则它们的中位点是中间两点连线段上的任意一个点,故它们的中位点存在但不唯一;故错误;
④如图,在梯形false中,对角线的交点falsefalse是任意一点,则根据三角形两边之和大于第三边得false,
∴梯形对角线的交点是该梯形四个顶点的唯一中位点.正确.
故①④正确.故选:C
8.若点false为点false在平面false上的正投影,则记false.如图,在棱长为false的正方体false中,记平面false为false,平面false为false,点false是棱false上一动点(与false、false不重合)false,false.给出下列三个结论:
①线段false长度的取值范围是false;②存在点false使得false平面false;
③存在点false使得false.其中,所有正确结论的序号是
A.①②③ B.②③ C.①③ D.①②
【答案】D
【详解】
取false的中点false,过点false在平面false内作false,再过点false在平面false内作false,垂足为点false.
在正方体false中,false平面false,false平面false,false,又false,false,false平面false,即false,false,同理可证false,false,则false,false.以点false为坐标原点,false、false、false所在直线分别为false轴、false轴、false轴建立空间直角坐标系false,设false,则false,false,false,false,false.
对于命题①,false,false,则false,则false,所以,false,命题①正确;
对于命题②,false,则平面false的一个法向量为false,
false,令false,解得false,
所以,存在点false使得false平面false,命题②正确;
对于命题③,false,令false,
整理得false,该方程无解,所以,不存在点false使得false,命题③错误.
故选:D.
9.如图,设false为正四面体false表面(含棱)上与顶点不重合的一点,由点false到四个顶点的距离组成的集合记为false,如果集合false中有且只有false个元素,那么符合条件的点false有.
A.false个 B.false个 C.false个 D.false个
【答案】C
【详解】
试题分析:分以下两种情况讨论:(1)点false到其中两个点的距离相等,到另外两点的距离分别相等,且这两个距离不等,此时点false位于正四面体各棱的中点,符合条件的有false个点;
点false到其中三个点的距离相等,到另外一点的距离与它到其它三点的距离不相等,此时点false在正四面体各侧面的中心点,符合条件的有false个点,故选C.
10.在三维空间中,定义向量的外积:false叫做向量false与false的外积,它是一个向量,满足下列两个条件:①false,false,且false,false和false构成右手系(即三个向量的方向依次与右手的拇指、食指、中指的指向一致,如图所示):②false的模false(false表示向量false,false的夹角)在正方体false中,有以下四个结论,正确的有( )
A.false B.false
C.false方向相同 D.false与正方体表面积的数值相等
【答案】ACD
【详解】
设正方体的棱长为false,
对于A,如图,因为false为等边三角形,故false,
因为false,而false为等边三角形,
故false,故A正确.
对于B,根据定义,false,false,两者不相等,故B错.
对于C,因为false平面false,结合外积的定义可得false的方向即为false的方向,
故C正确.
对于D,false,故它与正方体的表面积相同,
故选:ACD.
11.平面中两条直线l和n相交于O,对于平面上任意一点M,若p,q分别是M到直线l和n的距离,则称有序非负实数对(p,q)是点M的“距离坐标”.则下列说法正确的( )
A.若p=q=0,则“距离坐标”为(0,0)的点有且仅有一个
B.若pq=0,且p+q≠0,则“距离坐标”为(p,q)的点有且仅有2个
C.若pq≠0,则“距离坐标”为(p,q)的点有且仅有4个
D.若p=q,则点M的轨迹是一条过O点的直线
【答案】ABC
【详解】
首先点到直线的距离是唯一确定的.
对于A选项,由于false,所以false表示false点,有且仅有一个,故A选项正确.对于B选项,由于false,且false,当false或false时,分别表示点false或false,有且仅有两个,故B选项正确.
对于C选项,由于false和false相交与false,所以直线false和直线false确定一个平面false,根据对称性可知,在平面false的上方和下方,各有两个“距离坐标”为false的点.故“距离坐标”为false的点有且仅有false个,所以C选项正确.
对于D选项,设false和false相交与false,直线false和直线false相交所形成的两组对角的角平分线上的点,都满足false,所以点false的轨迹不只是一条过false点的直线,所以D选项错误.由于false,故选:ABC
12.古希腊数学家阿波罗尼斯发现:平面上到两定点false、false距离之比false是常数的点的轨迹是一个圆心在直线false上的圆,该圆简称为阿氏圆.根据以上信息,解决下面的问题:在棱长为2的正方体false中,点false是正方体的表面false(包括边界)上的动点,若动点false满足false,则点false所形成的阿氏圆的半径为______;若false是false的中点,且满足false,则三棱锥false体积的最大值是______.
阿波罗尼奥斯
【答案】false false
【详解】
在false上取点false,在false延长线上取点false,使得false,false,则false是题中阿氏圆上的点,由题意false是阿氏圆的直径,
false,则false,false,所以false,∴阿氏圆半径为false;
正方体中false,false都与侧面false垂直,从而与侧面false内的直线false垂直,如图false,则false,∴false,即false在上述阿氏圆上,∵false的面积是2为定值,因此只要false到平面false距离最大,则三棱锥false体积的最大,由于false点在阿氏圆上,当false是阿氏圆与false交点false时,false到平面false距离最大,此时false,因此false,false,三棱锥false体积的最大值为false.
故答案为:false;false.
13.古希腊数学家阿波罗尼奥斯发现:平面上到两定点false,false距离之比为常数false且false的点的轨迹是一个圆心在直线false上的圆,该圆简称为阿氏圆.根据以上信息,解决下面的问题:如图,在长方体false中,false,点false在棱false上,false,动点false满足false.若点false在平面false内运动,则点false所形成的阿氏圆的半径为________;若点false在长方体false内部运动,false为棱false的中点,false为false的中点,则三棱锥false的体积的最小值为___________.
【答案】false false
【详解】
(1)以AB为false轴,AD为false轴,false为false轴,建立如图所示的坐标系,则false设false,由false得false,
所以false,所以若点false在平面false内运动,则点false所形成的阿氏圆的半径为false.
(2)设点false,由false得false,
所以false,由题得false
所以false设平面false的法向量为false,
所以false,
由题得false,
所以点P到平面false的距离为false,
因为false,
所以false,所以点M到平面false的最小距离为false,
由题得false为等边三角形,且边长为false,
所以三棱锥false的体积的最小值为false.
故答案为:(1). false (2). false .
14.北京大兴国际机场的显著特点之一是各种弯曲空间的运用.刻画空间的弯曲性是几何研究的重要内容.用曲率刻画空间弯曲性,规定:多面体顶点的曲率等于false与多面体在该点的面角之和的差(多面体的面的内角叫做多面体的面角,角度用弧度制),多面体面上非顶点的曲率均为零,多面体的总曲率等于该多面体各顶点的曲率之和.例如:正四面体在每个顶点有3个面角,每个面角是false,所以正四面体在各顶点的曲率为false,故其总曲率为false.
(1)求四棱锥的总曲率;
(2)若多面体满足:顶点数-棱数+面数false,证明:这类多面体的总曲率是常数.
【答案】(1)false;(2)证明见解析.
【详解】
(1)由题可知:四棱锥的总曲率等于四棱锥各顶点的曲率之和.
可以从整个多面体的角度考虑,所有顶点相关的面角就是多面体的所有多边形表面的内角的集合.由图可知:四棱锥共有5个顶点,5个面,其中4个为三角形,1个为四边形.所以四棱锥的表面内角和由4个为三角形,1个为四边形组成,则其总曲率为:false.
(2)设顶点数、棱数、面数分别为false、false、false,所以有false
设第false个面的棱数为false,所以false
所以总曲率为:false
falsefalse所以这类多面体的总曲率是常数.
15.已知集合false,定义false上两点false,
false的距离false.
(1)当false时,以下命题正确的有__________(不需证明):
①若false,false,则false;
②在false中,若false,则false;
③在false中,若false,则false;
(2)当false时,证明false中任意三点false满足关系false;
(3)当false时,设false,false,false,其中false,
false.求满足false点的个数false,并证明从这false个点中任取11个点,其中必存在4个点,它们共面或者以它们为顶点的三棱锥体积不大于false.
【答案】(1)①;(2)证明见解析;(3)false,证明见解析.
【详解】
(1)当false时,
①若false,false,则false,①正确;
②在false中,若false,则false,设false,所以false
而false,
falsefalse,但false不一定成立,②错误;③在false中,若false,在②中的点坐标,有false,但false不一定成立,因此false不一定成立,从而false不一定成立,③错误.
空格处填①
(2)证明:设false,根据绝对值的性质有
false,false,
所以false.,
(3)false,
false,所以false,当且仅当以上三个等号同时成立,false
又由已知false,∴false,
又false,∴false,false,
点false是以false为对角线的正方体内部(含面上)的整数点,共125个,false.
这125个点在false这五面内.
这三个平面内,一个面上取不共线的3点,相邻面上再取一点构成一个三棱锥.则这个三棱锥的体积最大为false,
现在任取11个点,若有四点共面,则命题已成立,若其中无4点共面,但11个点分在5个平面上至少有一个平面内有3个点(显然不共线),
若这三点在false这三个平面中的一个上,与这个面相邻的两个面上如果有一点,那么这一点与平面上的三点这四点可构成三棱锥的四个顶点,其体积不超过false,否则还有8个点在平面false和false上,不合题意,
若这三个点在平面false或false上,不妨设在平面false,若在平面false在一个点,则同样四点构成的三棱锥体积不超过false,否则剩下的8个点在false三个平面上,只能是3,3,2分布,不管哪一种分布都有四点构成的三棱锥体积不超过false,
综上,任取11个点,其中必存在4个点,它们共面或者以它们为顶点的三棱锥体积不大于false.
16.(1)如图,对于任一给定的四面体false,找出依次排列的四个相互平行的平面false,false,false,false,使得false,且其中每相邻两个平面间的距离都相等;
(2)给定依次排列的四个相互平行的平面false,false,false,false,其中每相邻两个平面间的距离为1,若一个正四面体false的四个顶点满足:false,求该正四面体false的体积.
【答案】(1)见解析; (2)false.
【详解】
(1)
取false的三等分点false,false,false的中点false,false的中点false,
过三点false,false,false作平面false,过三点false,false,false作平面false,
因为false,false,所以平面false平面false,
再过点false,false分别作平面false,false与平面false平行,那么四个平面,false,false,false依次相互平行,由线段false被平行平面false,false,false,false截得的线段相等知,每相邻两个平面间的距离相等,故false,false,false,false为所求平面.
(2)如图,将此正四面体补形为正方体false(如图),
分别取false、false、false、false的中点false、false、false、false,
平面false与false是分别过点false、false的两平行平面,若其距离为1,
则正四面体false满足条件,右图为正方体的下底面,设正方体的棱长为false,
若false,因为false,false,
在直角三角形false中,false,所以false,所以false,
又正四面体的棱长为false,
所以此正四面体的体积为false.
17.在空间直角坐标系中,定义:平面false的一般方程为false,点false到平面false的距离false,则在底面边长与高都为2的正四棱锥中,底面中心O到侧面的距离等于________.
【答案】false
【详解】
如图,以底面中心false为原点建立空间直角坐标系false,
则false,false,1,false,false,1,false,false,0,false,
设平面false的方程为false,
将false坐标代入计算得false解得false,false,false,
false,即false,false.
故答案为:false
18.古代中国,建筑工匠们非常注重建筑中体现数学美,方形和圆形的应用比比皆是,在唐、宋时期的单檐建筑中较多存在false的比例关系,这是当时工匠们着意设计的常见比例,今天,false纸之所以流行的重要原因之一,就是它的长与宽的比无限接近false,我们称这种满足了false的矩形为“优美”矩形.现有一长方体false,false,false,false,则此长方体的表面六个矩形中,“优美”矩形的个数为___________.
【答案】4
【详解】
由题意,该长方体如图所示:
falsefalse,false,false,
falsefalse,false,
false,falsefalse,false,
falsefalse,false,false,false此长方体的表面六个矩形中,“优美”矩形的个数为4.故答案为:4.
19.瑞士数学家、物理学家欧拉发现任一凸多面体(即多面体内任意两点的连线都被完全包含在该多面体中,直观上讲是指没有凹陷或孔洞的多面体)的顶点数false,棱数false及面数false满足等式false,这个等式称为欧拉多面体公式,被认为是数学领域最漂亮,简洁的公式之一.如图是一个面数为26的多面体(其表面仅由正方形和正三角形围成),根据欧拉多面体公式可求得其棱数false_______.
【答案】48
【详解】该多面体面数false,由图知,顶点数false,
根据欧拉多面体公式false得:棱数false.
故答案为:false.
20.如图,在直角梯形ABCD中,AB∥CD,∠ABC=90°,AB=1,AC=CD=DA=2,动点M在边DC上(不同于D点),P为边AB上任意一点,沿AM将△ADM翻折成△AD'M,当平面AD'M垂直于平面ABC时,线段PD'长度的最小值为_____.
【答案】false
【详解】
过D′作AM的垂线,垂足为H,由题意可知D′A=DA=2,随着点M在边DC上向点C方向移动,DM逐渐变大,即D'M越来越大,又D′H为三角形AD'M中AM边上的高,D′A长度不变,D'M越来越大,所以垂足为H越来越靠近点A,所以当点M与C重合即折痕为AC时,H到直线AB的距离最小,又AC=CD=DA=2,所以AC=CD′=D′A=2,此时H为AC的中点,所以D′H=DHfalse,此时,H到直线AB的最小距离为hfalseBCfalse,所以PD′的最小距离为false.
故答案为:false
1.图1中的机械设备叫做“转子发动机”,其核心零部件之一的转子形状是“曲侧面三棱柱”,图2是一个曲侧面三棱柱,它的侧棱垂直于底面,底面是“莱洛三角形”,莱洛三角形是以正三角形的三个顶点为圆心,正三角形的边长为半径画圆弧得到的,如图3.若曲侧面三棱柱的高为10,底面任意两顶点之间的距离为20,则其侧面积为( )
A.false B.600 C.false D.false
【答案】C
【析解】
莱洛三角形由三段半径为20,圆心角为false的圆弧构成,所以该零件底面周长为false,故其侧面积为false.
故选:C.
2.空间直角坐标系false中,经过点false,且法向量为false的平面方程为false,经过点false且一个方向向量为false的直线false的方程为false,阅读上面的材料并解决下面问题:现给出平面false的方程为false,经过false的直线false的方程为false,则直线false与平面false所成角的正弦值为( )
A.false B.false C.false D.false
【答案】B
【析解】
因为平面false的方程为false,故其法向量为false,
因为直线false的方程为false,故其方向向量为false,
故直线false与平面false所成角的正弦值为false,
故选:B.
3.我国南北朝时期的著名数学家祖暅原提出了祖暅原理:“幂势既同,则积不容异.”意思是,夹在两个平行平面之间的两个几何体,被平行于这两个平面的任意一个平面所截,若截面面积都相等,则这两个几何体的体积相等.运用祖暅原理计算球的体积时,构造一个底面半径和高都与球的半径相等的圆柱,与半球(如图①)放置在同一平面上,然后在圆柱内挖去一个以圆柱下底面圆心为顶点,圆柱上底面为底面的圆锥后得到一新几何体(如图②),用任何一个平行于底面的平面去截它们时,可证得所截得的两个截面面积相等,由此可证明新几何体与半球体积相等,即false.现将椭圆false绕false轴旋转一周后得一橄榄状的几何体(如图③),类比上述方法,运用祖暅原理可求得其体积等于( )
A.false B.false C.false D.false
【答案】D
【详解】
构造一个底面半径为false,高为false的圆柱,
在圆柱中挖去一个以圆柱下底面圆心为顶点的圆锥,
则当截面与顶点距离为false时,小圆锥底面半径为false,则false,
false,故截面面积为:false,把false代入false,
即false,解得:false,false橄榄球形几何体的截面面积为false,由祖暅原理可得橄榄球形几何体的体积为:
false圆柱false圆锥false.故选:D.
371157510058404.将地球近似看作球体.设地球表面某地正午太阳高度角为false,false为此时太阳直射纬度(当地夏半年取正值,冬半年取负值),false为该地的纬度值,如图.已知太阳每年直射范围在南北回归线之间,即false.北京天安门广场的汉白玉华表高为9.57米,北京天安门广场的纬度为北纬false,若某天的正午时刻,测得华表的影长恰好为9.57米,则该天的太阳直射纬度为( )
A.北纬false B.南纬false
C.北纬false D.南纬false
【答案】D
【详解】
由题可知,天安门广场的太阳高度角false,
由华表的高和影长相等可知false,所以false.
所以该天太阳直射纬度为南纬false,
故选:D.
5.如图,水平桌面上放置一个棱长为4的正方体水槽,水面高度恰为正方体棱长的一半,在该正方体侧面false上有一个小孔false,false点到false的距离为3,若该正方体水槽绕false倾斜(false始终在桌面上),则当水恰好流出时,侧面false与桌面所成角的正切值为( )
A.false B.false C.false D.2
【答案】D
【详解】
由题意知,水的体积为false,如图所示,
设正方体水槽绕false倾斜后,水面分别与棱false交于false由题意知false,水的体积为false
false,即false,
false在平面false内,过点false作false交false于false,
则四边形false是平行四边形,且false
又侧面false与桌面所成的角即侧面false与水面false所成的角,即侧面false与平面false所成的角,其平面角为false,
在直角三角形false中,false.
故选:D.
6.空间中13个不同的点构成的集合false,满足当false时,false都是正四面体.对于任意平面false,false的最大值是( )
A.9 B.10 C.11 D.12
【答案】C
【详解】
为使得对于任意平面false,false取得最大值,
故要使得使之在同一平面中三棱锥顶点最多,
如下所示:
如图所示:三棱锥false,均为正四面体,显然,最多有11个点在同一平面中.
同时,若同一平面中存在12个三棱锥的顶点,则只有1个点在平面外,
无法构造几何体.故false的最大值为:false.故选:false.
7.设false、false、…、false为平面false内的false个点,在平面false内的所有点中,若点false到false、false、…、false点的距离之和最小,则称点false为false、false、…、false点的一个“中位点”,有下列命题:①false、false、false三个点共线,false在线段false上,则false是false、false、false的中位点;②直角三角形斜边的中点是该直线三角形三个顶点的中位点;③若四个点false、false、false、false共线,则它们的中位点存在且唯一;④梯形对角线的交点是该梯形四个顶点的唯一中位点;其中的真命题是( )
A.②④ B.①② C.①④ D.①③④
【答案】C
【详解】
①若三个点false共线,false在线段false上,根据两点之间线段最短,
则false是false的中位点,正确;
②举一个反例,如边长为false的直角三角形false,此直角三角形的斜边的中点到三个顶点的距离之和为false,而直角顶点到三个顶点的距离之和为7,∴直角三角形斜边的中点不是该直角三角形三个顶点的中位点;故错误;
③若四个点false共线,则它们的中位点是中间两点连线段上的任意一个点,故它们的中位点存在但不唯一;故错误;
④如图,在梯形false中,对角线的交点falsefalse是任意一点,则根据三角形两边之和大于第三边得false,
∴梯形对角线的交点是该梯形四个顶点的唯一中位点.正确.
故①④正确.故选:C
8.若点false为点false在平面false上的正投影,则记false.如图,在棱长为false的正方体false中,记平面false为false,平面false为false,点false是棱false上一动点(与false、false不重合)false,false.给出下列三个结论:
①线段false长度的取值范围是false;②存在点false使得false平面false;
③存在点false使得false.其中,所有正确结论的序号是
A.①②③ B.②③ C.①③ D.①②
【答案】D
【详解】
取false的中点false,过点false在平面false内作false,再过点false在平面false内作false,垂足为点false.
在正方体false中,false平面false,false平面false,false,又false,false,false平面false,即false,false,同理可证false,false,则false,false.以点false为坐标原点,false、false、false所在直线分别为false轴、false轴、false轴建立空间直角坐标系false,设false,则false,false,false,false,false.
对于命题①,false,false,则false,则false,所以,false,命题①正确;
对于命题②,false,则平面false的一个法向量为false,
false,令false,解得false,
所以,存在点false使得false平面false,命题②正确;
对于命题③,false,令false,
整理得false,该方程无解,所以,不存在点false使得false,命题③错误.
故选:D.
9.如图,设false为正四面体false表面(含棱)上与顶点不重合的一点,由点false到四个顶点的距离组成的集合记为false,如果集合false中有且只有false个元素,那么符合条件的点false有.
A.false个 B.false个 C.false个 D.false个
【答案】C
【详解】
试题分析:分以下两种情况讨论:(1)点false到其中两个点的距离相等,到另外两点的距离分别相等,且这两个距离不等,此时点false位于正四面体各棱的中点,符合条件的有false个点;
点false到其中三个点的距离相等,到另外一点的距离与它到其它三点的距离不相等,此时点false在正四面体各侧面的中心点,符合条件的有false个点,故选C.
10.在三维空间中,定义向量的外积:false叫做向量false与false的外积,它是一个向量,满足下列两个条件:①false,false,且false,false和false构成右手系(即三个向量的方向依次与右手的拇指、食指、中指的指向一致,如图所示):②false的模false(false表示向量false,false的夹角)在正方体false中,有以下四个结论,正确的有( )
A.false B.false
C.false方向相同 D.false与正方体表面积的数值相等
【答案】ACD
【详解】
设正方体的棱长为false,
对于A,如图,因为false为等边三角形,故false,
因为false,而false为等边三角形,
故false,故A正确.
对于B,根据定义,false,false,两者不相等,故B错.
对于C,因为false平面false,结合外积的定义可得false的方向即为false的方向,
故C正确.
对于D,false,故它与正方体的表面积相同,
故选:ACD.
11.平面中两条直线l和n相交于O,对于平面上任意一点M,若p,q分别是M到直线l和n的距离,则称有序非负实数对(p,q)是点M的“距离坐标”.则下列说法正确的( )
A.若p=q=0,则“距离坐标”为(0,0)的点有且仅有一个
B.若pq=0,且p+q≠0,则“距离坐标”为(p,q)的点有且仅有2个
C.若pq≠0,则“距离坐标”为(p,q)的点有且仅有4个
D.若p=q,则点M的轨迹是一条过O点的直线
【答案】ABC
【详解】
首先点到直线的距离是唯一确定的.
对于A选项,由于false,所以false表示false点,有且仅有一个,故A选项正确.对于B选项,由于false,且false,当false或false时,分别表示点false或false,有且仅有两个,故B选项正确.
对于C选项,由于false和false相交与false,所以直线false和直线false确定一个平面false,根据对称性可知,在平面false的上方和下方,各有两个“距离坐标”为false的点.故“距离坐标”为false的点有且仅有false个,所以C选项正确.
对于D选项,设false和false相交与false,直线false和直线false相交所形成的两组对角的角平分线上的点,都满足false,所以点false的轨迹不只是一条过false点的直线,所以D选项错误.由于false,故选:ABC
12.古希腊数学家阿波罗尼斯发现:平面上到两定点false、false距离之比false是常数的点的轨迹是一个圆心在直线false上的圆,该圆简称为阿氏圆.根据以上信息,解决下面的问题:在棱长为2的正方体false中,点false是正方体的表面false(包括边界)上的动点,若动点false满足false,则点false所形成的阿氏圆的半径为______;若false是false的中点,且满足false,则三棱锥false体积的最大值是______.
阿波罗尼奥斯
【答案】false false
【详解】
在false上取点false,在false延长线上取点false,使得false,false,则false是题中阿氏圆上的点,由题意false是阿氏圆的直径,
false,则false,false,所以false,∴阿氏圆半径为false;
正方体中false,false都与侧面false垂直,从而与侧面false内的直线false垂直,如图false,则false,∴false,即false在上述阿氏圆上,∵false的面积是2为定值,因此只要false到平面false距离最大,则三棱锥false体积的最大,由于false点在阿氏圆上,当false是阿氏圆与false交点false时,false到平面false距离最大,此时false,因此false,false,三棱锥false体积的最大值为false.
故答案为:false;false.
13.古希腊数学家阿波罗尼奥斯发现:平面上到两定点false,false距离之比为常数false且false的点的轨迹是一个圆心在直线false上的圆,该圆简称为阿氏圆.根据以上信息,解决下面的问题:如图,在长方体false中,false,点false在棱false上,false,动点false满足false.若点false在平面false内运动,则点false所形成的阿氏圆的半径为________;若点false在长方体false内部运动,false为棱false的中点,false为false的中点,则三棱锥false的体积的最小值为___________.
【答案】false false
【详解】
(1)以AB为false轴,AD为false轴,false为false轴,建立如图所示的坐标系,则false设false,由false得false,
所以false,所以若点false在平面false内运动,则点false所形成的阿氏圆的半径为false.
(2)设点false,由false得false,
所以false,由题得false
所以false设平面false的法向量为false,
所以false,
由题得false,
所以点P到平面false的距离为false,
因为false,
所以false,所以点M到平面false的最小距离为false,
由题得false为等边三角形,且边长为false,
所以三棱锥false的体积的最小值为false.
故答案为:(1). false (2). false .
14.北京大兴国际机场的显著特点之一是各种弯曲空间的运用.刻画空间的弯曲性是几何研究的重要内容.用曲率刻画空间弯曲性,规定:多面体顶点的曲率等于false与多面体在该点的面角之和的差(多面体的面的内角叫做多面体的面角,角度用弧度制),多面体面上非顶点的曲率均为零,多面体的总曲率等于该多面体各顶点的曲率之和.例如:正四面体在每个顶点有3个面角,每个面角是false,所以正四面体在各顶点的曲率为false,故其总曲率为false.
(1)求四棱锥的总曲率;
(2)若多面体满足:顶点数-棱数+面数false,证明:这类多面体的总曲率是常数.
【答案】(1)false;(2)证明见解析.
【详解】
(1)由题可知:四棱锥的总曲率等于四棱锥各顶点的曲率之和.
可以从整个多面体的角度考虑,所有顶点相关的面角就是多面体的所有多边形表面的内角的集合.由图可知:四棱锥共有5个顶点,5个面,其中4个为三角形,1个为四边形.所以四棱锥的表面内角和由4个为三角形,1个为四边形组成,则其总曲率为:false.
(2)设顶点数、棱数、面数分别为false、false、false,所以有false
设第false个面的棱数为false,所以false
所以总曲率为:false
falsefalse所以这类多面体的总曲率是常数.
15.已知集合false,定义false上两点false,
false的距离false.
(1)当false时,以下命题正确的有__________(不需证明):
①若false,false,则false;
②在false中,若false,则false;
③在false中,若false,则false;
(2)当false时,证明false中任意三点false满足关系false;
(3)当false时,设false,false,false,其中false,
false.求满足false点的个数false,并证明从这false个点中任取11个点,其中必存在4个点,它们共面或者以它们为顶点的三棱锥体积不大于false.
【答案】(1)①;(2)证明见解析;(3)false,证明见解析.
【详解】
(1)当false时,
①若false,false,则false,①正确;
②在false中,若false,则false,设false,所以false
而false,
falsefalse,但false不一定成立,②错误;③在false中,若false,在②中的点坐标,有false,但false不一定成立,因此false不一定成立,从而false不一定成立,③错误.
空格处填①
(2)证明:设false,根据绝对值的性质有
false,false,
所以false.,
(3)false,
false,所以false,当且仅当以上三个等号同时成立,false
又由已知false,∴false,
又false,∴false,false,
点false是以false为对角线的正方体内部(含面上)的整数点,共125个,false.
这125个点在false这五面内.
这三个平面内,一个面上取不共线的3点,相邻面上再取一点构成一个三棱锥.则这个三棱锥的体积最大为false,
现在任取11个点,若有四点共面,则命题已成立,若其中无4点共面,但11个点分在5个平面上至少有一个平面内有3个点(显然不共线),
若这三点在false这三个平面中的一个上,与这个面相邻的两个面上如果有一点,那么这一点与平面上的三点这四点可构成三棱锥的四个顶点,其体积不超过false,否则还有8个点在平面false和false上,不合题意,
若这三个点在平面false或false上,不妨设在平面false,若在平面false在一个点,则同样四点构成的三棱锥体积不超过false,否则剩下的8个点在false三个平面上,只能是3,3,2分布,不管哪一种分布都有四点构成的三棱锥体积不超过false,
综上,任取11个点,其中必存在4个点,它们共面或者以它们为顶点的三棱锥体积不大于false.
16.(1)如图,对于任一给定的四面体false,找出依次排列的四个相互平行的平面false,false,false,false,使得false,且其中每相邻两个平面间的距离都相等;
(2)给定依次排列的四个相互平行的平面false,false,false,false,其中每相邻两个平面间的距离为1,若一个正四面体false的四个顶点满足:false,求该正四面体false的体积.
【答案】(1)见解析; (2)false.
【详解】
(1)
取false的三等分点false,false,false的中点false,false的中点false,
过三点false,false,false作平面false,过三点false,false,false作平面false,
因为false,false,所以平面false平面false,
再过点false,false分别作平面false,false与平面false平行,那么四个平面,false,false,false依次相互平行,由线段false被平行平面false,false,false,false截得的线段相等知,每相邻两个平面间的距离相等,故false,false,false,false为所求平面.
(2)如图,将此正四面体补形为正方体false(如图),
分别取false、false、false、false的中点false、false、false、false,
平面false与false是分别过点false、false的两平行平面,若其距离为1,
则正四面体false满足条件,右图为正方体的下底面,设正方体的棱长为false,
若false,因为false,false,
在直角三角形false中,false,所以false,所以false,
又正四面体的棱长为false,
所以此正四面体的体积为false.
17.在空间直角坐标系中,定义:平面false的一般方程为false,点false到平面false的距离false,则在底面边长与高都为2的正四棱锥中,底面中心O到侧面的距离等于________.
【答案】false
【详解】
如图,以底面中心false为原点建立空间直角坐标系false,
则false,false,1,false,false,1,false,false,0,false,
设平面false的方程为false,
将false坐标代入计算得false解得false,false,false,
false,即false,false.
故答案为:false
18.古代中国,建筑工匠们非常注重建筑中体现数学美,方形和圆形的应用比比皆是,在唐、宋时期的单檐建筑中较多存在false的比例关系,这是当时工匠们着意设计的常见比例,今天,false纸之所以流行的重要原因之一,就是它的长与宽的比无限接近false,我们称这种满足了false的矩形为“优美”矩形.现有一长方体false,false,false,false,则此长方体的表面六个矩形中,“优美”矩形的个数为___________.
【答案】4
【详解】
由题意,该长方体如图所示:
falsefalse,false,false,
falsefalse,false,
false,falsefalse,false,
falsefalse,false,false,false此长方体的表面六个矩形中,“优美”矩形的个数为4.故答案为:4.
19.瑞士数学家、物理学家欧拉发现任一凸多面体(即多面体内任意两点的连线都被完全包含在该多面体中,直观上讲是指没有凹陷或孔洞的多面体)的顶点数false,棱数false及面数false满足等式false,这个等式称为欧拉多面体公式,被认为是数学领域最漂亮,简洁的公式之一.如图是一个面数为26的多面体(其表面仅由正方形和正三角形围成),根据欧拉多面体公式可求得其棱数false_______.
【答案】48
【详解】该多面体面数false,由图知,顶点数false,
根据欧拉多面体公式false得:棱数false.
故答案为:false.
20.如图,在直角梯形ABCD中,AB∥CD,∠ABC=90°,AB=1,AC=CD=DA=2,动点M在边DC上(不同于D点),P为边AB上任意一点,沿AM将△ADM翻折成△AD'M,当平面AD'M垂直于平面ABC时,线段PD'长度的最小值为_____.
【答案】false
【详解】
过D′作AM的垂线,垂足为H,由题意可知D′A=DA=2,随着点M在边DC上向点C方向移动,DM逐渐变大,即D'M越来越大,又D′H为三角形AD'M中AM边上的高,D′A长度不变,D'M越来越大,所以垂足为H越来越靠近点A,所以当点M与C重合即折痕为AC时,H到直线AB的距离最小,又AC=CD=DA=2,所以AC=CD′=D′A=2,此时H为AC的中点,所以D′H=DHfalse,此时,H到直线AB的最小距离为hfalseBCfalse,所以PD′的最小距离为false.
故答案为:false
同课章节目录
