高考数学解题思路:立几利器——立体几何综合讲义(Word版含解析)
文档属性
| 名称 | 高考数学解题思路:立几利器——立体几何综合讲义(Word版含解析) |  | |
| 格式 | |||
| 文件大小 | 7.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-19 09:15:43 | ||
图片预览



文档简介
1.1 立体几何之外接球 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
1.2 共面问题 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
1.3 平行问题 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
1.3.1 平行之点共面 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16
1.3.2 平行问题基础理论 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
1.3.3 正向平移证平行问题 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
1.3.4 平行的传递性 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
1.3.5 反向沿线找点找线平移法 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
1.4 垂直问题 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24
1.4.1 垂直问题基础理论 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24
1.4.2 垂直问题基础理论 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
1.4.3 系统法 1:面 ⊥ 面 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26
1.4.4 系统法 2:二线 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28
1.4.5 系统法 3:三勾股 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30
1.4.6 系统法 4:四图一柱 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33
1.4.7 系统法 5:五射影 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 38
1.4.8 系统法 6:转化 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39
1.4.9 平行垂直综合 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40
1.5 立体几何与空间向量 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 49
1.5.1 空间向量与线线角 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 50
1.5.2 空间向量与点到面的距离 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 51
1.5.3 定义法与角度问题 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 52
1.5.4 空间向量与线面角 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 54
1.5.5 空间向量与二面角 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 65
1.5.6 空间向量与动点设点 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 79
1.6 文科专项 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 82
1.6.1 直接法求体积 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 82
1.6.2 平行换点求体积 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 84
1.6.3 等分点求体积 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 86
1.6.4 割补法求体积 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 88
1.6.5 表面积和面积问题 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 90
1.6.6 直接法求点到面的距离 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 93
1.6.7 平行换点求点到面的距离 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 96
1.6.8 等体积法求点到面的距离 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 97
第 1 页 共 99 页
第 1 章 立体几何之外接球
1.1 立体几何之外接球
总结:? ?
球心在过两个不平行平面的外接圆圆心
球心
且分别垂直于两个平面的两条直线的交点
长方体模型
柱体模型 正方体模型
三条棱 a、 b 、 c 两两相互垂直
?
对棱相等模型 1
柱切锥(柱体的切割体)模型
核
对棱相等模型 2
心
正棱锥模型
模
锥体模型 侧棱垂直底面模型
四个模型
型
球心的投影在面的外接圆圆心上模型
?
θ =90
全等三角形折叠模型
等腰三角形底边与直角
面 α 面 β 夹角 θ 模型
三角形斜边构成二面角
的四面体
θ 为任意角
外接球之柱体模型
柱体模型:?
、 、 长方体的长宽高
a b c
√
长方体模型 2 2 2
a + b + c
R =
2
a 正方体的棱 √
柱体模型 正方体模型
2 2 2
a + a + a
R =
2
、 、 相互垂直的三条边
a b c
√
a、 b 、 c 相互垂直的三条边 a2 + b 2 + c 2
R = 2
例 1(柱体模型 )
√
a2 + b 2 + c 2
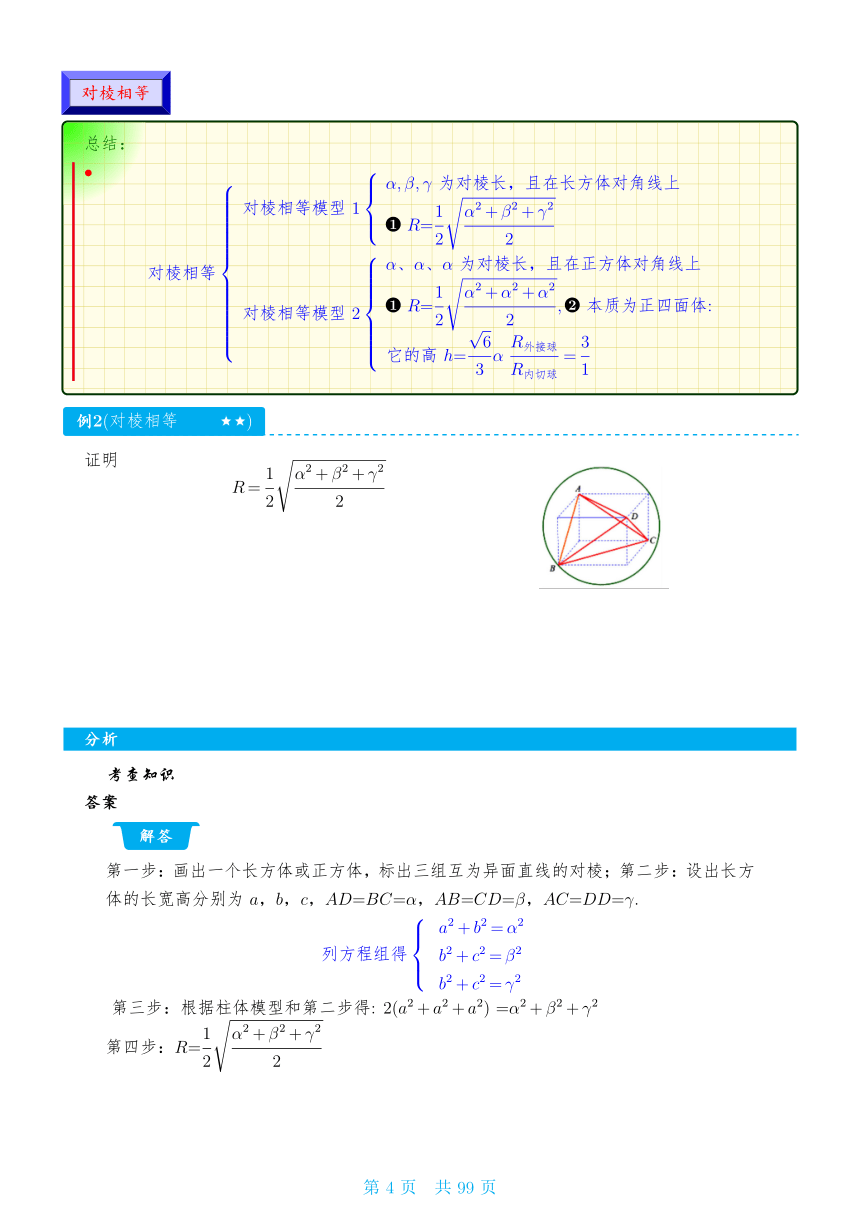
证明 R = ;
2
分析
考查知识
答案
解答 √
a2 + b 2 + c 2
由此模型可知球心在体对角线的中点,所以 R = 2
第 3 页 共 99 页
对棱相等
总结:?
α, β, γ 为对棱长,且在长方体对角线上
对棱相等模型 1 2 2 2
1 α + β + γ
R =
2 2
α 、 α 、 α 为对棱长,且在正方体对角线上
对棱相等
2 2 2
1 α + α + α
本质为正四面体
对棱相等模型 R = , :
2
2 2
√
6 R 外接球 3
它的高 h = α ? =
3 R 内切球 1
例 2(对棱相等 )
证明
2 2 2
1 α + β + γ
R =
2 2
分析
考查知识
答案
解答
第一步:画出一个长方体或正方体,标出三组互为异面直线的对棱;第二步:设出长方
体的长宽高分别为 a, b , c , AD=BC =α , AB =CD =β , AC =DD=γ .
2 2 2
a + b = α
列方程组得 2 2 2
b + c = β
2 2 2
b + c = γ
2 2 2 2 2 2
第三步:根据柱体模型和第二步得 : 2(a + a + a ) =α + β + γ
2 2 2
1 α + β + γ
第四步: R =
2 2
第 4 页 共 99 页
外接球之锥体模型
总结:?
为侧棱、 为高
b h
2
正棱锥模型 b
R =
2 h
h 侧棱长, r 为底面多边形的外接圆半径
直棱柱与直圆柱也满足此公式
锥体模型 侧棱垂直底面模型
2
h
2
R = + r
4
h 为球心到平面的距离
球心的投影在面的外接圆圆心上模型
r 为面的外接圆半径
√
R = h 2 + r 2
锥体之正棱锥模型:?
b 为侧棱、 h 为高
锥体之正棱锥模型 2
b
R =
2 h
例 3(正棱锥模型 )
2
b
证明 R =
2 h
分析
考查知识
第 5 页 共 99 页
答案
解答 由题意可知:在正棱锥 A? BCD 中, O 为球心, OA , O , OC , OD 为半径;
令 O 1 为 △ BCD 的外接圆圆心,令其半径 O 1 D 为 r ,令正棱锥的高 AO 1 为 h 令侧棱长
AD=b ;
在直角 △ DOO 1 中
2 2 2 2 2 2 2 2 2 2 2
OD = R = | OO 1 | + | DO 1 | = ( h ? R ) + r = h + r ? 2 Rh + R = b ? 2 Rh + R
2
所以 R =2 Rh , 即 2
b
R =
2 h
第 6 页 共 99 页
侧棱垂直底面或直棱柱与直圆柱模型
总结:?
h 侧棱长, r 为底面多边形的外接圆半径
直棱柱与直圆柱也满足此公式
侧棱垂直底面模型
2
h
R = + r 2
4
例 4(侧棱垂直底面模型 )
分析
考查知识
答案
解答
如第一个图,(其他证明类似) OD =R , O 1 D 为 △ ABC 的外接圆半径;
令 O 1 D= r 所以 a b c
2 r = = =
sinA sinB sinC
在 △ P AD 中,令 P A =l ,由中位线定理可知
P A h
OO 1 = =
2 2
在 △ OO 1 D 中,由勾股定理得 …
2
h
OO 1 = R = + r 2
4
第 7 页 共 99 页
球心的投影在面的外接圆圆心上模型
球心的投影在面的外接圆圆心上模型:?
h 为球心到平面的距离
球心的投影在面的外接圆圆心上模型 为面的外接圆半径
r
√
R = h 2 + r 2
例 5(球心的投影在面的外接圆圆心上模型 )
【球心的投影在面的外接圆圆心上模型图】
分析
考查知识
答案
解答
如第一个图, OC =R ,令 OO 1 =h , O 1 C = r 为 △ ABC 的外接圆半径,在 △ OO 1 C 中,
由勾股定理得 √
R= h 2 + r 2
通常利用勾股定理求解
2 2 2
R = | R ? | P O 1 || + | O 1 C |
第 8 页 共 99 页
外接球之平面 α 平面 β 夹角 θ 模型
总结:?
为 的外接圆半径
r 1 α
? r 2 为 β 的外接圆半径 l 为 α 与 β 交线
θ =90
2
l
2 2 ?
R = r + r
1 2
4
全等三角形或者等腰拼在一起
或者菱形折叠折叠的二面角为 θ
h 为一个面的顶点到两面交线中点的距离
全等三角形折叠
r 同一个面的外接圆半径
平
θ
2 ? 2 2
面
R = r + ( h r ) tan
2
α
等腰三角形底边与直角
平
三角形斜边构成二面角为 θ
面
h 等腰三角形底边的高
等腰与直角三角形
β
等腰三角形外接圆半径
r
夹
2
?
( h r )
2
角
R = r +
2
sin θ
θ
两个等腰三角形(不全部等)公底边
模
的二面角 等腰三角形底边
θ ?
型
剖面图一致
与直角三角形直角边共边二面角 θ
θ
2
2
R = r + ( h ? r ) 2 tan
2
l 为 α 与 β 交线
θ 为面 α 与面 β 的夹角
m 为 α 的外接圆圆心到 l 中点的距离
θ = 任意角
为 的外接圆圆心到 中点的距离
n β l
2 2 2
2 m + n ? 2 mncosθ l
R =
2 +
sin θ 4
总结:?
r 1 为 α 的外接圆半径 r 2 为
β 的外接圆半径
?
θ =90 2
l
l 为 α 与 β 交线: R = r 2 2
1 + r 2 ?
4
第 9 页 共 99 页
例 6( )
?
【面 α 面 β 夹角 θ =90 模型图】
分析
考查知识
答案
解答
由题意可知:平面 ABC ⊥ BCD , O 为球心, BC =l , E 为 BC 的中点,如第二个图为
例证明:(其他证明类似), OC =R ,令 O 1 一定是 △ BCD 的外接圆半径,令其为 r 1 ,
令 O 2 一定是 △ ABC 的外接圆半径,令其为 r 2 所以四边形 EO 1 OO 2 为矩形,
2 2 2 2 2 2
R =| OD | =| OO 1 | +| O 1 D| =| O 2 E | +| O 1 D|
2
1 l
=(| 2
O 2 C | -| 2 2 2 2 2 2 2
CE | )+| O 1 D| =| O 2 C | -( | BC | ) +| O 1 D| =r 1 + r 2 ?
2 4
2
l
所以 R = r 2 2
1 + r 2 ?
4
第 10 页 共 99 页
总结:?
全等三角形或者等腰拼在一起
或者菱形折叠折叠的二面角为 θ
h 为一个面的顶点到两面交线
全等三角形折叠
中点的距离
r 同一个面的外接圆半径
2 θ
R = r 2 + ( h ? r ) 2 tan
2
题型 2 全等三角形折叠
例 7( )
【全等三角形折叠模型图】
分析
考查知识
答案
解答
题设:两个全等的三角形或者等腰拼在一起,或者菱形折叠,设折叠的二面角
∠ ′ ′ ′
AEC =θ , CE =AE =h , H 1 和 H 2 分别为 △ BCD 和 △ ABD 的外接圆
BD θ
圆 心, 在 △ ′
OEC 中, CH =r = , EH 1 =h ? r , OH 1 =( h ? r ) tan ,
2 sin△ BCD
2
2 2 2 2 2 2 2 θ
2 θ
R =| OC | =| OH 1 | +| CH 1 | =r + ( h ? r ) tan 所以: R = r 2 + ( h ? r ) 2 tan
2 2
第 11 页 共 99 页
总结:?
等腰三角形底边与直角三角形斜边构成二面角为 θ
h 等腰三角形底边的高 r 等腰三角形外接圆半径
等腰底边与直角斜边
2
?
( h 2 r 2 )
R = r 2
1 +
2
sin θ
题型 3 等腰三角形底边与直角三角形斜边构成二面角的四面体
例 8( )
【等腰三角形与直角三角形斜边构成二面角的四面体】
分析
考查知识
答案
解答
凡是遇到直角三角形,通常要转换直角顶点,因为直径所对的圆周角为直角,故可将
直角顶点转换为共斜边的直角三角形直角顶点,如上图: △ ABC 以斜边 BC 为交线
与其它平面形成的二面角可以转换为平面 DBC 与其它平面构成的二面角.如上图中,
△ ABC 为等腰三角形,且 AB = AC , △ DBC 是以 BC 为斜边的 Rt △ ,二面角为 θ ,
令: △ ABC 的外接圆半径为 r 2 ,边上的高为 AO 1 =h 2 , BC =2 r 1 , F 为, △ ABC 的外心,
2 2
( h 2 ? r 2 ) ( h 2 ? r 2 )
在 △ 2 2 2 2 2
OO 1 E 中, R =| OE | =| OO 1 | +| O 1 E | =r 1 +
2 所以: R = r 2
1 +
2
sin θ sin θ
第 12 页 共 99 页
含二面角 θ 的外接球终结公式:
?
l 为 α 与 β 交线
θ 为面 α 与面 β 的夹角
为 的外接圆圆心到 中点的距离
含二面角 m α l
θ 的外接球终结公式
n 为 β 的外接圆圆心到 l 中点的距离
2 2 2
?
2 m + n 2 mncosθ l
R =
2 +
sin θ 4
例 9( )
【含二面角 θ 的外接球终结公式模型图】
分析
考查知识
答案
解答
如图,若空间四边形 C ? ABD 中,二面角的平面角大小为 θ , ABD 的外接圆圆心
为 O 1 , ABC 的外接圆圆心为 O 2 , E 为公共弦 AB 中点,则 ∠ O 1 EO 2 =θ , O 1 E =m ,
1 O 1 O 2
O 2 E =n , AE = l ,由于 O 、 O 1 、 E 、 O 2 四点共圆,且 OE =2R 1 = 根据余弦定理
2 sinθ
| 2 2 2
O 1 O 2 | =m + n ? 2 mn cosθ ,
2 2 ? 2
2 2 2 m + n 2 mncosθ l
R =| OE | +| AE | =
2 +
sin θ 4
第 13 页 共 99 页
1.2 共面问题
例 1(2020 全国 III 理 19 )
如图,在长方体 ABCD ? A1 B 1 C 1 D1 中,点 E , F 分别在棱 DD1 , BB 1 上,且 2 DE = ED 1 ,
BF = 2 F B 1 .
( I ) 证明:点 C 1 在平面 AEF 内;
分析
考查知识
答案
解答
( I ) 在 AA1 上取一三等分点 M ,使得 A1 M = 2 AM ,分
别连接 EM , B 1 M , EC 1 , F C 1 ,
在 长 方 体 ABCD ? A1 B 1 C 1 D1 中, 有
DD1 //AA1 //BB 1 ,且 DD1 = AA1 = BB 1 ,
又 2 DE = ED 1 , A1 M = 2 AM , BF = 2 F B 1 ,
所以 DE = AM = F B 1 ,即
四边形 B 1 AF M 与 EDAM 都是平行四边形
所以 AF //MB 1 且 AF = MB 1 , AD= ME 且 AD//ME ,
又在长方体中,有 AD//B 1 C 1 且 AD= B 1 C 1 ,
所以
B 1 C 1 //ME 且 B 1 C 1 = ME
则 四边形 B 1 C 1 EM 为平行四边形,
所以 EC 1 //MB 1 且 EC 1 = MB 1 ,
又
AF //MB 1 且 AF = MB 1
所以
AF //EC 1 且 AF = EC 1
则 四边形 AF C 1 E 为平行四边形,
故点 C 1 在平面 AEF 内.
第 14 页 共 99 页
1.3 平行问题
第 15 页 共 99 页
1.3.1 平行之点共面
例 1(2020 全国 III 文 19 )
如图,在长方体 ABCD ? A1 B 1 C 1 D1 中,点 E , F 分别在棱 DD1 , BB 1 上,且 2 DE = ED 1 ,
BF = 2 F B 1 .证明:
( I ) 当 AB = BC 时, EF ⊥ AC ;
( II ) 点 C 1 在平面 AEF 内.
分析
考查知识
答案
解答 ( I ) 当 AB = BC 时, EF ⊥ AC .
因为 ABCD ? A1 B 1 C 1 D1 是长方体,
所以
BB 1 ⊥ 平面 ABCD
又 AC ? 平面 ABCD ,所以
AC ⊥ BB 1
又因为 AB = BC ,所以四边形 ABCD 为正方形,
故有
AC ⊥ BD
又 BD ∩ BB 1 = B ,
所以
AC ⊥ 平面 BB 1 D1 D
又因为点 E , F 分别在棱 DD1 , BB 1 上,即 EF ? 平面 BB 1 D1 D,所以 EF ⊥ AC .
( II ) 取 AA1 靠近 A1 的三等分点 M ,连结 D1 M , C 1 F , MF ,
因为 E 在 DD1 ,且 2 DE = ED 1 ,
所以
ED 1 //AM ,且 AM = ED 1
所以四边形 AED 1 M 为平行四边形,
即有
D1 M //AE ,且 D1 M = AE
又 F 在 BB 1 上,且 BF = 2 F B 1 ,
所以 MF //A1 B 1 ,且 MF = A1 B 1 ,
故
第 16 页 共 99 页
MF //D1 C 1 , MF = D1 C 1 ,即 D1 MF C 1 为平行四边形
所以
D1 M //C 1 F , AE //C 1 F
故 A, E , F , C 1 四点共面,所以 C 1 在平面 AEF 内.
第 17 页 共 99 页
1.3.2 平行问题基础理论
平行问题基础理论: ?
1.3.3 正向平移证平行问题
总结:?
说明 :以线 (已知直线 ) 平行与面 (已知平面 ) 为核心
把已知直线沿某条直线平移到已知平面内
如何
第 一 招 :
让线过顶点或特殊点 线不超过面的轮廓
平移
正向沿线 与面的交点为点,与相应点的连线为线
找点找线
(一长一短 : 中位线定理 (相似 )
平移法
如何 一样长:平行四边形
证明
证明平行四边形常用的方法 : 一组对边平行且相等
两组对边分别平行 两组对边分别相等
第 18 页 共 99 页
1.3.4 平行的传递性
例 1(2020 北京 16 )
如图,在正方体 ABCD ? A1 B 1 C 1 D1 中, E 为 BB 1 中点.
( I ) 求证: BC 1 // 平面 AD1 E .
分析
考查知识
答案
解答
//
( I ) 在正方体 ABCD ? A1 B 1 C 1 D1 中, AB = C 1 D1 ,
所以
四边形 ABC 1 D1 为平行四边形,则 AD1 // BC 1
又因为 BC 1 ∈/ 平面 AD1 E , AD1 ? 平面 AD1 E ,
所以
BC 1 // 平面 AD1 E
例 2(2010 浙江 )
?
如图,在平行四边形 ABCD 中, AB = 2 BC , ∠ ABC = 120 . E
为线段 AB 的中点,将 △ ADE 沿直线 DE 翻折成 △ A1 DE ,
使平面 A1 DE ⊥ 平面 BCD , F 为线段 A1 C 的中点.
( I ) 求证: BF // 平面 A1 DE ;
分析
考查知识
答案
第 19 页 共 99 页
解答
证明:正向沿线找点找线平移法找到点 G ;
取 A1 D 的中点 G ,连结 GF , CE ;
由条件易知 1
F G // CD , F G = CD
2
又 1
BE // CD , BE = CD
2
所以
F G // BE , F G = BE
故四边形 BEGF 为平行四边形,所以
BF // EG
因为 EG ? 平面 A1 DE , BF ?? 平面 A1 DE ,所以 BF
平面 A1 DE
变式练 2.1(2017 全国 II 理 19 )
如图,四棱锥 P ? ABCD 中,侧面 P AD 为等边三角形且垂直于底面三角形 BCD , AB =
1 ?
BC = AD, ∠ BAD = ∠ ABC = 90 , E 是 P D 的中点.
2
( I ) 证明:直线 CE // 平面 P AB ;
变式练 2.1 分析 考查知识
变式练 2.1
解答 ( I ) 取 P A 中点 F ,连接 BF , EF ,
因为 E , F 分别为 P D , P A 中点,
所以 1
EF // AD
2
?
因为 ∠ BAD = ∠ ABC = 90 ,所以 BC //AD,
所以 1
BC // AD
2
所以
BC //EF
所以四边形 BCEF 为平行四边形,
第 20 页 共 99 页
所以
CE //BF
因为 BF ? 平面 P AB , CE ?? 平面 P AB ,
所以 CE // 平面 P AB .
例 3(2017 全国 I )
?
如图,在四棱锥 P ? ABCD 中, AB // CD ,且 ∠ BAP = ∠ CDP = 90 .
( I ) 证明:平面 P AB ⊥ 平面 P AD ;
分析
考查知识
答案
?
解答 ( I ) 因为 ∠ BAP = ∠ CDP = 90 ,
所以
P A ⊥ AB , P D ⊥ DC
又因为 AB // DC ,
所以
AB ⊥ P D
又因为 P A ∩ P D = P ,
所以 AB ⊥ 平面 P AD ,因为 AB ? 平面 P AB ,
所以
平面 P AB ⊥ 平面 P AD .
第 21 页 共 99 页
1.3.5 反向沿线找点找线平移法
总结:?
说明 :以线 (已知直线 ) 平行与面 (已知平面 ) 为核心
把己知平面上的线沿某条直线平移到已知直线
如何
构建此时相交直线所形成的面
第 二 招 :
平移
证明两个平面平行即可
反向沿线
一长一短 中位线定理 相似
( : ( )
找点找线
一样长:平行四边形
平移法
如何
证明平行四边形常用的方法
证明
一组对边平行且相等 两组对边分别平行
两组对边分别相等
例 1(2013 辽宁 )
如图, AB 是圆 O 的直径, P A 垂直圆 O 所在的平面, C 是
圆 O 上的点.
( I ) 设 Q 为 P A 的中点, G 为 ?AOC 的重心,求证: QG //
平面 P BC .
分析
考查知识
答案
第 22 页 共 99 页
解答
证明:反向平移 P C 找到点 M ;即取 AC 的中点为 M ,
连接 QM , OM , QO .由 G 为 ?AOC 的重心,得 M
为 AC 中点,由 G 为 P A 中点,得
QM // P C
又 O 为 AB 中点,得
OM // BC
因为 QM ∩ MO =M , QM ? 平面 QMO .
所以 QG // 平面 P BC .
变式练 1.1(2018 天津理 17 )
如图, AD// BC 且 AD= 2 BC , AD⊥ CD , EG // AD 且 EG = AD, CD // F G 且 CD = 2 F G ,
DG ⊥ 平面 ABCD , DA= DC = DG = 2 .
( I ) 若 M 为 CF 的中点, N 为 EG 的中点,求证: MN // 平面 CDE ;
变式练 1.1 分析 考查知识
变式练 1.1
解答 ( I ) 取 GD 的中点为 O ,
第 23 页 共 99 页
1.4 垂直问题
1.4.1 垂直问题基础理论
垂直问题基础理论:? 立体几何证明问题中的转化思想
? 直线与平面垂直的定义:如果直线 l 与平面 α 内的任意一条直线都垂直,我们就说直线 l
与平面 α 相互垂直,记作 l ⊥ α .
? 直线与平面垂直的判定与性质 :
判定定理:如果一条直线与一个平面内的两条相交直线都
垂直,那么该直线与此平面垂直 . (简记为“线线垂直 ?
线面垂直”)
a?
α
b ? α
符号语言: l ⊥ a ?l ⊥ α
l ⊥ b
a∩ b = O
性质定理:垂直于同一平面的两条直线平行;一条直线垂
直于一个平面,则这条线垂直于平面内的所有直线
符号语言: ? ?
a⊥ α a⊥ α
?a⊥ b ; ?a⊥ ? ( 任意 m, n, b ) .
b ⊥ α ? ( 任意) m, n, b ? α
? 直线与平面所成的角
平面的一条斜线和它在平重上的投影所成的锐角,叫做这
条直线和这个平面所成的角 .
注:
1. 一条直线垂直于平面,该直线与平面所成的角为直角;
2. 一条直线与平面平行或在平面内,则此直线与平面所成
?
的角是 0 的角;
3. 直线与平面所成角的范围是 π
[0, ].
2
第 24 页 共 99 页
1.4.2 垂直问题基础理论
总结:? 平面与平面垂直的判定与性质 :
1. 二面角:从一条直线出发的两个半平面所组成的图形叫
做二面角 .
2. 二面角的平面角:在二重角的棱上任取一点,以该点为
垂足,在二面角的两个半平面内分别作垂直于棱的两条射
线,这两条射 ∠ AOB 即为二面角 α ? l ? β 的平面角 .
3. 二重角的平面角的范围是 [0 , π ].
? 平面与平面垂直的定义 : 一般地,两个平面相交,如果它们所成的二面角是直二面角,就
说这两个平面互相垂直 . 面面垂直的判定定理与性质定理:
判定定理:如果一个平面经过另一个平面的垂线那么这两
个平面互相垂直(简记为“线面垂直 ? 面面垂直” )
?
l ⊥ α
符号语言: ?α ⊥ β
l ? β
性质定理:如果两个平面互相垂直,那么在一个平面内垂
直于它们交线的直线必垂直于另一个平面 (简记为“面面
垂直 ? 线面垂直” )
α ⊥ β
α ∩
β = l
符号语言: ?a⊥ α
a?
β
a⊥ l
总结:? 垂直问题基础理论
?
直角三角形——斜边上的中线
等腰梯形
垂直问题辅助线常规作法
过上顶点作线垂直于底
过底作两腰的反向延长线交于一点
第 25 页 共 99 页
1.4.3 系统法 1:面 ⊥ 面
系统法 1:面 ⊥ 面:
?
已知面垂直面
找交线
系统法 1:一面
谁垂直交线(不垂直,作垂直)
谁垂直另一个面
例 1(2018 天津 )
如图,在四面体 ABCD 中, ?ABC 是等边三角形,平面
ABC ⊥ 平面 ABD ,点 M 为棱 AB 的中点, AB = 2 , AD=
√ ?
2 3 , ∠ BAD = 90 .
( I ) 证明: AD⊥ BC .
分析
考查知识
答案
解答
由平面 ABC ⊥ 平面 ABD ;又
平面 ABC ∩ 平面 ABD = AB
且
AD⊥ AB
可得 AD⊥ 平面 ABC ,故
AD⊥ BC
变式练 1.1(2020 浙江 19 )
如图,三棱台 DEF ? ABC 中,面 ADF C ⊥ 面 ABC , ∠ ?
ACB = ∠ ACD = 45 , DC = 2 BC .
( I ) 证明: EF ⊥ DB ;
变式练 1.1 分析 考查知识
第 26 页 共 99 页
变式练 1.1
解答 ( I ) 如图,过点 D 作 DO ⊥ AC .交直线 AC 于点 O ,连结
OB . √
?
由 ∠ ACD = 45 , DO ⊥ AC 得 CD = 2 CO ,
由平面 ACF D ⊥ 平面 ABC 得 DO ⊥ 平面 ABC ,所以
DO ⊥ BC . √
由 ∠ ? 1 2
ACB = 45 , BC = CD = CO ,得 BO ⊥ BC .
2 2
所以 BC ⊥ 平面 BDO ,故 BC ⊥ DB .
变式练 1.2(2018 全国 III 理 19 )
? ?
如图,边长为 2 的正方形 ABCD 所在的平面与半圆弧 CD 所在平面垂直, M 是 CD 上异
于 C , D 的点.
( I ) 证明:平面 AMD ⊥ 平面 BMC ;
变式练 1.2 分析 考查知识
变式练 1.2
解答 ( I ) 由题设知,平面 CMD ⊥ 平面 ABCD ,交线为 CD .
因为 BC ⊥ CD , BC ? 平面 ABCD ,
所以
BC ⊥ 平面 CMD ,故 BC ⊥ DM .
?
因为 M 为 CD 上异于 C , D 的点,且 DC 为直径,
所以
DM ⊥ CM
又 BC ∩ CM = C ,所以 DM ⊥ 平面 BMC .
而 DM ? 平面 AMD ,
故平面 AMD ⊥ 平面 BMC .
第 27 页 共 99 页
1.4.4 系统法 2:二线
总结:?
两个三角形的三线合一
等腰三角形
系统法 2:二线
等边三角形
三线合一——中线,角平分线,高
例 1(2017 全国 III )
如图,四面体 ABCD 中, ?ABC 是正三角形, AD= CD .
( I ) 证明: AC ⊥ BD ;
分析
考查知识
答案
解答
证明:取 AC 的中点 O 连结 DO , BO ;
因为
AD= CD
所以
AC ⊥ DO
又由于 ?ABC 是正三角形,所以
AC ⊥ BO
从而 AC ⊥ 平面 DOB ,故 AC ⊥ BD .
第 28 页 共 99 页
变式练 1.1(2007 福建文 17 )
如图,正三棱柱 ABC ? A1 B 1 C 1 的所有棱长都为 2 , D 为
A A1
CC 1 的中点.
( I ) 求证: AB 1 ⊥ 平面 A1 BD ;
C C 1
D
B B 1
变式练 1.1 分析 考查知识
变式练 1.1
解答 ( I ) 证明:取 BC 的中点 O ,连接 AO .因为 △ ABC 为正
A A1
三角形,所以 AO ⊥ BC ;
因为正三棱柱 ABC ? A1 B 1 C 1 中,平面 ABC ⊥ 平面
BCC 1 B 1 ;
C C 1
AO ⊥ 平面 BCC 1 B 1 .连接 B 1 O ,在正方形 BB 1 C 1 C 中, D
O
O , D 分别为 BC , CC 1 的中点,所以所以 B 1 O ⊥ BD B B 1
, AO ⊥ BD .
所以 BD ⊥ 平面 AOB 1 ,则 BD ⊥ AB 1 ;
ABA 1 B 1 中, AB 1 ⊥ A1 B ,所以 AB 1 ⊥ 平面 A1 BD .
第 29 页 共 99 页
1.4.5 系统法 3:三勾股
系统法 3:三勾股:
?
勾股定理之逆定理证明垂直
常包含基本定理
系统法 3:三勾股
余弦定理
正弦定理
例 1(2010 江苏 )
如图,在三棱锥 P ? ABC 中, D, E , F 分别为棱 P C , AC ,
P
AB 的中点,已知 P A ⊥ AC , P A =6, BC =8, DF =5.
( I ) 求证:平面 BDE ⊥ 平面 ABC .
D
E C 1
A F B
分析
考查知识
答案
解答
因为 D , E 为 P C AC 中点,所以
1
DE = P A = 3
2
又因为 E , F 为 AC , AB 中点,所以
1
EF = BC = 4
2
且 DF =5,所以
2 2 2
DE + EF = DF
因为 ∠ ?
DEF = 90 ,所以
DE ⊥ EF
又因为 DE //P A P A ⊥ AC ,所以
DE ⊥ AC
又 AC ∩ EF = E ,所以 DE ⊥ 平面 ABC ,又 DE ? 平面 BDE ,所以
平面 BDE ⊥ 平面 ABC
第 30 页 共 99 页
变式练 1.1(2020 全国 I 理 18(2/5) )
如图, D 为圆锥的顶点, O 是圆锥底面的圆心, √ AE 为底面直径, AE = AD . △ ABC 是底
6
面的内接正三角形, P 为 DO 上一点, P O = DO
6
( I ) 证明 : P A ⊥ 平面 P BC
D
P
C
O
E B
A
变式练 1.1 分析 考查知识
变式练 1.1
解答 ( I ) 设 DO = a,由题设可得 √ √ √
6 3 2
P O = a, AO = a, AB = a, P A = P B = P C = a
6 3 2
2 2 2
因此 P A + P B = AB ,
从而
P A ⊥ P B
2 2 2
又 P A + P C = AC ;
故 P A ⊥ P C ,所以 P A ⊥ 平面 P BC .
变式练 1.2(2018 全国 II 文 19 ) √
如图,在三棱锥 P ? ABC 中, AB = BC = 2 2 , P A = P B = P C = AC = 4 , O 为 AC 的中
点.
( I ) 证明: P O ⊥ 平面 ABC ;
变式练 1.2 分析 考查知识
变式练 1.2
第 31 页 共 99 页
解答 ( I ) 连接 BO ,因为 P A = P C = 4 , O 为 AC 中点,
√
所以 P O ⊥ AC , P O = 2 3 ,
√
2 2
又因为 AB = BC = 2 2 , AC = 4 ,满足 AB + BC =
2
AC ,
所以 △ ABC 为等腰直角三角形,
所以 BO = 2 ,
在 △ 2 2 2
P OB 中, P B = 4 ,则 P O + BO = P B ,
则 P O ⊥ OB ,又因为 AC ∩ OB = O ,
所以 P O ⊥ 面 ABC . √
因为 AP = CP = AC = 4 , O 为 AC 的中点,所以 OP ⊥ AC ,且 OP = 2 3 .
连结 OB , √
2
因为 AB = BC = AC ,所以 △ ABC 为等腰直角三角形,且 OB ⊥ AC ,
2
1
OB = AC = 2 .
2
2 2 2
由 OP + OB = P B 知, OP ⊥ OB .
由 OP ⊥ OB , OP ⊥ AC 知 P O ⊥ 平面 ABC .
第 32 页 共 99 页
1.4.6 系统法 4:四图一柱
总结:?
四图
正方形——棱垂直棱、对角线垂直
菱形——对角线垂直
系统法 4:四图一柱 矩形——棱垂直棱
?
圆——直径所对圆周角 =90
一柱
直棱柱——侧棱垂直底面
例 1(四图一柱之正方形 )
已知四棱锥 S ? ABCD 的底面 ABCD 是正方形, SA ⊥ 底
面 ABCD , E 是 SC 上的任意一点 .
( I ) 求证:平面 EBD // 平面 SAC .
分析
考查知识
答案
解答
证明: SA ⊥ 平面 ABCD , BD ? 平面 ABCD ,所以
SA ⊥ BD
因为 ABCD 是正方形,所以
AC ⊥ BD
所以 BD ⊥ 平面 SAC ,又因为 BD ? 平面 EBD ;
所以
平面 EBD ⊥ 平面 SAC
第 33 页 共 99 页
变式练 1.1(2020 海南 20 )
如图,四棱锥 P ? ABCD 的底面为正方形, P D ⊥ 底面 ABCD .设平面 P AD 与平面 P BC
的交线为 l .
( I ) 证明: l ⊥ 平面 P DC ;
变式练 1.1 分析 考查知识
变式练 1.1
解答 ( I ) 在正方形 ABCD 中, AD// BC ,
因为
AD?? 平面 P BC , BC ? 平面 P BC
所以 AD// 平面 P BC ,
又因为 AD? 平面 P AD ,平面 P AD ∩ 平面 P BC = l ,
所以 AD// l ,
因为在四棱锥 P ? ABCD 中,底面 ABCD 是正方形,所以 AD⊥ DC ,
所以
l ⊥ DC ,且 P D ⊥ 平面 ABCD
所以 AD⊥ P D ,所以 l ⊥ P D ,
因 CD ∩ P D = D,所以 l ⊥ 平面 P DC .
变式练 1.2(2018 全国 I 理 18 )
如图,四边形 ABCD 为正方形, E, F 分别为 AD, BC 的中点,以 DF 为折痕把 △ DF C
折起,使点 C 到达点 P 的位置,且 P F ⊥ BF .
( I ) 证明:平面 P EF ⊥ 平面 ABF D ;
变式练 1.2 分析 考查知识
变式练 1.2
第 34 页 共 99 页
解答 ( I ) 证明:因为 E , F 分别为 AD, BC 的中点,四边形 ABCD 为正方形
所以 EF // AB , BC ⊥ AB ;
所以
BC ⊥ EF
因为 P F ⊥ BF ,
所以 P F ⊥ BC ,
而: EF ∩ P F = F
所以
BC ⊥ 平面 P EF
而: BC ? 平面 ABF D ,
∴ 平面 P EF ⊥ 平面 ABF D .
例 2(四图一柱之菱形 )
如图四边形 ABCD 为菱形, G 为 AC 与 BD 交点, BE ⊥
E
平面 ABCD .
( I ) 证明:平面 AEC ⊥ 平面 BED .
D C
A G
B
分析
考查知识
答案
解答
因为四边形 ABCD 为菱形,所以
AC ⊥ BD
因为 BE ⊥ 平面 ABCD ,所以
AC ⊥ BE
故 AC ⊥ 平面 BED .又 AC ? 平面 AEC ,所以
平面 AE ⊥ 平面 BED
第 35 页 共 99 页
四图一柱之圆
例 3(2013 辽宁 )
如图, AB 是圆 O 的直径, P A 垂直圆 O 所在的平面, C 是
圆 O 上的点.
( I ) 求证: BC ⊥ P AC .
分析
考查知识
答案
解答 证明:由 AB 是圆 O 的直径,得
AC ⊥ BC
由 P A ⊥ 平面 ABC , BC ? 平面 ABC ,得
P A ⊥ BC
又 P A ∩ AC = A, P A ? 平面 P AC , AC ? 平面 P AC ,所以
BC ⊥ 平面 P AC
变式练 3.1(2020 全国 II 理 20(4/5) )
如图 , 已知三棱柱 ABC ? A1 B 1 C 1 的底面是正三角形 , 侧面 BB 1 C 1 C 是矩形 , M , N 分别为
BC , B 1 C 1 的中点 , P 为 AM 上一点 . 过 B 1 C 1 和 P 的平面交 AB 于 E , 交 AC 于 F .
( I ) 证明 : AA1 // MN , 且平面 A1 AMN ⊥ 平面 EB 1 C 1 F ;
C 1
A1 O N
B 1
F C
A E P M
B
变式练 3.1 分析 考查知识
第 36 页 共 99 页
变式练 3.1
解答 ( I ) 因为 M, N 分别为 BC , B 1 C 1 的中点,所以
MN // CC 1
又由已知得 AA1 // CC 1 , 故
AA1 // MN
因为 △ A1 B 1 C 1 是正三角形,
所以 B 1 C 1 ⊥ A1 N . 又 B 1 C 1 // MN ,
故
B 1 C 1 ⊥ 平面 A1 AMN . 所以平面 A1 AMN ⊥ 平面 EB 1 C 1 F
第 37 页 共 99 页
1.4.7 系统法 5:五射影
总结:? ?
射影定理
系统法 5:五射影
点到射影面的射影线垂直射影面
例 1(五射影 )
如 图, 在 斜 三 棱 柱 ABC ? A1 B 1 C 1 中, AB = BC = 2 ,
∠ ?
ABC =120 ,又顶点 A1 在底面 ABC 上的射影落在 AC
上, M 为 AC 的中点
( I ) 求证: AA1 ⊥ BD .
分析
考查知识
答案
解答
在斜三棱柱 ABC ? A1 B 1 C 1 中,因为 A1 在底面 ABC 上的射影落在 AC 上,则平面
A1 ACC 1 经过底面 ABC 的垂线,故
侧面 A1 C ⊥ 平面 ABC
又因为侧面 A1 C ∩ 面 ABC =AC ,又 BD 为等腰 △ ABC 底边 AC 上中线,则
BD ⊥ AC
从而
BD ⊥ 平面 A1 C
又因为 AA1 ? 平面 A1 C ,所以
AA1 ⊥ BD
第 38 页 共 99 页
1.4.8 系统法 6:转化
总结:?
平行的传递性
垂直于同一平面的两条直线互相平行
系统法 6:六转化
两条直线互相平行,若其中一条垂直一个平面
则另一条直线也垂直于该平面
例 1(六转化 2015 新课标 )
如图,四边形 ABCD 为菱形, G 为 AC 与 BD 的交点, E
z
平面 ABCD .
E
( I ) 求证:平面 AEC ⊥ 平面 BED . F
H
B A y
OO G
O
C D
x
分析
考查知识
答案
解答
例题解答
第 39 页 共 99 页
1.4.9 平行垂直综合
例 1(2020 江苏 15 )
在三棱柱 ABC ? A1 B 1 C 1 中, AB ⊥ AC , B 1 C ⊥ 平面 ABC , E , F 分别是 AC , B 1 C 的中点.
( I ) 求证: EF // 平面 AB 1 C 1 ;
( II ) 求证:平面 AB 1 C ⊥ 平面 ABB 1 .
分析
考查知识
答案
解答
( I ) 因为 E , F 分别是 AC , B 1 C 的中点,所以 EF 是三角形 AB 1 C 的中位线,
所以
EF //AB 1
因为 EF ?? 平面 AB 1 C 1 , AB 1 ? 平面 AB 1 C 1 ,
所以
EF // 平面 AB 1 C 1
( II ) 因为 B 1 C ⊥ 平面 ABC , AB ? 面 ABC ,
所以
B 1 C ⊥ AB
又因为 AB ⊥ AC , AC ∩ B 1 C = C , AC ? 面 AB 1 C , B 1 C ? 面 AB 1 C ,
所以
AB ⊥ 面 AB 1 C
因为 AB ? 面 ABB 1 ,
所以
平面 AB 1 C ⊥ 平面 ABB 1
变式练 1.1(2019 北京文 18 )
如图,在四棱锥 P ? ABCD 中, P A ⊥ 平面 ABCD ,底面 ABCD 为菱形. E 为 CD 的中
点.
( I ) 求证: BD ⊥ 平面 P AC ;
?
( II ) 若 ∠ ABC = 60 ,求证:平面 P AB ⊥ 平面 P AE ;
(III) 棱 P B 上是否存在点 F ,使得 CF // 平面 P AE ?说明理由.
第 40 页 共 99 页
变式练 1.1 分析 考查知识
变式练 1.1
解答 ( I ) P A ⊥ 平面 ABCD ,且 BD ? 平面 ABCD ,
所以
P A ⊥ BD
在菱形 ABCD 中, AC ⊥ BD ,
即
P A ⊥ BD , P A ? 平面 P AC
AC ⊥ BD , AC ? 平面 P AC , P A ∩ AC = A,
所以
BD ⊥ 平面 P AC
( II ) P A ⊥ 平面 ABCD ,且 AE ? 平面 ABCD ,
所以
P A ⊥ AE
?
在菱形 ABCD 中, ∠ ABC = 60 ,
即 ∠ ?
ADC = 60
所以 △ ADC 为等边三角形,且 E 为 CD 中点.
所以
AE ⊥ CD
又 AB //CD , AE ⊥ AB ,
即
AE ⊥ P A , P A ? 平面 P AB
AE ⊥ AB , AB ? 平面 P AB , P A ⊥ AB = A,所以
AE ⊥ 平面 P AB ,且 AE ? 平面 P AE
所以平面 P AB ⊥ 平面 P AE .
第 41 页 共 99 页
(III) 棱 AB 上存在 F 点,且 F 为 P B 的中点,取 P A 中点
为 M ,
连接 MF 、 ME 、 F C ,因为 MF 分别 P A 、 P B 中点.
所以 1
MF //AB , MF = AB
2
因为底面 ABCD 为菱形,
所以 1
CE //AB , CE = AB
2
所以
MF //CE
所以四边形 MF CE 为平行四边形,
所以
F C //EM
因为 EM ? 平面 P AE , F C ?? 平面 P AE ,
所以
F C // 平面 P AE
变式练 1.2(2019 江苏 16 )
如图,在直三棱柱 ABC ? A1 B 1 C 1 中, D, E 分别为 BC , AC 的中点, AB = BC .求证:
( I ) A1 B 1 // 平面 DEC 1 ;
( II ) BE ⊥ C 1 E .
变式练 1.2 分析 考查知识
变式练 1.2
解答 ( I ) 因为 D, E 分别为 BC , AC 的中点,所以
ED // AB
在直三棱柱 ABC ? A1 B 1 C 1 中, AB // A1 B 1 ,
所以
A1 B 1 // ED
又因为 ED ? 平面 DEC 1 , A1 B 1 ?? 平面 DEC 1 ,
所以 A1 B 1 // 平面 DEC 1 .
因为 D, E 分别为 BC , AC 的中点,
第 42 页 共 99 页
所以
ED // AB
在直三棱柱 ABC ? A1 B 1 C 1 中, AB // A1 B 1 ,
所以
A1 B 1 // ED
又因为
ED ? 平面 DEC 1 , A1 B 1 ?? 平面 DEC 1
所以
A1 B 1 // 平面 DEC 1
( II ) 因为 AB = BC , E 为 AC 的中点,所以 BE ⊥ AC .
因为三棱柱 ABC ? A1 B 1 C 1 是直棱柱,所以 C 1 C ⊥ 平面 ABC .
又因为 BE ? 平面 ABC ,所以 C 1 C ⊥ BE .
因为
C 1 C ? 平面 A1 ACC 1 , AC ? 平面 A1 ACC 1 , C 1 C ∩ AC = C
所以 BE ⊥ 平面 A1 ACC 1 ,
因为 C 1 E ? 平面 A1 ACC 1 ,所以 BE ⊥ C 1 E .
变式练 1.3(2018 全国 III )
如图,矩形 ? ?
ABCD 所在的平面与半圆弧 CD 所在平面垂直, M 是 CD 上异于 C , D 的点.
( I ) 证明:平面 AMD ⊥ 平面 BMC ;
( II ) 在线段 AM 上是否存在点 P ,使得 MC // 平面 P BD ?说明理由.
变式练 1.3 分析 考查知识
变式练 1.3
解答 ( I ) 由题设知,平面 CMD ⊥ 平面 ABCD ,交线为 CD .
因为 BC ⊥ CD , BC ? 平面 ABCD ,
所以
BC ⊥ 平面 CMD ,故 BC ⊥ DM .
因为 ?
M 为 CD 上异于 C , D 的点,且 DC 为直径
所以 DM ⊥ CM .
又 BC ∩ CM = C ,所以
DM ⊥ 平面 BMC .
而 DM ? 平面 AMD ,故平面 AMD ⊥ 平面 BMC .
第 43 页 共 99 页
( II ) 当 P 为 AM 的中点时, MC // 平面 P BD .
证明如下:
连结 AC 交 BD 于 O .
因为 ABCD 为矩形,所以 O 为 AC 中点.
连结 OP ,因为 P 为 AM 中点,所以 MC // OP .
MC ?? 平面 P BD , OP ? 平面 P BD ,所以 MC // 平面
P BD .
变式练 1.4(2018 江苏 15 )
在平行六面体 ABCD ? A1 B 1 C 1 D1 中, AA1 = AB , AB 1 ⊥ B 1 C 1 .
( I ) 求证: AB // 平面 A1 B 1 C ;
( II ) 平面 ABB 1 A1 ⊥ 平面 A1 BC .
变式练 1.4 分析 考查知识
变式练 1.4
解答 ( I ) 因为平行六面体 ABCD ? A1 B 1 C 1 D1 .
所以面 ABC // 面 A1 B 1 C 1 D1 .
因为 A? B 面 ABCD .
所以 AB // 面 A1 B 1 C 1 D1 .
又面 ABA 1 B 1 ∩ 面 A1 B 1 C 1 D1 = A1 B 1 .
且 AB ? 面 ABA 1 B 1 .
所以 AB // A1 B 1 .
又 A1 B 1 ? 面 A1 B 1 C , AB ?? 面 A1 B 1 C .
所以 AB // 面 A1 B 1 C .
( II ) 由( 1 )可知: BC // B 1 C 1 .
因为 AB 1 ⊥ B 1 C 1 .
所以 AB 1 ⊥ BC .
因为平行六面体 ABCD ? A1 B 1 C 1 D1 .
所以 AB = A1 B 1 .
又由( 1)得 AB // A1 B 1 .
所以四边形 ABB 1 A1 为平行四边形.
第 44 页 共 99 页
因为 AA1 = AB 1 .
所以平行四边形 ABB 1 A1 为菱形.
所以 AB 1 ⊥ A1 B .
又 A1 B ∩ BC = C .
所以 AB 1 ⊥ 面 A1 BC .
因为 AB 1 ? 面 ABB 1 A1 .
所以面 ABB 1 A1 ⊥ 面 A1 BC .
变式练 1.5(2018 北京文 18 )
如图,在四棱锥 P ? ABCD 中,底面 ABCD 为矩形,平面 P AD ⊥ 平面 ABCD , P A ⊥ P D ,
P A = P D , E , F 分别为 AD, P B 的中点.
( I ) 求证: P E ⊥ BC ;
( II ) 求证:平面 P AB ⊥ 平面 P CD ;
(III) 求证: EF // 平面 P CD .
变式练 1.5 分析 考查知识
变式练 1.5
解答 ( I ) 在 △ P AD 中, P A = P D ,点 E 为 AD 中点,
所以 P E ⊥ AD ,
因为平面 P AD ⊥ 平面 ABCD ,
平面 P AD ∩ 平面 ABCD = AD , P E ? 平面 P AD ,
所以 P E ⊥ 平面 ABCD
因为 BC ? 平面 ABCD ,
所以 P E ⊥ BC .
( II ) 由( 1 )知 P E ⊥ 平面 ABCD ,
因为 CD ? 平面 ABCD ,
所以 P E ⊥ CD ,
又 CD ⊥ AD, P E , AD? 平面 P AD , P E ∩ AD= E ,
所以 CD ⊥ 平面 P AD ,
因为 P A ? 平面 P AD ,所以 CD ⊥ P A ,
因为 P A ⊥ P D , CD , P D ? 平面 P CD , CD ∩ P D = D,
所以 P A ⊥ 平面 P CD .
第 45 页 共 99 页
因为 P A ? 平面 P AB ,
所以平面 P AB ⊥ 平面 P CD .
(III) 取 P C 中点 Q ,连接 F Q , DQ ,
在 △ P BC 中, F , Q 分别为 P B , P C 中点,
所以 1
F Q // BC ,且 F Q = BC ,
2
因为 1
ED // BC ,且 ED = BC ,
2
所以 F Q // ED ,且 ED = F Q ,
所以四边形 EF QD 为平行四边形,
所以 EF // DQ , EF ?? 平面 P CD , DQ ? 平面 P CD ,
所以 EF // 平面 P CD .
变式练 1.6(2017 山东文 18 )
由四棱柱 ABCD ? A1 B 1 C 1 D1 截去三棱锥 C 1 ? B 1 CD 1 后得到的几何体如图所示,四边形
ABCD 为正方形, O 为 AC 与 BD 的交点, E 为 AD 的中点, A1 E ⊥ 平面 ABCD .
( I ) 证明: A1 O // 平面 B 1 CD 1 ;
( II ) 设 M 是 OD 的中点,证明:平面 A1 EM ⊥ 平面 B 1 CD 1 .
变式练 1.6 分析 考查知识
变式练 1.6
解答 ( I ) 证:取 B 1 D1 中点 F ,连接 A1 F , CF ,
因为 ABCD ? A1 B 1 C 1 D1 为四棱柱,
所以 A1 F // OC, A 1 F = OC ,
所以四边形 A1 F CO 为平行四边形,
所以 A1 O // CF ,
又 CF ? 平面 B 1 CD 1 , A1 O ?? 平面 B 1 CD 1 ,
所以 AO // 平面 B 1 CD 1 .
( II ) 因为 E 为 AD 的中点, M 为 OD 的中点,
所以 EM // AO ,因为四边形 ABCD 为正方形,
所以 AO ⊥ BD ,所以 EM ⊥ BD ,
又 A1 E ⊥ 平面 ABCD ,
所以 A1 E ⊥ BD ,所以 BD ⊥ 平面 A1 EM ,
又因为 B 1 D1 ? 平面 B 1 D1 C, BD // B 1 D1 ,
∴ B 1 D1 ⊥ 平面 A1 EM ,
第 46 页 共 99 页
又 B 1 D1 ? 平面 B 1 CD 1 ,
所以平面 A1 EM ⊥ 平面 B 1 CD 1 .
变式练 1.7(2017 北京文 18 )
如图,在三棱锥 P ? ABC 中, P A ⊥ AB , P A ⊥ BC , AB ⊥ BC , P A = AB = BC = 2 , D 为
线段 AC 的中点, E 为线段 P C 上一点.
( I ) 求证: P A ⊥ BD ;
( II ) 求证:平面 BDE ⊥ 平面 P AC ;
(III) 当 P A // 平面 BDE 时,求三棱锥 E ? BCD 的体积.
变式练 1.7 分析 考查知识
变式练 1.7
解答 ( I ) 因为 P A ⊥ AB , P A ⊥ BC , AB ∩ BC = B , AB , BC ? 平面 ABC .
所以
P A ⊥ 平面 ABC
因为
BD ? 平面 ABC
所以
P A ⊥ BD
( II ) 因为 AB = BC , D 为 AC 中点,
所以
BD ⊥ AC
又因为 BD ⊥ P A , P A ∩ AC = A,
所以 BD ⊥ 平面 P AC
因为
BD ? 平面 BDE
所以平面 BDE ⊥ 平面 P AC
(III) 因为 P A // 平面 BDE ,平面 P AC ∩ 平面 BDE = DE
所以 P A // DE ,
因为 P A ⊥ 平面 ABC ,
所以 DE ⊥ 平面 ABC
S △ 1 1
ABC = DC × BD = 1 , DE = P A = 1 ,
2 2
所以 1 1
V E ? BCD = S △ ABC × DE = .
3 3
因为 P A // 平面 BDE , P A ? 平面 P AC ,平面 P AC ∩ 平面 BDE = DE ,
所以 P A //DE ,
又 D 为 AC 中点, P A //DE ,
所以 DE 为 △ 1
CP A 中位线, E 为 P C 中点,且 DE = P A = 1 ,
2
由( 1 )得 P A ⊥ 平面 ABC , P A //DE ,
第 47 页 共 99 页
DE ⊥ 平面 ABC ,
所以 DE 为三棱锥 E ? BCD 的高,所以 1
V E ? BCD = | DE | · S △ BCD ,
3
1 1 1
S △ BCD = S △ ABC = · · 2 · 2 = 1 ,
2 2 2
1 1
V E ? BCD = · 1 · 1 = ,
3 3
所以三棱锥 E ? 1
BCD 的体积为 .
3
第 48 页 共 99 页
1.5 立体几何与空间向量
例 1(2018 上海 17 )
已知圆锥的顶点为 P ,底面圆心为 O ,半径为 2 .
( I ) 设圆锥的母线长为 4 ,求圆锥的体积.
?
( II ) 设 P O = 4 , OA , OB 是底面半径,且 ∠ AOB = 90 , M 为线段 AB 的中点,如图,求
异面直线 P M 与 OB 所成的角的大小(正切值).
分析
考查知识
答案
解答 √ √
( I ) h = 4 2 ? 2 2 = 2 3 , √
所以 1 2 8 3 π
V = πr h =
3 3
( II ) 取 OA 的中点 N ,
所以等价于求 ∠ P MN .
则 √ √
1
MN = OB = 1 , P N = P O 2 + ON 2 = 17
√ 2 √
所以 P N
tanθ = = 17 所以 θ = arc tan 17 .
MN
第 49 页 共 99 页
1.5.1 空间向量与线线角
例 1(2018 江苏 25 )
如图,在正三棱柱 ABC ? A1 B 1 C 1 中, AB = AA1 = 2 ,点 P , Q 分别为 A1 B 1 , BC 的中点.
( I ) 求异面直线 BP 与 AC 1 所成角的余弦值;
分析
考查知识
答案
解答
( I ) 设 AC , A1 C 1 的中点分别为 O , O 1 ,
则 OB ⊥ OC , OO 1 ⊥ OC , OO 1 ⊥ OB ,
# ? # ? # ?
故以 {OB, OC, OO 1 } 为基底,
建立空间直角坐标系 O ? xyz ,
因为 AB = AA1 = 2 , A(0 ,? 1 ,0) ,
√ √
B ( 3 ,0 ,0) , C (0 ,1 ,0) , A1 (0 ,? 1 ,2) , B 1 ( 3 ,0 ,2) ,
C 1 (0 ,1 ,2) .
点 P 为 √A1 B 1 的中点.
3
所以 1
P ( ,? ,2) ,
2 2 √
所以
# ? 3 1 # ?
BP = ? ,? ,2 , AC 1 = (0 ,2 ,2) .
2 2
# ? # ? √
# ? # ? | BP · AC | | ? 1 + 4 |
| 1 3 10
cos< BP , AC 1 > | = # ? # ? = √ √ = .
| BP | · | AC 1 | 5 × 2 2 20
√
3 10
所以异面直线 BP 与 AC 1 所成角的余弦值为: .
20
第 50 页 共 99 页
1.5.2 空间向量与点到面的距离
例 1(2019 上海 17 )
如图,在长方体 ABCD ? A1 B 1 C 1 D1 中, M 为 BB 1 上一点,已知 BM = 2 , CD = 3 , AD= 4 ,
AA1 = 5 .
( I ) 求直线 A1 C 与平面 ABCD 的夹角;
( II ) 求点 A 到平面 A1 MC 的距离.
分析
考查知识
答案
解答
( I ) 连接 AC , A1 C ,在长方体 ABCD ? A1 B 1 C 1 D1 中,
?
AA1 ⊥ AC ,所以 ∠ A1 AC = 90 ,因为 AD= 4 , CD = 3 ,
所以 AC = 5 ;
故
?
AC = AA1 , △ A1 AC 为等腰直角三角形, ∠ A1 CA = 45
?
故 A1 C 与平面 ABCD 所成的角 ∠ A1 CA = 45 .
( II ) 以 D 为中心, DA 为 x 轴, DC 为 y 轴, DD1 为 z
轴建立空间坐标系,
# ?
则 A1 (4 ,0 ,5) , C (0 ,3 ,3) , M (4 ,3 ,2) , A1 C = ( ? 4 ,3 ,? 5) ,
# ?
MC = ( ? #?
4 ,0 ,? 2) 设平面 A1 MC 的法向量 n =
( x, y, z
) ,
#? # ?
n · A1 C = 0 ? 4 x + 3 y ? 5 z = 0
则 即 ,
#? # ?
n · MC = 0 ? 4 x ? 2 z = 0
#? # ?
解得 n = ( ? 1 ,2 ,2) , A(4 ,0 ,0) , AC = ( ? 4 ,3 ,0) ,
# ?
# ? # ? #?
#? ·
故 A 到平面 A1 MC 的距离 = | AC | AC n 10
cos< AC, n > = = .
| #?n | 3
第 51 页 共 99 页
1.5.3 定义法与角度问题
例 1(2018 天津文 17 )
如图,在四面体 ABCD 中, △ ABC 是等边三角形,平面 ABC ⊥ 平面 ABD ,点 M 为棱
√ ?
AB 的中点, AB = 2 , AD= 2 3 , ∠ BAD = 90 .
( I ) 求证: AD⊥ BC ;
( II ) 求异面直线 BC 与 MD 所成角的余弦值;
(III) 求直线 CD 与平面 ABD 所成角的正弦值.
分析
考查知识
答案
解答 ( I ) 证明:由平面 ABC ⊥ 平面 ABD ,
平面 ABC ∩ 平面 ABD = AB ,
因为
AD⊥ AB
可得 AD⊥ 平面 ABC ,
故 AD⊥ BC .
( II ) 取棱 AC 的中点 N ,连接 MN , ND .
又因为 M 为棱 AB 的中点,故 MN // BC ,
所以 ∠ DMN (或其补角)为异面直线 BC 与 MD 所成
的角. √
在 Rt△ DAM 中, AM = 1 ,故 DM = AD2 + AM 2 =
√
13 .
因为 AD⊥ 平面 ABC ,
所以 AD⊥ AC ,
在 Rt△ DAN 中, AN = 1 ,
所以 √ √
DN = AD2 + AN 2 = 13
所以在等腰三角形 DMN 中, MN = 1 ,
可得 1 √
MN
2 13
cos∠ DMN = =
DM√ 26
13
所以异面直线 BC 与 MD 所成角的余弦值为 .
26
第 52 页 共 99 页
(III) 连接 CM ,因为 △ ABC 为等边三角形, M 为边 AB 的
中点, √
所以 CM ⊥ AB , CM = 3 ,
又因为平面 ABC ⊥ 平面 ABD ,而 CM ? 平面 ABC ,
所以 CM ⊥ 平面 ABD ,
即
∠ CDM 为直线 CD 与平面 ABD 所成的角.
√
在 Rt△ CAD 中, CD = AC 2 + AD2 = 4 √ .
3
在 CM
Rt△ CMD 中, sin∠ CDM = = .
CD 4 √
3
所以直线 CD 与平面 ABD 所成角的正弦值为 .
4
第 53 页 共 99 页
1.5.4 空间向量与线面角
例 1(2020 北京 16 )
如图,在正方体 ABCD ? A1 B 1 C 1 D1 中, E 为 BB 1 中点.
( I ) 求证: BC 1 // 平面 AD1 E .
( II ) 求直线 AA1 与平面 AD1 E 所成角的正弦值.
分析
考查知识
答案
解答
//
( I ) 在正方体 ABCD ? A1 B 1 C 1 D1 中, AB = C 1 D1 ,
所以四边形 ABC 1 D1 为平行四边形,则 AD1 // BC 1 ,
又因为 BC 1 ∈/ 平面 AD1 E , AD1 ? 平面 AD1 E ,
所以 BC 1 // 平面 AD1 E .
( II ) 在正方体 ABCD ? A1 B 1 C 1 D1 中,
AA1 ⊥ 平面 ABCD , AD⊥ AB ,
所以建立以 A为坐标原点, AD 所在直线为 x 轴, AB
所在直线为 y 轴, AA1 所在直线为 z 轴的空间直角
坐标.
设正方体 ABCD ? A1 B 1 C 1 D1 的边长为 2 ,
A(0 ,0 ,0) , A1 (0 ,0 ,2) , D1 (2 ,0 ,2) , E (0 ,2 ,1) ,
# ? # ? # ?
AA1 = (0 ,0 ,2) , AD1 = (2 ,0 ,2) , AE = (0 ,2 ,1) ,
#?
设平面
AD1 E 的法向量为 n
= ( x, y, z ) ,
#? # ?
n · AD1 = 0 2 x + 2 z = 0
所以 ,所以 ,令 y = 1 ,则 x = 2 , z = ? 2 ,
#? # ?
n · AE = 0 2 y + z = 0
#?
所以 n = (2 ,1 ,? 2) ,
设直线 AA1 与平面 AD1 E 所成的角为 θ ,
所以 # ?
# ?
#?
#?
AA1 · n ? 4
2
sinθ = | cos< AA1 , n > | =
# ?
= √
=
| #?
AA1 || n | 2 × 4 + 1 + 4 3
所以直线 2
AA1 与平面 AD1 E 所成角的正弦值为 .
3
第 54 页 共 99 页
变式练 1.1(2020 全国 II 理 20(4/5) )
如图 , 已知三棱柱 ABC ? A1 B 1 C 1 的底面是正三角形 , 侧面 BB 1 C 1 C 是矩形 , M , N 分别为
BC , B 1 C 1 的中点 , P 为 AM 上一点 . 过 B 1 C 1 和 P 的平面交 AB 于 E , 交 AC 于 F .
( I ) 证明 : AA1 // MN , 且平面 A1 AMN ⊥ 平面 EB 1 C 1 F ;
( II ) 设 O 为 △ A1 B 1 C 1 的中心 , 若 AO // 平面 EB 1 C 1 F , 且 AO = AB , 求直线 B 1 E 与平面
A1 AMN 所成角的正弦值 .
C 1
A1 O N
B 1
F C
A E P M
B
变式练 1.1 分析 考查知识
变式练 1.1
解答 ( I ) 因为 M, N 分别为 BC ,B 1 C 1 的中点 , 所以 MN // CC 1 . 又由已知得 AA1 // CC 1 , 故
AA1 // MN .
因为 △ A1 B 1 C 1 是正三角形 , 所以 B 1 C 1 ⊥ A1 N . 又 B 1 C 1 // MN , 故 B 1 C 1 ⊥ 平面
A1 AMN . 所以平面 A1 AMN ⊥ 平面 EB 1 C 1 F
# ?
( II ) 由已知得 AM ⊥ BC .以 M 为坐标原点, MA 的方向为
# ?
x 轴正方向, | MB | 为单位长,建立如图所示的空间直角
坐标系 M ? xyz , √
则 AB = 2 , AM = 3 ,连结 NP ,则四边形 AONP 为
平行四边形, √ √
2 3 2 3
故 1
P M = , E , ,0 ?? ,
3 3 3
由( 1 )知平面 A1 AMN ⊥ 平面 ABC .
作 NQ ⊥ AM ,垂足为 Q
,则 NQ ⊥ 平面 ABC .
√
2 √
2
2 3 2 3
设 Q ( a,0 ,0) ,则 NQ = 4 ? ? a , B 1 a,1 , 4 ? ? a ,
3 3
√ √
√
# ? 2
2 3 2 3 # ? 2 10
故 2
B 1 E = ? a,? ,? 4 ? ? a , B 1 E = ,
3 3 3 3
#?
又 n = (0 ,? 1 ,0) 是平面 A1 AMN 的法向量,
√
#? # ?
#? # ?
#? # ?
n · B E 10
故 π 1
sin ? n ?,B 1 E = cos n ?B 1 E =
# ?
2 | #?
= .
n | · B 1 E 10
√
10
所以直线 B 1 E 与平面 A1 AMN 所成角的正弦值为 .
10
第 55 页 共 99 页
变式练 1.2(2020 浙江 19 )
?
如图,三棱台 DEF ? ABC 中,面 ADF C ⊥ 面 ABC , ∠ ACB = ∠ ACD = 45 , DC = 2 BC .
( I ) 证明: EF ⊥ DB ;
( II ) 求 DF 与面 DBC 所成角的正弦值.
变式练 1.2 分析 考查知识
变式练 1.2
解答 ( I ) 如图,过点 D 作 DO ⊥ AC .交直线 AC 于点 O ,连结
OB . √
由 ∠ ?
ACD = 45 , DO ⊥ AC 得 CD = 2 CO ,
由平面 ACF D ⊥ 平面 ABC 得 DO ⊥ 平面 ABC ,所以
DO ⊥ BC . √
由 ∠ ? 1 2
ACB = 45 , BC = CD = CO ,得 BO ⊥ BC .
2 2
所以 BC ⊥ 平面 BDO ,故 BC ⊥ DB .
( II ) 由三棱台 ABC ? DEF 得 BC //EF ,所以 EF ⊥ DB .
过点 O 作 OH ⊥ BD ,交直线 BD 于点 H ,连结 CH .
由三棱台 ABC ? DEF 得 DF //CO ,所以直线 DF 与
平面 DBC 所成角等于直线 CO 与平面 DBC 所成角.
由 BC ⊥ 平面 BDO 得 OH ⊥ BC ,故 OH ⊥ 平面 BCD ,
所以 ∠ OCH 为直线 CO 与平面 DBC 所成角.
√
设 CD = 2 2 , √ √
由 DO = OC = 2 , BO = BC = 2 ,得 BD = 6 , OH =
√
2 3
3 √
3
所以 OH
sin∠ OCH = = ,
OC 3 √
3
因此,直线 DF 与平面 DBC 所成角的正弦值为 .
3
由三棱台 ABC ? DEF 得 DF //CO ,所以直线 DF 与平面 DBC 所成角等于直线 CO
与平面 DBC 所成角,记为 θ .
如图,以 O 为原点,分别以射线 OC , OD 为 y , z 轴的正半轴,建立空间直角坐标系
O ? xyz . √
设 CD = 2 2 .
由题意知各点坐标如下.
第 56 页 共 99 页
O (0 ,0 ,0) , B (1 ,1 ,0) , C (0 ,2 ,0) , D(0 ,0 ,2) .
# ? # ? # ?
因此 OC = (0 ,2 ,0) , BC = ( ? 1 ,1 ,0) , CD = (0 ,? 2 ,2) ,
设平面
BCD 的法向量
n = ( x, y, z ) .
# ?
n · BC = 0 ? x + y = 0
由 ,即 ,可取 n = (1 ,1 ,1) ,
# ?
n · CD = 0 ? 2 y + 2 z = 0
# ? √
# ? | OC · n |
所以 sinθ = | 3
cos< OC , n > | = # ? = .
| OC | · | n | 3 √
3
因此,直线 DF 与平面 DBC 所成角的正弦值为 .
3
变式练 1.3(2020 海南 20 )
如图,四棱锥 P ? ABCD 的底面为正方形, P D ⊥ 底面 ABCD .设平面 P AD 与平面 P BC
的交线为 l .
( I ) 证明: l ⊥ 平面 P DC ; √
( II ) 已知 P D = AD= 1 , Q 为 l 上的点, QB = 2 ,求 P B 与平面 QCD 所成角的正弦值.
变式练 1.3 分析 考查知识
变式练 1.3
解答 ( I ) 在正方形 ABCD 中, AD// BC ,
因为
AD?? 平面 P BC , BC ? 平面 P BC
所以 AD// 平面 P BC ,
又因为 AD? 平面 P AD ,平面 P AD ∩ 平面 P BC = l ,
所以 AD// l ,
因为在四棱锥 P ? ABCD 中,底面 ABCD 是正方形,所以 AD⊥ DC ,
所以
l ⊥ DC ,且 P D ⊥ 平面 ABCD
所以 AD⊥ P D ,所以 l ⊥ P D ,
因 CD ∩ P D = D,所以 l ⊥ 平面 P DC .
第 57 页 共 99 页
( II ) 如图建立空间直角坐标系 D? xyz ,因为 P D = AD= 1 ,
则 有 D(0 ,0 ,0) , C (0 ,1 ,0) , A(1 ,0 ,0) , P (0 ,0 ,1) ,
B (1 ,1 ,0) ,
# ? # ? # ?
设 Q ( m, 0 ,1) ,则有 DC = (0 ,1 ,0) , DQ = ( m, 0 ,1) , P B =
(1 ,1 ,? 1) , √
因为 QB ?
= 2 , √
2 2 2
所以有 ( m ? 1) + (0 ? 1) + (1 ? 0) = 2 ?m = 1 ,
#?
设平面
QCD 的法向量为
n = ( x, y, z ) ,
# ? #?
DC · n = 0 y = 0
则
# ? ,即 ,
#?
DQ · n = 0 x + z = 0
#?
令 x = 1 ,则 z = ? 1 ,所以平面 QCD 的一个法向量为 n = (1 ,0 ,? 1) ,
# ? √
#? # ? #? · 6
则 n P B 1 + 0 + 1 2
cos< n, P B > =
| #?
# ? ?
√ √
= √ = = ,
n | P B 1 2 + 0 2 + ( ? 2 × 3
1) · 1 2 + 1 2 + 1 2 2 3
根据直线的方向向量与平面法向量所成角的余弦值的绝对值即为直线与平面所成角的
正弦值, √
#? # ? 6
所以直线与平面所成角的正弦值等于 | cos< n, P B > | = ,
√ 3
6
所以直线 P B 与平面 QCD 所成角的正弦值为 .
3
变式练 1.4(2020 山东 20 )
如图,四棱锥 P ? ABCD 的底面为正方形, P D ⊥ 底面 ABCD .设平面 P AD 与平面 P BC
的交线为 l .
( I ) 证明: l ⊥ 平面 P DC ;
( II ) 已知 P D = AD= 1 , Q 为 l 上的点,求 P B 与平面 QCD 所成角的正弦值的最大值.
变式练 1.4 分析 考查知识
变式练 1.4
第 58 页 共 99 页
解答 ( I ) 如图在平面 P AD 内过点 A 作 AM // P D 且 AM = P D
连接 MP ,
所以
四边形 ADP M 是平行四边形
故有 MP // AD 且 MP = AD,又因为四边形 ABCD 为
正方形,
所以有 AD// BC 且 AD= BC ,所以有 P M // BC 且
P M = BC ,
故
直线 P M 就是平面 P AD 和平面 P BC 的交线 l
因为 P D ⊥ 底面 ABCD , P D ∩ DC = D 且 AD⊥ CD ,
所以 AD⊥ 平面 P CD ,所以 l ⊥ 平面 P CD .
( II ) 以 D 为坐标原点, DA 所在直线为 x 轴, DC 所在直线为 y 轴,
DP 所在直线为 z 轴,建立如图所示的空间直角坐标系,
则
D(0 ,0 ,0) , A(1 ,0 ,0) , B (1 ,1 ,0) , C (0 ,1 ,0) , P (0 ,0 ,1) , M (1 ,0 ,1)
# ? # ? # ?
设 Q ( t, 0 ,1)( t ∈ R) ,则 DQ = ( t, 0 ,1) , DC = (0 ,1 ,0) , P B = (1 ,1 ,? 1) ;
#?
令平面
QCD 的一个法向量为
n = ( x, y, z ) ,
#? # ?
n · DC = 0 y = 0
则 所以 ,
#? # ?
n · DQ = 0 tx + z = 0
#?
令 x = 1 ,则 y = 0 , z = ? t ,即 n = (1 ,0 ,? t ) ,
设 P B 与平面 QCD 所成角为
θ ,
# ? √ …
#?
#? # ?
n · P B | t + 1 | 3
则
2 t
sinθ = cos n · P B =
| #?
# ? √ ×
= = 1 +
2
n | · P B 3 t 2 + 3 3 t + 1
要使 sin…
θ 取到最大,显然 ?
t > 0 , √
因为 2 t 2
1 +
2 = 1 + ? 2 ,当且仅当 t = 1 时等号成立,
t + 1 1
t +
t
√
6
所以 sinθ ? ,
3 √
6
故平面 QCD 与 P B 所成角的正弦值最大为 .
3
变式练 1.5(2018 江苏 25 )
如图,在正三棱柱 ABC ? A1 B 1 C 1 中, AB = AA1 = 2 ,点 P , Q 分别为 A1 B 1 , BC 的中点.
( I ) 求异面直线 BP 与 AC 1 所成角的余弦值;
( II ) 求直线 CC 1 与平面 AQC 1 所成角的正弦值.
第 59 页 共 99 页
变式练 1.5 分析 考查知识
变式练 1.5
解答 ( I ) 设 AC , A1 C 1 的中点分别为 O , O 1 ,
则 OB ⊥ OC , OO 1 ⊥ OC , OO 1 ⊥ OB ,
# ? # ? # ?
故以 {OB, OC, OO 1 } 为基底,
建立空间直角坐标系 O ? xyz , √
因为 AB = AA1 = 2 , A(0 ,? 1 ,0) , B ( 3 ,0 ,0) , C (0 ,1 ,0) ,
√
A1 (0 ,? 1 ,2) , B 1 ( 3 ,0 ,2) , C 1 (0 ,1 ,2) .
点 P 为
A√
1 B 1 的中点.
3
所以 1
P ,? ,2 ,
2√ 2
# ? 3 # ?
所以 1
BP = ? ,? ,2 , AC 1 = (0 ,2 ,2) .
2 2
# ? # ? √
# ? # ? | BP · AC | | ? 1 + 4 |
| 1 3 10
cos< BP , AC 1 > | = # ? # ? = √ √ = .
| BP | · | AC 1 | 5 × 2 2 20
√
3 10
所以异面直线 BP 与 AC 1 所成角的余弦值为: .
√
20
3
( II ) 因为 Q 为 BC 的中点.所以 1
Q , ,0 ,
√
2 2
# ? 3 # ? # ?
所以 3
AQ = , ,0 , AC 1 = (0 ,2 ,2) , CC 1 = (0 ,0 ,2) ,
2 2
设平面 AQC 1 的一个法向量为 √ ?n = ( x, y, z ) ,
# ? 3 3
AQ · ?n = x + y = 0 √
由
2 2 ,可取 ?n = ( 3 ,? 1 ,1) ,
# ?
AC 1 · ?n = 2 y + 2 z = 0
设直线 CC 1 与平面 AQC 1 所成角的正弦值为 θ ,
# ? √
# ? | CC 1 · ?n | 2 5
sinθ = | cos< CC 1 , ?n > | = # ? = √ = ,
| CC 1 | · | ?n | 5 × 2 5
√
5
所以直线 CC 1 与平面 AQC 1 所成角的正弦值为 .
5
变式练 1.6(2018 全国 I 理 18 )
如图,四边形 ABCD 为正方形, E, F 分别为 AD, BC 的中点,以 DF 为折痕把 △ DF C
折起,使点 C 到达点 P 的位置,且 P F ⊥ BF .
第 60 页 共 99 页
( I ) 证明:平面 P EF ⊥ 平面 ABF D ;
( II ) 求 DP 与平面 ABF D 所成角的正弦值.
变式练 1.6 分析 考查知识
变式练 1.6
解答 ( I ) 证明:因为 E , F 分别为 AD, BC 的中点,四边形 ABCD 为正方形
所以 EF // AB , BC ⊥ AB ;
所以
BC ⊥ EF
因为 P F ⊥ BF ,
所以 P F ⊥ BC ,
而: EF ∩ P F = F
所以 BC ⊥ 平面 P EF
而: BC ? 平面 ABF D ,
∴ 平面 P EF ⊥ 平面 ABF D .
( II ) 作 P H ⊥ EF ,垂足为 H ,由( 1 )得, P H ⊥ 平面 ABF D ,
# ?
# ?
以
H 为坐标原点, HF 的方向为 y 轴正方向, BF 为
单位长,建立如图所示的空间直角坐标系 H ? xyz ,
由( 1 )可得, DE ⊥ P E ,又 DP = 2 , DE = 1 ,
√
所以 P E = 3 ,又 P F = 1 , EF = 2 ,故 P E ⊥ P F ,
√
可得 3 3
P H = , EH =
2 √
2
3
则 3
H (0 ,0 ,0) , P 0 ,0 , , D ? 1 ,? ,0 ,
√ √ 2
2
# ? 3 3 # ? 3
DP = 1 , , , HP = 0 ,0 , 为平面 ABF D 的
2 2 2
法向量,
设 DP 与平面 ABF D 所成角为 θ ,
3
√
# ? # ?
·
4 3
则
HP DP
sinθ =
# ? √ ,
# ?
= =
HP DP 3 4 √
3
所以 DP 与平面 ABF D 所成角的正弦值为 .
4
第 61 页 共 99 页
变式练 1.7(2018 全国 III 理 19 )
? ?
如图,边长为 2 的正方形 ABCD 所在的平面与半圆弧 CD 所在平面垂直, M 是 CD 上异
于 C , D 的点.
( I ) 证明:平面 AMD ⊥ 平面 BMC ;
( II ) 当三棱锥 M ? ABC 体积最大时,求面 MAB 与面 MCD 所成二面角的正弦值.
变式练 1.7 分析 考查知识
变式练 1.7
解答 ( I ) 由题设知,平面 CMD ⊥ 平面 ABCD ,交线为 CD .
因为 BC ⊥ CD , BC ? 平面 ABCD ,
所以
BC ⊥ 平面 CMD ,故 BC ⊥ DM .
?
因为 M 为 CD 上异于 C , D 的点,且 DC 为直径,
所以
DM ⊥ CM
又 BC ∩ CM = C ,所以 DM ⊥ 平面 BMC .
而 DM ? 平面 AMD ,故平面 AMD ⊥ 平面 BMC .
?
( II ) 以 D 为坐标原点, DA 的方向为 x 轴正方向,建立如图
所示的空间直角坐标系 D? xyz .
?
当三棱锥 M ? ABC 体积最大时, M 为 CD 的中点.
由 题 设 得 D(0 ,0 ,0) , A(2 ,0 ,0) , B (2 ,2 ,0) , C (0 ,2 ,0) ,
M (0 ,1 ,1) ,
# ? # ? # ?
AM = ( ? 2 ,1 ,1) , AB = (0 ,2 ,0) , DA= (2 ,0 ,0) .
#?
设
n = ( x, y, z ) 是平面 MAB
的法向量,
#? # ?
n · AM = 0 , ? 2 x + y + z = 0 , # ?
则 即 可取 n = (1 ,0 ,2) . DA 是平面 MCD
#? # ?
n · AB = 0 . 2 y = 0 .
的法向量, √
#? # ?
#? # ? · 5
因此 n DA
cos( n, DA) =
# ?
= ,
| #?
√ n | DA 5
#? # ? 2 5
故 sin( n, DA) = ,
5 √
2 5
所以面 MAB 与面 MCD 所成二面角的正弦值是 .
5
第 62 页 共 99 页
变式练 1.8(2018 浙江 19 )
?
如图,已知多面体 ABCA 1 B 1 C 1 , A1 A, B 1 B , C 1 C 均垂直于平面 ABC , ∠ ABC = 120 , A1 A= 4 ,
C 1 C = 1 , AB = BC = B 1 B = 2 .
( I ) 证明: AB 1 ⊥ 平面 A1 B 1 C 1 ;
( II ) 求直线 AC 1 与平面 ABB 1 所成的角的正弦值.求直线 AC 1 与平面 ABB 1 所成的角的
正弦值.
变式练 1.8 分析 考查知识
变式练 1.8
解答 ( I ) 过 B 1 作 B 1 E ⊥ AA1 于点 E ,
过 C 1 作 C 1 F ⊥ BB 1 于点 F ,
B 1 E = AB = 2 , AE = BB 1 = 2 , A1 E = 2 ,
√
所以 A?
1 B 1 = A 2 2
1 E + B 1 E = 2 2 ,
√
2
AB 2
1 = BB 1 + AB = 2 2 ,
AA1 = 4 ,
2 2 2
所以 A1 B 1 + AB 1 = AA1 ,
所以 AB 1 ⊥ A1 B 1 ,
又 C 1 F = BC = 2 ,B 1 F = 1 ,
√ √
所以 B 1 C 1 = C 2 2
?
1 F + B 1 F = 5 , AC = 2 3 ,
√
2
所以 AC 1 = AC 2 + CC 1 = 13 ,
2 2 2
所以 A1 B 1 + B 1 C 1 = AC 1 ,
所以 AB 1 ⊥ B 1 C 1 ,
因为 B 1 C 1 ? 平面 A2 B 1 C 1 ,
A1 B 1 ? 平面 A1 B 1 C 1 ,
所以 AB 1 ⊥ 平面 A1 B 1 C 1 .
由题意得 BB 1 ⊥ AB , CC 1 ⊥ BC , AA1 ⊥ AB ,
所以 △ ABB 1 为直角三角形,四边形 BCC 1 B 1 为直角梯形.
√
所以 AB 1 = 2 2 , √
在 △ ?
ABC 中, AB = 2 , BC = 2 , ∠ ABC = 120 ,由余弦定理得 AC = 2 3 ,
√
在 △ ACC 1 中,由勾股定理得 AC 1 = 13 ,
第 63 页 共 99 页
√ √
同理, A1 B 1 = 2 2 在直角梯形 BCC 1 B 1 中可得 B 1 C 1 = 5 ,
2 2 2 ?
则 A1 B 1 + AB 1 = AA1 ,所以 ∠ AB 1 A1 = 90 ,
所以 AB 1 ⊥ A1 B 1 .
同理, AB 1 ⊥ B 1 C 1 .
又 A1 B 1 ∩ B 1 C 1 = B 1 ,
所以 AB 1 ⊥ 平面 A1 B 1 C 1 .
( II ) 以 A 为原点, Ax 为 x 轴, AC 为 y 轴, AA1 为 z 轴建
立空间直角坐标系, √ √
则: A(0 ,0 ,0) , A1 (0 ,0 ,4) , B (1 , 3 ,0) , B 1 (1 , 3 ,2) ,
√
C 1 (0 ,2 3 ,1) ,
# ? √
# ? √
# ?
所以 AC 1 = (0 ,2 3 ,1) , AB 1 = (1 , 3 ,2) , AA1 = (0 ,0 ,4) ,
#?
设 n = ( x, y, z ) 的法向量,
√
x + 3 y + 2 z = 0 , 4 z = 0 ,
√
#?
所以 n = ( ? 3 ,
1 ,0) ,
# ? √ √
#?
# ? #?
AC · n 2 3 39
sin AC · n =
# ? √ ,
#? = =
√ AC · | n | 2 13 13
39
所以正弦值是 .
13
如图,作 CH ⊥ AB ,垂足为 H ,
结合 CH ⊥ BB 1 知 CH ⊥ 平面 A1 ABB 1 ,
又 CC 1 // 平面 AA1 B 1 B ,
所以 CH 为 C 1 到平面 A1 ABB 1 的距离.
?
在 △ BCH 中得 ∠ CBH = 60 , BC = 2 , √ √
√
3 39
所以 CH
CH = 3 所以直线 AC 1 与平面 ABB 1 所成的角的正弦值为 = √ = .
AC 1 13 13
第 64 页 共 99 页
1.5.5 空间向量与二面角
例 1(2020 全国 I 理 18(2/5) )
如图, D 为圆锥的顶点, O 是圆锥底面的圆心, √ AE 为底面直径, AE = AD . △ ABC 是底
6
面的内接正三角形, P 为 DO 上一点, P O = DO
6
( I ) 证明 : P A ⊥ 平面 P BC
( II ) 求二面角 B ? P C ? E 的余弦值 .
D
P
C
O
E B
A
分析
考查知识
答案
解答 √ √ √
6 3 2
( I ) 设 DO = a,由题设可得 P O = a, AO = a, AB = a, P A = P B = P C = a,
6 3 2
2 2 2 2 2 2
因此 P A + P B = AB ,从而 P A ⊥ P B ,又 P A + P C = AC ;
故 P A ⊥ P C ,所以 P A ⊥ 平面 P BC .
# ? # ?
( II ) 以 O 为坐标原点, OE 的方向为 y 轴正方向, | OE | 为单
位长,建立如图所示的空间直角坐标系 O ? xyz √ .
3
由 题 设 可 得 1
E (0 ,1 ,0) , A(0 ,? 1 ,0) , C ( ? , ,0) ,
√ 2 2
2
P (0 ,0 , ) ,
2 √ √
# ? 3 # ? 2 #?
所以 1
EC = ( ? ,? ,0) , EP = (0 ,? 1 , ) ,设 m =
2 2 2
( x, y, z ) 是平面 P CE 的法向量,
则 √
?
2
#? # ? ? y + z = 0 √
m · EP = 0 √
√ 2 #? ? 3
#? # ? , ,可取 m = ,1 , 2 ;
m · EC = 0
3 1 3
? x ? y = 0
2 √
2
# ? 2 #? # ?
由( 1 )知 AP = 0 ,1 , 是平面 P CB 的一个法向量,记 n = AP ,
2 √ √
#? #?
#? #? · 2 5 2 5
则 n m
cos? n, m ? = = ,故二面角 B ? P C ? E 的余弦值为 .
| #? #?
n | · | m | 5 5
第 65 页 共 99 页
例 2(2007 福建文 17 )
如图,正三棱柱 ABC ? A1 B 1 C 1 的所有棱长都为 2 , D 为
A A1
CC 1 的中点.
( I ) 求证: AB 1 ⊥ 平面 A1 BD ;
( II ) 求二面角 A? A1 D? B 的大小(余弦值).
C C 1
D
B B 1
分析
考查知识
答案
解答
( I ) 证明:取 BC 的中点 O ,连接 AO .因为 △ ABC 为
A A1
正三角形,所以 AO ⊥ BC ;
因为正三棱柱 ABC ? A1 B 1 C 1 中,平面 ABC ⊥ 平面
BCC 1 B 1 ;
C C 1
AO ⊥ 平面 BCC 1 B 1 .连接 B 1 O ,在正方形 BB 1 C 1 C D
O
中, O , D 分别为 BC , CC 1 的中点,所以所以 B B 1
B 1 O ⊥ BD , AO ⊥ BD .
所以 BD ⊥ 平面 AOB 1 ,则 BD ⊥ AB 1 ;
ABA 1 B 1 中, AB 1 ⊥ A1 B ,所以 AB 1 ⊥ 平面 A1 BD .
# ? # ? # ?
( II ) 取 B 1 C 1 的中点 O 1 ,以 O 为原点, OB , OO 1 , OA
z
的方向为 x , y , z 轴的正方向建立空间直角坐标系; √ √ A A1
则 B (1 ,0 ,0) , D( ? 1 ,1 ,0) , A1 (0 ,2 , 3) , A(0 ,0 , 3) ,
# ?
B 1 (1 ,2 ,0) 由( 1)知 AB 1 ⊥ 平面 A1 BD ,所以 AB 1 =
√
(1 ,2 ,? 3) 为平面 A1 BD 的一个法向量. C C 1
#? # ?
设 平 面 A1 AD 的 法 向 量 为 n = ( x, y, z ) . AD= D y
√
# ? OO
? 1 ,1 ,? 3 ,AA1 = (0 ,2 ,0) . B B 1
x
√
#? # ?
n · AD= 0 , ? x + y ? 3 z = 0 , y = 0 ,
所以 所以 则 ;
√
#? # ?
n · AA1 = 0 , 2 y = 0 , x = ? 3 z
#? √
令 z = 1 得 n = ? 3 ,0 ,1 为平面 A1 AD 的一个法向量.所以 √ √ √
# ?
#? # ?
#?n · AB 1 ? 3 ? 3 6
cos n ?AB 1 =
# ?
= √ = ?
| #?
n | AB 1 2 × 2 2 4 √
6
由于二面角 A? A1 D? B 为锐角,故二面角 A? A1 D? B 的余弦值为 .
4
第 66 页 共 99 页
例 3(2020 天津 17 )
如图,在三棱柱 ABC ? A1 B 1 C 1 中, CC 1 ⊥ 平面 ABC , AC ⊥ BC , AC = BC = 2 , CC 1 = 3 ,
点 D, E 分别在棱 AA1 和棱 CC 1 上,且 AD= 1 , CE = 2 , M 为棱 A1 B 1 的中点.
( I ) 求证: C 1 M ⊥ B 1 D;
( II ) 求二面角 B ? B 1 E ? D 的正弦值;
(III) 求直线 AB 与平面 DB 1 E 所成角的正弦值.
分析
考查知识
答案
解答
# ? # ? # ?
( I ) 依题意,以 C 为原点,分别以 CA , CB , CC 1 的方向
为 x 轴, y 轴, z 轴的正方向建立空间直角坐标系(如
图),可得 C (0 ,0 ,0) , A(2 ,0 ,0) , B (0 ,2 ,0) , C 1 (0 ,0 ,3) ,
A1 (2 ,0 ,3) , B 1 (0 ,2 ,3) , D(2 ,0 ,1) , E (0 ,0 ,2) , M (1 ,1 ,3) ,
# ? # ?
C 1 M = (1 ,1 ,0) , B 1 D= (2 ,? 2 ,? 2) ,
# ? # ?
从而 C 1 M · B 1 D= 2 ? 2 + 0 = 0 ,所以 C 1 M ⊥ B 1 D.
# ? # ? # ?
( II ) 依题意, CA = (2 ,0 ,0) 是平面 BB 1 E 的一个法向量,
EB 1 = (0 ,2 ,1) , ED =
# ?
·
#? n EB 1 = 0
(2 ,0 ,? 1) ,设 n = ( x, y, z ) 为平面 DB 1 E 的法向量,则
# ?
n · ED = 0
2 y + z = 0
#?
# ? #?
即 ,不妨设 x = 1 ,可得 n = (1 ,? 1 ,2) ,因此有 cos CA ?n =
2 x ? z = 0
# ? √ √
#?
CA · n 6 # ? #? 30
# ? = ,于是 sin CA ?n = ,所以二面角 B ? B 1 E ? D 的正弦值
| #?
CA√ | | n | 6 6
30
为 .
6
# ? #?
(III) 依题意, AB = ( ? 2 ,2 ,0) ,由( 2 )知 √ n = (1 ,? 1 ,2) √为平面 DB
# ? 1 E 的一个法向量,
# ? #?
· #? 3 3
于是 AB n
cos AB ?n =
# ? ? .故正弦值为 .
#? =
AB | n | 3 3
第 67 页 共 99 页
变式练 3.1(2020 全国 III 理 19 )
如图,在长方体 ABCD ? A1 B 1 C 1 D1 中,点 E , F 分别在棱 DD1 , BB 1 上,且 2 DE = ED 1 ,
BF = 2 F B 1 .
( I ) 证明:点 C 1 在平面 AEF 内;
( II ) 若 AB = 2 , AD= 1 , AA1 = 3 ,求二面角 A? EF ? A1 的正弦值.
变式练 3.1 分析 考查知识
变式练 3.1
解答 ( I ) 在 AA1 上取一三等分点 M ,使得 A1 M = 2 AM ,分别连
接 EM , B 1 M , EC 1 , F C 1 ,
在长方体 ABCD ? A1 B 1 C 1 D1 中,有 DD1 //AA1 //BB 1 ,
且 DD1 = AA1 = BB 1 ,
又 2 DE = ED 1 , A1 M = 2 AM , BF = 2 F B 1 ,
所以 DE = AM = F B 1 ,
即
四边形 B 1 AF M 与 EDAM 都是平行四边形
所以 AF //MB 1 且 AF = MB 1 , AD= ME 且 AD//ME ,
又在长方体中,有 AD//B 1 C 1 且 AD= B 1 C 1 ,
所以
B 1 C 1 //ME 且 B 1 C 1 = ME
则
四边形 B 1 C 1 EM 为平行四边形
所以 EC 1 //MB 1 且 EC 1 = MB 1 ,
又
AF //MB 1 且 AF = MB 1
所以
AF //EC 1 且 AF = EC 1
则
四边形 AF C 1 E 为平行四边形
故点 C 1 在平面 AEF 内.
第 68 页 共 99 页
( II ) 在长方体中,以 C 1 为原点, C 1 D1 所在直线为 x 轴, C 1 B 1
所在直线为 y 轴, C 1 C 所在直线为 z 轴,建立如图所示空
间直角坐标系.因为 AB = 2 , AD= 1 , AA1 = 3 , 2 DE =
ED 1 , BF = 2 F B 1 ,所以 A(2 ,1 ,3) , E (2 ,0 ,2) , F (0 ,1 ,1) ,
A1 (2 ,1 ,0) ,
# ? # ? # ?
则 EF = ( ? 2 ,1 ,? 1) , AE = (0 ,? 1 ,? 1) , A1 E = (0 ,? 1 ,2) ,
#?
设平面
AEF 的一个法向量为
n 1 = ( x 1 , y 1 , z 1 ) ,
#? # ?
n 1 · EF = 0 ? 2 x 1 + y 1 ? z 1 = 0
则 ,即 ,
#? # ?
n 1 · AE = 0 ? y 1 ? z 1 = 0
#?
令 x 1 = 1 ,则 y 1 = 1 , z 1 = ? 1 ,即 n 1 = (1 ,1 ,? 1) .
#?
设平面
A1 EF 的一个法向量为
n 2 = ( x 2 , y 2 , z 2 ) ,
#? # ?
n 2 · EF = 0 ? 2 x 2 + y 2 ? z 2 = 0
#?
则 ,即 ,令 x = 1 ,则 y = 4 , z = 2 ,即 n =
2 2 2 2
#? # ?
n 2 · A1 E = 0 ? y 2 + 2 z 2 = 0
(1 ,4 ,2) ,
所以 #? #? √
#? #? n 1 · n 2 1 + 4 ? 2 7
cos? n 1 · n 2 ? = | #? #? = √ √ =
n 1 | · | n 2 | 3 · 21 7
设二面角 A? EF ? A1 为 θ ,则 …
√
1 42
sinθ = 1 ? =
7 7 √
即 42
二面角 A? EF ? A1 的正弦值为 7
变式练 3.2(2020 江苏理 24 ) √
在三棱锥 A? BCD 中,已知 CB = CD = 5 , BD = 2 , O 为 BD 的中点, AO ⊥ 平面 BCD ,
AO = 2 , E 为 AC 的中点.
( I ) 求直线 AB 与 DE 所成角的余弦值;
1
( II ) 若点 F 在 BC 上,满足 BF = BC ,设二面角 F ? DE ? C 的大小为 θ ,求 sinθ 的
4
值.
变式练 3.2 分析 考查知识
第 69 页 共 99 页
变式练 3.2
解答 ( I ) 连结 OC ,
因为 CB = CD , O 为 BD 中点,
所以 CO ⊥ BD ,又 AO ⊥ 平面 BCD ,
所以 AO ⊥ OB , AO ⊥ OC .
# ? # ? # ?
以 OB, OC, OA 为基底,建立空间直角坐标系 O ?
xyz . √
因为 BD = 2 , CB = CD = 5 , AO = 2 ,
所以 B (1 ,0 ,0) , D( ? 1 ,0 ,0) , C (0 ,2 ,0) , A(0 ,0 ,2) .
则
# ? # ?
AB = (1 ,0 ,? 2) , DE = (1 ,1 ,1)
所以 # ? # ? √
# ? # ? | AB · DE | | 1 + 0 ? 2 |
| cos? 15
AB, DE ?| = # ? # ? = √ √ =
| AB | · | DE√ | 5 × 3 15
15
因此,直线 AB 与 DE 所成角的余弦值为 .
15
1 # ?
( II ) 因为点 F 在 BC 上, BF = BC , BC = ( ? 1 ,2 ,0) ,
4
所以
# ? 1 # ? 1 1
BF = BC = ? , ,0
# ? 4 4 2
又 DB = (2 ,0 ,0) ,故
# ? # ? # ? 7 1
DF = DB + BF = , ,0
4 2
#?
设 n 1 = ( x 1 , y 1 , z 1 ) 为平面 DEF 的一个法向量,
# ? #?
DE · n 1 = 0 x 1 + y 1 + z 1 = 0
#?
则
# ? ,即 取 x 1 = 2 ,得 y 1 = ? 7 , z 1 = 5 ,所以 n 1 =
#?
7 1
DF · n 1 = 0 x 1 + y 1 = 0
4 2
(2 ,? 7 ,5) .
#? # ?
设
n 2 = ( x 2 , y 2 , z 2 ) 为平面
DEC 的一个法向量,又 DC = (1 ,2 ,0) ,
# ? #?
DE · n 2 = 0 x 2 + y 2 + z 2 = 0
则
# ? ,即 ,取 x 2 = 2 ,得 y 2 = ? 1 ,得 z 2 = ? 1 ,所以
#?
DC · n 2 = 0 x 2 + 2 y 2 = 0
#?
n 2 = (2 ,? 1 ,? 1) .
故 | #? #? √
n · n | | 4 + 7 ? 5 |
| 1 2
cosθ | 13
= = √ √ =
| #? #?
√ n 1 | · | n 2 | 78 × 6 13
√
2 39
所以 sinθ = 1 ? cos2 θ = .
13
变式练 3.3(2019 全国 III 理 19 )
图 1 是由矩形 ADEB , Rt△ ABC 和菱形 BF GC 组成的一个平面图形,其中 AB = 1 , BE =
?
BF = 2 , ∠ F BC = 60 .将其沿 AB , BC 折起使得 BE 与 BF 重合,连结 DG ,如图 2 .
( I ) 证明:图 2 中的 A, C , G , D 四点共面,且平面 ABC ⊥ 平面 BCGE ;
第 70 页 共 99 页
( II ) 求图 2 中的二面角 B ? CG ? A 的大小.
变式练 3.3 分析 考查知识
变式练 3.3
解答 ( I ) 由已知得 AD// BE , CG // BE ,
所以
AD// CG ,故 AD, CG 确定一个平面
从而 A, C , G , D 四点共面.
由已知得
AB ⊥ BE , AB ⊥ BC
故
AB ⊥ 平面 BCGE
又因为 AB ? 平面 ABC ,
所以
平面 ABC ⊥ 平面 BCGE
( II ) 作 EH ⊥ BC ,垂足为 H .
因为 EH ? 平面 BCGE ,平面 BCGE ⊥ 平面 ABC ,
所以
EH ⊥ 平面 ABC
?
由已知,菱形 BCGE 的边长为 2 , ∠ EBC = 60 ,
可求得 √
BH = 1 , EH = 3
# ?
以 H 为坐标原点, HC 的方向为 x 轴的正方向,
建立如图所示的空间直角坐标系 H √ ? xyz ,
# ? √
# ?
则 A( ? 1 ,1 ,0) , C (1 ,0 ,0) , G (2 ,0 , 3) , CG = (1 ,0 , 3) , AC = (2 ,? 1 ,0) .
#?
设平面
ACGD 的法向量为
n = ( x, y, z ) ,
√
# ? #?
CG · n = 0 x + 3 z = 0 √
#?
则 ?
# ? ,即 .所以可取 n = (3 ,6 , 3) .
#?
AC · n = 0 2 x ? y = 0
#?
又平面 BCGE 的法向量可取为 m = (0 ,1 ,0) ; √
所以 #? #?
#? #? n · m 3
cos? n, m ? = =
| #? #?
n || m | 2
因此
二面角 B ? CG ? ?
A 的大小为 30
第 71 页 共 99 页
变式练 3.4(2019 全国 II 理 17 )
如图,长方体 ABCD ? A1 B 1 C 1 D1 的底面 ABCD 是正方形,点 E 在棱 AA1 上, BE ⊥ EC 1 .
( I ) 证明: BE ⊥ 平面 EB 1 C 1 ;
( II ) 若 AE = A1 E ,求二面角 B ? EC ? C 1 的正弦值.
变式练 3.4 分析 考查知识
变式练 3.4
解答 ( I ) 由已知得 B 1 C 1 ⊥ 平面 ABB 1 A1 , BE ? 平面 ABB 1 A1 ,
故
B 1 C 1 ⊥ BE
又
BE ⊥ EC 1
所以
BE ⊥ 平面 EB 1 C 1
?
( II ) 由 I 知 ∠ BEB 1 = 90 .
? ?
由题设知 Rt △ ABE = Rt △ A1 B 1 E ,所以 ∠ AEB = 45 ,
故
AE = AB , AA1 = 2 AB
# ? # ?
以 D 为坐标原点, DA 的方向为 x 轴正方向, | DA| 为
单位长,建立如图所示的空间直角坐标系 D? xyz ,
# ?
则 C (0 ,1 ,0) , B (1 ,1 ,0) , C 1 (0 ,1 ,2) , E (1 ,0 ,1) , CE =
# ?
(1 ,? 1 ,1) , CC 1 = (0 ,0 ,2) .
#?
设平面 EBC 的法向量为 n = ( x 1 , y 1 , z 1 ) ,
?
# ? ?
#?
CB · n = 0 , x 1 = 0 ,
#?
则 # ? #? 即 所以可取 n = (0 ,? 1 ,? 1) .
CE · n = 0 , x 1 ? y 1 + z 1 = 0 ,
#?
设平面 ECC 1 的法向量为 m = ( x
?
2 , y 2 , z 2 ) ,
# ? ?
#?
CC 1 · m = 0 , 2 z 2 = 0 ,
#?
则 # ? #? 即 所以可取 m = (1 ,1 ,0) .
CE · m = 0 , x 2 ? y 2 + z 2 = 0 .
#? #?
#? #? ·
于是 n m 1
cos< n, m > = | #? #? = ? .
n | · | m | 2 √
3
所以,二面角 B ? EC ? C 1 的正弦值为 .
2
第 72 页 共 99 页
变式练 3.5(2019 天津理 17 )
如图, AE ⊥ 平面 ABCD , CF // AE , AD// BC , AD⊥ AB , AB = AD= 1 , AE = BC = 2 .
( I ) 求证: BF // 平面 ADE ;
( II ) 求直线 CE 与平面 BDE 所成角的正弦值;
(III) 若二面角 E ? 1
BDF 的余弦值为 ,求线段 CF 的长.
3
变式练 3.5 分析 考查知识
变式练 3.5
# ? # ? # ?
解答 ( I ) 依题意,可以建立以 A 为原点,分别以 AB , AD, AE
的方向为 x 轴, y 轴, z 轴正方向的空间直角坐标系(如
图),
可得 A(0 ,0 ,0) , B (1 ,0 ,0) , C (1 ,2 ,0) , D(0 ,1 ,0) , E (0 ,0 ,2) .
设 CF = h ( h > 0) ,则 F (1 ,2 , h ) .
# ? # ?
依题意, AB = (1 ,0 ,0) 是平面 ADE 的法向量,又 BF =
# ? # ?
(0 ,2 , h ) ,可得 BF · AB = 0 ,
又因为直线 BF ?? 平面 ADE ,所以 BF // 平面 ADE .
# ? # ? # ?
( II ) 依题意, BD = ( ? 1 ,1 ,0) , BE = ( ? 1 ,0 ,2) , CE = ( ? 1 ?
2 ,2) ,
#? # ?
·
?
#? n BD = 0 x + y = 0
设 n = ( x, y, z ) 为平面 BDE 的法向量,则 ,即 ,
#? # ?
n · BE = 0 ? x + 2 z = 0
# ?
#?
# ? #?
#? | CE · n |
不妨令 4
z = 1 ,可得 n = (2 ,2 ,1) ,因此有 | cos CE, n | = # ? = .
| #?
CE | · | n | 9
故直线 4
CE 与平面 BDE 所成角的正弦值为 .
9
#?
(III) 设
m = ( x, y, z ) 为平面
BDF 的法向量,
#? # ?
m · BD = 0 ? x + y = 0
#?
则 ,即 ,不妨令 2
y = 1 ,可得 m = 1 ,1 ,? ,
#? # ?
h
m · BF = 0 2 y + hz = 0
2
#? #?
4 ?
m · n h
由题意,有 | #? #? 1
cos? m, n ?| = = ?
= ,
| #? #?
m || n | 4 3
3 2 +
2
h
解得 8 8
h = ,经检验,符合题意.所以,线段 CF 的长为 .
7 7
第 73 页 共 99 页
变式练 3.6(2019 全国 I 理 18 )
如图,直四棱柱 ABCD ? ?
A1 B 1 C 1 D1 的底面是菱形, AA1 = 4 , AB = 2 , ∠ BAD = 60 , E , M ,
N 分别是 BC , BB 1 , A1 D 的中点.
( I ) 证明: MN // 平面 C 1 DE ;
( II ) 求二面角 A? MA 1 ? N 的正弦值.
变式练 3.6 分析 考查知识
变式练 3.6
解答 ( I ) 连结 B 1 C, ME ,因为 M , E 分别为 BB 1 , BC 的中点,
所以 1
ME // B 1 C ,且 ME = B 1 C .
2
又因为 N 为 A1 D 的中点,
所以 1
ND = A1 D.
2
由题设知 A1 B 1 // DC 且 A1 B 1 = DC ,
可得 B 1 C // A1 D 且 B 1 C = A1 D,
故 ME // ND 且 ME = ND ,因此四边形 MNDE 为平
行四边形, MN // ED .
又 MN ?? 平面 C 1 DE ,所以 MN // 平面 C 1 DE .
# ?
( II ) 由已知可得 DE ⊥ DA.以 D 为坐标原点, DA 的方向为
x 轴正方向,建立如图所示的空间直角坐标系 D? xyz ,
则 √
# ?
A(2 ,0 ,0) , A1 (2 ,0 ,4) , M 1 , 3 ,2 , N (1 ,0 ,2) , A1 A=
# ? √
# ?
(0 ,0 ,? 4) , A1 M = ? 1 , 3 ,? 2 , A1 N = ( ? 1 ,0 ,? 2) ,
# ? √
MN = 0 ,? 3 ,0 .
#?
设
m = ( x, y, z ) 为 平 面 A1 MA 的 法 向 量, 则
#? # ?
m · A1 M = 0 ?
#? # ?
m · A1 A= 0 .
√
? x + 3 y ? 2 z = 0 ? √
#?
所以 可取 m = 3 ,1 ,0 .
? 4 z = 0 .
#?
设 n = ( p, q, r ) 为平面 A1 MN 的法向量,
第 74 页 共 99 页
#? # ?
n · MN = 0 ? √
?
# ? 3 q = 0 ?
#?
则
#?n · ?
A .所以
1 N = 0 . ,可取 n = (2 ,0 ,
1.2 共面问题 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
1.3 平行问题 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
1.3.1 平行之点共面 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16
1.3.2 平行问题基础理论 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
1.3.3 正向平移证平行问题 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
1.3.4 平行的传递性 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
1.3.5 反向沿线找点找线平移法 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
1.4 垂直问题 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24
1.4.1 垂直问题基础理论 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24
1.4.2 垂直问题基础理论 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
1.4.3 系统法 1:面 ⊥ 面 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26
1.4.4 系统法 2:二线 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28
1.4.5 系统法 3:三勾股 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30
1.4.6 系统法 4:四图一柱 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33
1.4.7 系统法 5:五射影 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 38
1.4.8 系统法 6:转化 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39
1.4.9 平行垂直综合 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40
1.5 立体几何与空间向量 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 49
1.5.1 空间向量与线线角 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 50
1.5.2 空间向量与点到面的距离 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 51
1.5.3 定义法与角度问题 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 52
1.5.4 空间向量与线面角 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 54
1.5.5 空间向量与二面角 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 65
1.5.6 空间向量与动点设点 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 79
1.6 文科专项 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 82
1.6.1 直接法求体积 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 82
1.6.2 平行换点求体积 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 84
1.6.3 等分点求体积 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 86
1.6.4 割补法求体积 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 88
1.6.5 表面积和面积问题 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 90
1.6.6 直接法求点到面的距离 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 93
1.6.7 平行换点求点到面的距离 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 96
1.6.8 等体积法求点到面的距离 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 97
第 1 页 共 99 页
第 1 章 立体几何之外接球
1.1 立体几何之外接球
总结:? ?
球心在过两个不平行平面的外接圆圆心
球心
且分别垂直于两个平面的两条直线的交点
长方体模型
柱体模型 正方体模型
三条棱 a、 b 、 c 两两相互垂直
?
对棱相等模型 1
柱切锥(柱体的切割体)模型
核
对棱相等模型 2
心
正棱锥模型
模
锥体模型 侧棱垂直底面模型
四个模型
型
球心的投影在面的外接圆圆心上模型
?
θ =90
全等三角形折叠模型
等腰三角形底边与直角
面 α 面 β 夹角 θ 模型
三角形斜边构成二面角
的四面体
θ 为任意角
外接球之柱体模型
柱体模型:?
、 、 长方体的长宽高
a b c
√
长方体模型 2 2 2
a + b + c
R =
2
a 正方体的棱 √
柱体模型 正方体模型
2 2 2
a + a + a
R =
2
、 、 相互垂直的三条边
a b c
√
a、 b 、 c 相互垂直的三条边 a2 + b 2 + c 2
R = 2
例 1(柱体模型 )
√
a2 + b 2 + c 2
证明 R = ;
2
分析
考查知识
答案
解答 √
a2 + b 2 + c 2
由此模型可知球心在体对角线的中点,所以 R = 2
第 3 页 共 99 页
对棱相等
总结:?
α, β, γ 为对棱长,且在长方体对角线上
对棱相等模型 1 2 2 2
1 α + β + γ
R =
2 2
α 、 α 、 α 为对棱长,且在正方体对角线上
对棱相等
2 2 2
1 α + α + α
本质为正四面体
对棱相等模型 R = , :
2
2 2
√
6 R 外接球 3
它的高 h = α ? =
3 R 内切球 1
例 2(对棱相等 )
证明
2 2 2
1 α + β + γ
R =
2 2
分析
考查知识
答案
解答
第一步:画出一个长方体或正方体,标出三组互为异面直线的对棱;第二步:设出长方
体的长宽高分别为 a, b , c , AD=BC =α , AB =CD =β , AC =DD=γ .
2 2 2
a + b = α
列方程组得 2 2 2
b + c = β
2 2 2
b + c = γ
2 2 2 2 2 2
第三步:根据柱体模型和第二步得 : 2(a + a + a ) =α + β + γ
2 2 2
1 α + β + γ
第四步: R =
2 2
第 4 页 共 99 页
外接球之锥体模型
总结:?
为侧棱、 为高
b h
2
正棱锥模型 b
R =
2 h
h 侧棱长, r 为底面多边形的外接圆半径
直棱柱与直圆柱也满足此公式
锥体模型 侧棱垂直底面模型
2
h
2
R = + r
4
h 为球心到平面的距离
球心的投影在面的外接圆圆心上模型
r 为面的外接圆半径
√
R = h 2 + r 2
锥体之正棱锥模型:?
b 为侧棱、 h 为高
锥体之正棱锥模型 2
b
R =
2 h
例 3(正棱锥模型 )
2
b
证明 R =
2 h
分析
考查知识
第 5 页 共 99 页
答案
解答 由题意可知:在正棱锥 A? BCD 中, O 为球心, OA , O , OC , OD 为半径;
令 O 1 为 △ BCD 的外接圆圆心,令其半径 O 1 D 为 r ,令正棱锥的高 AO 1 为 h 令侧棱长
AD=b ;
在直角 △ DOO 1 中
2 2 2 2 2 2 2 2 2 2 2
OD = R = | OO 1 | + | DO 1 | = ( h ? R ) + r = h + r ? 2 Rh + R = b ? 2 Rh + R
2
所以 R =2 Rh , 即 2
b
R =
2 h
第 6 页 共 99 页
侧棱垂直底面或直棱柱与直圆柱模型
总结:?
h 侧棱长, r 为底面多边形的外接圆半径
直棱柱与直圆柱也满足此公式
侧棱垂直底面模型
2
h
R = + r 2
4
例 4(侧棱垂直底面模型 )
分析
考查知识
答案
解答
如第一个图,(其他证明类似) OD =R , O 1 D 为 △ ABC 的外接圆半径;
令 O 1 D= r 所以 a b c
2 r = = =
sinA sinB sinC
在 △ P AD 中,令 P A =l ,由中位线定理可知
P A h
OO 1 = =
2 2
在 △ OO 1 D 中,由勾股定理得 …
2
h
OO 1 = R = + r 2
4
第 7 页 共 99 页
球心的投影在面的外接圆圆心上模型
球心的投影在面的外接圆圆心上模型:?
h 为球心到平面的距离
球心的投影在面的外接圆圆心上模型 为面的外接圆半径
r
√
R = h 2 + r 2
例 5(球心的投影在面的外接圆圆心上模型 )
【球心的投影在面的外接圆圆心上模型图】
分析
考查知识
答案
解答
如第一个图, OC =R ,令 OO 1 =h , O 1 C = r 为 △ ABC 的外接圆半径,在 △ OO 1 C 中,
由勾股定理得 √
R= h 2 + r 2
通常利用勾股定理求解
2 2 2
R = | R ? | P O 1 || + | O 1 C |
第 8 页 共 99 页
外接球之平面 α 平面 β 夹角 θ 模型
总结:?
为 的外接圆半径
r 1 α
? r 2 为 β 的外接圆半径 l 为 α 与 β 交线
θ =90
2
l
2 2 ?
R = r + r
1 2
4
全等三角形或者等腰拼在一起
或者菱形折叠折叠的二面角为 θ
h 为一个面的顶点到两面交线中点的距离
全等三角形折叠
r 同一个面的外接圆半径
平
θ
2 ? 2 2
面
R = r + ( h r ) tan
2
α
等腰三角形底边与直角
平
三角形斜边构成二面角为 θ
面
h 等腰三角形底边的高
等腰与直角三角形
β
等腰三角形外接圆半径
r
夹
2
?
( h r )
2
角
R = r +
2
sin θ
θ
两个等腰三角形(不全部等)公底边
模
的二面角 等腰三角形底边
θ ?
型
剖面图一致
与直角三角形直角边共边二面角 θ
θ
2
2
R = r + ( h ? r ) 2 tan
2
l 为 α 与 β 交线
θ 为面 α 与面 β 的夹角
m 为 α 的外接圆圆心到 l 中点的距离
θ = 任意角
为 的外接圆圆心到 中点的距离
n β l
2 2 2
2 m + n ? 2 mncosθ l
R =
2 +
sin θ 4
总结:?
r 1 为 α 的外接圆半径 r 2 为
β 的外接圆半径
?
θ =90 2
l
l 为 α 与 β 交线: R = r 2 2
1 + r 2 ?
4
第 9 页 共 99 页
例 6( )
?
【面 α 面 β 夹角 θ =90 模型图】
分析
考查知识
答案
解答
由题意可知:平面 ABC ⊥ BCD , O 为球心, BC =l , E 为 BC 的中点,如第二个图为
例证明:(其他证明类似), OC =R ,令 O 1 一定是 △ BCD 的外接圆半径,令其为 r 1 ,
令 O 2 一定是 △ ABC 的外接圆半径,令其为 r 2 所以四边形 EO 1 OO 2 为矩形,
2 2 2 2 2 2
R =| OD | =| OO 1 | +| O 1 D| =| O 2 E | +| O 1 D|
2
1 l
=(| 2
O 2 C | -| 2 2 2 2 2 2 2
CE | )+| O 1 D| =| O 2 C | -( | BC | ) +| O 1 D| =r 1 + r 2 ?
2 4
2
l
所以 R = r 2 2
1 + r 2 ?
4
第 10 页 共 99 页
总结:?
全等三角形或者等腰拼在一起
或者菱形折叠折叠的二面角为 θ
h 为一个面的顶点到两面交线
全等三角形折叠
中点的距离
r 同一个面的外接圆半径
2 θ
R = r 2 + ( h ? r ) 2 tan
2
题型 2 全等三角形折叠
例 7( )
【全等三角形折叠模型图】
分析
考查知识
答案
解答
题设:两个全等的三角形或者等腰拼在一起,或者菱形折叠,设折叠的二面角
∠ ′ ′ ′
AEC =θ , CE =AE =h , H 1 和 H 2 分别为 △ BCD 和 △ ABD 的外接圆
BD θ
圆 心, 在 △ ′
OEC 中, CH =r = , EH 1 =h ? r , OH 1 =( h ? r ) tan ,
2 sin△ BCD
2
2 2 2 2 2 2 2 θ
2 θ
R =| OC | =| OH 1 | +| CH 1 | =r + ( h ? r ) tan 所以: R = r 2 + ( h ? r ) 2 tan
2 2
第 11 页 共 99 页
总结:?
等腰三角形底边与直角三角形斜边构成二面角为 θ
h 等腰三角形底边的高 r 等腰三角形外接圆半径
等腰底边与直角斜边
2
?
( h 2 r 2 )
R = r 2
1 +
2
sin θ
题型 3 等腰三角形底边与直角三角形斜边构成二面角的四面体
例 8( )
【等腰三角形与直角三角形斜边构成二面角的四面体】
分析
考查知识
答案
解答
凡是遇到直角三角形,通常要转换直角顶点,因为直径所对的圆周角为直角,故可将
直角顶点转换为共斜边的直角三角形直角顶点,如上图: △ ABC 以斜边 BC 为交线
与其它平面形成的二面角可以转换为平面 DBC 与其它平面构成的二面角.如上图中,
△ ABC 为等腰三角形,且 AB = AC , △ DBC 是以 BC 为斜边的 Rt △ ,二面角为 θ ,
令: △ ABC 的外接圆半径为 r 2 ,边上的高为 AO 1 =h 2 , BC =2 r 1 , F 为, △ ABC 的外心,
2 2
( h 2 ? r 2 ) ( h 2 ? r 2 )
在 △ 2 2 2 2 2
OO 1 E 中, R =| OE | =| OO 1 | +| O 1 E | =r 1 +
2 所以: R = r 2
1 +
2
sin θ sin θ
第 12 页 共 99 页
含二面角 θ 的外接球终结公式:
?
l 为 α 与 β 交线
θ 为面 α 与面 β 的夹角
为 的外接圆圆心到 中点的距离
含二面角 m α l
θ 的外接球终结公式
n 为 β 的外接圆圆心到 l 中点的距离
2 2 2
?
2 m + n 2 mncosθ l
R =
2 +
sin θ 4
例 9( )
【含二面角 θ 的外接球终结公式模型图】
分析
考查知识
答案
解答
如图,若空间四边形 C ? ABD 中,二面角的平面角大小为 θ , ABD 的外接圆圆心
为 O 1 , ABC 的外接圆圆心为 O 2 , E 为公共弦 AB 中点,则 ∠ O 1 EO 2 =θ , O 1 E =m ,
1 O 1 O 2
O 2 E =n , AE = l ,由于 O 、 O 1 、 E 、 O 2 四点共圆,且 OE =2R 1 = 根据余弦定理
2 sinθ
| 2 2 2
O 1 O 2 | =m + n ? 2 mn cosθ ,
2 2 ? 2
2 2 2 m + n 2 mncosθ l
R =| OE | +| AE | =
2 +
sin θ 4
第 13 页 共 99 页
1.2 共面问题
例 1(2020 全国 III 理 19 )
如图,在长方体 ABCD ? A1 B 1 C 1 D1 中,点 E , F 分别在棱 DD1 , BB 1 上,且 2 DE = ED 1 ,
BF = 2 F B 1 .
( I ) 证明:点 C 1 在平面 AEF 内;
分析
考查知识
答案
解答
( I ) 在 AA1 上取一三等分点 M ,使得 A1 M = 2 AM ,分
别连接 EM , B 1 M , EC 1 , F C 1 ,
在 长 方 体 ABCD ? A1 B 1 C 1 D1 中, 有
DD1 //AA1 //BB 1 ,且 DD1 = AA1 = BB 1 ,
又 2 DE = ED 1 , A1 M = 2 AM , BF = 2 F B 1 ,
所以 DE = AM = F B 1 ,即
四边形 B 1 AF M 与 EDAM 都是平行四边形
所以 AF //MB 1 且 AF = MB 1 , AD= ME 且 AD//ME ,
又在长方体中,有 AD//B 1 C 1 且 AD= B 1 C 1 ,
所以
B 1 C 1 //ME 且 B 1 C 1 = ME
则 四边形 B 1 C 1 EM 为平行四边形,
所以 EC 1 //MB 1 且 EC 1 = MB 1 ,
又
AF //MB 1 且 AF = MB 1
所以
AF //EC 1 且 AF = EC 1
则 四边形 AF C 1 E 为平行四边形,
故点 C 1 在平面 AEF 内.
第 14 页 共 99 页
1.3 平行问题
第 15 页 共 99 页
1.3.1 平行之点共面
例 1(2020 全国 III 文 19 )
如图,在长方体 ABCD ? A1 B 1 C 1 D1 中,点 E , F 分别在棱 DD1 , BB 1 上,且 2 DE = ED 1 ,
BF = 2 F B 1 .证明:
( I ) 当 AB = BC 时, EF ⊥ AC ;
( II ) 点 C 1 在平面 AEF 内.
分析
考查知识
答案
解答 ( I ) 当 AB = BC 时, EF ⊥ AC .
因为 ABCD ? A1 B 1 C 1 D1 是长方体,
所以
BB 1 ⊥ 平面 ABCD
又 AC ? 平面 ABCD ,所以
AC ⊥ BB 1
又因为 AB = BC ,所以四边形 ABCD 为正方形,
故有
AC ⊥ BD
又 BD ∩ BB 1 = B ,
所以
AC ⊥ 平面 BB 1 D1 D
又因为点 E , F 分别在棱 DD1 , BB 1 上,即 EF ? 平面 BB 1 D1 D,所以 EF ⊥ AC .
( II ) 取 AA1 靠近 A1 的三等分点 M ,连结 D1 M , C 1 F , MF ,
因为 E 在 DD1 ,且 2 DE = ED 1 ,
所以
ED 1 //AM ,且 AM = ED 1
所以四边形 AED 1 M 为平行四边形,
即有
D1 M //AE ,且 D1 M = AE
又 F 在 BB 1 上,且 BF = 2 F B 1 ,
所以 MF //A1 B 1 ,且 MF = A1 B 1 ,
故
第 16 页 共 99 页
MF //D1 C 1 , MF = D1 C 1 ,即 D1 MF C 1 为平行四边形
所以
D1 M //C 1 F , AE //C 1 F
故 A, E , F , C 1 四点共面,所以 C 1 在平面 AEF 内.
第 17 页 共 99 页
1.3.2 平行问题基础理论
平行问题基础理论: ?
1.3.3 正向平移证平行问题
总结:?
说明 :以线 (已知直线 ) 平行与面 (已知平面 ) 为核心
把已知直线沿某条直线平移到已知平面内
如何
第 一 招 :
让线过顶点或特殊点 线不超过面的轮廓
平移
正向沿线 与面的交点为点,与相应点的连线为线
找点找线
(一长一短 : 中位线定理 (相似 )
平移法
如何 一样长:平行四边形
证明
证明平行四边形常用的方法 : 一组对边平行且相等
两组对边分别平行 两组对边分别相等
第 18 页 共 99 页
1.3.4 平行的传递性
例 1(2020 北京 16 )
如图,在正方体 ABCD ? A1 B 1 C 1 D1 中, E 为 BB 1 中点.
( I ) 求证: BC 1 // 平面 AD1 E .
分析
考查知识
答案
解答
//
( I ) 在正方体 ABCD ? A1 B 1 C 1 D1 中, AB = C 1 D1 ,
所以
四边形 ABC 1 D1 为平行四边形,则 AD1 // BC 1
又因为 BC 1 ∈/ 平面 AD1 E , AD1 ? 平面 AD1 E ,
所以
BC 1 // 平面 AD1 E
例 2(2010 浙江 )
?
如图,在平行四边形 ABCD 中, AB = 2 BC , ∠ ABC = 120 . E
为线段 AB 的中点,将 △ ADE 沿直线 DE 翻折成 △ A1 DE ,
使平面 A1 DE ⊥ 平面 BCD , F 为线段 A1 C 的中点.
( I ) 求证: BF // 平面 A1 DE ;
分析
考查知识
答案
第 19 页 共 99 页
解答
证明:正向沿线找点找线平移法找到点 G ;
取 A1 D 的中点 G ,连结 GF , CE ;
由条件易知 1
F G // CD , F G = CD
2
又 1
BE // CD , BE = CD
2
所以
F G // BE , F G = BE
故四边形 BEGF 为平行四边形,所以
BF // EG
因为 EG ? 平面 A1 DE , BF ?? 平面 A1 DE ,所以 BF
平面 A1 DE
变式练 2.1(2017 全国 II 理 19 )
如图,四棱锥 P ? ABCD 中,侧面 P AD 为等边三角形且垂直于底面三角形 BCD , AB =
1 ?
BC = AD, ∠ BAD = ∠ ABC = 90 , E 是 P D 的中点.
2
( I ) 证明:直线 CE // 平面 P AB ;
变式练 2.1 分析 考查知识
变式练 2.1
解答 ( I ) 取 P A 中点 F ,连接 BF , EF ,
因为 E , F 分别为 P D , P A 中点,
所以 1
EF // AD
2
?
因为 ∠ BAD = ∠ ABC = 90 ,所以 BC //AD,
所以 1
BC // AD
2
所以
BC //EF
所以四边形 BCEF 为平行四边形,
第 20 页 共 99 页
所以
CE //BF
因为 BF ? 平面 P AB , CE ?? 平面 P AB ,
所以 CE // 平面 P AB .
例 3(2017 全国 I )
?
如图,在四棱锥 P ? ABCD 中, AB // CD ,且 ∠ BAP = ∠ CDP = 90 .
( I ) 证明:平面 P AB ⊥ 平面 P AD ;
分析
考查知识
答案
?
解答 ( I ) 因为 ∠ BAP = ∠ CDP = 90 ,
所以
P A ⊥ AB , P D ⊥ DC
又因为 AB // DC ,
所以
AB ⊥ P D
又因为 P A ∩ P D = P ,
所以 AB ⊥ 平面 P AD ,因为 AB ? 平面 P AB ,
所以
平面 P AB ⊥ 平面 P AD .
第 21 页 共 99 页
1.3.5 反向沿线找点找线平移法
总结:?
说明 :以线 (已知直线 ) 平行与面 (已知平面 ) 为核心
把己知平面上的线沿某条直线平移到已知直线
如何
构建此时相交直线所形成的面
第 二 招 :
平移
证明两个平面平行即可
反向沿线
一长一短 中位线定理 相似
( : ( )
找点找线
一样长:平行四边形
平移法
如何
证明平行四边形常用的方法
证明
一组对边平行且相等 两组对边分别平行
两组对边分别相等
例 1(2013 辽宁 )
如图, AB 是圆 O 的直径, P A 垂直圆 O 所在的平面, C 是
圆 O 上的点.
( I ) 设 Q 为 P A 的中点, G 为 ?AOC 的重心,求证: QG //
平面 P BC .
分析
考查知识
答案
第 22 页 共 99 页
解答
证明:反向平移 P C 找到点 M ;即取 AC 的中点为 M ,
连接 QM , OM , QO .由 G 为 ?AOC 的重心,得 M
为 AC 中点,由 G 为 P A 中点,得
QM // P C
又 O 为 AB 中点,得
OM // BC
因为 QM ∩ MO =M , QM ? 平面 QMO .
所以 QG // 平面 P BC .
变式练 1.1(2018 天津理 17 )
如图, AD// BC 且 AD= 2 BC , AD⊥ CD , EG // AD 且 EG = AD, CD // F G 且 CD = 2 F G ,
DG ⊥ 平面 ABCD , DA= DC = DG = 2 .
( I ) 若 M 为 CF 的中点, N 为 EG 的中点,求证: MN // 平面 CDE ;
变式练 1.1 分析 考查知识
变式练 1.1
解答 ( I ) 取 GD 的中点为 O ,
第 23 页 共 99 页
1.4 垂直问题
1.4.1 垂直问题基础理论
垂直问题基础理论:? 立体几何证明问题中的转化思想
? 直线与平面垂直的定义:如果直线 l 与平面 α 内的任意一条直线都垂直,我们就说直线 l
与平面 α 相互垂直,记作 l ⊥ α .
? 直线与平面垂直的判定与性质 :
判定定理:如果一条直线与一个平面内的两条相交直线都
垂直,那么该直线与此平面垂直 . (简记为“线线垂直 ?
线面垂直”)
a?
α
b ? α
符号语言: l ⊥ a ?l ⊥ α
l ⊥ b
a∩ b = O
性质定理:垂直于同一平面的两条直线平行;一条直线垂
直于一个平面,则这条线垂直于平面内的所有直线
符号语言: ? ?
a⊥ α a⊥ α
?a⊥ b ; ?a⊥ ? ( 任意 m, n, b ) .
b ⊥ α ? ( 任意) m, n, b ? α
? 直线与平面所成的角
平面的一条斜线和它在平重上的投影所成的锐角,叫做这
条直线和这个平面所成的角 .
注:
1. 一条直线垂直于平面,该直线与平面所成的角为直角;
2. 一条直线与平面平行或在平面内,则此直线与平面所成
?
的角是 0 的角;
3. 直线与平面所成角的范围是 π
[0, ].
2
第 24 页 共 99 页
1.4.2 垂直问题基础理论
总结:? 平面与平面垂直的判定与性质 :
1. 二面角:从一条直线出发的两个半平面所组成的图形叫
做二面角 .
2. 二面角的平面角:在二重角的棱上任取一点,以该点为
垂足,在二面角的两个半平面内分别作垂直于棱的两条射
线,这两条射 ∠ AOB 即为二面角 α ? l ? β 的平面角 .
3. 二重角的平面角的范围是 [0 , π ].
? 平面与平面垂直的定义 : 一般地,两个平面相交,如果它们所成的二面角是直二面角,就
说这两个平面互相垂直 . 面面垂直的判定定理与性质定理:
判定定理:如果一个平面经过另一个平面的垂线那么这两
个平面互相垂直(简记为“线面垂直 ? 面面垂直” )
?
l ⊥ α
符号语言: ?α ⊥ β
l ? β
性质定理:如果两个平面互相垂直,那么在一个平面内垂
直于它们交线的直线必垂直于另一个平面 (简记为“面面
垂直 ? 线面垂直” )
α ⊥ β
α ∩
β = l
符号语言: ?a⊥ α
a?
β
a⊥ l
总结:? 垂直问题基础理论
?
直角三角形——斜边上的中线
等腰梯形
垂直问题辅助线常规作法
过上顶点作线垂直于底
过底作两腰的反向延长线交于一点
第 25 页 共 99 页
1.4.3 系统法 1:面 ⊥ 面
系统法 1:面 ⊥ 面:
?
已知面垂直面
找交线
系统法 1:一面
谁垂直交线(不垂直,作垂直)
谁垂直另一个面
例 1(2018 天津 )
如图,在四面体 ABCD 中, ?ABC 是等边三角形,平面
ABC ⊥ 平面 ABD ,点 M 为棱 AB 的中点, AB = 2 , AD=
√ ?
2 3 , ∠ BAD = 90 .
( I ) 证明: AD⊥ BC .
分析
考查知识
答案
解答
由平面 ABC ⊥ 平面 ABD ;又
平面 ABC ∩ 平面 ABD = AB
且
AD⊥ AB
可得 AD⊥ 平面 ABC ,故
AD⊥ BC
变式练 1.1(2020 浙江 19 )
如图,三棱台 DEF ? ABC 中,面 ADF C ⊥ 面 ABC , ∠ ?
ACB = ∠ ACD = 45 , DC = 2 BC .
( I ) 证明: EF ⊥ DB ;
变式练 1.1 分析 考查知识
第 26 页 共 99 页
变式练 1.1
解答 ( I ) 如图,过点 D 作 DO ⊥ AC .交直线 AC 于点 O ,连结
OB . √
?
由 ∠ ACD = 45 , DO ⊥ AC 得 CD = 2 CO ,
由平面 ACF D ⊥ 平面 ABC 得 DO ⊥ 平面 ABC ,所以
DO ⊥ BC . √
由 ∠ ? 1 2
ACB = 45 , BC = CD = CO ,得 BO ⊥ BC .
2 2
所以 BC ⊥ 平面 BDO ,故 BC ⊥ DB .
变式练 1.2(2018 全国 III 理 19 )
? ?
如图,边长为 2 的正方形 ABCD 所在的平面与半圆弧 CD 所在平面垂直, M 是 CD 上异
于 C , D 的点.
( I ) 证明:平面 AMD ⊥ 平面 BMC ;
变式练 1.2 分析 考查知识
变式练 1.2
解答 ( I ) 由题设知,平面 CMD ⊥ 平面 ABCD ,交线为 CD .
因为 BC ⊥ CD , BC ? 平面 ABCD ,
所以
BC ⊥ 平面 CMD ,故 BC ⊥ DM .
?
因为 M 为 CD 上异于 C , D 的点,且 DC 为直径,
所以
DM ⊥ CM
又 BC ∩ CM = C ,所以 DM ⊥ 平面 BMC .
而 DM ? 平面 AMD ,
故平面 AMD ⊥ 平面 BMC .
第 27 页 共 99 页
1.4.4 系统法 2:二线
总结:?
两个三角形的三线合一
等腰三角形
系统法 2:二线
等边三角形
三线合一——中线,角平分线,高
例 1(2017 全国 III )
如图,四面体 ABCD 中, ?ABC 是正三角形, AD= CD .
( I ) 证明: AC ⊥ BD ;
分析
考查知识
答案
解答
证明:取 AC 的中点 O 连结 DO , BO ;
因为
AD= CD
所以
AC ⊥ DO
又由于 ?ABC 是正三角形,所以
AC ⊥ BO
从而 AC ⊥ 平面 DOB ,故 AC ⊥ BD .
第 28 页 共 99 页
变式练 1.1(2007 福建文 17 )
如图,正三棱柱 ABC ? A1 B 1 C 1 的所有棱长都为 2 , D 为
A A1
CC 1 的中点.
( I ) 求证: AB 1 ⊥ 平面 A1 BD ;
C C 1
D
B B 1
变式练 1.1 分析 考查知识
变式练 1.1
解答 ( I ) 证明:取 BC 的中点 O ,连接 AO .因为 △ ABC 为正
A A1
三角形,所以 AO ⊥ BC ;
因为正三棱柱 ABC ? A1 B 1 C 1 中,平面 ABC ⊥ 平面
BCC 1 B 1 ;
C C 1
AO ⊥ 平面 BCC 1 B 1 .连接 B 1 O ,在正方形 BB 1 C 1 C 中, D
O
O , D 分别为 BC , CC 1 的中点,所以所以 B 1 O ⊥ BD B B 1
, AO ⊥ BD .
所以 BD ⊥ 平面 AOB 1 ,则 BD ⊥ AB 1 ;
ABA 1 B 1 中, AB 1 ⊥ A1 B ,所以 AB 1 ⊥ 平面 A1 BD .
第 29 页 共 99 页
1.4.5 系统法 3:三勾股
系统法 3:三勾股:
?
勾股定理之逆定理证明垂直
常包含基本定理
系统法 3:三勾股
余弦定理
正弦定理
例 1(2010 江苏 )
如图,在三棱锥 P ? ABC 中, D, E , F 分别为棱 P C , AC ,
P
AB 的中点,已知 P A ⊥ AC , P A =6, BC =8, DF =5.
( I ) 求证:平面 BDE ⊥ 平面 ABC .
D
E C 1
A F B
分析
考查知识
答案
解答
因为 D , E 为 P C AC 中点,所以
1
DE = P A = 3
2
又因为 E , F 为 AC , AB 中点,所以
1
EF = BC = 4
2
且 DF =5,所以
2 2 2
DE + EF = DF
因为 ∠ ?
DEF = 90 ,所以
DE ⊥ EF
又因为 DE //P A P A ⊥ AC ,所以
DE ⊥ AC
又 AC ∩ EF = E ,所以 DE ⊥ 平面 ABC ,又 DE ? 平面 BDE ,所以
平面 BDE ⊥ 平面 ABC
第 30 页 共 99 页
变式练 1.1(2020 全国 I 理 18(2/5) )
如图, D 为圆锥的顶点, O 是圆锥底面的圆心, √ AE 为底面直径, AE = AD . △ ABC 是底
6
面的内接正三角形, P 为 DO 上一点, P O = DO
6
( I ) 证明 : P A ⊥ 平面 P BC
D
P
C
O
E B
A
变式练 1.1 分析 考查知识
变式练 1.1
解答 ( I ) 设 DO = a,由题设可得 √ √ √
6 3 2
P O = a, AO = a, AB = a, P A = P B = P C = a
6 3 2
2 2 2
因此 P A + P B = AB ,
从而
P A ⊥ P B
2 2 2
又 P A + P C = AC ;
故 P A ⊥ P C ,所以 P A ⊥ 平面 P BC .
变式练 1.2(2018 全国 II 文 19 ) √
如图,在三棱锥 P ? ABC 中, AB = BC = 2 2 , P A = P B = P C = AC = 4 , O 为 AC 的中
点.
( I ) 证明: P O ⊥ 平面 ABC ;
变式练 1.2 分析 考查知识
变式练 1.2
第 31 页 共 99 页
解答 ( I ) 连接 BO ,因为 P A = P C = 4 , O 为 AC 中点,
√
所以 P O ⊥ AC , P O = 2 3 ,
√
2 2
又因为 AB = BC = 2 2 , AC = 4 ,满足 AB + BC =
2
AC ,
所以 △ ABC 为等腰直角三角形,
所以 BO = 2 ,
在 △ 2 2 2
P OB 中, P B = 4 ,则 P O + BO = P B ,
则 P O ⊥ OB ,又因为 AC ∩ OB = O ,
所以 P O ⊥ 面 ABC . √
因为 AP = CP = AC = 4 , O 为 AC 的中点,所以 OP ⊥ AC ,且 OP = 2 3 .
连结 OB , √
2
因为 AB = BC = AC ,所以 △ ABC 为等腰直角三角形,且 OB ⊥ AC ,
2
1
OB = AC = 2 .
2
2 2 2
由 OP + OB = P B 知, OP ⊥ OB .
由 OP ⊥ OB , OP ⊥ AC 知 P O ⊥ 平面 ABC .
第 32 页 共 99 页
1.4.6 系统法 4:四图一柱
总结:?
四图
正方形——棱垂直棱、对角线垂直
菱形——对角线垂直
系统法 4:四图一柱 矩形——棱垂直棱
?
圆——直径所对圆周角 =90
一柱
直棱柱——侧棱垂直底面
例 1(四图一柱之正方形 )
已知四棱锥 S ? ABCD 的底面 ABCD 是正方形, SA ⊥ 底
面 ABCD , E 是 SC 上的任意一点 .
( I ) 求证:平面 EBD // 平面 SAC .
分析
考查知识
答案
解答
证明: SA ⊥ 平面 ABCD , BD ? 平面 ABCD ,所以
SA ⊥ BD
因为 ABCD 是正方形,所以
AC ⊥ BD
所以 BD ⊥ 平面 SAC ,又因为 BD ? 平面 EBD ;
所以
平面 EBD ⊥ 平面 SAC
第 33 页 共 99 页
变式练 1.1(2020 海南 20 )
如图,四棱锥 P ? ABCD 的底面为正方形, P D ⊥ 底面 ABCD .设平面 P AD 与平面 P BC
的交线为 l .
( I ) 证明: l ⊥ 平面 P DC ;
变式练 1.1 分析 考查知识
变式练 1.1
解答 ( I ) 在正方形 ABCD 中, AD// BC ,
因为
AD?? 平面 P BC , BC ? 平面 P BC
所以 AD// 平面 P BC ,
又因为 AD? 平面 P AD ,平面 P AD ∩ 平面 P BC = l ,
所以 AD// l ,
因为在四棱锥 P ? ABCD 中,底面 ABCD 是正方形,所以 AD⊥ DC ,
所以
l ⊥ DC ,且 P D ⊥ 平面 ABCD
所以 AD⊥ P D ,所以 l ⊥ P D ,
因 CD ∩ P D = D,所以 l ⊥ 平面 P DC .
变式练 1.2(2018 全国 I 理 18 )
如图,四边形 ABCD 为正方形, E, F 分别为 AD, BC 的中点,以 DF 为折痕把 △ DF C
折起,使点 C 到达点 P 的位置,且 P F ⊥ BF .
( I ) 证明:平面 P EF ⊥ 平面 ABF D ;
变式练 1.2 分析 考查知识
变式练 1.2
第 34 页 共 99 页
解答 ( I ) 证明:因为 E , F 分别为 AD, BC 的中点,四边形 ABCD 为正方形
所以 EF // AB , BC ⊥ AB ;
所以
BC ⊥ EF
因为 P F ⊥ BF ,
所以 P F ⊥ BC ,
而: EF ∩ P F = F
所以
BC ⊥ 平面 P EF
而: BC ? 平面 ABF D ,
∴ 平面 P EF ⊥ 平面 ABF D .
例 2(四图一柱之菱形 )
如图四边形 ABCD 为菱形, G 为 AC 与 BD 交点, BE ⊥
E
平面 ABCD .
( I ) 证明:平面 AEC ⊥ 平面 BED .
D C
A G
B
分析
考查知识
答案
解答
因为四边形 ABCD 为菱形,所以
AC ⊥ BD
因为 BE ⊥ 平面 ABCD ,所以
AC ⊥ BE
故 AC ⊥ 平面 BED .又 AC ? 平面 AEC ,所以
平面 AE ⊥ 平面 BED
第 35 页 共 99 页
四图一柱之圆
例 3(2013 辽宁 )
如图, AB 是圆 O 的直径, P A 垂直圆 O 所在的平面, C 是
圆 O 上的点.
( I ) 求证: BC ⊥ P AC .
分析
考查知识
答案
解答 证明:由 AB 是圆 O 的直径,得
AC ⊥ BC
由 P A ⊥ 平面 ABC , BC ? 平面 ABC ,得
P A ⊥ BC
又 P A ∩ AC = A, P A ? 平面 P AC , AC ? 平面 P AC ,所以
BC ⊥ 平面 P AC
变式练 3.1(2020 全国 II 理 20(4/5) )
如图 , 已知三棱柱 ABC ? A1 B 1 C 1 的底面是正三角形 , 侧面 BB 1 C 1 C 是矩形 , M , N 分别为
BC , B 1 C 1 的中点 , P 为 AM 上一点 . 过 B 1 C 1 和 P 的平面交 AB 于 E , 交 AC 于 F .
( I ) 证明 : AA1 // MN , 且平面 A1 AMN ⊥ 平面 EB 1 C 1 F ;
C 1
A1 O N
B 1
F C
A E P M
B
变式练 3.1 分析 考查知识
第 36 页 共 99 页
变式练 3.1
解答 ( I ) 因为 M, N 分别为 BC , B 1 C 1 的中点,所以
MN // CC 1
又由已知得 AA1 // CC 1 , 故
AA1 // MN
因为 △ A1 B 1 C 1 是正三角形,
所以 B 1 C 1 ⊥ A1 N . 又 B 1 C 1 // MN ,
故
B 1 C 1 ⊥ 平面 A1 AMN . 所以平面 A1 AMN ⊥ 平面 EB 1 C 1 F
第 37 页 共 99 页
1.4.7 系统法 5:五射影
总结:? ?
射影定理
系统法 5:五射影
点到射影面的射影线垂直射影面
例 1(五射影 )
如 图, 在 斜 三 棱 柱 ABC ? A1 B 1 C 1 中, AB = BC = 2 ,
∠ ?
ABC =120 ,又顶点 A1 在底面 ABC 上的射影落在 AC
上, M 为 AC 的中点
( I ) 求证: AA1 ⊥ BD .
分析
考查知识
答案
解答
在斜三棱柱 ABC ? A1 B 1 C 1 中,因为 A1 在底面 ABC 上的射影落在 AC 上,则平面
A1 ACC 1 经过底面 ABC 的垂线,故
侧面 A1 C ⊥ 平面 ABC
又因为侧面 A1 C ∩ 面 ABC =AC ,又 BD 为等腰 △ ABC 底边 AC 上中线,则
BD ⊥ AC
从而
BD ⊥ 平面 A1 C
又因为 AA1 ? 平面 A1 C ,所以
AA1 ⊥ BD
第 38 页 共 99 页
1.4.8 系统法 6:转化
总结:?
平行的传递性
垂直于同一平面的两条直线互相平行
系统法 6:六转化
两条直线互相平行,若其中一条垂直一个平面
则另一条直线也垂直于该平面
例 1(六转化 2015 新课标 )
如图,四边形 ABCD 为菱形, G 为 AC 与 BD 的交点, E
z
平面 ABCD .
E
( I ) 求证:平面 AEC ⊥ 平面 BED . F
H
B A y
OO G
O
C D
x
分析
考查知识
答案
解答
例题解答
第 39 页 共 99 页
1.4.9 平行垂直综合
例 1(2020 江苏 15 )
在三棱柱 ABC ? A1 B 1 C 1 中, AB ⊥ AC , B 1 C ⊥ 平面 ABC , E , F 分别是 AC , B 1 C 的中点.
( I ) 求证: EF // 平面 AB 1 C 1 ;
( II ) 求证:平面 AB 1 C ⊥ 平面 ABB 1 .
分析
考查知识
答案
解答
( I ) 因为 E , F 分别是 AC , B 1 C 的中点,所以 EF 是三角形 AB 1 C 的中位线,
所以
EF //AB 1
因为 EF ?? 平面 AB 1 C 1 , AB 1 ? 平面 AB 1 C 1 ,
所以
EF // 平面 AB 1 C 1
( II ) 因为 B 1 C ⊥ 平面 ABC , AB ? 面 ABC ,
所以
B 1 C ⊥ AB
又因为 AB ⊥ AC , AC ∩ B 1 C = C , AC ? 面 AB 1 C , B 1 C ? 面 AB 1 C ,
所以
AB ⊥ 面 AB 1 C
因为 AB ? 面 ABB 1 ,
所以
平面 AB 1 C ⊥ 平面 ABB 1
变式练 1.1(2019 北京文 18 )
如图,在四棱锥 P ? ABCD 中, P A ⊥ 平面 ABCD ,底面 ABCD 为菱形. E 为 CD 的中
点.
( I ) 求证: BD ⊥ 平面 P AC ;
?
( II ) 若 ∠ ABC = 60 ,求证:平面 P AB ⊥ 平面 P AE ;
(III) 棱 P B 上是否存在点 F ,使得 CF // 平面 P AE ?说明理由.
第 40 页 共 99 页
变式练 1.1 分析 考查知识
变式练 1.1
解答 ( I ) P A ⊥ 平面 ABCD ,且 BD ? 平面 ABCD ,
所以
P A ⊥ BD
在菱形 ABCD 中, AC ⊥ BD ,
即
P A ⊥ BD , P A ? 平面 P AC
AC ⊥ BD , AC ? 平面 P AC , P A ∩ AC = A,
所以
BD ⊥ 平面 P AC
( II ) P A ⊥ 平面 ABCD ,且 AE ? 平面 ABCD ,
所以
P A ⊥ AE
?
在菱形 ABCD 中, ∠ ABC = 60 ,
即 ∠ ?
ADC = 60
所以 △ ADC 为等边三角形,且 E 为 CD 中点.
所以
AE ⊥ CD
又 AB //CD , AE ⊥ AB ,
即
AE ⊥ P A , P A ? 平面 P AB
AE ⊥ AB , AB ? 平面 P AB , P A ⊥ AB = A,所以
AE ⊥ 平面 P AB ,且 AE ? 平面 P AE
所以平面 P AB ⊥ 平面 P AE .
第 41 页 共 99 页
(III) 棱 AB 上存在 F 点,且 F 为 P B 的中点,取 P A 中点
为 M ,
连接 MF 、 ME 、 F C ,因为 MF 分别 P A 、 P B 中点.
所以 1
MF //AB , MF = AB
2
因为底面 ABCD 为菱形,
所以 1
CE //AB , CE = AB
2
所以
MF //CE
所以四边形 MF CE 为平行四边形,
所以
F C //EM
因为 EM ? 平面 P AE , F C ?? 平面 P AE ,
所以
F C // 平面 P AE
变式练 1.2(2019 江苏 16 )
如图,在直三棱柱 ABC ? A1 B 1 C 1 中, D, E 分别为 BC , AC 的中点, AB = BC .求证:
( I ) A1 B 1 // 平面 DEC 1 ;
( II ) BE ⊥ C 1 E .
变式练 1.2 分析 考查知识
变式练 1.2
解答 ( I ) 因为 D, E 分别为 BC , AC 的中点,所以
ED // AB
在直三棱柱 ABC ? A1 B 1 C 1 中, AB // A1 B 1 ,
所以
A1 B 1 // ED
又因为 ED ? 平面 DEC 1 , A1 B 1 ?? 平面 DEC 1 ,
所以 A1 B 1 // 平面 DEC 1 .
因为 D, E 分别为 BC , AC 的中点,
第 42 页 共 99 页
所以
ED // AB
在直三棱柱 ABC ? A1 B 1 C 1 中, AB // A1 B 1 ,
所以
A1 B 1 // ED
又因为
ED ? 平面 DEC 1 , A1 B 1 ?? 平面 DEC 1
所以
A1 B 1 // 平面 DEC 1
( II ) 因为 AB = BC , E 为 AC 的中点,所以 BE ⊥ AC .
因为三棱柱 ABC ? A1 B 1 C 1 是直棱柱,所以 C 1 C ⊥ 平面 ABC .
又因为 BE ? 平面 ABC ,所以 C 1 C ⊥ BE .
因为
C 1 C ? 平面 A1 ACC 1 , AC ? 平面 A1 ACC 1 , C 1 C ∩ AC = C
所以 BE ⊥ 平面 A1 ACC 1 ,
因为 C 1 E ? 平面 A1 ACC 1 ,所以 BE ⊥ C 1 E .
变式练 1.3(2018 全国 III )
如图,矩形 ? ?
ABCD 所在的平面与半圆弧 CD 所在平面垂直, M 是 CD 上异于 C , D 的点.
( I ) 证明:平面 AMD ⊥ 平面 BMC ;
( II ) 在线段 AM 上是否存在点 P ,使得 MC // 平面 P BD ?说明理由.
变式练 1.3 分析 考查知识
变式练 1.3
解答 ( I ) 由题设知,平面 CMD ⊥ 平面 ABCD ,交线为 CD .
因为 BC ⊥ CD , BC ? 平面 ABCD ,
所以
BC ⊥ 平面 CMD ,故 BC ⊥ DM .
因为 ?
M 为 CD 上异于 C , D 的点,且 DC 为直径
所以 DM ⊥ CM .
又 BC ∩ CM = C ,所以
DM ⊥ 平面 BMC .
而 DM ? 平面 AMD ,故平面 AMD ⊥ 平面 BMC .
第 43 页 共 99 页
( II ) 当 P 为 AM 的中点时, MC // 平面 P BD .
证明如下:
连结 AC 交 BD 于 O .
因为 ABCD 为矩形,所以 O 为 AC 中点.
连结 OP ,因为 P 为 AM 中点,所以 MC // OP .
MC ?? 平面 P BD , OP ? 平面 P BD ,所以 MC // 平面
P BD .
变式练 1.4(2018 江苏 15 )
在平行六面体 ABCD ? A1 B 1 C 1 D1 中, AA1 = AB , AB 1 ⊥ B 1 C 1 .
( I ) 求证: AB // 平面 A1 B 1 C ;
( II ) 平面 ABB 1 A1 ⊥ 平面 A1 BC .
变式练 1.4 分析 考查知识
变式练 1.4
解答 ( I ) 因为平行六面体 ABCD ? A1 B 1 C 1 D1 .
所以面 ABC // 面 A1 B 1 C 1 D1 .
因为 A? B 面 ABCD .
所以 AB // 面 A1 B 1 C 1 D1 .
又面 ABA 1 B 1 ∩ 面 A1 B 1 C 1 D1 = A1 B 1 .
且 AB ? 面 ABA 1 B 1 .
所以 AB // A1 B 1 .
又 A1 B 1 ? 面 A1 B 1 C , AB ?? 面 A1 B 1 C .
所以 AB // 面 A1 B 1 C .
( II ) 由( 1 )可知: BC // B 1 C 1 .
因为 AB 1 ⊥ B 1 C 1 .
所以 AB 1 ⊥ BC .
因为平行六面体 ABCD ? A1 B 1 C 1 D1 .
所以 AB = A1 B 1 .
又由( 1)得 AB // A1 B 1 .
所以四边形 ABB 1 A1 为平行四边形.
第 44 页 共 99 页
因为 AA1 = AB 1 .
所以平行四边形 ABB 1 A1 为菱形.
所以 AB 1 ⊥ A1 B .
又 A1 B ∩ BC = C .
所以 AB 1 ⊥ 面 A1 BC .
因为 AB 1 ? 面 ABB 1 A1 .
所以面 ABB 1 A1 ⊥ 面 A1 BC .
变式练 1.5(2018 北京文 18 )
如图,在四棱锥 P ? ABCD 中,底面 ABCD 为矩形,平面 P AD ⊥ 平面 ABCD , P A ⊥ P D ,
P A = P D , E , F 分别为 AD, P B 的中点.
( I ) 求证: P E ⊥ BC ;
( II ) 求证:平面 P AB ⊥ 平面 P CD ;
(III) 求证: EF // 平面 P CD .
变式练 1.5 分析 考查知识
变式练 1.5
解答 ( I ) 在 △ P AD 中, P A = P D ,点 E 为 AD 中点,
所以 P E ⊥ AD ,
因为平面 P AD ⊥ 平面 ABCD ,
平面 P AD ∩ 平面 ABCD = AD , P E ? 平面 P AD ,
所以 P E ⊥ 平面 ABCD
因为 BC ? 平面 ABCD ,
所以 P E ⊥ BC .
( II ) 由( 1 )知 P E ⊥ 平面 ABCD ,
因为 CD ? 平面 ABCD ,
所以 P E ⊥ CD ,
又 CD ⊥ AD, P E , AD? 平面 P AD , P E ∩ AD= E ,
所以 CD ⊥ 平面 P AD ,
因为 P A ? 平面 P AD ,所以 CD ⊥ P A ,
因为 P A ⊥ P D , CD , P D ? 平面 P CD , CD ∩ P D = D,
所以 P A ⊥ 平面 P CD .
第 45 页 共 99 页
因为 P A ? 平面 P AB ,
所以平面 P AB ⊥ 平面 P CD .
(III) 取 P C 中点 Q ,连接 F Q , DQ ,
在 △ P BC 中, F , Q 分别为 P B , P C 中点,
所以 1
F Q // BC ,且 F Q = BC ,
2
因为 1
ED // BC ,且 ED = BC ,
2
所以 F Q // ED ,且 ED = F Q ,
所以四边形 EF QD 为平行四边形,
所以 EF // DQ , EF ?? 平面 P CD , DQ ? 平面 P CD ,
所以 EF // 平面 P CD .
变式练 1.6(2017 山东文 18 )
由四棱柱 ABCD ? A1 B 1 C 1 D1 截去三棱锥 C 1 ? B 1 CD 1 后得到的几何体如图所示,四边形
ABCD 为正方形, O 为 AC 与 BD 的交点, E 为 AD 的中点, A1 E ⊥ 平面 ABCD .
( I ) 证明: A1 O // 平面 B 1 CD 1 ;
( II ) 设 M 是 OD 的中点,证明:平面 A1 EM ⊥ 平面 B 1 CD 1 .
变式练 1.6 分析 考查知识
变式练 1.6
解答 ( I ) 证:取 B 1 D1 中点 F ,连接 A1 F , CF ,
因为 ABCD ? A1 B 1 C 1 D1 为四棱柱,
所以 A1 F // OC, A 1 F = OC ,
所以四边形 A1 F CO 为平行四边形,
所以 A1 O // CF ,
又 CF ? 平面 B 1 CD 1 , A1 O ?? 平面 B 1 CD 1 ,
所以 AO // 平面 B 1 CD 1 .
( II ) 因为 E 为 AD 的中点, M 为 OD 的中点,
所以 EM // AO ,因为四边形 ABCD 为正方形,
所以 AO ⊥ BD ,所以 EM ⊥ BD ,
又 A1 E ⊥ 平面 ABCD ,
所以 A1 E ⊥ BD ,所以 BD ⊥ 平面 A1 EM ,
又因为 B 1 D1 ? 平面 B 1 D1 C, BD // B 1 D1 ,
∴ B 1 D1 ⊥ 平面 A1 EM ,
第 46 页 共 99 页
又 B 1 D1 ? 平面 B 1 CD 1 ,
所以平面 A1 EM ⊥ 平面 B 1 CD 1 .
变式练 1.7(2017 北京文 18 )
如图,在三棱锥 P ? ABC 中, P A ⊥ AB , P A ⊥ BC , AB ⊥ BC , P A = AB = BC = 2 , D 为
线段 AC 的中点, E 为线段 P C 上一点.
( I ) 求证: P A ⊥ BD ;
( II ) 求证:平面 BDE ⊥ 平面 P AC ;
(III) 当 P A // 平面 BDE 时,求三棱锥 E ? BCD 的体积.
变式练 1.7 分析 考查知识
变式练 1.7
解答 ( I ) 因为 P A ⊥ AB , P A ⊥ BC , AB ∩ BC = B , AB , BC ? 平面 ABC .
所以
P A ⊥ 平面 ABC
因为
BD ? 平面 ABC
所以
P A ⊥ BD
( II ) 因为 AB = BC , D 为 AC 中点,
所以
BD ⊥ AC
又因为 BD ⊥ P A , P A ∩ AC = A,
所以 BD ⊥ 平面 P AC
因为
BD ? 平面 BDE
所以平面 BDE ⊥ 平面 P AC
(III) 因为 P A // 平面 BDE ,平面 P AC ∩ 平面 BDE = DE
所以 P A // DE ,
因为 P A ⊥ 平面 ABC ,
所以 DE ⊥ 平面 ABC
S △ 1 1
ABC = DC × BD = 1 , DE = P A = 1 ,
2 2
所以 1 1
V E ? BCD = S △ ABC × DE = .
3 3
因为 P A // 平面 BDE , P A ? 平面 P AC ,平面 P AC ∩ 平面 BDE = DE ,
所以 P A //DE ,
又 D 为 AC 中点, P A //DE ,
所以 DE 为 △ 1
CP A 中位线, E 为 P C 中点,且 DE = P A = 1 ,
2
由( 1 )得 P A ⊥ 平面 ABC , P A //DE ,
第 47 页 共 99 页
DE ⊥ 平面 ABC ,
所以 DE 为三棱锥 E ? BCD 的高,所以 1
V E ? BCD = | DE | · S △ BCD ,
3
1 1 1
S △ BCD = S △ ABC = · · 2 · 2 = 1 ,
2 2 2
1 1
V E ? BCD = · 1 · 1 = ,
3 3
所以三棱锥 E ? 1
BCD 的体积为 .
3
第 48 页 共 99 页
1.5 立体几何与空间向量
例 1(2018 上海 17 )
已知圆锥的顶点为 P ,底面圆心为 O ,半径为 2 .
( I ) 设圆锥的母线长为 4 ,求圆锥的体积.
?
( II ) 设 P O = 4 , OA , OB 是底面半径,且 ∠ AOB = 90 , M 为线段 AB 的中点,如图,求
异面直线 P M 与 OB 所成的角的大小(正切值).
分析
考查知识
答案
解答 √ √
( I ) h = 4 2 ? 2 2 = 2 3 , √
所以 1 2 8 3 π
V = πr h =
3 3
( II ) 取 OA 的中点 N ,
所以等价于求 ∠ P MN .
则 √ √
1
MN = OB = 1 , P N = P O 2 + ON 2 = 17
√ 2 √
所以 P N
tanθ = = 17 所以 θ = arc tan 17 .
MN
第 49 页 共 99 页
1.5.1 空间向量与线线角
例 1(2018 江苏 25 )
如图,在正三棱柱 ABC ? A1 B 1 C 1 中, AB = AA1 = 2 ,点 P , Q 分别为 A1 B 1 , BC 的中点.
( I ) 求异面直线 BP 与 AC 1 所成角的余弦值;
分析
考查知识
答案
解答
( I ) 设 AC , A1 C 1 的中点分别为 O , O 1 ,
则 OB ⊥ OC , OO 1 ⊥ OC , OO 1 ⊥ OB ,
# ? # ? # ?
故以 {OB, OC, OO 1 } 为基底,
建立空间直角坐标系 O ? xyz ,
因为 AB = AA1 = 2 , A(0 ,? 1 ,0) ,
√ √
B ( 3 ,0 ,0) , C (0 ,1 ,0) , A1 (0 ,? 1 ,2) , B 1 ( 3 ,0 ,2) ,
C 1 (0 ,1 ,2) .
点 P 为 √A1 B 1 的中点.
3
所以 1
P ( ,? ,2) ,
2 2 √
所以
# ? 3 1 # ?
BP = ? ,? ,2 , AC 1 = (0 ,2 ,2) .
2 2
# ? # ? √
# ? # ? | BP · AC | | ? 1 + 4 |
| 1 3 10
cos< BP , AC 1 > | = # ? # ? = √ √ = .
| BP | · | AC 1 | 5 × 2 2 20
√
3 10
所以异面直线 BP 与 AC 1 所成角的余弦值为: .
20
第 50 页 共 99 页
1.5.2 空间向量与点到面的距离
例 1(2019 上海 17 )
如图,在长方体 ABCD ? A1 B 1 C 1 D1 中, M 为 BB 1 上一点,已知 BM = 2 , CD = 3 , AD= 4 ,
AA1 = 5 .
( I ) 求直线 A1 C 与平面 ABCD 的夹角;
( II ) 求点 A 到平面 A1 MC 的距离.
分析
考查知识
答案
解答
( I ) 连接 AC , A1 C ,在长方体 ABCD ? A1 B 1 C 1 D1 中,
?
AA1 ⊥ AC ,所以 ∠ A1 AC = 90 ,因为 AD= 4 , CD = 3 ,
所以 AC = 5 ;
故
?
AC = AA1 , △ A1 AC 为等腰直角三角形, ∠ A1 CA = 45
?
故 A1 C 与平面 ABCD 所成的角 ∠ A1 CA = 45 .
( II ) 以 D 为中心, DA 为 x 轴, DC 为 y 轴, DD1 为 z
轴建立空间坐标系,
# ?
则 A1 (4 ,0 ,5) , C (0 ,3 ,3) , M (4 ,3 ,2) , A1 C = ( ? 4 ,3 ,? 5) ,
# ?
MC = ( ? #?
4 ,0 ,? 2) 设平面 A1 MC 的法向量 n =
( x, y, z
) ,
#? # ?
n · A1 C = 0 ? 4 x + 3 y ? 5 z = 0
则 即 ,
#? # ?
n · MC = 0 ? 4 x ? 2 z = 0
#? # ?
解得 n = ( ? 1 ,2 ,2) , A(4 ,0 ,0) , AC = ( ? 4 ,3 ,0) ,
# ?
# ? # ? #?
#? ·
故 A 到平面 A1 MC 的距离 = | AC | AC n 10
cos< AC, n > = = .
| #?n | 3
第 51 页 共 99 页
1.5.3 定义法与角度问题
例 1(2018 天津文 17 )
如图,在四面体 ABCD 中, △ ABC 是等边三角形,平面 ABC ⊥ 平面 ABD ,点 M 为棱
√ ?
AB 的中点, AB = 2 , AD= 2 3 , ∠ BAD = 90 .
( I ) 求证: AD⊥ BC ;
( II ) 求异面直线 BC 与 MD 所成角的余弦值;
(III) 求直线 CD 与平面 ABD 所成角的正弦值.
分析
考查知识
答案
解答 ( I ) 证明:由平面 ABC ⊥ 平面 ABD ,
平面 ABC ∩ 平面 ABD = AB ,
因为
AD⊥ AB
可得 AD⊥ 平面 ABC ,
故 AD⊥ BC .
( II ) 取棱 AC 的中点 N ,连接 MN , ND .
又因为 M 为棱 AB 的中点,故 MN // BC ,
所以 ∠ DMN (或其补角)为异面直线 BC 与 MD 所成
的角. √
在 Rt△ DAM 中, AM = 1 ,故 DM = AD2 + AM 2 =
√
13 .
因为 AD⊥ 平面 ABC ,
所以 AD⊥ AC ,
在 Rt△ DAN 中, AN = 1 ,
所以 √ √
DN = AD2 + AN 2 = 13
所以在等腰三角形 DMN 中, MN = 1 ,
可得 1 √
MN
2 13
cos∠ DMN = =
DM√ 26
13
所以异面直线 BC 与 MD 所成角的余弦值为 .
26
第 52 页 共 99 页
(III) 连接 CM ,因为 △ ABC 为等边三角形, M 为边 AB 的
中点, √
所以 CM ⊥ AB , CM = 3 ,
又因为平面 ABC ⊥ 平面 ABD ,而 CM ? 平面 ABC ,
所以 CM ⊥ 平面 ABD ,
即
∠ CDM 为直线 CD 与平面 ABD 所成的角.
√
在 Rt△ CAD 中, CD = AC 2 + AD2 = 4 √ .
3
在 CM
Rt△ CMD 中, sin∠ CDM = = .
CD 4 √
3
所以直线 CD 与平面 ABD 所成角的正弦值为 .
4
第 53 页 共 99 页
1.5.4 空间向量与线面角
例 1(2020 北京 16 )
如图,在正方体 ABCD ? A1 B 1 C 1 D1 中, E 为 BB 1 中点.
( I ) 求证: BC 1 // 平面 AD1 E .
( II ) 求直线 AA1 与平面 AD1 E 所成角的正弦值.
分析
考查知识
答案
解答
//
( I ) 在正方体 ABCD ? A1 B 1 C 1 D1 中, AB = C 1 D1 ,
所以四边形 ABC 1 D1 为平行四边形,则 AD1 // BC 1 ,
又因为 BC 1 ∈/ 平面 AD1 E , AD1 ? 平面 AD1 E ,
所以 BC 1 // 平面 AD1 E .
( II ) 在正方体 ABCD ? A1 B 1 C 1 D1 中,
AA1 ⊥ 平面 ABCD , AD⊥ AB ,
所以建立以 A为坐标原点, AD 所在直线为 x 轴, AB
所在直线为 y 轴, AA1 所在直线为 z 轴的空间直角
坐标.
设正方体 ABCD ? A1 B 1 C 1 D1 的边长为 2 ,
A(0 ,0 ,0) , A1 (0 ,0 ,2) , D1 (2 ,0 ,2) , E (0 ,2 ,1) ,
# ? # ? # ?
AA1 = (0 ,0 ,2) , AD1 = (2 ,0 ,2) , AE = (0 ,2 ,1) ,
#?
设平面
AD1 E 的法向量为 n
= ( x, y, z ) ,
#? # ?
n · AD1 = 0 2 x + 2 z = 0
所以 ,所以 ,令 y = 1 ,则 x = 2 , z = ? 2 ,
#? # ?
n · AE = 0 2 y + z = 0
#?
所以 n = (2 ,1 ,? 2) ,
设直线 AA1 与平面 AD1 E 所成的角为 θ ,
所以 # ?
# ?
#?
#?
AA1 · n ? 4
2
sinθ = | cos< AA1 , n > | =
# ?
= √
=
| #?
AA1 || n | 2 × 4 + 1 + 4 3
所以直线 2
AA1 与平面 AD1 E 所成角的正弦值为 .
3
第 54 页 共 99 页
变式练 1.1(2020 全国 II 理 20(4/5) )
如图 , 已知三棱柱 ABC ? A1 B 1 C 1 的底面是正三角形 , 侧面 BB 1 C 1 C 是矩形 , M , N 分别为
BC , B 1 C 1 的中点 , P 为 AM 上一点 . 过 B 1 C 1 和 P 的平面交 AB 于 E , 交 AC 于 F .
( I ) 证明 : AA1 // MN , 且平面 A1 AMN ⊥ 平面 EB 1 C 1 F ;
( II ) 设 O 为 △ A1 B 1 C 1 的中心 , 若 AO // 平面 EB 1 C 1 F , 且 AO = AB , 求直线 B 1 E 与平面
A1 AMN 所成角的正弦值 .
C 1
A1 O N
B 1
F C
A E P M
B
变式练 1.1 分析 考查知识
变式练 1.1
解答 ( I ) 因为 M, N 分别为 BC ,B 1 C 1 的中点 , 所以 MN // CC 1 . 又由已知得 AA1 // CC 1 , 故
AA1 // MN .
因为 △ A1 B 1 C 1 是正三角形 , 所以 B 1 C 1 ⊥ A1 N . 又 B 1 C 1 // MN , 故 B 1 C 1 ⊥ 平面
A1 AMN . 所以平面 A1 AMN ⊥ 平面 EB 1 C 1 F
# ?
( II ) 由已知得 AM ⊥ BC .以 M 为坐标原点, MA 的方向为
# ?
x 轴正方向, | MB | 为单位长,建立如图所示的空间直角
坐标系 M ? xyz , √
则 AB = 2 , AM = 3 ,连结 NP ,则四边形 AONP 为
平行四边形, √ √
2 3 2 3
故 1
P M = , E , ,0 ?? ,
3 3 3
由( 1 )知平面 A1 AMN ⊥ 平面 ABC .
作 NQ ⊥ AM ,垂足为 Q
,则 NQ ⊥ 平面 ABC .
√
2 √
2
2 3 2 3
设 Q ( a,0 ,0) ,则 NQ = 4 ? ? a , B 1 a,1 , 4 ? ? a ,
3 3
√ √
√
# ? 2
2 3 2 3 # ? 2 10
故 2
B 1 E = ? a,? ,? 4 ? ? a , B 1 E = ,
3 3 3 3
#?
又 n = (0 ,? 1 ,0) 是平面 A1 AMN 的法向量,
√
#? # ?
#? # ?
#? # ?
n · B E 10
故 π 1
sin ? n ?,B 1 E = cos n ?B 1 E =
# ?
2 | #?
= .
n | · B 1 E 10
√
10
所以直线 B 1 E 与平面 A1 AMN 所成角的正弦值为 .
10
第 55 页 共 99 页
变式练 1.2(2020 浙江 19 )
?
如图,三棱台 DEF ? ABC 中,面 ADF C ⊥ 面 ABC , ∠ ACB = ∠ ACD = 45 , DC = 2 BC .
( I ) 证明: EF ⊥ DB ;
( II ) 求 DF 与面 DBC 所成角的正弦值.
变式练 1.2 分析 考查知识
变式练 1.2
解答 ( I ) 如图,过点 D 作 DO ⊥ AC .交直线 AC 于点 O ,连结
OB . √
由 ∠ ?
ACD = 45 , DO ⊥ AC 得 CD = 2 CO ,
由平面 ACF D ⊥ 平面 ABC 得 DO ⊥ 平面 ABC ,所以
DO ⊥ BC . √
由 ∠ ? 1 2
ACB = 45 , BC = CD = CO ,得 BO ⊥ BC .
2 2
所以 BC ⊥ 平面 BDO ,故 BC ⊥ DB .
( II ) 由三棱台 ABC ? DEF 得 BC //EF ,所以 EF ⊥ DB .
过点 O 作 OH ⊥ BD ,交直线 BD 于点 H ,连结 CH .
由三棱台 ABC ? DEF 得 DF //CO ,所以直线 DF 与
平面 DBC 所成角等于直线 CO 与平面 DBC 所成角.
由 BC ⊥ 平面 BDO 得 OH ⊥ BC ,故 OH ⊥ 平面 BCD ,
所以 ∠ OCH 为直线 CO 与平面 DBC 所成角.
√
设 CD = 2 2 , √ √
由 DO = OC = 2 , BO = BC = 2 ,得 BD = 6 , OH =
√
2 3
3 √
3
所以 OH
sin∠ OCH = = ,
OC 3 √
3
因此,直线 DF 与平面 DBC 所成角的正弦值为 .
3
由三棱台 ABC ? DEF 得 DF //CO ,所以直线 DF 与平面 DBC 所成角等于直线 CO
与平面 DBC 所成角,记为 θ .
如图,以 O 为原点,分别以射线 OC , OD 为 y , z 轴的正半轴,建立空间直角坐标系
O ? xyz . √
设 CD = 2 2 .
由题意知各点坐标如下.
第 56 页 共 99 页
O (0 ,0 ,0) , B (1 ,1 ,0) , C (0 ,2 ,0) , D(0 ,0 ,2) .
# ? # ? # ?
因此 OC = (0 ,2 ,0) , BC = ( ? 1 ,1 ,0) , CD = (0 ,? 2 ,2) ,
设平面
BCD 的法向量
n = ( x, y, z ) .
# ?
n · BC = 0 ? x + y = 0
由 ,即 ,可取 n = (1 ,1 ,1) ,
# ?
n · CD = 0 ? 2 y + 2 z = 0
# ? √
# ? | OC · n |
所以 sinθ = | 3
cos< OC , n > | = # ? = .
| OC | · | n | 3 √
3
因此,直线 DF 与平面 DBC 所成角的正弦值为 .
3
变式练 1.3(2020 海南 20 )
如图,四棱锥 P ? ABCD 的底面为正方形, P D ⊥ 底面 ABCD .设平面 P AD 与平面 P BC
的交线为 l .
( I ) 证明: l ⊥ 平面 P DC ; √
( II ) 已知 P D = AD= 1 , Q 为 l 上的点, QB = 2 ,求 P B 与平面 QCD 所成角的正弦值.
变式练 1.3 分析 考查知识
变式练 1.3
解答 ( I ) 在正方形 ABCD 中, AD// BC ,
因为
AD?? 平面 P BC , BC ? 平面 P BC
所以 AD// 平面 P BC ,
又因为 AD? 平面 P AD ,平面 P AD ∩ 平面 P BC = l ,
所以 AD// l ,
因为在四棱锥 P ? ABCD 中,底面 ABCD 是正方形,所以 AD⊥ DC ,
所以
l ⊥ DC ,且 P D ⊥ 平面 ABCD
所以 AD⊥ P D ,所以 l ⊥ P D ,
因 CD ∩ P D = D,所以 l ⊥ 平面 P DC .
第 57 页 共 99 页
( II ) 如图建立空间直角坐标系 D? xyz ,因为 P D = AD= 1 ,
则 有 D(0 ,0 ,0) , C (0 ,1 ,0) , A(1 ,0 ,0) , P (0 ,0 ,1) ,
B (1 ,1 ,0) ,
# ? # ? # ?
设 Q ( m, 0 ,1) ,则有 DC = (0 ,1 ,0) , DQ = ( m, 0 ,1) , P B =
(1 ,1 ,? 1) , √
因为 QB ?
= 2 , √
2 2 2
所以有 ( m ? 1) + (0 ? 1) + (1 ? 0) = 2 ?m = 1 ,
#?
设平面
QCD 的法向量为
n = ( x, y, z ) ,
# ? #?
DC · n = 0 y = 0
则
# ? ,即 ,
#?
DQ · n = 0 x + z = 0
#?
令 x = 1 ,则 z = ? 1 ,所以平面 QCD 的一个法向量为 n = (1 ,0 ,? 1) ,
# ? √
#? # ? #? · 6
则 n P B 1 + 0 + 1 2
cos< n, P B > =
| #?
# ? ?
√ √
= √ = = ,
n | P B 1 2 + 0 2 + ( ? 2 × 3
1) · 1 2 + 1 2 + 1 2 2 3
根据直线的方向向量与平面法向量所成角的余弦值的绝对值即为直线与平面所成角的
正弦值, √
#? # ? 6
所以直线与平面所成角的正弦值等于 | cos< n, P B > | = ,
√ 3
6
所以直线 P B 与平面 QCD 所成角的正弦值为 .
3
变式练 1.4(2020 山东 20 )
如图,四棱锥 P ? ABCD 的底面为正方形, P D ⊥ 底面 ABCD .设平面 P AD 与平面 P BC
的交线为 l .
( I ) 证明: l ⊥ 平面 P DC ;
( II ) 已知 P D = AD= 1 , Q 为 l 上的点,求 P B 与平面 QCD 所成角的正弦值的最大值.
变式练 1.4 分析 考查知识
变式练 1.4
第 58 页 共 99 页
解答 ( I ) 如图在平面 P AD 内过点 A 作 AM // P D 且 AM = P D
连接 MP ,
所以
四边形 ADP M 是平行四边形
故有 MP // AD 且 MP = AD,又因为四边形 ABCD 为
正方形,
所以有 AD// BC 且 AD= BC ,所以有 P M // BC 且
P M = BC ,
故
直线 P M 就是平面 P AD 和平面 P BC 的交线 l
因为 P D ⊥ 底面 ABCD , P D ∩ DC = D 且 AD⊥ CD ,
所以 AD⊥ 平面 P CD ,所以 l ⊥ 平面 P CD .
( II ) 以 D 为坐标原点, DA 所在直线为 x 轴, DC 所在直线为 y 轴,
DP 所在直线为 z 轴,建立如图所示的空间直角坐标系,
则
D(0 ,0 ,0) , A(1 ,0 ,0) , B (1 ,1 ,0) , C (0 ,1 ,0) , P (0 ,0 ,1) , M (1 ,0 ,1)
# ? # ? # ?
设 Q ( t, 0 ,1)( t ∈ R) ,则 DQ = ( t, 0 ,1) , DC = (0 ,1 ,0) , P B = (1 ,1 ,? 1) ;
#?
令平面
QCD 的一个法向量为
n = ( x, y, z ) ,
#? # ?
n · DC = 0 y = 0
则 所以 ,
#? # ?
n · DQ = 0 tx + z = 0
#?
令 x = 1 ,则 y = 0 , z = ? t ,即 n = (1 ,0 ,? t ) ,
设 P B 与平面 QCD 所成角为
θ ,
# ? √ …
#?
#? # ?
n · P B | t + 1 | 3
则
2 t
sinθ = cos n · P B =
| #?
# ? √ ×
= = 1 +
2
n | · P B 3 t 2 + 3 3 t + 1
要使 sin…
θ 取到最大,显然 ?
t > 0 , √
因为 2 t 2
1 +
2 = 1 + ? 2 ,当且仅当 t = 1 时等号成立,
t + 1 1
t +
t
√
6
所以 sinθ ? ,
3 √
6
故平面 QCD 与 P B 所成角的正弦值最大为 .
3
变式练 1.5(2018 江苏 25 )
如图,在正三棱柱 ABC ? A1 B 1 C 1 中, AB = AA1 = 2 ,点 P , Q 分别为 A1 B 1 , BC 的中点.
( I ) 求异面直线 BP 与 AC 1 所成角的余弦值;
( II ) 求直线 CC 1 与平面 AQC 1 所成角的正弦值.
第 59 页 共 99 页
变式练 1.5 分析 考查知识
变式练 1.5
解答 ( I ) 设 AC , A1 C 1 的中点分别为 O , O 1 ,
则 OB ⊥ OC , OO 1 ⊥ OC , OO 1 ⊥ OB ,
# ? # ? # ?
故以 {OB, OC, OO 1 } 为基底,
建立空间直角坐标系 O ? xyz , √
因为 AB = AA1 = 2 , A(0 ,? 1 ,0) , B ( 3 ,0 ,0) , C (0 ,1 ,0) ,
√
A1 (0 ,? 1 ,2) , B 1 ( 3 ,0 ,2) , C 1 (0 ,1 ,2) .
点 P 为
A√
1 B 1 的中点.
3
所以 1
P ,? ,2 ,
2√ 2
# ? 3 # ?
所以 1
BP = ? ,? ,2 , AC 1 = (0 ,2 ,2) .
2 2
# ? # ? √
# ? # ? | BP · AC | | ? 1 + 4 |
| 1 3 10
cos< BP , AC 1 > | = # ? # ? = √ √ = .
| BP | · | AC 1 | 5 × 2 2 20
√
3 10
所以异面直线 BP 与 AC 1 所成角的余弦值为: .
√
20
3
( II ) 因为 Q 为 BC 的中点.所以 1
Q , ,0 ,
√
2 2
# ? 3 # ? # ?
所以 3
AQ = , ,0 , AC 1 = (0 ,2 ,2) , CC 1 = (0 ,0 ,2) ,
2 2
设平面 AQC 1 的一个法向量为 √ ?n = ( x, y, z ) ,
# ? 3 3
AQ · ?n = x + y = 0 √
由
2 2 ,可取 ?n = ( 3 ,? 1 ,1) ,
# ?
AC 1 · ?n = 2 y + 2 z = 0
设直线 CC 1 与平面 AQC 1 所成角的正弦值为 θ ,
# ? √
# ? | CC 1 · ?n | 2 5
sinθ = | cos< CC 1 , ?n > | = # ? = √ = ,
| CC 1 | · | ?n | 5 × 2 5
√
5
所以直线 CC 1 与平面 AQC 1 所成角的正弦值为 .
5
变式练 1.6(2018 全国 I 理 18 )
如图,四边形 ABCD 为正方形, E, F 分别为 AD, BC 的中点,以 DF 为折痕把 △ DF C
折起,使点 C 到达点 P 的位置,且 P F ⊥ BF .
第 60 页 共 99 页
( I ) 证明:平面 P EF ⊥ 平面 ABF D ;
( II ) 求 DP 与平面 ABF D 所成角的正弦值.
变式练 1.6 分析 考查知识
变式练 1.6
解答 ( I ) 证明:因为 E , F 分别为 AD, BC 的中点,四边形 ABCD 为正方形
所以 EF // AB , BC ⊥ AB ;
所以
BC ⊥ EF
因为 P F ⊥ BF ,
所以 P F ⊥ BC ,
而: EF ∩ P F = F
所以 BC ⊥ 平面 P EF
而: BC ? 平面 ABF D ,
∴ 平面 P EF ⊥ 平面 ABF D .
( II ) 作 P H ⊥ EF ,垂足为 H ,由( 1 )得, P H ⊥ 平面 ABF D ,
# ?
# ?
以
H 为坐标原点, HF 的方向为 y 轴正方向, BF 为
单位长,建立如图所示的空间直角坐标系 H ? xyz ,
由( 1 )可得, DE ⊥ P E ,又 DP = 2 , DE = 1 ,
√
所以 P E = 3 ,又 P F = 1 , EF = 2 ,故 P E ⊥ P F ,
√
可得 3 3
P H = , EH =
2 √
2
3
则 3
H (0 ,0 ,0) , P 0 ,0 , , D ? 1 ,? ,0 ,
√ √ 2
2
# ? 3 3 # ? 3
DP = 1 , , , HP = 0 ,0 , 为平面 ABF D 的
2 2 2
法向量,
设 DP 与平面 ABF D 所成角为 θ ,
3
√
# ? # ?
·
4 3
则
HP DP
sinθ =
# ? √ ,
# ?
= =
HP DP 3 4 √
3
所以 DP 与平面 ABF D 所成角的正弦值为 .
4
第 61 页 共 99 页
变式练 1.7(2018 全国 III 理 19 )
? ?
如图,边长为 2 的正方形 ABCD 所在的平面与半圆弧 CD 所在平面垂直, M 是 CD 上异
于 C , D 的点.
( I ) 证明:平面 AMD ⊥ 平面 BMC ;
( II ) 当三棱锥 M ? ABC 体积最大时,求面 MAB 与面 MCD 所成二面角的正弦值.
变式练 1.7 分析 考查知识
变式练 1.7
解答 ( I ) 由题设知,平面 CMD ⊥ 平面 ABCD ,交线为 CD .
因为 BC ⊥ CD , BC ? 平面 ABCD ,
所以
BC ⊥ 平面 CMD ,故 BC ⊥ DM .
?
因为 M 为 CD 上异于 C , D 的点,且 DC 为直径,
所以
DM ⊥ CM
又 BC ∩ CM = C ,所以 DM ⊥ 平面 BMC .
而 DM ? 平面 AMD ,故平面 AMD ⊥ 平面 BMC .
?
( II ) 以 D 为坐标原点, DA 的方向为 x 轴正方向,建立如图
所示的空间直角坐标系 D? xyz .
?
当三棱锥 M ? ABC 体积最大时, M 为 CD 的中点.
由 题 设 得 D(0 ,0 ,0) , A(2 ,0 ,0) , B (2 ,2 ,0) , C (0 ,2 ,0) ,
M (0 ,1 ,1) ,
# ? # ? # ?
AM = ( ? 2 ,1 ,1) , AB = (0 ,2 ,0) , DA= (2 ,0 ,0) .
#?
设
n = ( x, y, z ) 是平面 MAB
的法向量,
#? # ?
n · AM = 0 , ? 2 x + y + z = 0 , # ?
则 即 可取 n = (1 ,0 ,2) . DA 是平面 MCD
#? # ?
n · AB = 0 . 2 y = 0 .
的法向量, √
#? # ?
#? # ? · 5
因此 n DA
cos( n, DA) =
# ?
= ,
| #?
√ n | DA 5
#? # ? 2 5
故 sin( n, DA) = ,
5 √
2 5
所以面 MAB 与面 MCD 所成二面角的正弦值是 .
5
第 62 页 共 99 页
变式练 1.8(2018 浙江 19 )
?
如图,已知多面体 ABCA 1 B 1 C 1 , A1 A, B 1 B , C 1 C 均垂直于平面 ABC , ∠ ABC = 120 , A1 A= 4 ,
C 1 C = 1 , AB = BC = B 1 B = 2 .
( I ) 证明: AB 1 ⊥ 平面 A1 B 1 C 1 ;
( II ) 求直线 AC 1 与平面 ABB 1 所成的角的正弦值.求直线 AC 1 与平面 ABB 1 所成的角的
正弦值.
变式练 1.8 分析 考查知识
变式练 1.8
解答 ( I ) 过 B 1 作 B 1 E ⊥ AA1 于点 E ,
过 C 1 作 C 1 F ⊥ BB 1 于点 F ,
B 1 E = AB = 2 , AE = BB 1 = 2 , A1 E = 2 ,
√
所以 A?
1 B 1 = A 2 2
1 E + B 1 E = 2 2 ,
√
2
AB 2
1 = BB 1 + AB = 2 2 ,
AA1 = 4 ,
2 2 2
所以 A1 B 1 + AB 1 = AA1 ,
所以 AB 1 ⊥ A1 B 1 ,
又 C 1 F = BC = 2 ,B 1 F = 1 ,
√ √
所以 B 1 C 1 = C 2 2
?
1 F + B 1 F = 5 , AC = 2 3 ,
√
2
所以 AC 1 = AC 2 + CC 1 = 13 ,
2 2 2
所以 A1 B 1 + B 1 C 1 = AC 1 ,
所以 AB 1 ⊥ B 1 C 1 ,
因为 B 1 C 1 ? 平面 A2 B 1 C 1 ,
A1 B 1 ? 平面 A1 B 1 C 1 ,
所以 AB 1 ⊥ 平面 A1 B 1 C 1 .
由题意得 BB 1 ⊥ AB , CC 1 ⊥ BC , AA1 ⊥ AB ,
所以 △ ABB 1 为直角三角形,四边形 BCC 1 B 1 为直角梯形.
√
所以 AB 1 = 2 2 , √
在 △ ?
ABC 中, AB = 2 , BC = 2 , ∠ ABC = 120 ,由余弦定理得 AC = 2 3 ,
√
在 △ ACC 1 中,由勾股定理得 AC 1 = 13 ,
第 63 页 共 99 页
√ √
同理, A1 B 1 = 2 2 在直角梯形 BCC 1 B 1 中可得 B 1 C 1 = 5 ,
2 2 2 ?
则 A1 B 1 + AB 1 = AA1 ,所以 ∠ AB 1 A1 = 90 ,
所以 AB 1 ⊥ A1 B 1 .
同理, AB 1 ⊥ B 1 C 1 .
又 A1 B 1 ∩ B 1 C 1 = B 1 ,
所以 AB 1 ⊥ 平面 A1 B 1 C 1 .
( II ) 以 A 为原点, Ax 为 x 轴, AC 为 y 轴, AA1 为 z 轴建
立空间直角坐标系, √ √
则: A(0 ,0 ,0) , A1 (0 ,0 ,4) , B (1 , 3 ,0) , B 1 (1 , 3 ,2) ,
√
C 1 (0 ,2 3 ,1) ,
# ? √
# ? √
# ?
所以 AC 1 = (0 ,2 3 ,1) , AB 1 = (1 , 3 ,2) , AA1 = (0 ,0 ,4) ,
#?
设 n = ( x, y, z ) 的法向量,
√
x + 3 y + 2 z = 0 , 4 z = 0 ,
√
#?
所以 n = ( ? 3 ,
1 ,0) ,
# ? √ √
#?
# ? #?
AC · n 2 3 39
sin AC · n =
# ? √ ,
#? = =
√ AC · | n | 2 13 13
39
所以正弦值是 .
13
如图,作 CH ⊥ AB ,垂足为 H ,
结合 CH ⊥ BB 1 知 CH ⊥ 平面 A1 ABB 1 ,
又 CC 1 // 平面 AA1 B 1 B ,
所以 CH 为 C 1 到平面 A1 ABB 1 的距离.
?
在 △ BCH 中得 ∠ CBH = 60 , BC = 2 , √ √
√
3 39
所以 CH
CH = 3 所以直线 AC 1 与平面 ABB 1 所成的角的正弦值为 = √ = .
AC 1 13 13
第 64 页 共 99 页
1.5.5 空间向量与二面角
例 1(2020 全国 I 理 18(2/5) )
如图, D 为圆锥的顶点, O 是圆锥底面的圆心, √ AE 为底面直径, AE = AD . △ ABC 是底
6
面的内接正三角形, P 为 DO 上一点, P O = DO
6
( I ) 证明 : P A ⊥ 平面 P BC
( II ) 求二面角 B ? P C ? E 的余弦值 .
D
P
C
O
E B
A
分析
考查知识
答案
解答 √ √ √
6 3 2
( I ) 设 DO = a,由题设可得 P O = a, AO = a, AB = a, P A = P B = P C = a,
6 3 2
2 2 2 2 2 2
因此 P A + P B = AB ,从而 P A ⊥ P B ,又 P A + P C = AC ;
故 P A ⊥ P C ,所以 P A ⊥ 平面 P BC .
# ? # ?
( II ) 以 O 为坐标原点, OE 的方向为 y 轴正方向, | OE | 为单
位长,建立如图所示的空间直角坐标系 O ? xyz √ .
3
由 题 设 可 得 1
E (0 ,1 ,0) , A(0 ,? 1 ,0) , C ( ? , ,0) ,
√ 2 2
2
P (0 ,0 , ) ,
2 √ √
# ? 3 # ? 2 #?
所以 1
EC = ( ? ,? ,0) , EP = (0 ,? 1 , ) ,设 m =
2 2 2
( x, y, z ) 是平面 P CE 的法向量,
则 √
?
2
#? # ? ? y + z = 0 √
m · EP = 0 √
√ 2 #? ? 3
#? # ? , ,可取 m = ,1 , 2 ;
m · EC = 0
3 1 3
? x ? y = 0
2 √
2
# ? 2 #? # ?
由( 1 )知 AP = 0 ,1 , 是平面 P CB 的一个法向量,记 n = AP ,
2 √ √
#? #?
#? #? · 2 5 2 5
则 n m
cos? n, m ? = = ,故二面角 B ? P C ? E 的余弦值为 .
| #? #?
n | · | m | 5 5
第 65 页 共 99 页
例 2(2007 福建文 17 )
如图,正三棱柱 ABC ? A1 B 1 C 1 的所有棱长都为 2 , D 为
A A1
CC 1 的中点.
( I ) 求证: AB 1 ⊥ 平面 A1 BD ;
( II ) 求二面角 A? A1 D? B 的大小(余弦值).
C C 1
D
B B 1
分析
考查知识
答案
解答
( I ) 证明:取 BC 的中点 O ,连接 AO .因为 △ ABC 为
A A1
正三角形,所以 AO ⊥ BC ;
因为正三棱柱 ABC ? A1 B 1 C 1 中,平面 ABC ⊥ 平面
BCC 1 B 1 ;
C C 1
AO ⊥ 平面 BCC 1 B 1 .连接 B 1 O ,在正方形 BB 1 C 1 C D
O
中, O , D 分别为 BC , CC 1 的中点,所以所以 B B 1
B 1 O ⊥ BD , AO ⊥ BD .
所以 BD ⊥ 平面 AOB 1 ,则 BD ⊥ AB 1 ;
ABA 1 B 1 中, AB 1 ⊥ A1 B ,所以 AB 1 ⊥ 平面 A1 BD .
# ? # ? # ?
( II ) 取 B 1 C 1 的中点 O 1 ,以 O 为原点, OB , OO 1 , OA
z
的方向为 x , y , z 轴的正方向建立空间直角坐标系; √ √ A A1
则 B (1 ,0 ,0) , D( ? 1 ,1 ,0) , A1 (0 ,2 , 3) , A(0 ,0 , 3) ,
# ?
B 1 (1 ,2 ,0) 由( 1)知 AB 1 ⊥ 平面 A1 BD ,所以 AB 1 =
√
(1 ,2 ,? 3) 为平面 A1 BD 的一个法向量. C C 1
#? # ?
设 平 面 A1 AD 的 法 向 量 为 n = ( x, y, z ) . AD= D y
√
# ? OO
? 1 ,1 ,? 3 ,AA1 = (0 ,2 ,0) . B B 1
x
√
#? # ?
n · AD= 0 , ? x + y ? 3 z = 0 , y = 0 ,
所以 所以 则 ;
√
#? # ?
n · AA1 = 0 , 2 y = 0 , x = ? 3 z
#? √
令 z = 1 得 n = ? 3 ,0 ,1 为平面 A1 AD 的一个法向量.所以 √ √ √
# ?
#? # ?
#?n · AB 1 ? 3 ? 3 6
cos n ?AB 1 =
# ?
= √ = ?
| #?
n | AB 1 2 × 2 2 4 √
6
由于二面角 A? A1 D? B 为锐角,故二面角 A? A1 D? B 的余弦值为 .
4
第 66 页 共 99 页
例 3(2020 天津 17 )
如图,在三棱柱 ABC ? A1 B 1 C 1 中, CC 1 ⊥ 平面 ABC , AC ⊥ BC , AC = BC = 2 , CC 1 = 3 ,
点 D, E 分别在棱 AA1 和棱 CC 1 上,且 AD= 1 , CE = 2 , M 为棱 A1 B 1 的中点.
( I ) 求证: C 1 M ⊥ B 1 D;
( II ) 求二面角 B ? B 1 E ? D 的正弦值;
(III) 求直线 AB 与平面 DB 1 E 所成角的正弦值.
分析
考查知识
答案
解答
# ? # ? # ?
( I ) 依题意,以 C 为原点,分别以 CA , CB , CC 1 的方向
为 x 轴, y 轴, z 轴的正方向建立空间直角坐标系(如
图),可得 C (0 ,0 ,0) , A(2 ,0 ,0) , B (0 ,2 ,0) , C 1 (0 ,0 ,3) ,
A1 (2 ,0 ,3) , B 1 (0 ,2 ,3) , D(2 ,0 ,1) , E (0 ,0 ,2) , M (1 ,1 ,3) ,
# ? # ?
C 1 M = (1 ,1 ,0) , B 1 D= (2 ,? 2 ,? 2) ,
# ? # ?
从而 C 1 M · B 1 D= 2 ? 2 + 0 = 0 ,所以 C 1 M ⊥ B 1 D.
# ? # ? # ?
( II ) 依题意, CA = (2 ,0 ,0) 是平面 BB 1 E 的一个法向量,
EB 1 = (0 ,2 ,1) , ED =
# ?
·
#? n EB 1 = 0
(2 ,0 ,? 1) ,设 n = ( x, y, z ) 为平面 DB 1 E 的法向量,则
# ?
n · ED = 0
2 y + z = 0
#?
# ? #?
即 ,不妨设 x = 1 ,可得 n = (1 ,? 1 ,2) ,因此有 cos CA ?n =
2 x ? z = 0
# ? √ √
#?
CA · n 6 # ? #? 30
# ? = ,于是 sin CA ?n = ,所以二面角 B ? B 1 E ? D 的正弦值
| #?
CA√ | | n | 6 6
30
为 .
6
# ? #?
(III) 依题意, AB = ( ? 2 ,2 ,0) ,由( 2 )知 √ n = (1 ,? 1 ,2) √为平面 DB
# ? 1 E 的一个法向量,
# ? #?
· #? 3 3
于是 AB n
cos AB ?n =
# ? ? .故正弦值为 .
#? =
AB | n | 3 3
第 67 页 共 99 页
变式练 3.1(2020 全国 III 理 19 )
如图,在长方体 ABCD ? A1 B 1 C 1 D1 中,点 E , F 分别在棱 DD1 , BB 1 上,且 2 DE = ED 1 ,
BF = 2 F B 1 .
( I ) 证明:点 C 1 在平面 AEF 内;
( II ) 若 AB = 2 , AD= 1 , AA1 = 3 ,求二面角 A? EF ? A1 的正弦值.
变式练 3.1 分析 考查知识
变式练 3.1
解答 ( I ) 在 AA1 上取一三等分点 M ,使得 A1 M = 2 AM ,分别连
接 EM , B 1 M , EC 1 , F C 1 ,
在长方体 ABCD ? A1 B 1 C 1 D1 中,有 DD1 //AA1 //BB 1 ,
且 DD1 = AA1 = BB 1 ,
又 2 DE = ED 1 , A1 M = 2 AM , BF = 2 F B 1 ,
所以 DE = AM = F B 1 ,
即
四边形 B 1 AF M 与 EDAM 都是平行四边形
所以 AF //MB 1 且 AF = MB 1 , AD= ME 且 AD//ME ,
又在长方体中,有 AD//B 1 C 1 且 AD= B 1 C 1 ,
所以
B 1 C 1 //ME 且 B 1 C 1 = ME
则
四边形 B 1 C 1 EM 为平行四边形
所以 EC 1 //MB 1 且 EC 1 = MB 1 ,
又
AF //MB 1 且 AF = MB 1
所以
AF //EC 1 且 AF = EC 1
则
四边形 AF C 1 E 为平行四边形
故点 C 1 在平面 AEF 内.
第 68 页 共 99 页
( II ) 在长方体中,以 C 1 为原点, C 1 D1 所在直线为 x 轴, C 1 B 1
所在直线为 y 轴, C 1 C 所在直线为 z 轴,建立如图所示空
间直角坐标系.因为 AB = 2 , AD= 1 , AA1 = 3 , 2 DE =
ED 1 , BF = 2 F B 1 ,所以 A(2 ,1 ,3) , E (2 ,0 ,2) , F (0 ,1 ,1) ,
A1 (2 ,1 ,0) ,
# ? # ? # ?
则 EF = ( ? 2 ,1 ,? 1) , AE = (0 ,? 1 ,? 1) , A1 E = (0 ,? 1 ,2) ,
#?
设平面
AEF 的一个法向量为
n 1 = ( x 1 , y 1 , z 1 ) ,
#? # ?
n 1 · EF = 0 ? 2 x 1 + y 1 ? z 1 = 0
则 ,即 ,
#? # ?
n 1 · AE = 0 ? y 1 ? z 1 = 0
#?
令 x 1 = 1 ,则 y 1 = 1 , z 1 = ? 1 ,即 n 1 = (1 ,1 ,? 1) .
#?
设平面
A1 EF 的一个法向量为
n 2 = ( x 2 , y 2 , z 2 ) ,
#? # ?
n 2 · EF = 0 ? 2 x 2 + y 2 ? z 2 = 0
#?
则 ,即 ,令 x = 1 ,则 y = 4 , z = 2 ,即 n =
2 2 2 2
#? # ?
n 2 · A1 E = 0 ? y 2 + 2 z 2 = 0
(1 ,4 ,2) ,
所以 #? #? √
#? #? n 1 · n 2 1 + 4 ? 2 7
cos? n 1 · n 2 ? = | #? #? = √ √ =
n 1 | · | n 2 | 3 · 21 7
设二面角 A? EF ? A1 为 θ ,则 …
√
1 42
sinθ = 1 ? =
7 7 √
即 42
二面角 A? EF ? A1 的正弦值为 7
变式练 3.2(2020 江苏理 24 ) √
在三棱锥 A? BCD 中,已知 CB = CD = 5 , BD = 2 , O 为 BD 的中点, AO ⊥ 平面 BCD ,
AO = 2 , E 为 AC 的中点.
( I ) 求直线 AB 与 DE 所成角的余弦值;
1
( II ) 若点 F 在 BC 上,满足 BF = BC ,设二面角 F ? DE ? C 的大小为 θ ,求 sinθ 的
4
值.
变式练 3.2 分析 考查知识
第 69 页 共 99 页
变式练 3.2
解答 ( I ) 连结 OC ,
因为 CB = CD , O 为 BD 中点,
所以 CO ⊥ BD ,又 AO ⊥ 平面 BCD ,
所以 AO ⊥ OB , AO ⊥ OC .
# ? # ? # ?
以 OB, OC, OA 为基底,建立空间直角坐标系 O ?
xyz . √
因为 BD = 2 , CB = CD = 5 , AO = 2 ,
所以 B (1 ,0 ,0) , D( ? 1 ,0 ,0) , C (0 ,2 ,0) , A(0 ,0 ,2) .
则
# ? # ?
AB = (1 ,0 ,? 2) , DE = (1 ,1 ,1)
所以 # ? # ? √
# ? # ? | AB · DE | | 1 + 0 ? 2 |
| cos? 15
AB, DE ?| = # ? # ? = √ √ =
| AB | · | DE√ | 5 × 3 15
15
因此,直线 AB 与 DE 所成角的余弦值为 .
15
1 # ?
( II ) 因为点 F 在 BC 上, BF = BC , BC = ( ? 1 ,2 ,0) ,
4
所以
# ? 1 # ? 1 1
BF = BC = ? , ,0
# ? 4 4 2
又 DB = (2 ,0 ,0) ,故
# ? # ? # ? 7 1
DF = DB + BF = , ,0
4 2
#?
设 n 1 = ( x 1 , y 1 , z 1 ) 为平面 DEF 的一个法向量,
# ? #?
DE · n 1 = 0 x 1 + y 1 + z 1 = 0
#?
则
# ? ,即 取 x 1 = 2 ,得 y 1 = ? 7 , z 1 = 5 ,所以 n 1 =
#?
7 1
DF · n 1 = 0 x 1 + y 1 = 0
4 2
(2 ,? 7 ,5) .
#? # ?
设
n 2 = ( x 2 , y 2 , z 2 ) 为平面
DEC 的一个法向量,又 DC = (1 ,2 ,0) ,
# ? #?
DE · n 2 = 0 x 2 + y 2 + z 2 = 0
则
# ? ,即 ,取 x 2 = 2 ,得 y 2 = ? 1 ,得 z 2 = ? 1 ,所以
#?
DC · n 2 = 0 x 2 + 2 y 2 = 0
#?
n 2 = (2 ,? 1 ,? 1) .
故 | #? #? √
n · n | | 4 + 7 ? 5 |
| 1 2
cosθ | 13
= = √ √ =
| #? #?
√ n 1 | · | n 2 | 78 × 6 13
√
2 39
所以 sinθ = 1 ? cos2 θ = .
13
变式练 3.3(2019 全国 III 理 19 )
图 1 是由矩形 ADEB , Rt△ ABC 和菱形 BF GC 组成的一个平面图形,其中 AB = 1 , BE =
?
BF = 2 , ∠ F BC = 60 .将其沿 AB , BC 折起使得 BE 与 BF 重合,连结 DG ,如图 2 .
( I ) 证明:图 2 中的 A, C , G , D 四点共面,且平面 ABC ⊥ 平面 BCGE ;
第 70 页 共 99 页
( II ) 求图 2 中的二面角 B ? CG ? A 的大小.
变式练 3.3 分析 考查知识
变式练 3.3
解答 ( I ) 由已知得 AD// BE , CG // BE ,
所以
AD// CG ,故 AD, CG 确定一个平面
从而 A, C , G , D 四点共面.
由已知得
AB ⊥ BE , AB ⊥ BC
故
AB ⊥ 平面 BCGE
又因为 AB ? 平面 ABC ,
所以
平面 ABC ⊥ 平面 BCGE
( II ) 作 EH ⊥ BC ,垂足为 H .
因为 EH ? 平面 BCGE ,平面 BCGE ⊥ 平面 ABC ,
所以
EH ⊥ 平面 ABC
?
由已知,菱形 BCGE 的边长为 2 , ∠ EBC = 60 ,
可求得 √
BH = 1 , EH = 3
# ?
以 H 为坐标原点, HC 的方向为 x 轴的正方向,
建立如图所示的空间直角坐标系 H √ ? xyz ,
# ? √
# ?
则 A( ? 1 ,1 ,0) , C (1 ,0 ,0) , G (2 ,0 , 3) , CG = (1 ,0 , 3) , AC = (2 ,? 1 ,0) .
#?
设平面
ACGD 的法向量为
n = ( x, y, z ) ,
√
# ? #?
CG · n = 0 x + 3 z = 0 √
#?
则 ?
# ? ,即 .所以可取 n = (3 ,6 , 3) .
#?
AC · n = 0 2 x ? y = 0
#?
又平面 BCGE 的法向量可取为 m = (0 ,1 ,0) ; √
所以 #? #?
#? #? n · m 3
cos? n, m ? = =
| #? #?
n || m | 2
因此
二面角 B ? CG ? ?
A 的大小为 30
第 71 页 共 99 页
变式练 3.4(2019 全国 II 理 17 )
如图,长方体 ABCD ? A1 B 1 C 1 D1 的底面 ABCD 是正方形,点 E 在棱 AA1 上, BE ⊥ EC 1 .
( I ) 证明: BE ⊥ 平面 EB 1 C 1 ;
( II ) 若 AE = A1 E ,求二面角 B ? EC ? C 1 的正弦值.
变式练 3.4 分析 考查知识
变式练 3.4
解答 ( I ) 由已知得 B 1 C 1 ⊥ 平面 ABB 1 A1 , BE ? 平面 ABB 1 A1 ,
故
B 1 C 1 ⊥ BE
又
BE ⊥ EC 1
所以
BE ⊥ 平面 EB 1 C 1
?
( II ) 由 I 知 ∠ BEB 1 = 90 .
? ?
由题设知 Rt △ ABE = Rt △ A1 B 1 E ,所以 ∠ AEB = 45 ,
故
AE = AB , AA1 = 2 AB
# ? # ?
以 D 为坐标原点, DA 的方向为 x 轴正方向, | DA| 为
单位长,建立如图所示的空间直角坐标系 D? xyz ,
# ?
则 C (0 ,1 ,0) , B (1 ,1 ,0) , C 1 (0 ,1 ,2) , E (1 ,0 ,1) , CE =
# ?
(1 ,? 1 ,1) , CC 1 = (0 ,0 ,2) .
#?
设平面 EBC 的法向量为 n = ( x 1 , y 1 , z 1 ) ,
?
# ? ?
#?
CB · n = 0 , x 1 = 0 ,
#?
则 # ? #? 即 所以可取 n = (0 ,? 1 ,? 1) .
CE · n = 0 , x 1 ? y 1 + z 1 = 0 ,
#?
设平面 ECC 1 的法向量为 m = ( x
?
2 , y 2 , z 2 ) ,
# ? ?
#?
CC 1 · m = 0 , 2 z 2 = 0 ,
#?
则 # ? #? 即 所以可取 m = (1 ,1 ,0) .
CE · m = 0 , x 2 ? y 2 + z 2 = 0 .
#? #?
#? #? ·
于是 n m 1
cos< n, m > = | #? #? = ? .
n | · | m | 2 √
3
所以,二面角 B ? EC ? C 1 的正弦值为 .
2
第 72 页 共 99 页
变式练 3.5(2019 天津理 17 )
如图, AE ⊥ 平面 ABCD , CF // AE , AD// BC , AD⊥ AB , AB = AD= 1 , AE = BC = 2 .
( I ) 求证: BF // 平面 ADE ;
( II ) 求直线 CE 与平面 BDE 所成角的正弦值;
(III) 若二面角 E ? 1
BDF 的余弦值为 ,求线段 CF 的长.
3
变式练 3.5 分析 考查知识
变式练 3.5
# ? # ? # ?
解答 ( I ) 依题意,可以建立以 A 为原点,分别以 AB , AD, AE
的方向为 x 轴, y 轴, z 轴正方向的空间直角坐标系(如
图),
可得 A(0 ,0 ,0) , B (1 ,0 ,0) , C (1 ,2 ,0) , D(0 ,1 ,0) , E (0 ,0 ,2) .
设 CF = h ( h > 0) ,则 F (1 ,2 , h ) .
# ? # ?
依题意, AB = (1 ,0 ,0) 是平面 ADE 的法向量,又 BF =
# ? # ?
(0 ,2 , h ) ,可得 BF · AB = 0 ,
又因为直线 BF ?? 平面 ADE ,所以 BF // 平面 ADE .
# ? # ? # ?
( II ) 依题意, BD = ( ? 1 ,1 ,0) , BE = ( ? 1 ,0 ,2) , CE = ( ? 1 ?
2 ,2) ,
#? # ?
·
?
#? n BD = 0 x + y = 0
设 n = ( x, y, z ) 为平面 BDE 的法向量,则 ,即 ,
#? # ?
n · BE = 0 ? x + 2 z = 0
# ?
#?
# ? #?
#? | CE · n |
不妨令 4
z = 1 ,可得 n = (2 ,2 ,1) ,因此有 | cos CE, n | = # ? = .
| #?
CE | · | n | 9
故直线 4
CE 与平面 BDE 所成角的正弦值为 .
9
#?
(III) 设
m = ( x, y, z ) 为平面
BDF 的法向量,
#? # ?
m · BD = 0 ? x + y = 0
#?
则 ,即 ,不妨令 2
y = 1 ,可得 m = 1 ,1 ,? ,
#? # ?
h
m · BF = 0 2 y + hz = 0
2
#? #?
4 ?
m · n h
由题意,有 | #? #? 1
cos? m, n ?| = = ?
= ,
| #? #?
m || n | 4 3
3 2 +
2
h
解得 8 8
h = ,经检验,符合题意.所以,线段 CF 的长为 .
7 7
第 73 页 共 99 页
变式练 3.6(2019 全国 I 理 18 )
如图,直四棱柱 ABCD ? ?
A1 B 1 C 1 D1 的底面是菱形, AA1 = 4 , AB = 2 , ∠ BAD = 60 , E , M ,
N 分别是 BC , BB 1 , A1 D 的中点.
( I ) 证明: MN // 平面 C 1 DE ;
( II ) 求二面角 A? MA 1 ? N 的正弦值.
变式练 3.6 分析 考查知识
变式练 3.6
解答 ( I ) 连结 B 1 C, ME ,因为 M , E 分别为 BB 1 , BC 的中点,
所以 1
ME // B 1 C ,且 ME = B 1 C .
2
又因为 N 为 A1 D 的中点,
所以 1
ND = A1 D.
2
由题设知 A1 B 1 // DC 且 A1 B 1 = DC ,
可得 B 1 C // A1 D 且 B 1 C = A1 D,
故 ME // ND 且 ME = ND ,因此四边形 MNDE 为平
行四边形, MN // ED .
又 MN ?? 平面 C 1 DE ,所以 MN // 平面 C 1 DE .
# ?
( II ) 由已知可得 DE ⊥ DA.以 D 为坐标原点, DA 的方向为
x 轴正方向,建立如图所示的空间直角坐标系 D? xyz ,
则 √
# ?
A(2 ,0 ,0) , A1 (2 ,0 ,4) , M 1 , 3 ,2 , N (1 ,0 ,2) , A1 A=
# ? √
# ?
(0 ,0 ,? 4) , A1 M = ? 1 , 3 ,? 2 , A1 N = ( ? 1 ,0 ,? 2) ,
# ? √
MN = 0 ,? 3 ,0 .
#?
设
m = ( x, y, z ) 为 平 面 A1 MA 的 法 向 量, 则
#? # ?
m · A1 M = 0 ?
#? # ?
m · A1 A= 0 .
√
? x + 3 y ? 2 z = 0 ? √
#?
所以 可取 m = 3 ,1 ,0 .
? 4 z = 0 .
#?
设 n = ( p, q, r ) 为平面 A1 MN 的法向量,
第 74 页 共 99 页
#? # ?
n · MN = 0 ? √
?
# ? 3 q = 0 ?
#?
则
#?n · ?
A .所以
1 N = 0 . ,可取 n = (2 ,0 ,
同课章节目录
