高二第二学期月考卷（数学）

高二第二学期数学月考卷
(时间：120分钟，满分：150分)
一、选择题(本大题共12个小题，在每小题所给四个选项中，只有一个是符合题目要求的)
1．y＝的定义域为(　　)
A．[2kπ－，2kπ＋](k∈Z)
B．[2kπ，2kπ＋](k∈Z)
C．[2kπ，2kπ＋π](k∈Z)
D．R
2．已知f(x)是以π为周期的偶函数，且x∈[0，]时，f(x)＝1－sinx，则当x∈[π，3π]时，f(x)等于(　　)
A．1＋sinx　　　　　　　　 B．1－sinx
C．－1－sinx D．－1＋sinx
3．设0≤x≤2π，且＝sinx－cosx，则(　　)
A．0≤x≤π　　　　　　　　 B.≤x≤π
C.≤x≤π D.≤x≤π
4．函数f(x)的部分图象如图所示，则函数的解析式为(　　)
A．f(x)＝x＋sinx
B．f(x)＝
C．f(x)＝xcosx
D．f(x)＝x(x－)(x－)
5．若A、B、C为△ABC的三个内角，则下列等式成立的是(　　)
A．sin(B＋C)＝sinA
B．cos(B＋C)＝cosA
C．tan(B＋C)＝tanA
D．cot(B＋C)＝cotA
6．若f(x)＝3sin(ωx＋φ)对任意x都有f(x＋)＝f(－x)，则f()等于(　　)
A．3或0 B．－3或3
C．0 D．－3或0
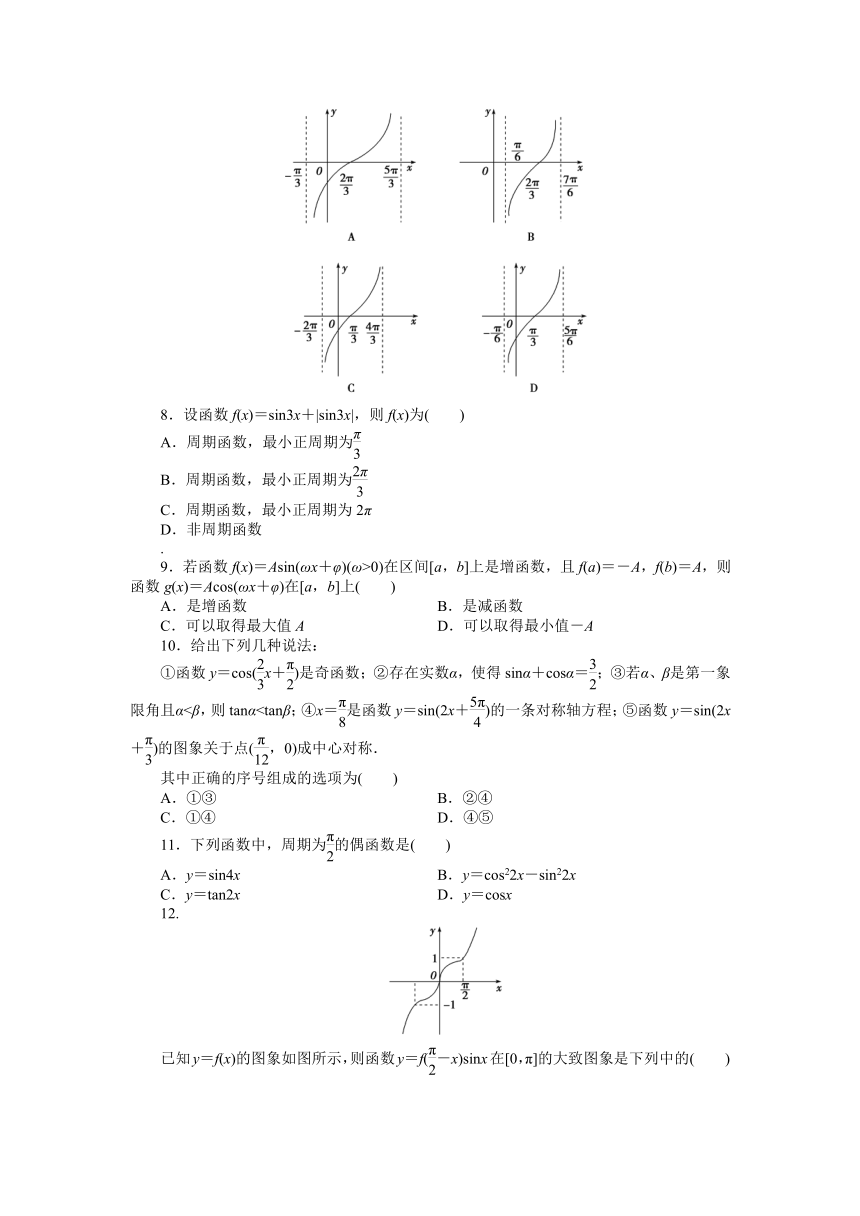
7．函数y＝tan(－)在一个周期内的图象是(　　)
8．设函数f(x)＝sin3x＋|sin3x|，则f(x)为(　　)
A．周期函数，最小正周期为
B．周期函数，最小正周期为
C．周期函数，最小正周期为2π
D．非周期函数
.
9．若函数f(x)＝Asin(ωx＋φ)(ω>0)在区间[a，b]上是增函数，且f(a)＝－A，f(b)＝A，则函数g(x)＝Acos(ωx＋φ)在[a，b]上(　　)
A．是增函数 B．是减函数
C．可以取得最大值A D．可以取得最小值－A
10．给出下列几种说法：
①函数y＝cos(x＋)是奇函数；②存在实数α，使得sinα＋cosα＝；③若α、β是第一象限角且α<β，则tanα其中正确的序号组成的选项为(　　)
A．①③　　　　　　　　 B．②④
C．①④ D．④⑤
11．下列函数中，周期为的偶函数是(　　)
A．y＝sin4x B．y＝cos22x－sin22x
C．y＝tan2x D．y＝cosx
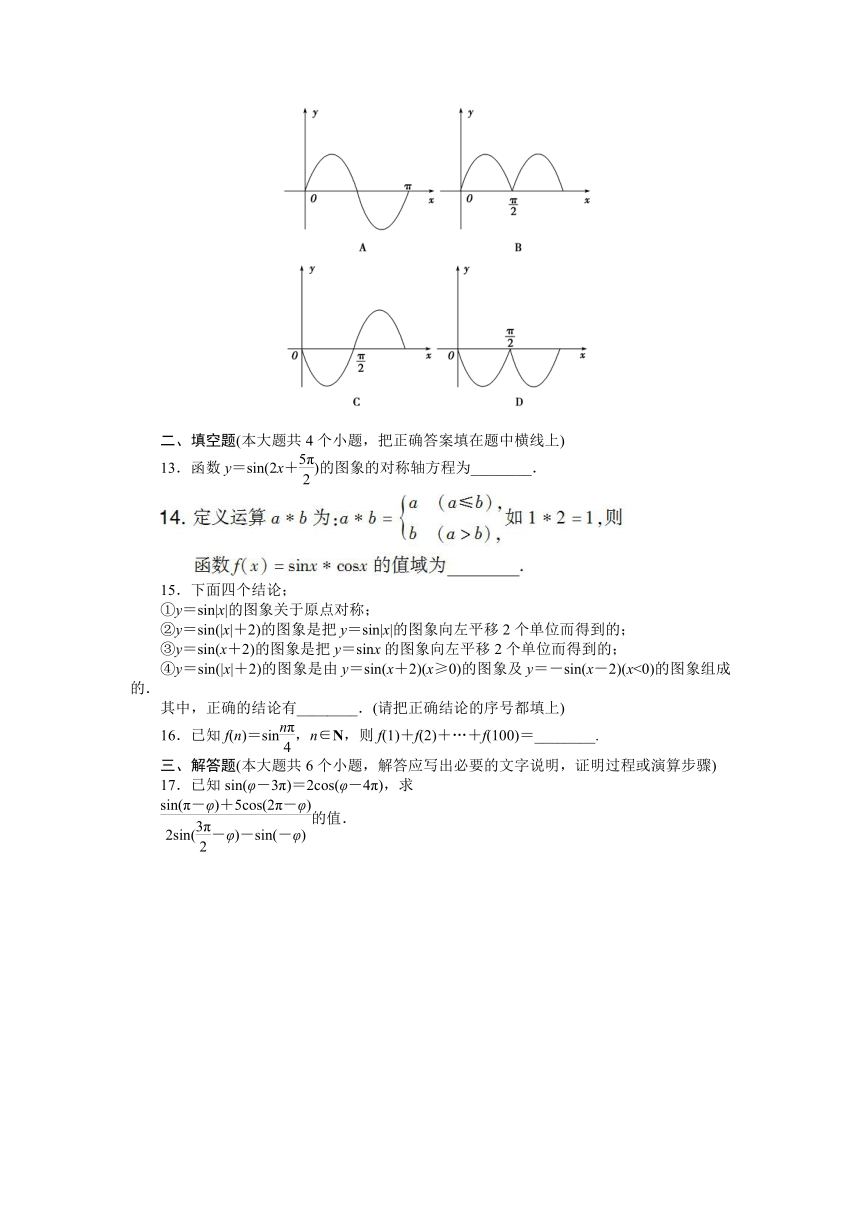
12.
已知y＝f(x)的图象如图所示，则函数y＝f(－x)sinx在[0，π]的大致图象是下列中的(　　)
二、填空题(本大题共4个小题，把正确答案填在题中横线上)
13．函数y＝sin(2x＋)的图象的对称轴方程为________．
15．下面四个结论；
①y＝sin|x|的图象关于原点对称；
②y＝sin(|x|＋2)的图象是把y＝sin|x|的图象向左平移2个单位而得到的；
③y＝sin(x＋2)的图象是把y＝sinx的图象向左平移2个单位而得到的；
④y＝sin(|x|＋2)的图象是由y＝sin(x＋2)(x≥0)的图象及y＝－sin(x－2)(x<0)的图象组成的．
其中，正确的结论有________．(请把正确结论的序号都填上)
16．已知f(n)＝sin，n∈N，则f(1)＋f(2)＋…＋f(100)＝________.
三、解答题(本大题共6个小题，解答应写出必要的文字说明，证明过程或演算步骤)
17．已知sin(φ－3π)＝2cos(φ－4π)，求
的值．
18．函数y＝Asin(ωx＋φ)(A>0，ω>0，|φ|<)在x∈(0,7π)内取到一个最大值和一个最小值，且当x＝π时，y有最大值3，当x＝6π时，y有最小值－3.
(1)求此函数解析式；
(2)写出该函数的单调递增区间．
19．(1)求函数y＝1－2sin(x＋)的最大值与最小值及相应x的值；
(2)已知函数y＝acos(2x＋)＋3，x∈[0，]的最大值为4，求实数a的值．
20．求下列函数的值域：
(1)y＝；(2)y＝acosx＋b.
21．已知f(α)＝.
(1)化简f(α)；
(2)若f(α)＝，且<α<，求cosα－sinα的值；
(3)若α＝－π，求f(α)的值．
22．如图，是函数y＝Asin(ωx＋φ)＋k(A>0，ω>0，|φ|<)的一段图象．
(1)求此函数解析式；
(2)分析一下该函数是如何通过y＝sinx变换得来的？
答案：
1. D
2. 解析：选B.当x∈[π，3π]时，
x－3π∈[－，0]，
则f(x)＝f(x－3π)＝f(3π－x)
＝1－sin(3π－x)＝1－sinx.
3.解析：选C.利用特例法或代入检验．
∵＝
＝sinx－cosx，
∴sinx≥cosx，
∵0≤x≤2π，
由单位圆中的三角函数线，可知≤x≤π.
4.解析：选C.由f(－)＝0，排除A、D；由|f()|<|f(π)|，排除B.
5. 答案：A
6. 解析：选B.由f(x＋)＝f(－x)得，f(＋x)＝f(－x)，知x＝是f(x)的对称轴．
7. 解析：选A.由kπ－<－8. 解析：选B.f(x)＝sin3x＋|sin3x|
＝
9. 解析：选C.f(b)>f(a) A>－A A>0，
f(a)＝－A ωa＋φ＝2kπ－(k∈Z)，
f(b)＝A ωb＋φ＝2kπ＋(k∈Z)，
∴g(a)＝g(b)＝0，
g()＝Acos(ω·＋φ)
＝Acos[(ωa＋φ)＋(ωb＋φ)]
＝Acos[(2kπ－)＋(2kπ＋)]
＝Acos2kπ＝A.
10. 答案：C
11. 解析：选B.A.y＝sin4x的周期为，但是奇函数．C.y＝tan2x，也是奇函数，D.y＝cosx的周期为2π.
12. 解析：选A.取特殊值x＝，x＝π，代入验证．
13. 解析：y＝sin(2x＋)＝cos2x，故对称轴为2x＝kπ，k∈Z，∴x＝(k∈Z)．
答案：x＝(k∈Z)
14. 答案：[－1，]
15. 解析：①中y＝sin|x|的图象关于y轴对称，因此①不正确；
②中y＝sin|x|的图象向左平移2个单位得到y＝sin|x＋2|的图象，而不是得到y＝sin(|x|＋2)的图象，故②不正确；
③正确；
④y＝sin(|x|＋2)＝
＝，故正确．
答案：③④
16. 解析：f(1)＝，f(2)＝1，f(3)＝，f(4)＝0，f(5)＝－，f(6)＝－1，f(7)＝－，f(8)＝0，f(9)＝f(1)＝，故f(n)是以8为周期的函数，
∴f(1)＋f(2)＋…＋f(100)＝12×0＋＋1＋＋0＝1＋.
答案：＋1
17. 解：因为sin(φ－3π)＝2cos(φ－4π)，
即－sin(3π－φ)＝2cos(4π－φ)，
即－sin(π－φ)＝2cos(－φ)，
得sinφ＝－2cosφ且sinφ≠0，cosφ≠0.
所以原式＝＝
＝＝－.
18. 解：(1)∵A＝3，＝5π，
∴T＝10π，
∴ω＝＝，＋φ＝ φ＝，
∴y＝3sin(x＋)．
(2)令2kπ－≤x＋≤2kπ＋，k∈Z，
得10kπ－4π≤x≤10kπ＋π，k∈Z.
∴函数的单调递增区间为
{x|10kπ－4π≤x≤10kπ＋π，k∈Z}．
19. 解：(1)当sin(x＋)＝－1，即x＋＝－＋2kπ，k∈Z，即x＝－＋2kπ，k∈Z时，y取得最大值1＋2＝3.
当sin(x＋)＝1，即x＋＝＋2kπ，k∈Z，即当x＝＋2kπ，k∈Z时，
y取得最小值1－2＝－1.
(2)∵x∈[0，]，∴2x＋∈[，]，
∴－1≤cos(2x＋)≤.
当a>0，cos(2x＋)＝时，
y取得最大值a＋3，
∴a＋3＝4，∴a＝2.
当a<0，cos(2x＋)＝－1时，
y取得最大值－a＋3，
∴－a＋3＝4，∴a＝－1，
综上可知，实数a的值为2或－1.
20. 解：(1)由y＝，解得sinx＝.
由于－1由－1<得＋1>0.
∴>0，
∴1－y>0，y<1.①
由≤1得
－1≤0，≤0，即≥0.
∴y>1或y≤0.②
由①②求交集得y≤0，∴值域为(－∞，0]．
(2)∵任意x∈R，有－1≤cosx≤1，
∴当a>0时，－a＋b≤acosx＋b≤a＋b；
当a<0时，a＋b≤acosx＋b≤－a＋b；
当a＝0时，acosx＋b＝b.
故当a≥0时，值域为{y|b－a≤y≤b＋a}；
当a<0时，值域为{y|a＋b≤y≤b－a}．
21. 解：(1)f(α)＝＝sinα·cosα.
(2)由f(α)＝sinαcosα＝可知，
(cosα－sinα)2＝cos2α－2sinαcosα＋sin2α
＝1－2sinαcosα＝1－2×＝.
又∵<α<，∴cosα∴cosα－sinα＝－.
(3)∵α＝－＝－6×2π＋，
∴f(－)＝cos(－)·sin(－)
＝cos(－6×2π＋)·sin(－6×2π＋)
＝cos·sin
＝cos(2π－)·sin(2π－)
＝cos·(－sin)
＝·(－)＝－.
22.解：(1)由图象知A＝＝，
k＝＝－1，
T＝2×(－)＝π，∴ω＝＝2.
∴y＝sin(2x＋φ)－1.
当x＝时，2×＋φ＝，∴φ＝.
∴所求函数解析式为y＝sin(2x＋)－1.
(2)把y＝sinx向左平移个单位，得到y＝sin(x＋)，然后纵坐标保持不变、横坐标缩短到原来的，得到y＝sin(2x＋)，再横坐标保持不变，纵坐标缩短到原来的得到y＝sin(2x＋)，最后把函数y＝sin(2x＋)的图象向下平移1个单位，得到y＝sin(2x＋)－1的图象．