【浙江省】18年到20年高考数学真题汇编(难度系数0.65以上)(含解析)
文档属性
| 名称 | 【浙江省】18年到20年高考数学真题汇编(难度系数0.65以上)(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-01 11:43:47 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
浙江18年到20年真题汇编(难度系数0.65以上)
一、单选题
1.某几何体的三视图(单位:cm)如图所示,则该几何体的体积(单位:cm3)是(
)
A.
B.
C.3
D.6
【详解】
由三视图可知,该几何体是上半部分是三棱锥,下半部分是三棱柱,
且三棱锥的一个侧面垂直于底面,且棱锥的高为1,
棱柱的底面为等腰直角三角形,棱柱的高为2,
所以几何体的体积为:
.
故选:A
2.已知空间中不过同一点的三条直线m,n,l,则“m,n,l在同一平面”是“m,n,l两两相交”的(
)
A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分也不必要条件
【详解】
依题意是空间不过同一点的三条直线,
当在同一平面时,可能,故不能得出两两相交.
当两两相交时,设,根据公理可知确定一个平面,而,根据公理可知,直线即,所以在同一平面.
综上所述,“在同一平面”是“两两相交”的必要不充分条件.
故选:B
3.函数y=xcosx+sinx在区间[–π,π]的图象大致为(
)
A.
B.
C.
D.
【详解】
因为,则,
即题中所给的函数为奇函数,函数图象关于坐标原点对称,
据此可知选项CD错误;
且时,,据此可知选项B错误.
故选:A.
4.设,则随机变量的分布列是:
则当在内增大时
A.增大
B.减小
C.先增大后减小
D.先减小后增大
【详解】
方法1:由分布列得,则
,则当在内增大时,先减小后增大.
方法2:则
故选D.
5.渐近线方程为的双曲线的离心率是
A.
B.1
C.
D.2
【详解】
根据渐近线方程为x±y=0的双曲线,可得,所以c
则该双曲线的离心率为
e,
故选C.
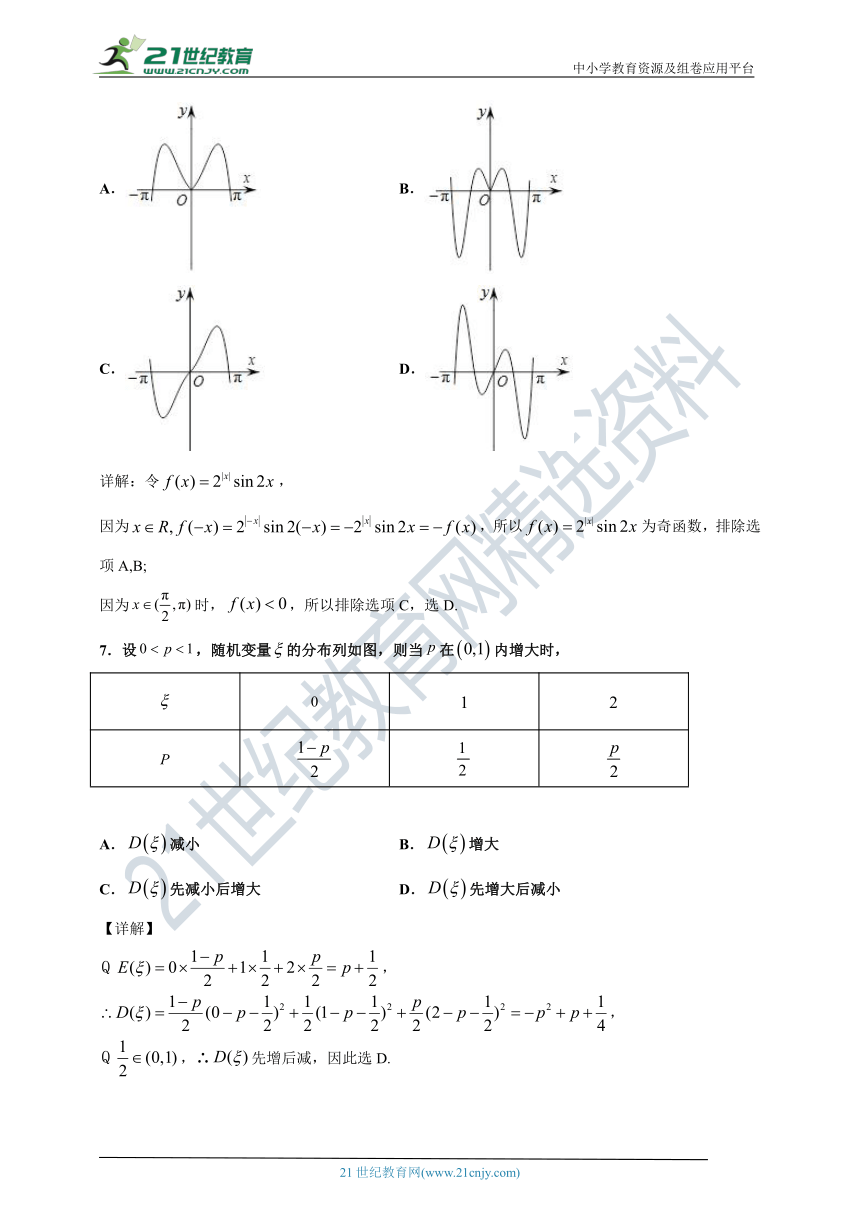
6.函数y=sin2x的图象可能是
A.
B.
C.
D.
详解:令,
因为,所以为奇函数,排除选项A,B;
因为时,,所以排除选项C,选D.
7.设,随机变量的分布列如图,则当在内增大时,
A.减小
B.增大
C.先减小后增大
D.先增大后减小
【详解】
,
,
,∴先增后减,因此选D.
8.某几何体的三视图如图所示(单位:),则该几何体的体积(单位:)是(
)
A.
B.
C.
D.
【详解】
根据三视图可得几何体为一个直四棱柱,高为,底面为直角梯形,上下底分别为、,梯形的高为,因此几何体的体积为,选C.
二、填空题
9.从1,3,5,7,9中任取2个数字,从0,2,4,6中任取2个数字,一共可以组成___________个没有重复数字的四位数.(用数字作答)
【详解】
分析:按是否取零分类讨论,若取零,则先排首位,最后根据分类与分步计数原理计数.
详解:若不取零,则排列数为若取零,则排列数为
因此一共有个没有重复数字的四位数.
10.二项式的展开式的常数项是___________.
详解:二项式的展开式的通项公式为,
令得,故所求的常数项为
三、双空题
11.设直线与圆和圆均相切,则_______;b=______.
【详解】
设,,由题意,到直线的距离等于半径,即,,
所以,所以(舍)或者,
解得.
故答案为:
12.盒子里有4个球,其中1个红球,1个绿球,2个黄球,从盒中随机取球,每次取1个,不放回,直到取出红球为止.设此过程中取到黄球的个数为,则_______;______.
【详解】
因为对应事件为第一次拿红球或第一次拿绿球,第二次拿红球,
所以,
随机变量,
,
,
所以.
故答案为:.
13.设,则________;________.
【答案】
【详解】
的通项为,
令,则,故;
.
故答案为:;.
14.已知,则________;______.
【详解】
,
,
故答案为:
15.在中,,,,点在线段上,若,则____;________.
【详解】
在中,正弦定理有:,而,
,,所以.
16.已知圆的圆心坐标是,半径长是.若直线与圆相切于点,则_____,______.
【详解】
可知,把代入得,此时.
17.在△ABC中,角A,B,C所对的边分别为a,b,c.若,b=2,A=60°,则sin
B=___________,c=___________.
详解:由正弦定理得,所以
由余弦定理得(负值舍去).
18.已知λ∈R,函数f(x)=,当λ=2时,不等式f(x)<0的解集是___________.若函数f(x)恰有2个零点,则λ的取值范围是___________.
详解:由题意得或,所以或,即,不等式f(x)<0的解集是
当时,,此时,即在上有两个零点;当时,,由在上只能有一个零点得.综上,的取值范围为.
四、解答题
19.在锐角△ABC中,角A,B,C的对边分别为a,b,c,且.
(I)求角B的大小;
(II)求cosA+cosB+cosC的取值范围.
【答案】(I);(II)
【详解】
(I)由结合正弦定理可得:
△ABC为锐角三角形,故.
(II)结合(1)的结论有:
.
由可得:,,
则,.
即的取值范围是.
20.设等差数列的前项和为,,,数列满足:对每成等比数列.
(1)求数列的通项公式;
(2)记
证明:
【详解】
(1)由题意可得:,解得:,
则数列的通项公式为
.
其前n项和.
则成等比数列,即:
,
据此有:
,
故.
(2)结合(1)中的通项公式可得:
,
则.
21.设函数.
(1)已知函数是偶函数,求的值;
(2)求函数
的值域.
【详解】
(1)由题意结合函数的解析式可得:,
函数为偶函数,则当时,,即,结合可取,相应的值为.
(2)由函数的解析式可得:
.
据此可得函数的值域为:.
22.已知角α的顶点与原点O重合,始边与x轴的非负半轴重合,它的终边过点P().
(Ⅰ)求sin(α+π)的值;
(Ⅱ)若角β满足sin(α+β)=,求cosβ的值.
详解:(Ⅰ)由角的终边过点得,
所以.
(Ⅱ)由角的终边过点得,
由得.
由得,
所以或.
23.已知等比数列{an}的公比q>1,且a3+a4+a5=28,a4+2是a3,a5的等差中项.数列{bn}满足b1=1,数列{(bn+1?bn)an}的前n项和为2n2+n.
(Ⅰ)求q的值;
(Ⅱ)求数列{bn}的通项公式.
详解:(Ⅰ)由是的等差中项得,
所以,
解得.
由得,
因为,所以.
(Ⅱ)设,数列前n项和为.
由解得.
由(Ⅰ)可知,
所以,
故,
.
设,
所以,
因此,
又,所以.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
浙江18年到20年真题汇编(难度系数0.65以上)
一、单选题
1.某几何体的三视图(单位:cm)如图所示,则该几何体的体积(单位:cm3)是(
)
A.
B.
C.3
D.6
【详解】
由三视图可知,该几何体是上半部分是三棱锥,下半部分是三棱柱,
且三棱锥的一个侧面垂直于底面,且棱锥的高为1,
棱柱的底面为等腰直角三角形,棱柱的高为2,
所以几何体的体积为:
.
故选:A
2.已知空间中不过同一点的三条直线m,n,l,则“m,n,l在同一平面”是“m,n,l两两相交”的(
)
A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分也不必要条件
【详解】
依题意是空间不过同一点的三条直线,
当在同一平面时,可能,故不能得出两两相交.
当两两相交时,设,根据公理可知确定一个平面,而,根据公理可知,直线即,所以在同一平面.
综上所述,“在同一平面”是“两两相交”的必要不充分条件.
故选:B
3.函数y=xcosx+sinx在区间[–π,π]的图象大致为(
)
A.
B.
C.
D.
【详解】
因为,则,
即题中所给的函数为奇函数,函数图象关于坐标原点对称,
据此可知选项CD错误;
且时,,据此可知选项B错误.
故选:A.
4.设,则随机变量的分布列是:
则当在内增大时
A.增大
B.减小
C.先增大后减小
D.先减小后增大
【详解】
方法1:由分布列得,则
,则当在内增大时,先减小后增大.
方法2:则
故选D.
5.渐近线方程为的双曲线的离心率是
A.
B.1
C.
D.2
【详解】
根据渐近线方程为x±y=0的双曲线,可得,所以c
则该双曲线的离心率为
e,
故选C.
6.函数y=sin2x的图象可能是
A.
B.
C.
D.
详解:令,
因为,所以为奇函数,排除选项A,B;
因为时,,所以排除选项C,选D.
7.设,随机变量的分布列如图,则当在内增大时,
A.减小
B.增大
C.先减小后增大
D.先增大后减小
【详解】
,
,
,∴先增后减,因此选D.
8.某几何体的三视图如图所示(单位:),则该几何体的体积(单位:)是(
)
A.
B.
C.
D.
【详解】
根据三视图可得几何体为一个直四棱柱,高为,底面为直角梯形,上下底分别为、,梯形的高为,因此几何体的体积为,选C.
二、填空题
9.从1,3,5,7,9中任取2个数字,从0,2,4,6中任取2个数字,一共可以组成___________个没有重复数字的四位数.(用数字作答)
【详解】
分析:按是否取零分类讨论,若取零,则先排首位,最后根据分类与分步计数原理计数.
详解:若不取零,则排列数为若取零,则排列数为
因此一共有个没有重复数字的四位数.
10.二项式的展开式的常数项是___________.
详解:二项式的展开式的通项公式为,
令得,故所求的常数项为
三、双空题
11.设直线与圆和圆均相切,则_______;b=______.
【详解】
设,,由题意,到直线的距离等于半径,即,,
所以,所以(舍)或者,
解得.
故答案为:
12.盒子里有4个球,其中1个红球,1个绿球,2个黄球,从盒中随机取球,每次取1个,不放回,直到取出红球为止.设此过程中取到黄球的个数为,则_______;______.
【详解】
因为对应事件为第一次拿红球或第一次拿绿球,第二次拿红球,
所以,
随机变量,
,
,
所以.
故答案为:.
13.设,则________;________.
【答案】
【详解】
的通项为,
令,则,故;
.
故答案为:;.
14.已知,则________;______.
【详解】
,
,
故答案为:
15.在中,,,,点在线段上,若,则____;________.
【详解】
在中,正弦定理有:,而,
,,所以.
16.已知圆的圆心坐标是,半径长是.若直线与圆相切于点,则_____,______.
【详解】
可知,把代入得,此时.
17.在△ABC中,角A,B,C所对的边分别为a,b,c.若,b=2,A=60°,则sin
B=___________,c=___________.
详解:由正弦定理得,所以
由余弦定理得(负值舍去).
18.已知λ∈R,函数f(x)=,当λ=2时,不等式f(x)<0的解集是___________.若函数f(x)恰有2个零点,则λ的取值范围是___________.
详解:由题意得或,所以或,即,不等式f(x)<0的解集是
当时,,此时,即在上有两个零点;当时,,由在上只能有一个零点得.综上,的取值范围为.
四、解答题
19.在锐角△ABC中,角A,B,C的对边分别为a,b,c,且.
(I)求角B的大小;
(II)求cosA+cosB+cosC的取值范围.
【答案】(I);(II)
【详解】
(I)由结合正弦定理可得:
△ABC为锐角三角形,故.
(II)结合(1)的结论有:
.
由可得:,,
则,.
即的取值范围是.
20.设等差数列的前项和为,,,数列满足:对每成等比数列.
(1)求数列的通项公式;
(2)记
证明:
【详解】
(1)由题意可得:,解得:,
则数列的通项公式为
.
其前n项和.
则成等比数列,即:
,
据此有:
,
故.
(2)结合(1)中的通项公式可得:
,
则.
21.设函数.
(1)已知函数是偶函数,求的值;
(2)求函数
的值域.
【详解】
(1)由题意结合函数的解析式可得:,
函数为偶函数,则当时,,即,结合可取,相应的值为.
(2)由函数的解析式可得:
.
据此可得函数的值域为:.
22.已知角α的顶点与原点O重合,始边与x轴的非负半轴重合,它的终边过点P().
(Ⅰ)求sin(α+π)的值;
(Ⅱ)若角β满足sin(α+β)=,求cosβ的值.
详解:(Ⅰ)由角的终边过点得,
所以.
(Ⅱ)由角的终边过点得,
由得.
由得,
所以或.
23.已知等比数列{an}的公比q>1,且a3+a4+a5=28,a4+2是a3,a5的等差中项.数列{bn}满足b1=1,数列{(bn+1?bn)an}的前n项和为2n2+n.
(Ⅰ)求q的值;
(Ⅱ)求数列{bn}的通项公式.
详解:(Ⅰ)由是的等差中项得,
所以,
解得.
由得,
因为,所以.
(Ⅱ)设,数列前n项和为.
由解得.
由(Ⅰ)可知,
所以,
故,
.
设,
所以,
因此,
又,所以.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
