2012届高三数学第二轮复习专题:数列的题型与方法(文科)
文档属性
| 名称 | 2012届高三数学第二轮复习专题:数列的题型与方法(文科) |  | |
| 格式 | zip | ||
| 文件大小 | 329.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-05 21:06:33 | ||
图片预览




文档简介
专题二:数列的题型与方法(文科)
考点回顾
1.数列的概念,数列的通项公式与递推关系式,等差数列和等比数列的概念、有关公式和性质。
2.判断和证明数列是等差(等比)数列常有三种方法:
(1)定义法:对于n≥2的任意自然数,验证为同一常数。
(2)通项公式法:
①若,则为等差数列;
②若,则为等比数列;
③中项公式法:验证都成立。
3.在等差数列中,有关Sn的最值问题——常用邻项变号法求解:
(1)当,d<0时,满足的项数m使得取最大值.
(2)当,d>0时,满足的项数m使得取最小值。
在解含绝对值的数列最值问题时,注意转化思想的应用。
4.数列求和的常用方法:公式法、裂项相消法、错位相减法、倒序相加法、分组求和法、累加累积法、归纳猜想证明法等。
5.数列的综合应用:
⑴函数思想、方程思想、分类讨论等思想在解决数列综合问题时常常用到。
⑵数列与函数、数列与不等式的综合、用数列知识解决实际问题等内容。
6.注意事项:
⑴证明数列是等差或等比数列常用定义,即通过证明或而得。
⑵在解决等差数列或等比数列的相关问题时,“基本量法”是常用的方法,但有时灵活地运用性质,可使运算简便。
⑶对于一般数列的问题常转化为等差、等比数列求解。
⑷注意一些特殊数列的求和方法。
⑸注意与之间关系的转化。如:
=,=.
⑹数列的综合题形式多样,解题思路灵活,但万变不离其宗,就是离不开数列的概念和性质,离不开数学思想方法,只要能把握这两方面,就会迅速打通解题思路.
⑺解综合题的成败在于审清题目,弄懂来龙去脉,透过给定信息的表象,抓住问题的本质,揭示问题的内在联系和隐含条件,明确解题方向,形成解题策略.
⑻通过解题后的反思,找准自己的问题,总结成功的经验,吸取失败的教训,增强解综合题的信心和勇气,提高分析问题和解决问题的能力.
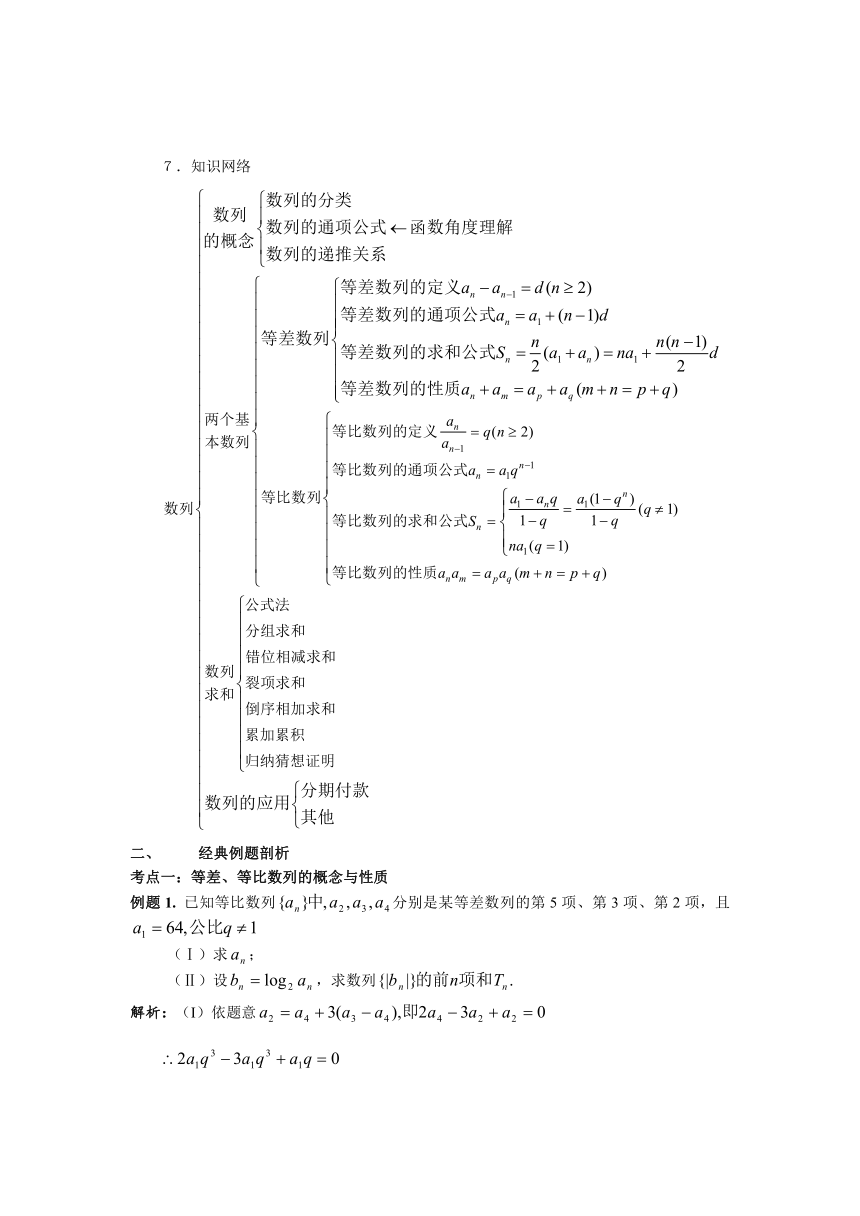
7.知识网络
经典例题剖析
考点一:等差、等比数列的概念与性质
例题1. 已知等比数列分别是某等差数列的第5项、第3项、第2项,且
(Ⅰ)求;
(Ⅱ)设,求数列
解析:(I)依题意
(II)
点评:本题考查了等比数列的基本性质和等差数列的求和,本题还考查了转化的思想。
例题2. 设数列的前n项和为Sn,若是首项为1,各项均为正数且公比为q的等比数列.
(1)求数列的通项公式;
(2)试比较的大小,并证明你的结论.
解析:(Ⅰ)∵是各项均为正数的等比数列.
∴. 当n=1时,a1=1, 当
∴。
(Ⅱ)当n=1时,
∴
∴当
∵
①当q=1时,
②当
③当
综上可知: 当n=1时,
当
若
若
点评:本题考查了等比数列的基本知识,还要注意分类讨论。
考点二:求数列的通项与求和
例题3. 已知数列中各项为:
12、1122、111222、……、 ……
(1)证明这个数列中的每一项都是两个相邻整数的积.
(2)求这个数列前n项之和Sn .
解析:先要通过观察,找出所给的一列数的特征,求出数列的通项,进一步再求和。
答案:(1)
记:A = , 则A=为整数
= A (A+1) , 得证
(2)
点评:本题难点在于求出数列的通项,再将这个通项“分成” 两个相邻正数的积,解决此题需要一定的观察能力和逻辑推理能力。
例题4. 已知是数列{}的前n项和,并且=1,对任意正整数n,;设).
(I)证明数列是等比数列,并求的通项公式;
(II)设的前n项和,求.
解析:(I)
两式相减:
是以2为公比的等比数列,
(II)
而
点评:本题利用转化思想将递推关系式转化成我们熟悉的结构求得数列的通项,第二问求和用到裂项的办法求和。
考点三:数列与不等式的联系
例题5.已知为锐角,且,
函数,数列{an}的首项.
⑴ 求函数的表达式;
⑵ 求证:;
⑶ 求证:
解析:本题是借助函数给出递推关系,第(2)问的不等式利用了函数的性质,第(3)问是转化成可以裂项的形式,这是证明数列中的不等式的另一种出路。
答案:解:⑴ 又∵为锐角
∴ ∴
⑵ ∵ ∴都大于0
∴ ∴
⑶
∴
∴
∵, , 又∵
∴ ∴
∴
点评:把复杂的问题转化成清晰的问题是数学中的重要思想,本题中的第(3)问不等式所给的式子更具有一般性。
例题6.已知数列满足且
(Ⅰ)求的表达式;
(Ⅱ)求;
(Ⅲ)若,试比较的大小,并说明理由.
解析:(I)
当时上式也成立,
(Ⅱ)
①
②
①—②,得
(Ⅲ)由(Ⅱ)可得又
当
当
当
综上所述,当
点评:比较大小的常见的办法是做差,但关键在于和零比较,要注意在不同的条件下有不同的结果,也就是要根据分类讨论。
例题7.已知函数,数列满足,
; 数列满足, .求证:
(Ⅰ)
(Ⅱ)
(Ⅲ)若则当n≥2时,.
解析:第(1)问是和自然数有关的命题,可考虑用数学归纳法证明;第(2)问可利用函数的单调性;第(3)问进行放缩。
答案:解: (Ⅰ)先用数学归纳法证明,.
(1)当n=1时,由已知得结论成立;
(2)假设当n=k时,结论成立,即.则当n=k+1时,
因为0又f(x)在上连续,所以f(0)故当n=k+1时,结论也成立. 即对于一切正整数都成立.
又由, 得,从而.
综上可知
(Ⅱ)构造函数g(x)=-f(x)= , 0由,知g(x)在(0,1)上增函数.
又g(x)在上连续,所以g(x)>g(0)=0.
因为,所以,即>0,从而
(Ⅲ) 因为 ,所以, ,
所以 ————① ,
由(Ⅱ)知:, 所以= ,
因为, n≥2,
所以 <<=————② .
由①② 两式可知: .
点评:本题是数列、超越函数、导数的学归纳法的知识交汇题,属于难题,复习时应引起注意。
考点四:数列与函数、向量、概率等的联系
例题8.无穷数列的前n项和,并且≠.
(1)求p的值;
(2)求的通项公式;
(3)作函数,如果,证明:.
解析:(1)∵ ∴ ,且p=1,或.
若是,且p=1,则由.
∴ ,矛盾.故不可能是:,且p=1.由,得.
又,∴ .
(2)∵ ,, ∴ .
.
当k≥2时,.
∴ n≥3时有.
∴ 对一切有:.
(3)∵ , ∴ . .
故. ∴ .
又.
∴ .
故 .
点评:本题是函数、不等式的综合题,是高考的难点热点。
例题9.已知定义域为R的二次函数的最小值为0且有,直线被的图象截得的弦长为,数列满足,
(1)求函数的表达式;
(2)求证;
(3)设,求数列的最值及相应的。
解析:第(2)问实际上是求数列的通项;第(2)问利用二次函数中求最值的方式来解决。
答案:解:(1)设,则两图象交点为
∵ ∴
(2) ∵
∴
∵ ∴,故 ∴,
数列是首项为1,公差为的等差数列
∴,
(3)
令,
则 ∵
∴的值分别为
经比较距最近
当时,有最小值是,当时,有最小值是。
点评:本题二次函数、不等式知识的交汇题,要解决好这类题是要有一定的数学素养的。
例题10.某人抛掷一枚硬币,出现正面、反面的概率均为,使得
(I)求S4=2的概率;
(II)若前两次均出现正面,求的概率.
解析:解:(I)若S4=2,则需4次中有3次正面1次反面,设概率为P1,则
所以,S4=2的概率为.
(II)且前两次出现正面,则后4次中有2次正面2次反面或3次正面1次反面,设其概率为P2,则
∴若前两次均出现正面,则的概率为.
点评:本题是以数列和概率的背景出现,题型新颖而别开生面,要解决好此题要需要冷静,问题本身并不难。
三、 强化训练
(一)选择题
1.在正整数100至500之间能被11整除的个数为( )
A.34 B.35 C.36 D.37
2.在数列{an}中,a1=1,an+1=an2-1(n≥1),则a1+a2+a3+a4+a5等于( )
A.-1 B.1 C.0 D.2
3.{an}是等差数列,且a1+a4+a7=45,a2+a5+a8=39,则a3+a6+a9的值是( )
A.24 B.27 C.30 D.33
4.等差数列{an}中,已知a1=-6,an=0,公差d∈N*,则n(n≥3)的最大值为( )
A.5 B.6 C.7 D.8
5.设an=-n2+10n+11,则数列{an}从首项到第几项的和最大( )
A.第10项 B.第11项 C.第10项或11项 D.第12项
6.已知等差数列{an}的公差为正数,且a3·a7=-12,a4+a6=-4,则S20为( )
A.180 B.-180 C.90 D.-90
7.设函数f(x)满足f(n+1)=(n∈N*)且f(1)=2,则f(20)为( )
A.95 B.97 C.105 D.192
8.由公差为d的等差数列a1、a2、a3…重新组成的数列a1+a4, a2+a5, a3+a6…是( )
A.公差为d的等差数列 B.公差为2d的等差数列
C.公差为3d的等差数列 D.非等差数列
考查等差数列的性质.
9.已知三角形的三边构成等比数列,它们的公比为,
则的取值范围是( )
A. B. C. D.
10.数列的通项公式,若此数列满足(),则的取值范围是
A, B, C, D,
11.等差数列,的前项和分别为,,若,则=
A, B, C, D,
12.三个数成等比数列,且,则的取值范围是 ( )
(A) (B) (C) (D)
(二)填空题
13.在数列{an}中,a1=1,an+1=(n∈N*),则是这个数列的第_________项.
14.在等差数列{an}中,已知S100=10,S10=100,则S110=_________.
15.在-9和3之间插入n个数,使这n+2个数组成和为-21的等差数列,则n=_______.
16.等差数列{an},{bn}的前n项和分别为Sn、Tn,若=,则=_________.
(三)解答题
17.已知函数
(1)求的反函数,并指出其定义域;
(2)若数列{an}的前n项和Sn对所有的大于1的自然数n都有,且a1 =1,求数列{an}的通项公式;
(3)令
18.已知数列{an}满足
(1)求证:{an}为等比数列;
(2)记为数列{bn}的前n项和,那么:
①当a=2时,求Tn;
②当时,是否存在正整数m,使得对于任意正整数n都有如果存在,求出m的值;如果不存在,请说明理由.
19.已知数列{an}的前n项和为Sn,且
(Ⅰ)求证:数列为等差数列;
(Ⅱ)求满足的自然数n的集合.
20.已知数列为等差数列,其前n项和为
(I)若成立,并将其整合为一个等式;
(II)一般地,若存在正整数k,使,我们可将(I)中的结论作相应推广,试写出推广后的结论,并推断它是否正确.
21.已知数列满足递推式,其中
(Ⅰ)求;
(Ⅱ)求数列的通项公式;
(Ⅲ)求数列的前n项和.
22.已知等差数列,公差d大于0,且是方程的两个根,数列的前n项和为。
(1)求数列、的通项公式;
(2)记
强化训练题答案
1.【答案】C解析:观察出100至500之间能被11整除的数为110、121、132、…它们构成一个等差数列,公差为11,数an=110+(n-1)·11=11n+99,由an≤500,解得n≤36.4,n∈N*,∴n≤36.
2.【答案】A解析:由已知:an+1=an2-1=(an+1)(an-1),
∴a2=0,a3=-1,a4=0,a5=-1.
3.【答案】D解析:a1+a4+a7,a2+a5+a8,a3+a6+a9成等差数列,故a3+a6+a9=2×39-45=33.
4.【答案】C解析:an=a1+(n-1)d,即-6+(n-1)d=0n=+1
∵d∈N*,当d=1时,n取最大值n=7.
5.【答案】C解析:由an=-n2+10n+11=-(n+1)(n-11),得a11=0,而a10>0,a12<0,S10=S11.
6.【答案】A解析:由等差数列性质,a4+a6=a3+a7=-4与a3·a7=-12联立,即a3,a7是方程x2+4x-12=0的两根,又公差d>0,∴a7>a3a7=2,a3=-6,从而得a1=-10,d=2,S20=180.
7.【答案】B
解析:f(n+1)-f(n)=
相加得f(20)-f(1)=(1+2+…+19)f(20)=95+f(1)=97.
8.【答案】B 解析:(a2+a5)-(a1+a4)=(a2-a1)+(a5-a4)=2d.(a3+a6)-(a2+a5)=(a3-a2)+(a6-a5)=2d.依次类推.
9.【答案】D 解析: 设三边为则,即
得,即
10.【答案】D 解析:1由,恒成立,有,得。
11.【答案】B 解析: 2。
12.【答案】D解析:设,则有。当时,,而,;当时,,即,而,则,故。
13.【答案】6解析:由已知得=+,∴{}是以=1为首项,公差d=的等差数列.
∴=1+(n-1),∴an==,∴n=6.
14.【答案】-110解析:S100-S10=a11+a12+…+a100=45(a11+a100)=45(a1+a110)=-90a1+a110=-2.
S110=(a1+a110)×110=-110.
15.【答案】5解析:-21=,∴n=5.
16.【答案】解析:==.
17.解:(1)
定义域为:
(2)
又
而a1 = 1符合上式,故
(3)
18.解:1)当n≥2时,
整理得
所以{an}是公比为a的等比数列.(4分)
(2)
①当a=2时,
两式相减,得
(9分)
②因为-1<a<0,所以:当n为偶数时,
当n为奇数时,
所以,如果存在满足条件的正整数m,则m一定是偶数.
当
所以
所以当
当
故存在正整数m=8,使得对于任意正整数n都有
19.解:(Ⅰ)
为首项,-1为公差的等差数列.
(Ⅱ)由(Ⅰ)知,
当
由,解得,而
故所求n的集合为{6}.
20.解:(I)
;
;
∴对任意
(II)推广:设等差数列的前n项和为Sn,若存在正整数k,使
则对任意
设的公差为
故推广后的结论正确.
21.解:(1)由知
解得:同理得
(2)由知
构成以为首项以2为公比的等比数列;
;
为所求通项公式
(3)
22.解:(1)设的公差为d,由题意得:
(2)
(四)创新试题
1. 在直角坐标平面上有一点列,对一切正整数,点位于函数的图象上,且的横坐标构成以为首项, 为公差的等差数列.
⑴求点的坐标;
⑵设抛物线列中的每一条的对称轴都垂直于轴,第条抛物线的顶点为,且过点,记与抛物线相切于的直线的斜率为,求:.
2. 设数列{an}的首项a1=1,前n项和Sn满足关系式 ( http: / / www. / wxc / ) 3tSn-(2t+3)Sn-1=3t(t>0,n=2,3,4…) ( http: / / www. / wxc / )
(1)求证 ( http: / / www. / wxc / ) 数列{an}是等比数列;
(2)设数列{an}的公比为f(t),作数列{bn},使b1=1,bn=f()(n=2,3,4…),求数列{bn}的通项bn;
(3)求和 ( http: / / www. / wxc / ) b1b2-b2b3+b3b4-…+b2n-1b2n-b2nb2n+1 ( http: / / www. / wxc / )
创新试题答案
1.解:(1)
(2)的对称轴垂直于轴,且顶点为.设的方程为:
把代入上式,得,的方程为:。
,
=
2.解 ( http: / / www. / wxc / ) (1)由S1=a1=1,S2=1+a2,得3t(1+a2)-(2t+3)=3t ( http: / / www. / wxc / ) ∴a2= ( http: / / www. / wxc / )
又3tSn-(2t+3)Sn-1=3t, ①
3tSn-1-(2t+3)Sn-2=3t ②
①-②得3tan-(2t+3)an-1=0 ( http: / / www. / wxc / ) ∴,n=2,3,4…,
所以{an}是一个首项为1公比为的等比数列;
(2)由f(t)= =,得bn=f()=+bn-1? ( http: / / www. / wxc / )
可见{bn}是一个首项为1,公差为的等差数列 ( http: / / www. / wxc / ) 于是bn=1+(n-1)=;
(3)由bn=,可知{b2n-1}和{b2n}是首项分别为1和,公差均为的等差数列,
于是b2n=,
∴b1b2-b2b3+b3b4-b4b5+…+b2n-1b2n-b2nb2n+1?
=b2(b1-b3)+b4(b3-b5)+…+b2n(b2n-1-b2n+1)
=- (b2+b4+…+b2n)=-·n(+)=- (2n2+3n) ( http: / / www. / wxc / )
个
个
个
考点回顾
1.数列的概念,数列的通项公式与递推关系式,等差数列和等比数列的概念、有关公式和性质。
2.判断和证明数列是等差(等比)数列常有三种方法:
(1)定义法:对于n≥2的任意自然数,验证为同一常数。
(2)通项公式法:
①若,则为等差数列;
②若,则为等比数列;
③中项公式法:验证都成立。
3.在等差数列中,有关Sn的最值问题——常用邻项变号法求解:
(1)当,d<0时,满足的项数m使得取最大值.
(2)当,d>0时,满足的项数m使得取最小值。
在解含绝对值的数列最值问题时,注意转化思想的应用。
4.数列求和的常用方法:公式法、裂项相消法、错位相减法、倒序相加法、分组求和法、累加累积法、归纳猜想证明法等。
5.数列的综合应用:
⑴函数思想、方程思想、分类讨论等思想在解决数列综合问题时常常用到。
⑵数列与函数、数列与不等式的综合、用数列知识解决实际问题等内容。
6.注意事项:
⑴证明数列是等差或等比数列常用定义,即通过证明或而得。
⑵在解决等差数列或等比数列的相关问题时,“基本量法”是常用的方法,但有时灵活地运用性质,可使运算简便。
⑶对于一般数列的问题常转化为等差、等比数列求解。
⑷注意一些特殊数列的求和方法。
⑸注意与之间关系的转化。如:
=,=.
⑹数列的综合题形式多样,解题思路灵活,但万变不离其宗,就是离不开数列的概念和性质,离不开数学思想方法,只要能把握这两方面,就会迅速打通解题思路.
⑺解综合题的成败在于审清题目,弄懂来龙去脉,透过给定信息的表象,抓住问题的本质,揭示问题的内在联系和隐含条件,明确解题方向,形成解题策略.
⑻通过解题后的反思,找准自己的问题,总结成功的经验,吸取失败的教训,增强解综合题的信心和勇气,提高分析问题和解决问题的能力.
7.知识网络
经典例题剖析
考点一:等差、等比数列的概念与性质
例题1. 已知等比数列分别是某等差数列的第5项、第3项、第2项,且
(Ⅰ)求;
(Ⅱ)设,求数列
解析:(I)依题意
(II)
点评:本题考查了等比数列的基本性质和等差数列的求和,本题还考查了转化的思想。
例题2. 设数列的前n项和为Sn,若是首项为1,各项均为正数且公比为q的等比数列.
(1)求数列的通项公式;
(2)试比较的大小,并证明你的结论.
解析:(Ⅰ)∵是各项均为正数的等比数列.
∴. 当n=1时,a1=1, 当
∴。
(Ⅱ)当n=1时,
∴
∴当
∵
①当q=1时,
②当
③当
综上可知: 当n=1时,
当
若
若
点评:本题考查了等比数列的基本知识,还要注意分类讨论。
考点二:求数列的通项与求和
例题3. 已知数列中各项为:
12、1122、111222、……、 ……
(1)证明这个数列中的每一项都是两个相邻整数的积.
(2)求这个数列前n项之和Sn .
解析:先要通过观察,找出所给的一列数的特征,求出数列的通项,进一步再求和。
答案:(1)
记:A = , 则A=为整数
= A (A+1) , 得证
(2)
点评:本题难点在于求出数列的通项,再将这个通项“分成” 两个相邻正数的积,解决此题需要一定的观察能力和逻辑推理能力。
例题4. 已知是数列{}的前n项和,并且=1,对任意正整数n,;设).
(I)证明数列是等比数列,并求的通项公式;
(II)设的前n项和,求.
解析:(I)
两式相减:
是以2为公比的等比数列,
(II)
而
点评:本题利用转化思想将递推关系式转化成我们熟悉的结构求得数列的通项,第二问求和用到裂项的办法求和。
考点三:数列与不等式的联系
例题5.已知为锐角,且,
函数,数列{an}的首项.
⑴ 求函数的表达式;
⑵ 求证:;
⑶ 求证:
解析:本题是借助函数给出递推关系,第(2)问的不等式利用了函数的性质,第(3)问是转化成可以裂项的形式,这是证明数列中的不等式的另一种出路。
答案:解:⑴ 又∵为锐角
∴ ∴
⑵ ∵ ∴都大于0
∴ ∴
⑶
∴
∴
∵, , 又∵
∴ ∴
∴
点评:把复杂的问题转化成清晰的问题是数学中的重要思想,本题中的第(3)问不等式所给的式子更具有一般性。
例题6.已知数列满足且
(Ⅰ)求的表达式;
(Ⅱ)求;
(Ⅲ)若,试比较的大小,并说明理由.
解析:(I)
当时上式也成立,
(Ⅱ)
①
②
①—②,得
(Ⅲ)由(Ⅱ)可得又
当
当
当
综上所述,当
点评:比较大小的常见的办法是做差,但关键在于和零比较,要注意在不同的条件下有不同的结果,也就是要根据分类讨论。
例题7.已知函数,数列满足,
; 数列满足, .求证:
(Ⅰ)
(Ⅱ)
(Ⅲ)若则当n≥2时,.
解析:第(1)问是和自然数有关的命题,可考虑用数学归纳法证明;第(2)问可利用函数的单调性;第(3)问进行放缩。
答案:解: (Ⅰ)先用数学归纳法证明,.
(1)当n=1时,由已知得结论成立;
(2)假设当n=k时,结论成立,即.则当n=k+1时,
因为0
又由, 得,从而.
综上可知
(Ⅱ)构造函数g(x)=-f(x)= , 0
又g(x)在上连续,所以g(x)>g(0)=0.
因为,所以,即>0,从而
(Ⅲ) 因为 ,所以, ,
所以 ————① ,
由(Ⅱ)知:, 所以= ,
因为, n≥2,
所以 <<=————② .
由①② 两式可知: .
点评:本题是数列、超越函数、导数的学归纳法的知识交汇题,属于难题,复习时应引起注意。
考点四:数列与函数、向量、概率等的联系
例题8.无穷数列的前n项和,并且≠.
(1)求p的值;
(2)求的通项公式;
(3)作函数,如果,证明:.
解析:(1)∵ ∴ ,且p=1,或.
若是,且p=1,则由.
∴ ,矛盾.故不可能是:,且p=1.由,得.
又,∴ .
(2)∵ ,, ∴ .
.
当k≥2时,.
∴ n≥3时有.
∴ 对一切有:.
(3)∵ , ∴ . .
故. ∴ .
又.
∴ .
故 .
点评:本题是函数、不等式的综合题,是高考的难点热点。
例题9.已知定义域为R的二次函数的最小值为0且有,直线被的图象截得的弦长为,数列满足,
(1)求函数的表达式;
(2)求证;
(3)设,求数列的最值及相应的。
解析:第(2)问实际上是求数列的通项;第(2)问利用二次函数中求最值的方式来解决。
答案:解:(1)设,则两图象交点为
∵ ∴
(2) ∵
∴
∵ ∴,故 ∴,
数列是首项为1,公差为的等差数列
∴,
(3)
令,
则 ∵
∴的值分别为
经比较距最近
当时,有最小值是,当时,有最小值是。
点评:本题二次函数、不等式知识的交汇题,要解决好这类题是要有一定的数学素养的。
例题10.某人抛掷一枚硬币,出现正面、反面的概率均为,使得
(I)求S4=2的概率;
(II)若前两次均出现正面,求的概率.
解析:解:(I)若S4=2,则需4次中有3次正面1次反面,设概率为P1,则
所以,S4=2的概率为.
(II)且前两次出现正面,则后4次中有2次正面2次反面或3次正面1次反面,设其概率为P2,则
∴若前两次均出现正面,则的概率为.
点评:本题是以数列和概率的背景出现,题型新颖而别开生面,要解决好此题要需要冷静,问题本身并不难。
三、 强化训练
(一)选择题
1.在正整数100至500之间能被11整除的个数为( )
A.34 B.35 C.36 D.37
2.在数列{an}中,a1=1,an+1=an2-1(n≥1),则a1+a2+a3+a4+a5等于( )
A.-1 B.1 C.0 D.2
3.{an}是等差数列,且a1+a4+a7=45,a2+a5+a8=39,则a3+a6+a9的值是( )
A.24 B.27 C.30 D.33
4.等差数列{an}中,已知a1=-6,an=0,公差d∈N*,则n(n≥3)的最大值为( )
A.5 B.6 C.7 D.8
5.设an=-n2+10n+11,则数列{an}从首项到第几项的和最大( )
A.第10项 B.第11项 C.第10项或11项 D.第12项
6.已知等差数列{an}的公差为正数,且a3·a7=-12,a4+a6=-4,则S20为( )
A.180 B.-180 C.90 D.-90
7.设函数f(x)满足f(n+1)=(n∈N*)且f(1)=2,则f(20)为( )
A.95 B.97 C.105 D.192
8.由公差为d的等差数列a1、a2、a3…重新组成的数列a1+a4, a2+a5, a3+a6…是( )
A.公差为d的等差数列 B.公差为2d的等差数列
C.公差为3d的等差数列 D.非等差数列
考查等差数列的性质.
9.已知三角形的三边构成等比数列,它们的公比为,
则的取值范围是( )
A. B. C. D.
10.数列的通项公式,若此数列满足(),则的取值范围是
A, B, C, D,
11.等差数列,的前项和分别为,,若,则=
A, B, C, D,
12.三个数成等比数列,且,则的取值范围是 ( )
(A) (B) (C) (D)
(二)填空题
13.在数列{an}中,a1=1,an+1=(n∈N*),则是这个数列的第_________项.
14.在等差数列{an}中,已知S100=10,S10=100,则S110=_________.
15.在-9和3之间插入n个数,使这n+2个数组成和为-21的等差数列,则n=_______.
16.等差数列{an},{bn}的前n项和分别为Sn、Tn,若=,则=_________.
(三)解答题
17.已知函数
(1)求的反函数,并指出其定义域;
(2)若数列{an}的前n项和Sn对所有的大于1的自然数n都有,且a1 =1,求数列{an}的通项公式;
(3)令
18.已知数列{an}满足
(1)求证:{an}为等比数列;
(2)记为数列{bn}的前n项和,那么:
①当a=2时,求Tn;
②当时,是否存在正整数m,使得对于任意正整数n都有如果存在,求出m的值;如果不存在,请说明理由.
19.已知数列{an}的前n项和为Sn,且
(Ⅰ)求证:数列为等差数列;
(Ⅱ)求满足的自然数n的集合.
20.已知数列为等差数列,其前n项和为
(I)若成立,并将其整合为一个等式;
(II)一般地,若存在正整数k,使,我们可将(I)中的结论作相应推广,试写出推广后的结论,并推断它是否正确.
21.已知数列满足递推式,其中
(Ⅰ)求;
(Ⅱ)求数列的通项公式;
(Ⅲ)求数列的前n项和.
22.已知等差数列,公差d大于0,且是方程的两个根,数列的前n项和为。
(1)求数列、的通项公式;
(2)记
强化训练题答案
1.【答案】C解析:观察出100至500之间能被11整除的数为110、121、132、…它们构成一个等差数列,公差为11,数an=110+(n-1)·11=11n+99,由an≤500,解得n≤36.4,n∈N*,∴n≤36.
2.【答案】A解析:由已知:an+1=an2-1=(an+1)(an-1),
∴a2=0,a3=-1,a4=0,a5=-1.
3.【答案】D解析:a1+a4+a7,a2+a5+a8,a3+a6+a9成等差数列,故a3+a6+a9=2×39-45=33.
4.【答案】C解析:an=a1+(n-1)d,即-6+(n-1)d=0n=+1
∵d∈N*,当d=1时,n取最大值n=7.
5.【答案】C解析:由an=-n2+10n+11=-(n+1)(n-11),得a11=0,而a10>0,a12<0,S10=S11.
6.【答案】A解析:由等差数列性质,a4+a6=a3+a7=-4与a3·a7=-12联立,即a3,a7是方程x2+4x-12=0的两根,又公差d>0,∴a7>a3a7=2,a3=-6,从而得a1=-10,d=2,S20=180.
7.【答案】B
解析:f(n+1)-f(n)=
相加得f(20)-f(1)=(1+2+…+19)f(20)=95+f(1)=97.
8.【答案】B 解析:(a2+a5)-(a1+a4)=(a2-a1)+(a5-a4)=2d.(a3+a6)-(a2+a5)=(a3-a2)+(a6-a5)=2d.依次类推.
9.【答案】D 解析: 设三边为则,即
得,即
10.【答案】D 解析:1由,恒成立,有,得。
11.【答案】B 解析: 2。
12.【答案】D解析:设,则有。当时,,而,;当时,,即,而,则,故。
13.【答案】6解析:由已知得=+,∴{}是以=1为首项,公差d=的等差数列.
∴=1+(n-1),∴an==,∴n=6.
14.【答案】-110解析:S100-S10=a11+a12+…+a100=45(a11+a100)=45(a1+a110)=-90a1+a110=-2.
S110=(a1+a110)×110=-110.
15.【答案】5解析:-21=,∴n=5.
16.【答案】解析:==.
17.解:(1)
定义域为:
(2)
又
而a1 = 1符合上式,故
(3)
18.解:1)当n≥2时,
整理得
所以{an}是公比为a的等比数列.(4分)
(2)
①当a=2时,
两式相减,得
(9分)
②因为-1<a<0,所以:当n为偶数时,
当n为奇数时,
所以,如果存在满足条件的正整数m,则m一定是偶数.
当
所以
所以当
当
故存在正整数m=8,使得对于任意正整数n都有
19.解:(Ⅰ)
为首项,-1为公差的等差数列.
(Ⅱ)由(Ⅰ)知,
当
由,解得,而
故所求n的集合为{6}.
20.解:(I)
;
;
∴对任意
(II)推广:设等差数列的前n项和为Sn,若存在正整数k,使
则对任意
设的公差为
故推广后的结论正确.
21.解:(1)由知
解得:同理得
(2)由知
构成以为首项以2为公比的等比数列;
;
为所求通项公式
(3)
22.解:(1)设的公差为d,由题意得:
(2)
(四)创新试题
1. 在直角坐标平面上有一点列,对一切正整数,点位于函数的图象上,且的横坐标构成以为首项, 为公差的等差数列.
⑴求点的坐标;
⑵设抛物线列中的每一条的对称轴都垂直于轴,第条抛物线的顶点为,且过点,记与抛物线相切于的直线的斜率为,求:.
2. 设数列{an}的首项a1=1,前n项和Sn满足关系式 ( http: / / www. / wxc / ) 3tSn-(2t+3)Sn-1=3t(t>0,n=2,3,4…) ( http: / / www. / wxc / )
(1)求证 ( http: / / www. / wxc / ) 数列{an}是等比数列;
(2)设数列{an}的公比为f(t),作数列{bn},使b1=1,bn=f()(n=2,3,4…),求数列{bn}的通项bn;
(3)求和 ( http: / / www. / wxc / ) b1b2-b2b3+b3b4-…+b2n-1b2n-b2nb2n+1 ( http: / / www. / wxc / )
创新试题答案
1.解:(1)
(2)的对称轴垂直于轴,且顶点为.设的方程为:
把代入上式,得,的方程为:。
,
=
2.解 ( http: / / www. / wxc / ) (1)由S1=a1=1,S2=1+a2,得3t(1+a2)-(2t+3)=3t ( http: / / www. / wxc / ) ∴a2= ( http: / / www. / wxc / )
又3tSn-(2t+3)Sn-1=3t, ①
3tSn-1-(2t+3)Sn-2=3t ②
①-②得3tan-(2t+3)an-1=0 ( http: / / www. / wxc / ) ∴,n=2,3,4…,
所以{an}是一个首项为1公比为的等比数列;
(2)由f(t)= =,得bn=f()=+bn-1? ( http: / / www. / wxc / )
可见{bn}是一个首项为1,公差为的等差数列 ( http: / / www. / wxc / ) 于是bn=1+(n-1)=;
(3)由bn=,可知{b2n-1}和{b2n}是首项分别为1和,公差均为的等差数列,
于是b2n=,
∴b1b2-b2b3+b3b4-b4b5+…+b2n-1b2n-b2nb2n+1?
=b2(b1-b3)+b4(b3-b5)+…+b2n(b2n-1-b2n+1)
=- (b2+b4+…+b2n)=-·n(+)=- (2n2+3n) ( http: / / www. / wxc / )
个
个
个
同课章节目录
