2021年新高考北京卷数学高考真题(Word版,含答案)
文档属性
| 名称 | 2021年新高考北京卷数学高考真题(Word版,含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 552.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-28 09:44:18 | ||
图片预览

文档简介
2021年普通高等学校招生全国统一考试
北京卷·数学
第一部分(选择题共40分)
一、选择题共10小题,每小题4分,共40分,在每小题列出的四个选项中,选出符合题目要求的一项.
1.
已知集合,,则(
)
A.
B.
C.
D.
2.
在复平面内,复数满足,则(
)
A.
1
B.i
C.
D.
3.设函数的定义域为,则“函数在上单调递增”是“函数在上的最大值为”的(
)
A.
充分不必要条件
B.
必要不充分条件
C.
充分必要条件
D.
既不充分也不必要条件
4.
某四面体的三视图如图所示,该四面体的表面积为(
)
A.
B.
C.
D.
5.
双曲线过点,离心率为,则该双曲线的标准方程为(
)
A.
B.
C.
D.
6.已知和是两个等差数列,且是常值,若,,,则的值为(
)
A.
B.
100
C.
128
D.
132
7.已知函数,则该函数(
)
A.
奇函数,最大值为2
B.
偶函数,最大值为2
C.
奇函数,最大值为
D.
偶函数,最大值为
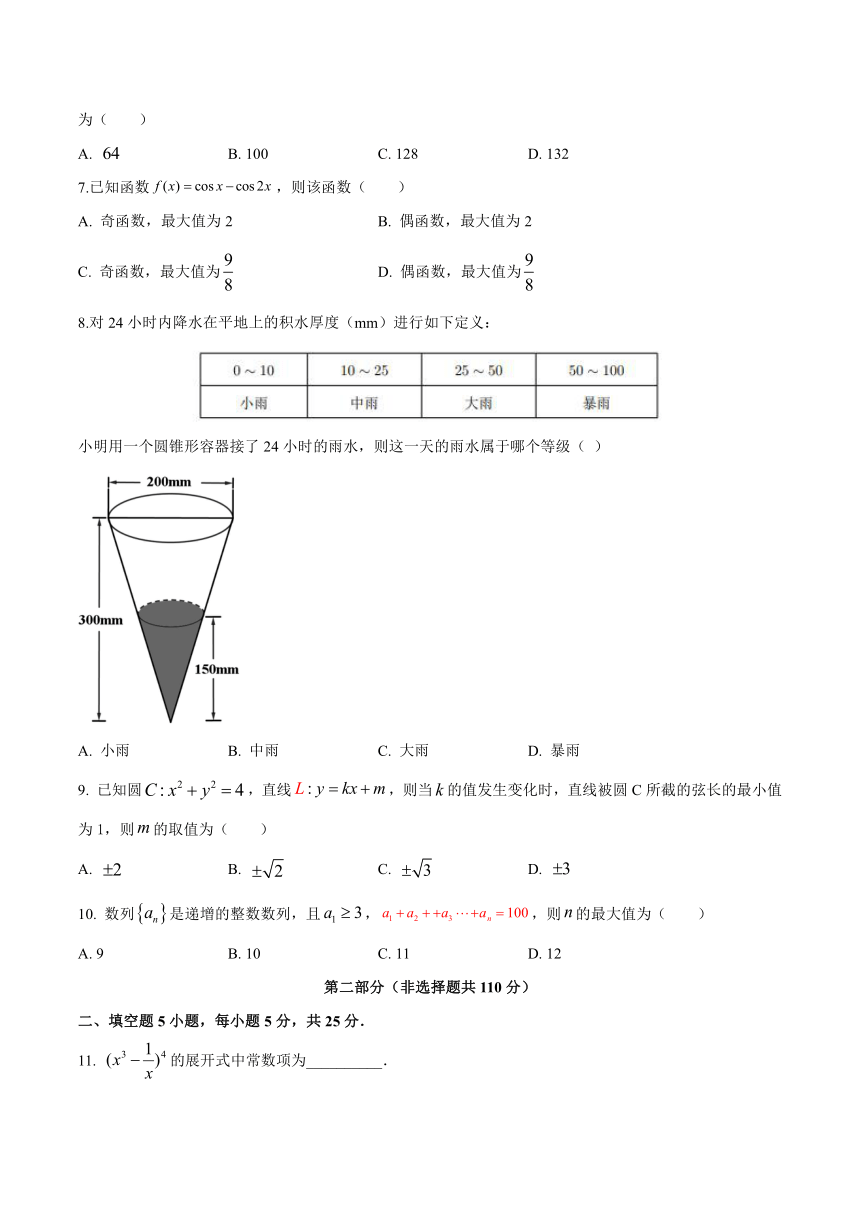
8.对24小时内降水在平地上的积水厚度(mm)进行如下定义:
小明用一个圆锥形容器接了24小时的雨水,则这一天的雨水属于哪个等级(
)
A.
小雨
B.
中雨
C.
大雨
D.
暴雨
9.
已知圆,直线,则当的值发生变化时,直线被圆C所截的弦长的最小值为1,则的取值为(
)
A.
B.
C.
D.
10.
数列是递增的整数数列,且,,则的最大值为(
)
A.
9
B.
10
C.
11
D.
12
第二部分(非选择题共110分)
二、填空题5小题,每小题5分,共25分.
11.
的展开式中常数项为__________.
12.
已知抛物线,C焦点为,点在上,且,则的横坐标是_______;作轴于,则_______.
13.
,,,则_______;_______.
14.
若点与点关于轴对称,写出一个符合题意的值___.
15.
已知,给出下列四个结论:
①若,则有两个零点;
②,使得有一个零点;
③,使得有三个零点;
④,使得有三个零点.
以上正确结论的序号是_______.
三、解答题共6小题,共85分,解答应写出文字说明,演算步骤或证明过程.
16.
已知在中,,.
(1)求的大小;
(2)在三个条件中选择一个作为已知,使存在且唯一确定,并求出边上的中线的长度.
①;②周长为;③面积为;
17.
已知正方体,点为中点,直线交平面于点.
(1)求证:点为中点;
(2)若点为棱上一点,且二面角的余弦值为,求的值.
18.
为加快新冠肺炎检测效率,某检测机构采取“k合1检测法”,即将k个人的拭子样本合并检测,若为阴性,则可确定所有样本都是阴性的;若为阳性,则还需要对本组的每个人再做检测.现有100人,已知其中2人感染病毒.
(1)①若采用“10合1检测法”,且两名患者在同一组,求总检测次数;
②已知10人分成一组,分10组,两名感染患者在同一组的概率为,定义随机变量X为总检测次数,求检测次数X的分布列和数学期望E(X);
(2)若采用“5合1检测法”,检测次数Y的期望为E(Y),试比较E(X)和E(Y)的大小(直接写出结果).
19.
已知函数.
(1)若,求在处的切线方程;
(2)若函数在处取得极值,求的单调区间,以及最大值和最小值.
20.
已知椭圆过点,以四个顶点围成的四边形面积为.
(1)求椭圆E的标准方程;
(2)过点P(0,-3)的直线l斜率为k,交椭圆E于不同的两点B,C,直线AB,AC交y=-3于点M、N,若|PM|+|PN|≤15,求k的取值范围.
21.
定义数列:对p∈R,满足:①,;②;③,.
(1)对前4项2,-2,0,1的数列,可以是数列吗?说明理由;
(2)若是数列,求的值;
(3)是否存在p∈R,使得存在数列,对任意满足?若存在,求出所有这样的p;若不存在,说明理由.
参考答案
一、选择题
1.B
2.D
3.A
4.A
5.A
6.B
7.D
8.B
9.C
10.C
二、填空题
11.-4
12.
(1).
5
(2).
13.
(1).
0
(2).
3
14.
(满足即可)
15.
①②④
三、解答题
16.
(1);
(2)答案不唯一
由余弦定理可得边上的中线的长度为:
;
则由余弦定理可得边上的中线的长度为:
.
17.
(1)证明见解析;(2).
18.
(1)①次;②分布列见解析;期望为
(2)若时,;
若时,;
若时,.
19.
(1);(2)函数的增区间为、,单调递减区间为,最大值为,最小值为.
20.(1);(2).
21.(1)不可以是数列;理由见解析;(2);(3)存在;.
北京卷·数学
第一部分(选择题共40分)
一、选择题共10小题,每小题4分,共40分,在每小题列出的四个选项中,选出符合题目要求的一项.
1.
已知集合,,则(
)
A.
B.
C.
D.
2.
在复平面内,复数满足,则(
)
A.
1
B.i
C.
D.
3.设函数的定义域为,则“函数在上单调递增”是“函数在上的最大值为”的(
)
A.
充分不必要条件
B.
必要不充分条件
C.
充分必要条件
D.
既不充分也不必要条件
4.
某四面体的三视图如图所示,该四面体的表面积为(
)
A.
B.
C.
D.
5.
双曲线过点,离心率为,则该双曲线的标准方程为(
)
A.
B.
C.
D.
6.已知和是两个等差数列,且是常值,若,,,则的值为(
)
A.
B.
100
C.
128
D.
132
7.已知函数,则该函数(
)
A.
奇函数,最大值为2
B.
偶函数,最大值为2
C.
奇函数,最大值为
D.
偶函数,最大值为
8.对24小时内降水在平地上的积水厚度(mm)进行如下定义:
小明用一个圆锥形容器接了24小时的雨水,则这一天的雨水属于哪个等级(
)
A.
小雨
B.
中雨
C.
大雨
D.
暴雨
9.
已知圆,直线,则当的值发生变化时,直线被圆C所截的弦长的最小值为1,则的取值为(
)
A.
B.
C.
D.
10.
数列是递增的整数数列,且,,则的最大值为(
)
A.
9
B.
10
C.
11
D.
12
第二部分(非选择题共110分)
二、填空题5小题,每小题5分,共25分.
11.
的展开式中常数项为__________.
12.
已知抛物线,C焦点为,点在上,且,则的横坐标是_______;作轴于,则_______.
13.
,,,则_______;_______.
14.
若点与点关于轴对称,写出一个符合题意的值___.
15.
已知,给出下列四个结论:
①若,则有两个零点;
②,使得有一个零点;
③,使得有三个零点;
④,使得有三个零点.
以上正确结论的序号是_______.
三、解答题共6小题,共85分,解答应写出文字说明,演算步骤或证明过程.
16.
已知在中,,.
(1)求的大小;
(2)在三个条件中选择一个作为已知,使存在且唯一确定,并求出边上的中线的长度.
①;②周长为;③面积为;
17.
已知正方体,点为中点,直线交平面于点.
(1)求证:点为中点;
(2)若点为棱上一点,且二面角的余弦值为,求的值.
18.
为加快新冠肺炎检测效率,某检测机构采取“k合1检测法”,即将k个人的拭子样本合并检测,若为阴性,则可确定所有样本都是阴性的;若为阳性,则还需要对本组的每个人再做检测.现有100人,已知其中2人感染病毒.
(1)①若采用“10合1检测法”,且两名患者在同一组,求总检测次数;
②已知10人分成一组,分10组,两名感染患者在同一组的概率为,定义随机变量X为总检测次数,求检测次数X的分布列和数学期望E(X);
(2)若采用“5合1检测法”,检测次数Y的期望为E(Y),试比较E(X)和E(Y)的大小(直接写出结果).
19.
已知函数.
(1)若,求在处的切线方程;
(2)若函数在处取得极值,求的单调区间,以及最大值和最小值.
20.
已知椭圆过点,以四个顶点围成的四边形面积为.
(1)求椭圆E的标准方程;
(2)过点P(0,-3)的直线l斜率为k,交椭圆E于不同的两点B,C,直线AB,AC交y=-3于点M、N,若|PM|+|PN|≤15,求k的取值范围.
21.
定义数列:对p∈R,满足:①,;②;③,.
(1)对前4项2,-2,0,1的数列,可以是数列吗?说明理由;
(2)若是数列,求的值;
(3)是否存在p∈R,使得存在数列,对任意满足?若存在,求出所有这样的p;若不存在,说明理由.
参考答案
一、选择题
1.B
2.D
3.A
4.A
5.A
6.B
7.D
8.B
9.C
10.C
二、填空题
11.-4
12.
(1).
5
(2).
13.
(1).
0
(2).
3
14.
(满足即可)
15.
①②④
三、解答题
16.
(1);
(2)答案不唯一
由余弦定理可得边上的中线的长度为:
;
则由余弦定理可得边上的中线的长度为:
.
17.
(1)证明见解析;(2).
18.
(1)①次;②分布列见解析;期望为
(2)若时,;
若时,;
若时,.
19.
(1);(2)函数的增区间为、,单调递减区间为,最大值为,最小值为.
20.(1);(2).
21.(1)不可以是数列;理由见解析;(2);(3)存在;.
同课章节目录
