2022届高考数学一轮复习-立体几何外接球专题教案(Word含解析)
文档属性
| 名称 | 2022届高考数学一轮复习-立体几何外接球专题教案(Word含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-01 12:26:24 | ||
图片预览


文档简介
学
科
数学
教师姓名
教材版本
人教版新教材
学生姓名
所在年级
上课时间
课题名称
外接球问题
教学目标
圆柱和圆锥的外接球模型
2、有公共斜边的两个直角三角形组成的三棱锥外接球
3、利用模型解决相关棱柱和棱锥外接球问题
教学重点
教学难点
知识梳理
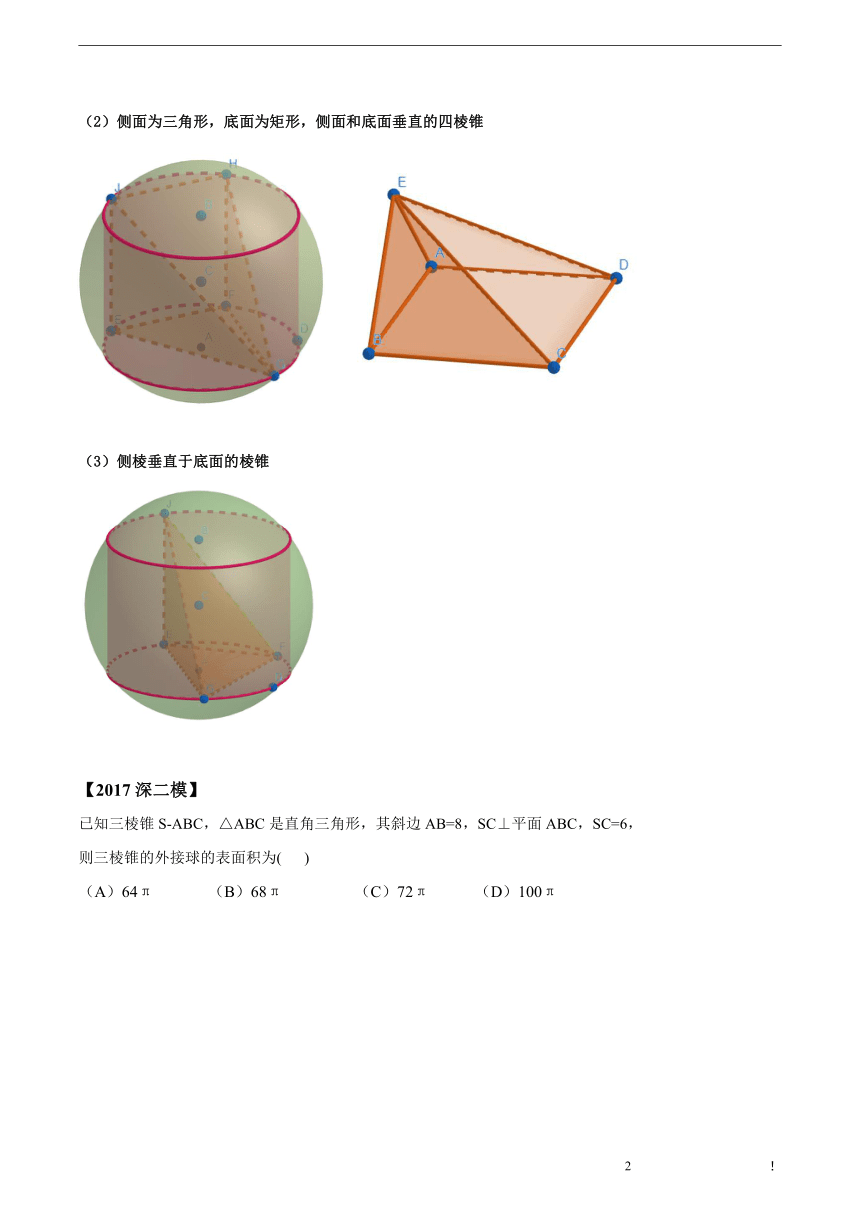
模型一、圆柱外接球
结论:
(R:外接球半径
h:圆柱高
r:圆柱底面半径)
推导:
模型一推广:
(1)直棱柱
(h:圆柱的高
r:直棱柱底面外接圆半径
)
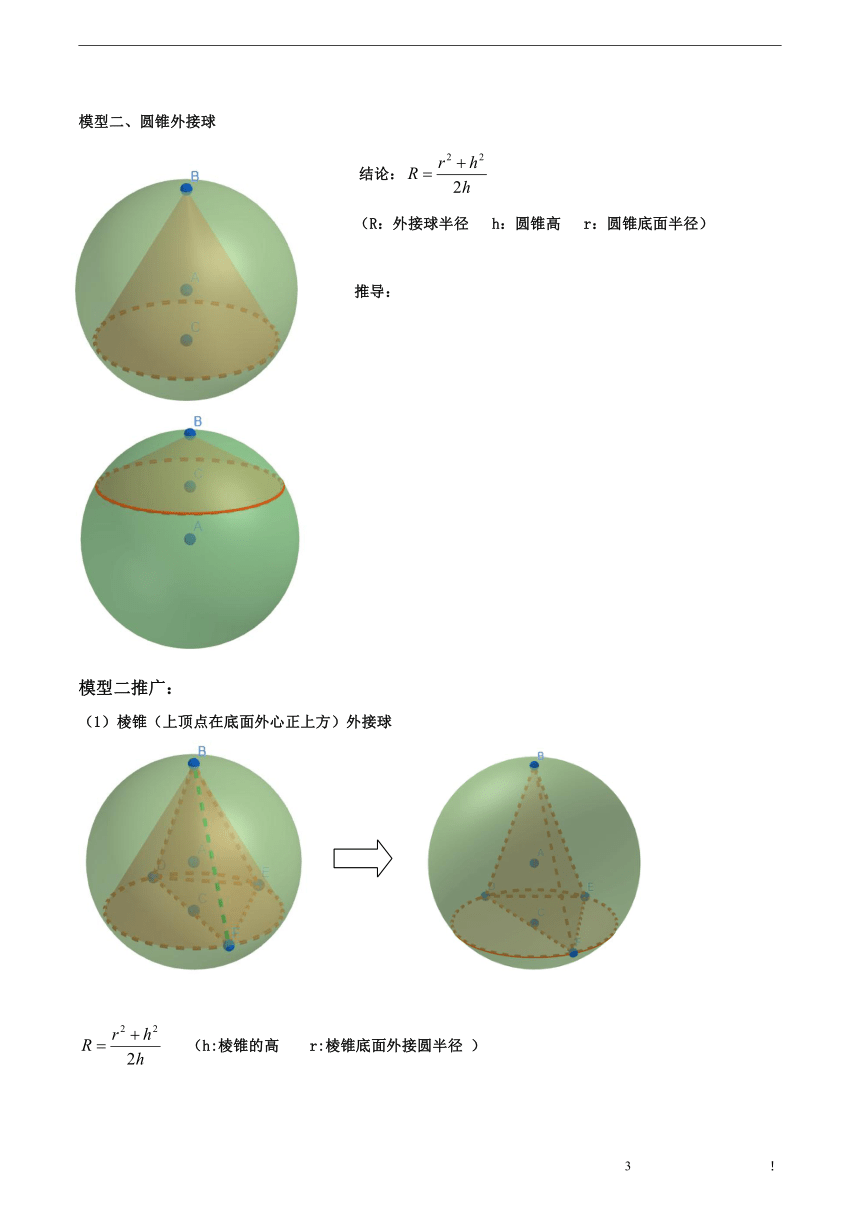
(2)侧面为三角形,底面为矩形,侧面和底面垂直的四棱锥
(3)侧棱垂直于底面的棱锥
【2017深二模】
已知三棱锥S-ABC,△ABC是直角三角形,其斜边AB=8,SC⊥平面ABC,SC=6,
则三棱锥的外接球的表面积为(
)
(A)64π
(B)68π
(C)72π
(D)100π
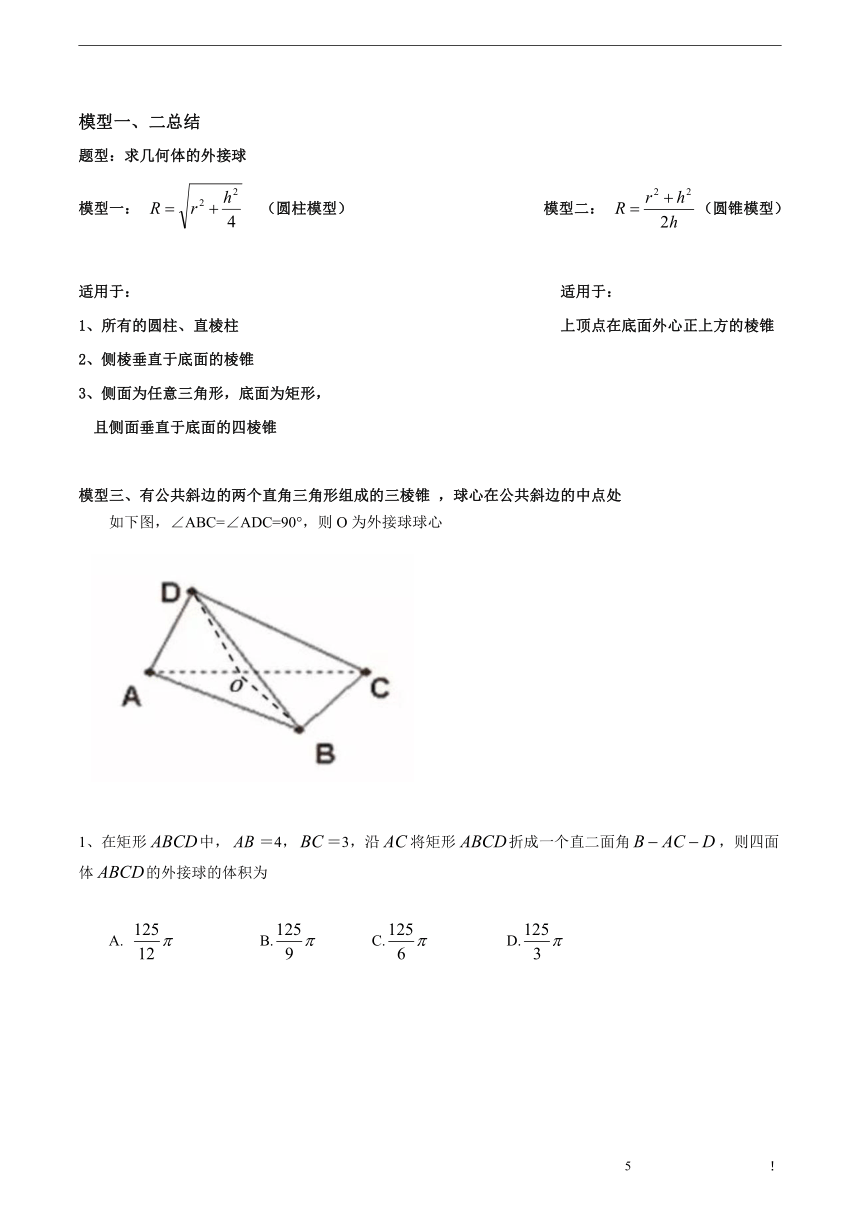
模型二、圆锥外接球
结论:
(R:外接球半径
h:圆锥高
r:圆锥底面半径)
推导:
模型二推广:
(1)棱锥(上顶点在底面外心正上方)外接球
(h:棱锥的高
r:棱锥底面外接圆半径
)
【2018深一模】
如图,网格纸上小正方形的边长为1,某几何体的三视图如图所示,则该几何体的外接球表面积为( )
A.
B.
C.16π
D.25π
【2017全国一卷
文
16】
已知三棱锥S?ABC的所有顶点都在球O的球面上,SC是球O的直径.若平面SCA⊥平面SCB,SA=AC,SB=BC,
三棱锥S?ABC的体积为9,则球O的表面积为______________.
【2019
全国一卷
理
12】
已知三棱锥P?ABC的四个顶点在球O的球面上,PA=PB=PC,△ABC是边长为2的正三角形,E,F分别是PA,AB的中点,∠CEF=90°,则球O的体积为
A.
B.
C.
D.
模型一、二总结
题型:求几何体的外接球
模型一:
(圆柱模型)
模型二:
(圆锥模型)
适用于:
适用于:
1、所有的圆柱、直棱柱
上顶点在底面外心正上方的棱锥
2、侧棱垂直于底面的棱锥
3、侧面为任意三角形,底面为矩形,
且侧面垂直于底面的四棱锥
模型三、有公共斜边的两个直角三角形组成的三棱锥
,球心在公共斜边的中点处
如下图,∠ABC=∠ADC=90°,则O为外接球球心
1、在矩形中,=4,=3,沿将矩形折成一个直二面角,则四面体的外接球的体积为
A.
B.
C.
D.
2.三棱锥的所有顶点都在球的球面上,且,,则该球的体积为
A
B
C
D
专题练习
类型一
构造法(补形法)
【例1】已知是球上的点,
,
,
,则球的表面积等于________________.
【例2】【辽宁省鞍山一中2019届高三三模】刘徽《九章算术?商功》中将底面为长方形,两个三角面与底面垂直的四棱锥体叫做阳马.如图,是一个阳马的三视图,则其外接球的体积为( )
A.
B.
C.
D.
【举一反三】
1、【山东省济宁市2019届高三一模】已知直三棱柱的底面为直角三角形,且两直角边长分别为1和,此三棱柱的高为,则该三棱柱的外接球的体积为
A.
B.
C.
D.
2、【辽宁省师范大学附属中学2019届高三上学期期中】在三棱锥中,,则三棱锥外接球的表面积为( )
A.Π
B.
C.Π
D.
3、【河南省天一大联考2019届高三阶段性测试(五)】某多面体的三视图如图所示,其中正视图是一个直角边为2的等腰直角三角形,侧视图是两直角边分别为2和1的直角三角形,俯视图为一矩形,则该多面体的外接球的表面积为(
)
A.
B.
C.
D.
类型二
正棱锥与球的外接
【例3】正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积为
(
)
A.
B.
C.
D.
【举一反三】
1、球O的球面上有四点S,A,B,C,其中O,A,B,C四点共面,△ABC是边长为2的正三角形,平面SAB⊥平面ABC,则棱锥S?ABC的体积的最大值为( )
A.
B.
C.2
D.4
2.
【四川省德阳市2018届高三二诊】正四面体ABCD的体积为,则正四面体ABCD的外接球的体积为______.
3、【安徽省蚌埠市2019届高三下学期第二次检查】正三棱锥中,,点在棱上,且.正三棱锥的外接球为球,过点作球的截面,截球所得截面面积的最小值为__________.
类型三
直棱柱的外接球
【例4】直三棱柱的各顶点都在同一球面上,若,,
则此球的表面积等于
.
【举一反三】
1、【云南省2019年高三第二次统一检测】已知直三棱柱的顶点都在球的球面上,,,若球的表面积为,则这个直三棱柱的体积是(
)
A.16
B.15
C.
D.
2、已知三棱柱的6个顶点都在球的球面上,,,,则球的半径为( )
A.
B.
C.
D.
3、
正四棱柱的各顶点都在半径为的球面上,则正四棱柱的侧面积有最
值,为
.
答案与解析
类型一
构造法(补形法)
【例1】已知是球上的点,
,
,
,则球的表面积等于________________.
【答案】
【解析】
由已知S,A,B,C是球O表面上的点,所以
,又,
,所以四面体的外接球半径等于以长宽高分别以SA,AB,BC三边长为长方体的外接球的半径,因为,
,所以,所以球的表面积.
【指点迷津】当一三棱锥的三侧棱两两垂直时,可将三棱锥补成一个长方体,将问题转化为长方体(正方体)来解.长方体的外接球即为该三棱锥的外接球.
【例2】【辽宁省鞍山一中2019届高三三模】刘徽《九章算术?商功》中将底面为长方形,两个三角面与底面垂直的四棱锥体叫做阳马.如图,是一个阳马的三视图,则其外接球的体积为( )
A.
B.
C.
D.
【答案】B
【解析】
由题意可知阳马为四棱锥,且四棱锥的底面为长方体的一个底面,四棱锥的高为长方体的一棱长,且阳马的外接球也是长方体的外接球,
由三视图可知四棱锥的底面是边长为1的正方形,四棱锥的高为1,
∴长方体的一个顶点处的三条棱长分别为1,1,1,
∴长方体的对角线为,∴外接球的半径为,
∴外接球的体积为.
故选:B.
【指点迷津】当一四面体或三棱锥的棱长相等时,可以构造正方体,在正方体中构造三棱锥或四面体,利用三棱锥或四面体与正方体的外接球相同来解即可.
【举一反三】
1、【山东省济宁市2019届高三一模】已知直三棱柱的底面为直角三角形,且两直角边长分别为1和,此三棱柱的高为,则该三棱柱的外接球的体积为
A.
B.
C.
D.
【答案】C
【解析】
如图所示,将直三棱柱补充为长方体,
则该长方体的体对角线为,
设长方体的外接球的半径为,则,,
所以该长方体的外接球的体积,
故选C.
2、【辽宁省师范大学附属中学2019届高三上学期期中】在三棱锥中,,则三棱锥外接球的表面积为( )
A.
B.
C.
D.
【答案】C
【解析】
解:如图,
把三棱锥补形为长方体,设长方体的长、宽、高分别为,
则,
∴三棱锥外接球的半径
∴三棱锥外接球的表面积为.
故选:C.
3、【河南省天一大联考2019届高三阶段性测试(五)】某多面体的三视图如图所示,其中正视图是一个直角边为2的等腰直角三角形,侧视图是两直角边分别为2和1的直角三角形,俯视图为一矩形,则该多面体的外接球的表面积为(
)
A.
B.
C.
D.
【答案】C
【解析】
由三视图可得,该几何体为一个三棱锥,放在长、宽、高分别为2,1,2的长方体中,此三棱锥和长方体的外接球是同一个,长方体的外接球的球心在体对角线的中点处,易得其外接球的直径为,从而外接球的表面积为.
故答案为:C.
类型二
正棱锥与球的外接
【例3】正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积为
(
)
A.
B.
C.
D.
【答案】A.
【指点迷津】求正棱锥外接球的表面积或体积,应先求其半径,在棱锥的高上取一点作为外接球的球心,构造直角三角形,利用勾股定理求半径.
【举一反三】
1、球O的球面上有四点S,A,B,C,其中O,A,B,C四点共面,△ABC是边长为2的正三角形,平面SAB⊥平面ABC,则棱锥S?ABC的体积的最大值为( )
A.
B.
C.2
D.4
【答案】A
【解析】
(1)由于平面SAB⊥平面ABC,所以点S在平面ABC上的射影H落在AB上,根据球的对称性可知,当S在“最高点”,即H为AB的中点时,SH最大,此时棱锥S?ABC的体积最大.学科
网
因为△ABC是边长为2的正三角形,所以球的半径r=OC=CH=××2=.
在Rt△SHO中,OH=OC=,
所以SH==1,
故所求体积的最大值为××22×1=.
2.
【四川省德阳市2018届高三二诊】正四面体ABCD的体积为,则正四面体ABCD的外接球的体积为______.
【答案】
【解析】
解:如图,
设正四面体ABCD的棱长为,过A作AD⊥BC,
设等边三角形ABC的中心为O,则,
,
,即.
再设正四面体ABCD的外接球球心为G,连接GA,
则,即.
∴正四面体ABCD的外接球的体积为.
故答案为:.
3、【安徽省蚌埠市2019届高三下学期第二次检查】正三棱锥中,,点在棱上,且.正三棱锥的外接球为球,过点作球的截面,截球所得截面面积的最小值为__________.
【答案】
【解析】
因为,所以,
所以,同理,
故可把正三棱锥补成正方体(如图所示),其外接球即为球,直径为正方体的体对角线,故,设的中点为,连接,
则且,所以,
当平面时,平面截球的截面面积最小,
此时截面为圆面,其半径为,故截面的面积为.填.
类型三
直棱柱的外接球
【例4】直三棱柱的各顶点都在同一球面上,若,,
则此球的表面积等于
.
【答案】
【解析】在中,,可得,由正弦定理,可得外接圆半径r=2,设此圆圆心为,球心为,在中,易得球半径,故此球的表面积为.
【指点迷津】直棱柱的外接球的球心在上、下底面的外接圆的圆心的连线上,确定球心,用球心、一底面的外接圆的圆心,一顶点构成一个直角三角形,用勾股定理得关于外接球半径的关系式,可球的半径.
【举一反三】
1、【云南省2019年高三第二次统一检测】已知直三棱柱的顶点都在球的球面上,,,若球的表面积为,则这个直三棱柱的体积是(
)
A.16
B.15
C.
D.
【答案】A
【解析】
由题,
,
因为,,易知三角形ABC为等腰直角三角形,
故三棱柱的高
故体积
故选A
2、已知三棱柱的6个顶点都在球的球面上,若,,,则球的半径为
( )
A.
B.
C.
D.
【答案】C
【解析】由球心作面ABC的垂线,则垂足为BC中点M.计算AM=,由垂径定理,OM=6,所以半径R=,选C.
3、
正四棱柱的各顶点都在半径为的球面上,则正四棱柱的侧面积有最
值,为
.
【答案】大
1
!
科
数学
教师姓名
教材版本
人教版新教材
学生姓名
所在年级
上课时间
课题名称
外接球问题
教学目标
圆柱和圆锥的外接球模型
2、有公共斜边的两个直角三角形组成的三棱锥外接球
3、利用模型解决相关棱柱和棱锥外接球问题
教学重点
教学难点
知识梳理
模型一、圆柱外接球
结论:
(R:外接球半径
h:圆柱高
r:圆柱底面半径)
推导:
模型一推广:
(1)直棱柱
(h:圆柱的高
r:直棱柱底面外接圆半径
)
(2)侧面为三角形,底面为矩形,侧面和底面垂直的四棱锥
(3)侧棱垂直于底面的棱锥
【2017深二模】
已知三棱锥S-ABC,△ABC是直角三角形,其斜边AB=8,SC⊥平面ABC,SC=6,
则三棱锥的外接球的表面积为(
)
(A)64π
(B)68π
(C)72π
(D)100π
模型二、圆锥外接球
结论:
(R:外接球半径
h:圆锥高
r:圆锥底面半径)
推导:
模型二推广:
(1)棱锥(上顶点在底面外心正上方)外接球
(h:棱锥的高
r:棱锥底面外接圆半径
)
【2018深一模】
如图,网格纸上小正方形的边长为1,某几何体的三视图如图所示,则该几何体的外接球表面积为( )
A.
B.
C.16π
D.25π
【2017全国一卷
文
16】
已知三棱锥S?ABC的所有顶点都在球O的球面上,SC是球O的直径.若平面SCA⊥平面SCB,SA=AC,SB=BC,
三棱锥S?ABC的体积为9,则球O的表面积为______________.
【2019
全国一卷
理
12】
已知三棱锥P?ABC的四个顶点在球O的球面上,PA=PB=PC,△ABC是边长为2的正三角形,E,F分别是PA,AB的中点,∠CEF=90°,则球O的体积为
A.
B.
C.
D.
模型一、二总结
题型:求几何体的外接球
模型一:
(圆柱模型)
模型二:
(圆锥模型)
适用于:
适用于:
1、所有的圆柱、直棱柱
上顶点在底面外心正上方的棱锥
2、侧棱垂直于底面的棱锥
3、侧面为任意三角形,底面为矩形,
且侧面垂直于底面的四棱锥
模型三、有公共斜边的两个直角三角形组成的三棱锥
,球心在公共斜边的中点处
如下图,∠ABC=∠ADC=90°,则O为外接球球心
1、在矩形中,=4,=3,沿将矩形折成一个直二面角,则四面体的外接球的体积为
A.
B.
C.
D.
2.三棱锥的所有顶点都在球的球面上,且,,则该球的体积为
A
B
C
D
专题练习
类型一
构造法(补形法)
【例1】已知是球上的点,
,
,
,则球的表面积等于________________.
【例2】【辽宁省鞍山一中2019届高三三模】刘徽《九章算术?商功》中将底面为长方形,两个三角面与底面垂直的四棱锥体叫做阳马.如图,是一个阳马的三视图,则其外接球的体积为( )
A.
B.
C.
D.
【举一反三】
1、【山东省济宁市2019届高三一模】已知直三棱柱的底面为直角三角形,且两直角边长分别为1和,此三棱柱的高为,则该三棱柱的外接球的体积为
A.
B.
C.
D.
2、【辽宁省师范大学附属中学2019届高三上学期期中】在三棱锥中,,则三棱锥外接球的表面积为( )
A.Π
B.
C.Π
D.
3、【河南省天一大联考2019届高三阶段性测试(五)】某多面体的三视图如图所示,其中正视图是一个直角边为2的等腰直角三角形,侧视图是两直角边分别为2和1的直角三角形,俯视图为一矩形,则该多面体的外接球的表面积为(
)
A.
B.
C.
D.
类型二
正棱锥与球的外接
【例3】正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积为
(
)
A.
B.
C.
D.
【举一反三】
1、球O的球面上有四点S,A,B,C,其中O,A,B,C四点共面,△ABC是边长为2的正三角形,平面SAB⊥平面ABC,则棱锥S?ABC的体积的最大值为( )
A.
B.
C.2
D.4
2.
【四川省德阳市2018届高三二诊】正四面体ABCD的体积为,则正四面体ABCD的外接球的体积为______.
3、【安徽省蚌埠市2019届高三下学期第二次检查】正三棱锥中,,点在棱上,且.正三棱锥的外接球为球,过点作球的截面,截球所得截面面积的最小值为__________.
类型三
直棱柱的外接球
【例4】直三棱柱的各顶点都在同一球面上,若,,
则此球的表面积等于
.
【举一反三】
1、【云南省2019年高三第二次统一检测】已知直三棱柱的顶点都在球的球面上,,,若球的表面积为,则这个直三棱柱的体积是(
)
A.16
B.15
C.
D.
2、已知三棱柱的6个顶点都在球的球面上,,,,则球的半径为( )
A.
B.
C.
D.
3、
正四棱柱的各顶点都在半径为的球面上,则正四棱柱的侧面积有最
值,为
.
答案与解析
类型一
构造法(补形法)
【例1】已知是球上的点,
,
,
,则球的表面积等于________________.
【答案】
【解析】
由已知S,A,B,C是球O表面上的点,所以
,又,
,所以四面体的外接球半径等于以长宽高分别以SA,AB,BC三边长为长方体的外接球的半径,因为,
,所以,所以球的表面积.
【指点迷津】当一三棱锥的三侧棱两两垂直时,可将三棱锥补成一个长方体,将问题转化为长方体(正方体)来解.长方体的外接球即为该三棱锥的外接球.
【例2】【辽宁省鞍山一中2019届高三三模】刘徽《九章算术?商功》中将底面为长方形,两个三角面与底面垂直的四棱锥体叫做阳马.如图,是一个阳马的三视图,则其外接球的体积为( )
A.
B.
C.
D.
【答案】B
【解析】
由题意可知阳马为四棱锥,且四棱锥的底面为长方体的一个底面,四棱锥的高为长方体的一棱长,且阳马的外接球也是长方体的外接球,
由三视图可知四棱锥的底面是边长为1的正方形,四棱锥的高为1,
∴长方体的一个顶点处的三条棱长分别为1,1,1,
∴长方体的对角线为,∴外接球的半径为,
∴外接球的体积为.
故选:B.
【指点迷津】当一四面体或三棱锥的棱长相等时,可以构造正方体,在正方体中构造三棱锥或四面体,利用三棱锥或四面体与正方体的外接球相同来解即可.
【举一反三】
1、【山东省济宁市2019届高三一模】已知直三棱柱的底面为直角三角形,且两直角边长分别为1和,此三棱柱的高为,则该三棱柱的外接球的体积为
A.
B.
C.
D.
【答案】C
【解析】
如图所示,将直三棱柱补充为长方体,
则该长方体的体对角线为,
设长方体的外接球的半径为,则,,
所以该长方体的外接球的体积,
故选C.
2、【辽宁省师范大学附属中学2019届高三上学期期中】在三棱锥中,,则三棱锥外接球的表面积为( )
A.
B.
C.
D.
【答案】C
【解析】
解:如图,
把三棱锥补形为长方体,设长方体的长、宽、高分别为,
则,
∴三棱锥外接球的半径
∴三棱锥外接球的表面积为.
故选:C.
3、【河南省天一大联考2019届高三阶段性测试(五)】某多面体的三视图如图所示,其中正视图是一个直角边为2的等腰直角三角形,侧视图是两直角边分别为2和1的直角三角形,俯视图为一矩形,则该多面体的外接球的表面积为(
)
A.
B.
C.
D.
【答案】C
【解析】
由三视图可得,该几何体为一个三棱锥,放在长、宽、高分别为2,1,2的长方体中,此三棱锥和长方体的外接球是同一个,长方体的外接球的球心在体对角线的中点处,易得其外接球的直径为,从而外接球的表面积为.
故答案为:C.
类型二
正棱锥与球的外接
【例3】正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积为
(
)
A.
B.
C.
D.
【答案】A.
【指点迷津】求正棱锥外接球的表面积或体积,应先求其半径,在棱锥的高上取一点作为外接球的球心,构造直角三角形,利用勾股定理求半径.
【举一反三】
1、球O的球面上有四点S,A,B,C,其中O,A,B,C四点共面,△ABC是边长为2的正三角形,平面SAB⊥平面ABC,则棱锥S?ABC的体积的最大值为( )
A.
B.
C.2
D.4
【答案】A
【解析】
(1)由于平面SAB⊥平面ABC,所以点S在平面ABC上的射影H落在AB上,根据球的对称性可知,当S在“最高点”,即H为AB的中点时,SH最大,此时棱锥S?ABC的体积最大.学科
网
因为△ABC是边长为2的正三角形,所以球的半径r=OC=CH=××2=.
在Rt△SHO中,OH=OC=,
所以SH==1,
故所求体积的最大值为××22×1=.
2.
【四川省德阳市2018届高三二诊】正四面体ABCD的体积为,则正四面体ABCD的外接球的体积为______.
【答案】
【解析】
解:如图,
设正四面体ABCD的棱长为,过A作AD⊥BC,
设等边三角形ABC的中心为O,则,
,
,即.
再设正四面体ABCD的外接球球心为G,连接GA,
则,即.
∴正四面体ABCD的外接球的体积为.
故答案为:.
3、【安徽省蚌埠市2019届高三下学期第二次检查】正三棱锥中,,点在棱上,且.正三棱锥的外接球为球,过点作球的截面,截球所得截面面积的最小值为__________.
【答案】
【解析】
因为,所以,
所以,同理,
故可把正三棱锥补成正方体(如图所示),其外接球即为球,直径为正方体的体对角线,故,设的中点为,连接,
则且,所以,
当平面时,平面截球的截面面积最小,
此时截面为圆面,其半径为,故截面的面积为.填.
类型三
直棱柱的外接球
【例4】直三棱柱的各顶点都在同一球面上,若,,
则此球的表面积等于
.
【答案】
【解析】在中,,可得,由正弦定理,可得外接圆半径r=2,设此圆圆心为,球心为,在中,易得球半径,故此球的表面积为.
【指点迷津】直棱柱的外接球的球心在上、下底面的外接圆的圆心的连线上,确定球心,用球心、一底面的外接圆的圆心,一顶点构成一个直角三角形,用勾股定理得关于外接球半径的关系式,可球的半径.
【举一反三】
1、【云南省2019年高三第二次统一检测】已知直三棱柱的顶点都在球的球面上,,,若球的表面积为,则这个直三棱柱的体积是(
)
A.16
B.15
C.
D.
【答案】A
【解析】
由题,
,
因为,,易知三角形ABC为等腰直角三角形,
故三棱柱的高
故体积
故选A
2、已知三棱柱的6个顶点都在球的球面上,若,,,则球的半径为
( )
A.
B.
C.
D.
【答案】C
【解析】由球心作面ABC的垂线,则垂足为BC中点M.计算AM=,由垂径定理,OM=6,所以半径R=,选C.
3、
正四棱柱的各顶点都在半径为的球面上,则正四棱柱的侧面积有最
值,为
.
【答案】大
1
!
同课章节目录
