2022届高考数学一轮复习-解三角形专题教案(一)Word版
文档属性
| 名称 | 2022届高考数学一轮复习-解三角形专题教案(一)Word版 |  | |
| 格式 | doc | ||
| 文件大小 | 237.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-01 22:06:02 | ||
图片预览



文档简介
学 科 数学 教师姓名
上课时间
学生姓名
所在年级
教材版本 人教版
课程名称 解三角形
教学目标 1、三角形解的个数
2、中线长、角平分线长
教学重点
教学难点
典例分析
类型一:求边或求角
类型二:边角互化—化简
例1:(2017?新课标Ⅱ)△ABC的内角A,B,C的对边分别为a,b,c,若2bcosB=acosC+ccosA,则B=________.
例2:(2011·全国)△ABC的内角A、B、C的对边分别为a、b、c,asin A+csin C-asin C=bsin B. 求B
例3:(2016浙江)在△ABC中,内角A,B,C所对的边分别为a,b,c. 已知b+c=2acosB. 证明:A=2B;
例4:(2018?卷Ⅰ)△ABC的内角A,B,C的对边分别为a,b,c.已知 bsinC+ csinB=4asinBsinC , b2+c2-a2=8,
则△ABC的面积为________.
类型三:判断三角形形状
例1、在中,已知分别为角A,B,C的对边,
(1)试确定形状。
(2)若,试确定形状。
例2、在中,已知,试判断三角形的形状。
例3、已知在中,,且,试判断三角形的形状。
例4、(2016上海)已知的三边长分别为3,5,7,则该三角形的外接圆半径等于______
例5、在△ABC中,若a=9 , b=10 , c=12 , 则△ABC的形状是_________。
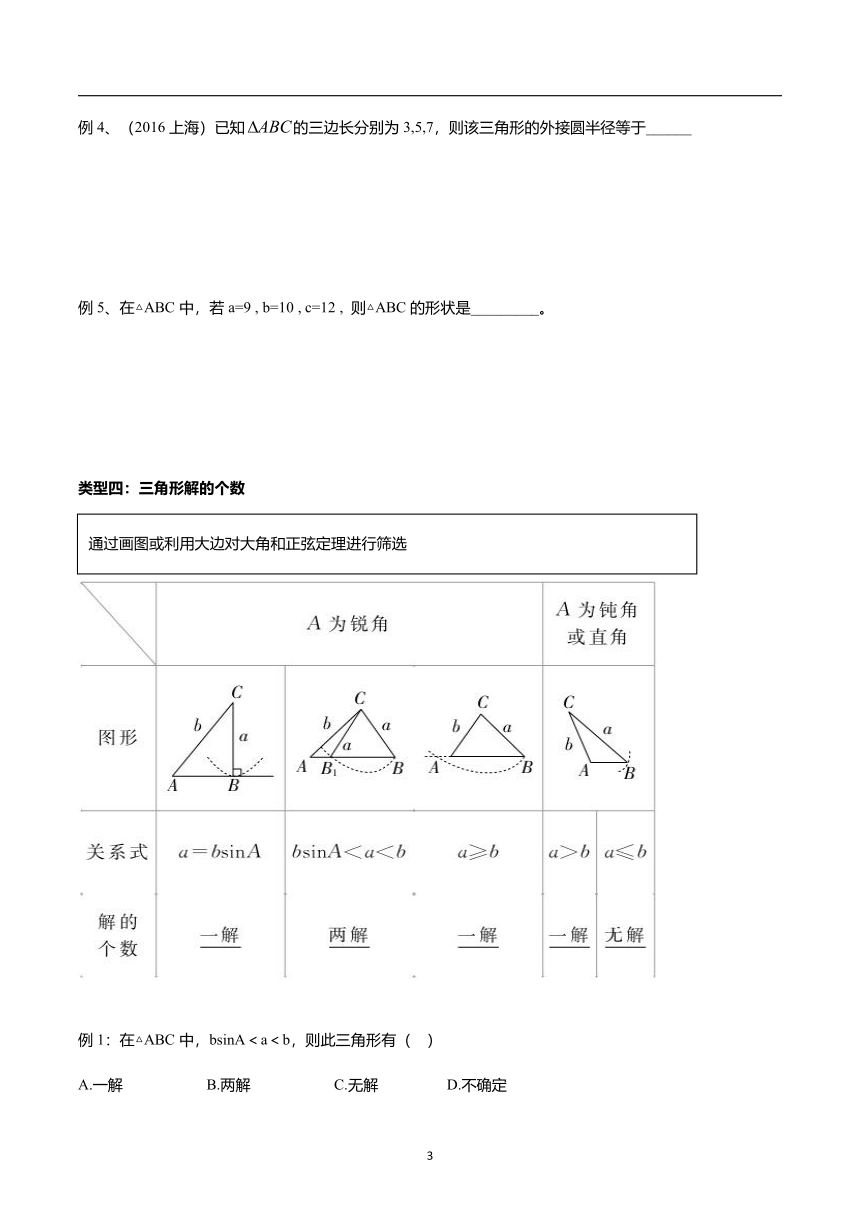
类型四:三角形解的个数
例1:在△ABC中,bsinA<a<b,则此三角形有( )
A.一解 ?B.两解?? C.无解? D.不确定
【能解出特殊角度】
例2:已知△ABC中,,,B=45°,试判断符合条件的△ABC有多少个?
【解不出特殊角度】
例3:已知△ABC中,,,C=60°,试判断符合条件的△ABC有多少个?
例4: 已知△ABC中,,,A=45°,试判断符合条件的△ABC有多少个?
例5:在中,分别根据下列条件解三角形,其中有两解的是( )
A、,,; B、,,;
C、,,; D、,,。
例6:在中,
【已知解的个数求范围】
例7:已知△ABC中,满足b=2 , B=60?的三角形有两解,则边长a的取值范围是( )
例8:如果满足∠ABC=60?, AC=12 , BC=k的锐角三角形ABC有且只有一个,那么实数k的取值范围是()
类型五:求边、角、面积范围或最值
例1:已知△ABC的三内角A,B,C所对的边分别是a,b,c,向量m=(cos B,cos C),n=(2a+c,b),且m⊥n
(1)求角B的大小;
(2)若b=,求a+c的范围.
例2:在△ABC中,a, b, c分别为内角A, B, C的对边,且
(Ⅰ)求A的大小;
(Ⅱ)求的最大值.
例3:在△ABC中,,.
(1)若b+c=6 ,且b(2)求△ABC的面积的最大值.
例4:在△ABC中,已知(sinA+sinB)(a-b)=c·(sinC+sinB).
(1)求角A;
(2)若,求△ABC周长的取值范围。
类型六:中线
例1:在△ABC中,AB=2 , AC=3 , BC边上的中线AD=2, 求△ABC的面积S
例2:在△ABC中,,
求a : b : c
若BD为AC边的中线,且, 求△ABC的面积
类型七:角平分线
例1:【2015全国Ⅱ卷 理17】
中,是上的点,平分,面积是面积的2倍.
(Ⅰ) 求;
(Ⅱ)若,,求和的长.
例2:已知AD为△ABC中角A的平分线,AB=3, AC=5, ∠BAC=120°, 则AD的长为
1
上课时间
学生姓名
所在年级
教材版本 人教版
课程名称 解三角形
教学目标 1、三角形解的个数
2、中线长、角平分线长
教学重点
教学难点
典例分析
类型一:求边或求角
类型二:边角互化—化简
例1:(2017?新课标Ⅱ)△ABC的内角A,B,C的对边分别为a,b,c,若2bcosB=acosC+ccosA,则B=________.
例2:(2011·全国)△ABC的内角A、B、C的对边分别为a、b、c,asin A+csin C-asin C=bsin B. 求B
例3:(2016浙江)在△ABC中,内角A,B,C所对的边分别为a,b,c. 已知b+c=2acosB. 证明:A=2B;
例4:(2018?卷Ⅰ)△ABC的内角A,B,C的对边分别为a,b,c.已知 bsinC+ csinB=4asinBsinC , b2+c2-a2=8,
则△ABC的面积为________.
类型三:判断三角形形状
例1、在中,已知分别为角A,B,C的对边,
(1)试确定形状。
(2)若,试确定形状。
例2、在中,已知,试判断三角形的形状。
例3、已知在中,,且,试判断三角形的形状。
例4、(2016上海)已知的三边长分别为3,5,7,则该三角形的外接圆半径等于______
例5、在△ABC中,若a=9 , b=10 , c=12 , 则△ABC的形状是_________。
类型四:三角形解的个数
例1:在△ABC中,bsinA<a<b,则此三角形有( )
A.一解 ?B.两解?? C.无解? D.不确定
【能解出特殊角度】
例2:已知△ABC中,,,B=45°,试判断符合条件的△ABC有多少个?
【解不出特殊角度】
例3:已知△ABC中,,,C=60°,试判断符合条件的△ABC有多少个?
例4: 已知△ABC中,,,A=45°,试判断符合条件的△ABC有多少个?
例5:在中,分别根据下列条件解三角形,其中有两解的是( )
A、,,; B、,,;
C、,,; D、,,。
例6:在中,
【已知解的个数求范围】
例7:已知△ABC中,满足b=2 , B=60?的三角形有两解,则边长a的取值范围是( )
例8:如果满足∠ABC=60?, AC=12 , BC=k的锐角三角形ABC有且只有一个,那么实数k的取值范围是()
类型五:求边、角、面积范围或最值
例1:已知△ABC的三内角A,B,C所对的边分别是a,b,c,向量m=(cos B,cos C),n=(2a+c,b),且m⊥n
(1)求角B的大小;
(2)若b=,求a+c的范围.
例2:在△ABC中,a, b, c分别为内角A, B, C的对边,且
(Ⅰ)求A的大小;
(Ⅱ)求的最大值.
例3:在△ABC中,,.
(1)若b+c=6 ,且b
例4:在△ABC中,已知(sinA+sinB)(a-b)=c·(sinC+sinB).
(1)求角A;
(2)若,求△ABC周长的取值范围。
类型六:中线
例1:在△ABC中,AB=2 , AC=3 , BC边上的中线AD=2, 求△ABC的面积S
例2:在△ABC中,,
求a : b : c
若BD为AC边的中线,且, 求△ABC的面积
类型七:角平分线
例1:【2015全国Ⅱ卷 理17】
中,是上的点,平分,面积是面积的2倍.
(Ⅰ) 求;
(Ⅱ)若,,求和的长.
例2:已知AD为△ABC中角A的平分线,AB=3, AC=5, ∠BAC=120°, 则AD的长为
1
同课章节目录
