2022届高考数学一轮复习- 空间直线、平面垂直的判定与性质教案Word版
文档属性
| 名称 | 2022届高考数学一轮复习- 空间直线、平面垂直的判定与性质教案Word版 |  | |
| 格式 | doc | ||
| 文件大小 | 5.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-01 22:07:12 | ||
图片预览



文档简介
教 师
学生姓名
教材版本
学 科 数学 年级
上课时间
课 题 平行垂直
教学目 标 平行垂直
教 学 重 点 平行垂直
教 学 过 程
一、知识梳理
1.直线和平面垂直:
(1)定义:如果一条直线和一个平面内的任意一条直线都垂直,那么就说直线和平面互相垂直.记作:
(2)判定定理:如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面.
即
(3)性质定理:如果两条直线同垂直于一个平面,那么这两条直线平行.即
2. 三垂线定理:
(1)斜线在平面内的射影:从斜线上斜足以外的一点向平面引垂线,过斜足和垂足的直线叫做斜线在这个平面内的射影.注:垂线段比任何一条斜线段短.
⑵三垂线定理:在平面内的一条直线,如果它和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直. 即
三垂线定理的逆定理:在平面内的一条直线,如果它和这个平面的一条斜线垂直,那么它也和这条斜线的射影垂直.即
二、专题精讲
题型一 线线、线面、面面垂直关系的综合问题
例题1:为两条不重合的直线,为三个互不重合的平面,给出下面四个命题:
①;②;
;
其中正确的命题有( )
A 1个 B 2个 C 3个 D 4个
【反思小结】与平行问题一样,本题主要考查线线、线面、面面的垂直问题,高考几乎年年都单独考查学生对线面、面面垂直的判定定理和性质定理的准确、深刻的理解,考查学生对符号语言、图形语言、文字语言熟练转换的能力,以选择题、填空题居多,既可能就平行或垂直单独进行考查,又可能在平行中渗透垂直,垂直中兼顾平行,既考查空间想象能力,又考查逻辑推理能力。
拓展练习:设是两条不同的直线,是两个不同的平面,下列命题中正确的是( )
A. B.
C. D.
题型二 线面垂直的定义、判定定理和性质定理及其应用
1.如图,四棱锥P-ABCD中,平面ABCD,,
求证:;
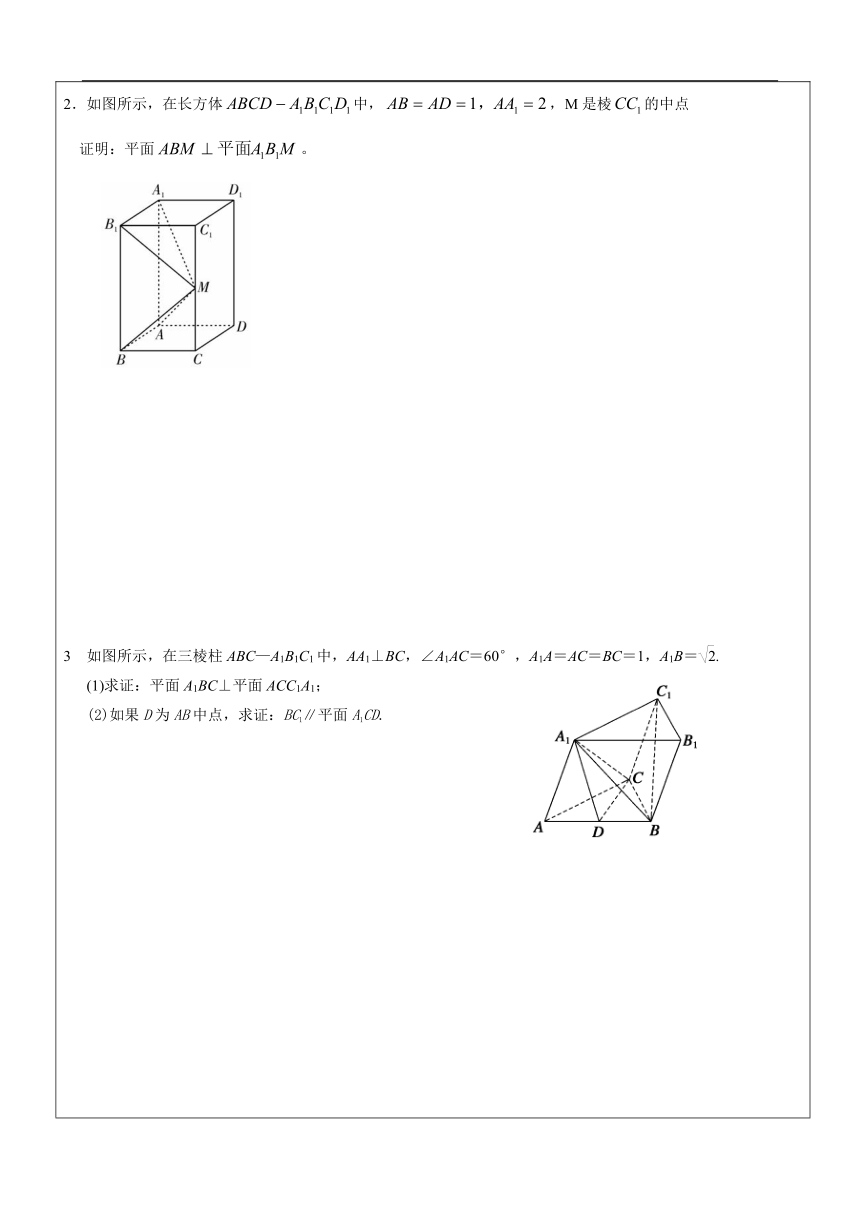
2.如图所示,在长方体中,,M是棱的中点
证明:平面。
3 如图所示,在三棱柱ABC—A1B1C1中,AA1⊥BC,∠A1AC=60°,A1A=AC=BC=1,A1B=.
(1)求证:平面A1BC⊥平面ACC1A1;
(2)如果D为AB中点,求证:BC1∥平面A1CD.
三、学法提炼
证明线线、线面、面面平行或垂直时需要注意以下几点:(1)由已知想性质,由求证想判定,即分析法和综合法相结合寻找解题思路.(2)利用题设条件添加适当的辅助线或辅助面是解题的常用方法之一,例如:证明平行时遇到中点要设法构造中位线或平行四边形,而证明垂直时则要构造等腰三角形的中线、高线、角平分线三线合一;证明线面、面面垂直时要注意条件的充分性,已知线面垂直或面面垂直时要用好性质,构造适当的辅助面.
1.新教材中删去了三垂线定理,用传统方法求角和距离的要求也相当低,教学中不宜过分强调,但是必须明确斜线、垂线、以及斜线在平面内的射影之间的联系,会作出斜线在平面内的射影,从而为线线或线面垂直做好铺垫.
2.线面垂直的性质可以用来证明两条直线垂直和平行,也可以实现面面垂直的证明,因此线面垂直关系是线线垂直、线线平行、面面垂直的枢纽,进而是整个线面位置关系的核心.
3.在线面垂直的定义中,一定要弄清楚不可缺少.
4.面面垂直的性质的理解中三个条仵也不可缺少,即:①两个平面垂直;②其中一个平面内的直线;⑧垂直于交线,所以无论何时见到已知两个平面垂直,都要首先找其交线,看是否存在直线垂直于交线来决定是否该作辅助线,这样就能目标明确,事半功倍.
5.注意充分利用好身边的物体进行比划和举反例,如将课室当成六面体,将书桌、课本、纸张当成平面,笔当成直线等,这些方法依然是解决空间线面位置关系的最佳方法。
1:如图,在四棱锥:中,底面ABCD,,
,E是PC的中点,
证明:(1);(2)平面ABE。
【反思小结】本题考查直线与直线垂直、直线与平面垂直等基础知识,考查空间想象能力和推理论证能力,立体几何的证明关键是学会分析和掌握一些常规的证明方法,如:已知中点证明垂直时要首先考虑等腰三角形中的“三线合一”已知线段或角度等数量关系较多时最好标示出来,充分进行计算,从而发现蕴含的垂直等关系;已知线面垂直时会有哪些结论,是选择线线垂直还是选择面面垂直;要证明结论或要得到哪个结论,就必须满足什么条件等。
2:在四棱锥中,侧棱SA= SC,底面ABCD是菱形,AC与BD交于O点.
(1)求证:平面SBD;
(2)若E为BC的中点,点P在侧面内及其边界上运动,并保持,试指出动点P的转迹,并证明你的结论.
3:如图,AB为圆O的直径,点E、F在圆O上,且,矩形ABCD所在的平面和圆O所在的平面互相垂直,且AB =2,AD =EF=1
(1)求证:平面平面CBF:
(2)设FC的中点为M,求证:平面DAF
(3)设平面CBF将几何体EFABCD分成的两个锥体的体积分别为,求。
学法升华
方法与技巧
1.证明线面垂直的方法
(1)线面垂直的定义:a与α内任何直线都垂直?a⊥α;
(2)判定定理1:?l⊥α;
(3)判定定理2:a∥b,a⊥α?b⊥α;
(4)面面平行的性质:α∥β,a⊥α?a⊥β;
(5)面面垂直的性质:α⊥β,α∩β=l,a?α,a⊥l?a⊥β.
2. 证明线线垂直的方法
(1)定义:两条直线所成的角为90°;
(2)平面几何中证明线线垂直的方法;
(3)线面垂直的性质:a⊥α,b?α?a⊥b;
(4)线面垂直的性质:a⊥α,b∥α?a⊥b.
3. 证明面面垂直的方法
(1)利用定义:两个平面相交,所成的二面角是直二面角;
(2)判定定理:a?α,a⊥β?α⊥β.
失误与防范
1. 垂直关系的转化
在证明两平面垂直时一般先从现有的直线中寻找平面的垂线,若这样的直线图中不存在,则可通过作辅助线来解决.如有平面垂直时,一般要用性质定理,在一个平面内作交线的垂线,使之转化为线面垂直,然后进一步转化为线线垂直.故熟练掌握“线线垂直”、“面面垂直”间的转化条件是解决这类问题的关键.
2.面面垂直的性质定理是作辅助线的一个重要依据.我们要作一个平面的一条垂线,通常是先找这个平面的一个垂面,在这个垂面中,作交线的垂线即可.
课后作业
1.若是互不相同的空间直线,是不重合的两个平面,则下列命题中为真命题的是( )
A.若,则 B.若,则
C.若,则 D.若,则
2.如图,直线PA垂直于以AB为直径的圆所在的平面,C为圆上异于点A和点B的任意一点,有下列四个结论:
①; ; ;
其中不正确的是
3.如图,在正四面体P-ABC中,D、E、F分别是AB、BC、CA的中点,下面四个结论不成立的是 ( )
A.BC∥平面PDF
B.DF⊥平面PAE
C.平面PDF⊥平面PAE
D.平面PDE⊥平面ABC
4.设、β是两个不同的平面,l是一条直线,以下命题正确的是( )
A.若l⊥,⊥β,则l?β B.若l∥,∥β,则l?β
C.若l⊥,∥β,则l⊥β D.若l∥,⊥β,则l⊥β
5.如图所示,在四棱锥P-ABCD中,PA⊥底面ABCD,且底面各边都相等,M是PC上的一动点,当点M满足________时,平面MBD⊥平面PCD.(只要填写一个你认为是正确的条件即可)
6.如图,在直三棱柱ABC-A1B1C1中,AC=3,AB=5, cos∠BAC=.
(1)求证:BC⊥AC1;
(2)若D是AB的中点,求证:AC1∥平面CDB1.
7.如图,在正方体ABCD-A1B1C1D1中,M、N、G分别是A1A,D1C,AD的中点.求证:
(1)MN∥平面ABCD;
(2)MN⊥平面B1BG.
课后小结 上课情况:
课后需再巩固的内容:
组长签字:____________
学生姓名
教材版本
学 科 数学 年级
上课时间
课 题 平行垂直
教学目 标 平行垂直
教 学 重 点 平行垂直
教 学 过 程
一、知识梳理
1.直线和平面垂直:
(1)定义:如果一条直线和一个平面内的任意一条直线都垂直,那么就说直线和平面互相垂直.记作:
(2)判定定理:如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面.
即
(3)性质定理:如果两条直线同垂直于一个平面,那么这两条直线平行.即
2. 三垂线定理:
(1)斜线在平面内的射影:从斜线上斜足以外的一点向平面引垂线,过斜足和垂足的直线叫做斜线在这个平面内的射影.注:垂线段比任何一条斜线段短.
⑵三垂线定理:在平面内的一条直线,如果它和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直. 即
三垂线定理的逆定理:在平面内的一条直线,如果它和这个平面的一条斜线垂直,那么它也和这条斜线的射影垂直.即
二、专题精讲
题型一 线线、线面、面面垂直关系的综合问题
例题1:为两条不重合的直线,为三个互不重合的平面,给出下面四个命题:
①;②;
;
其中正确的命题有( )
A 1个 B 2个 C 3个 D 4个
【反思小结】与平行问题一样,本题主要考查线线、线面、面面的垂直问题,高考几乎年年都单独考查学生对线面、面面垂直的判定定理和性质定理的准确、深刻的理解,考查学生对符号语言、图形语言、文字语言熟练转换的能力,以选择题、填空题居多,既可能就平行或垂直单独进行考查,又可能在平行中渗透垂直,垂直中兼顾平行,既考查空间想象能力,又考查逻辑推理能力。
拓展练习:设是两条不同的直线,是两个不同的平面,下列命题中正确的是( )
A. B.
C. D.
题型二 线面垂直的定义、判定定理和性质定理及其应用
1.如图,四棱锥P-ABCD中,平面ABCD,,
求证:;
2.如图所示,在长方体中,,M是棱的中点
证明:平面。
3 如图所示,在三棱柱ABC—A1B1C1中,AA1⊥BC,∠A1AC=60°,A1A=AC=BC=1,A1B=.
(1)求证:平面A1BC⊥平面ACC1A1;
(2)如果D为AB中点,求证:BC1∥平面A1CD.
三、学法提炼
证明线线、线面、面面平行或垂直时需要注意以下几点:(1)由已知想性质,由求证想判定,即分析法和综合法相结合寻找解题思路.(2)利用题设条件添加适当的辅助线或辅助面是解题的常用方法之一,例如:证明平行时遇到中点要设法构造中位线或平行四边形,而证明垂直时则要构造等腰三角形的中线、高线、角平分线三线合一;证明线面、面面垂直时要注意条件的充分性,已知线面垂直或面面垂直时要用好性质,构造适当的辅助面.
1.新教材中删去了三垂线定理,用传统方法求角和距离的要求也相当低,教学中不宜过分强调,但是必须明确斜线、垂线、以及斜线在平面内的射影之间的联系,会作出斜线在平面内的射影,从而为线线或线面垂直做好铺垫.
2.线面垂直的性质可以用来证明两条直线垂直和平行,也可以实现面面垂直的证明,因此线面垂直关系是线线垂直、线线平行、面面垂直的枢纽,进而是整个线面位置关系的核心.
3.在线面垂直的定义中,一定要弄清楚不可缺少.
4.面面垂直的性质的理解中三个条仵也不可缺少,即:①两个平面垂直;②其中一个平面内的直线;⑧垂直于交线,所以无论何时见到已知两个平面垂直,都要首先找其交线,看是否存在直线垂直于交线来决定是否该作辅助线,这样就能目标明确,事半功倍.
5.注意充分利用好身边的物体进行比划和举反例,如将课室当成六面体,将书桌、课本、纸张当成平面,笔当成直线等,这些方法依然是解决空间线面位置关系的最佳方法。
1:如图,在四棱锥:中,底面ABCD,,
,E是PC的中点,
证明:(1);(2)平面ABE。
【反思小结】本题考查直线与直线垂直、直线与平面垂直等基础知识,考查空间想象能力和推理论证能力,立体几何的证明关键是学会分析和掌握一些常规的证明方法,如:已知中点证明垂直时要首先考虑等腰三角形中的“三线合一”已知线段或角度等数量关系较多时最好标示出来,充分进行计算,从而发现蕴含的垂直等关系;已知线面垂直时会有哪些结论,是选择线线垂直还是选择面面垂直;要证明结论或要得到哪个结论,就必须满足什么条件等。
2:在四棱锥中,侧棱SA= SC,底面ABCD是菱形,AC与BD交于O点.
(1)求证:平面SBD;
(2)若E为BC的中点,点P在侧面内及其边界上运动,并保持,试指出动点P的转迹,并证明你的结论.
3:如图,AB为圆O的直径,点E、F在圆O上,且,矩形ABCD所在的平面和圆O所在的平面互相垂直,且AB =2,AD =EF=1
(1)求证:平面平面CBF:
(2)设FC的中点为M,求证:平面DAF
(3)设平面CBF将几何体EFABCD分成的两个锥体的体积分别为,求。
学法升华
方法与技巧
1.证明线面垂直的方法
(1)线面垂直的定义:a与α内任何直线都垂直?a⊥α;
(2)判定定理1:?l⊥α;
(3)判定定理2:a∥b,a⊥α?b⊥α;
(4)面面平行的性质:α∥β,a⊥α?a⊥β;
(5)面面垂直的性质:α⊥β,α∩β=l,a?α,a⊥l?a⊥β.
2. 证明线线垂直的方法
(1)定义:两条直线所成的角为90°;
(2)平面几何中证明线线垂直的方法;
(3)线面垂直的性质:a⊥α,b?α?a⊥b;
(4)线面垂直的性质:a⊥α,b∥α?a⊥b.
3. 证明面面垂直的方法
(1)利用定义:两个平面相交,所成的二面角是直二面角;
(2)判定定理:a?α,a⊥β?α⊥β.
失误与防范
1. 垂直关系的转化
在证明两平面垂直时一般先从现有的直线中寻找平面的垂线,若这样的直线图中不存在,则可通过作辅助线来解决.如有平面垂直时,一般要用性质定理,在一个平面内作交线的垂线,使之转化为线面垂直,然后进一步转化为线线垂直.故熟练掌握“线线垂直”、“面面垂直”间的转化条件是解决这类问题的关键.
2.面面垂直的性质定理是作辅助线的一个重要依据.我们要作一个平面的一条垂线,通常是先找这个平面的一个垂面,在这个垂面中,作交线的垂线即可.
课后作业
1.若是互不相同的空间直线,是不重合的两个平面,则下列命题中为真命题的是( )
A.若,则 B.若,则
C.若,则 D.若,则
2.如图,直线PA垂直于以AB为直径的圆所在的平面,C为圆上异于点A和点B的任意一点,有下列四个结论:
①; ; ;
其中不正确的是
3.如图,在正四面体P-ABC中,D、E、F分别是AB、BC、CA的中点,下面四个结论不成立的是 ( )
A.BC∥平面PDF
B.DF⊥平面PAE
C.平面PDF⊥平面PAE
D.平面PDE⊥平面ABC
4.设、β是两个不同的平面,l是一条直线,以下命题正确的是( )
A.若l⊥,⊥β,则l?β B.若l∥,∥β,则l?β
C.若l⊥,∥β,则l⊥β D.若l∥,⊥β,则l⊥β
5.如图所示,在四棱锥P-ABCD中,PA⊥底面ABCD,且底面各边都相等,M是PC上的一动点,当点M满足________时,平面MBD⊥平面PCD.(只要填写一个你认为是正确的条件即可)
6.如图,在直三棱柱ABC-A1B1C1中,AC=3,AB=5, cos∠BAC=.
(1)求证:BC⊥AC1;
(2)若D是AB的中点,求证:AC1∥平面CDB1.
7.如图,在正方体ABCD-A1B1C1D1中,M、N、G分别是A1A,D1C,AD的中点.求证:
(1)MN∥平面ABCD;
(2)MN⊥平面B1BG.
课后小结 上课情况:
课后需再巩固的内容:
组长签字:____________
同课章节目录
