2021年天津市高考数学试卷 (Word解析版)
文档属性
| 名称 | 2021年天津市高考数学试卷 (Word解析版) |  | |
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-14 11:44:50 | ||
图片预览




文档简介
2021年天津市高考数学试卷
一.选择题(共9小题).
1.设集合A={﹣1,0,1},B={1,3,5},C={0,2,4},则(A∩B)∪C=( )
A.{0} B.{0,1,3,5} C.{0,1,2,4} D.{0,2,3,4}
2.已知a∈R,则“a>6”是“a2>36”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
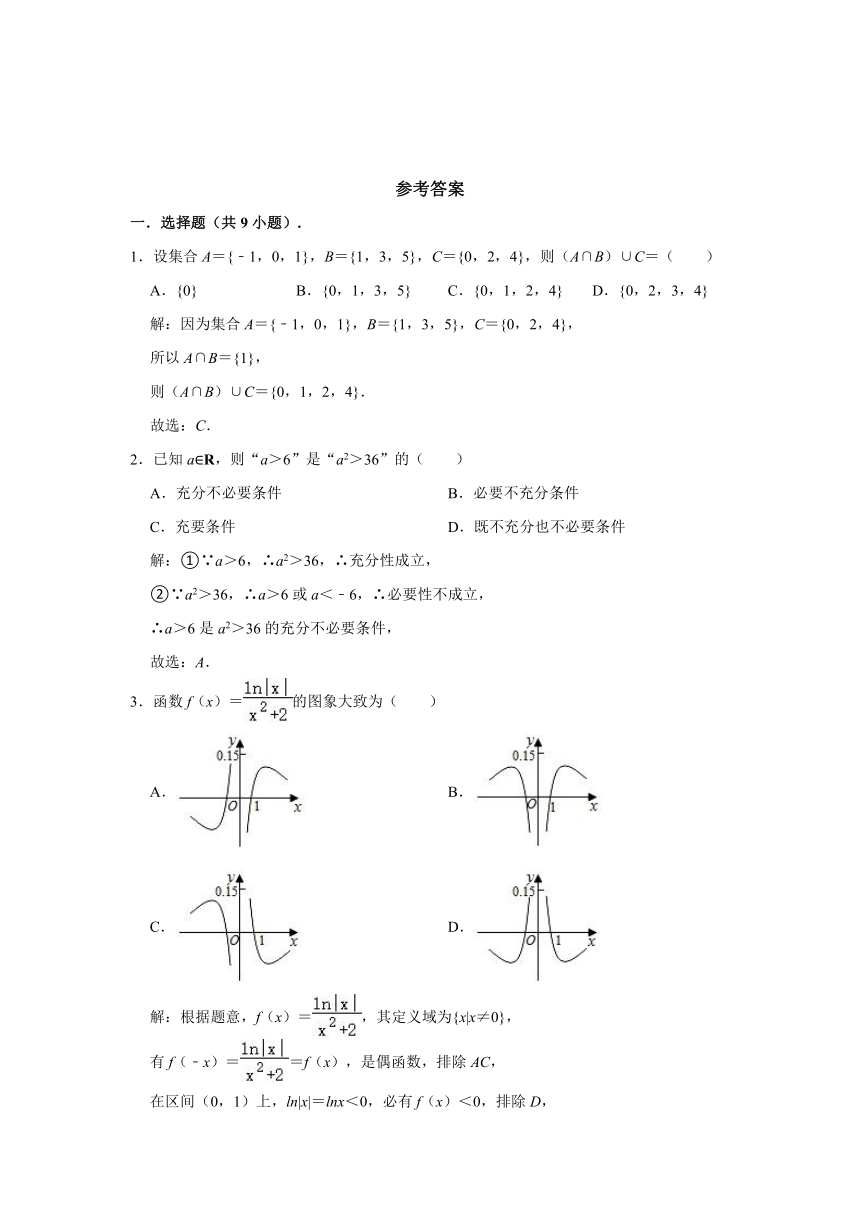
3.函数f(x)=的图象大致为( )
A. B.
C. D.
4.从某网络平台推荐的影视作品中抽取400部,统计其评分数据,将所得400个评分数据分为8组:[66,70),[70,74),…,[94,98),并整理得到如下的频率分布直方图,则评分在区间[82,86)内的影视作品数量是( )
A.20 B.40 C.64 D.80
5.设a=log20.3,b=0.4,c=0.40.3,则三者大小关系为( )
A.a<b<c B.c<a<b C.b<c<a D.a<c<b
6.两个圆锥的底面是一个球的同一截面,顶点均在球面上,若球的体积为,两个圆锥的高之比为1:3,则这两个圆锥的体积之和为( )
A.3π B.4π C.9π D.12π
7.若2a=5b=10,则+=( )
A.﹣1 B.lg7 C.1 D.log710
8.已知双曲线﹣=1(a>0,b>0)的右焦点与抛物线y2=2px(p>0)的焦点重合,抛物线的准线交双曲线于A,B两点,交双曲线的渐近线于C,D两点,若|CD|=|AB|,则双曲线的离心率为( )
A. B. C.2 D.3
9.设a∈R,函数f(x)=,若函数f(x)在区间(0,+∞)内恰有6个零点,则a的取值范围是( )
A.(2,]∪(,] B.(,2]∪(,]
C.(2,]∪[,3) D.(,2)∪[,3)
二.填空题:共6小题,每小题5分,共30分.试题中包含两个空的,答对1个的给3分,全部答对的给5分.
10.i是虚数单位,复数= .
11.在(2x3+)6的展开式中,x6的系数是 .
12.若斜率为的直线与y轴交于点A,与圆x2+(y﹣1)2=1相切于点B,则|AB|= .
13.已知a>0,b>0,则++b的最小值为 .
14.甲、乙两人在每次猜谜活动中各猜一个谜语,若一方猜对且另一方猜错,则猜对的一方获胜,否则本次平局.已知每次活动中,甲、乙猜对的概率分别为和,且每次活动中甲、乙猜对与否互不影响,各次活动也互不影响,则一次活动中,甲获胜的概率为 ;3次活动中,甲至少获胜2次的概率为 .
15.在边长为1的等边三角形ABC中,D为线段BC上的动点,DE⊥AB且交AB于点E,DF∥AB且交AC于点F,则|2+|的值为 ;(+)?的最小值为 .
三.解答题:本大题共5小题,共75分.
16.在△ABC中,内角A,B,C的对边分别为a,b,c,且sinA:sinB:sinC=2:1:,b=.
(1)求a的值;
(2)求cosC的值;
(3)求sin(2C﹣)的值.
17.如图,在棱长为2的正方体ABCD﹣A1B1C1D1中,E,F分别为棱BC,CD的中点.
(1)求证:D1F∥平面A1EC1;
(2)求直线AC1与平面A1EC1所成角的正弦值;
(3)求二面角A﹣A1C1﹣E的正弦值.
18.已知椭圆+=1(a>b)的右焦点为F,上顶点为B,离心率为,且|BF|=.
(1)求椭圆的标准方程;
(2)直线l与椭圆有唯一的公共点M,与y轴的正半轴交于点N,过N与BF垂直的直线交x轴于点P.若MP∥BF,求直线l的方程.
19.已知数列{an}是公差为2的等差数列,其前8项的和为64.数列{bn}是公比大于0的等比数列,b1=4,b3﹣b2=48.
(1)求数列{an}和{bn}的通项公式;
(2)记cn=b2n+,n∈N*.
(i)证明:{cn2﹣c2n}是等比数列;
(ii)证明:<2(n∈N*).
20.(16分)已知a>0,函数f(x)=ax﹣xex.
(1)求曲线f(x)在点(0,f(0))处的切线方程;
(2)证明函数f(x)存在唯一的极值点;
(3)若?a,使得f(x)≤a+b对任意的x∈R恒成立,求实数b的取值范围.
参考答案
一.选择题(共9小题).
1.设集合A={﹣1,0,1},B={1,3,5},C={0,2,4},则(A∩B)∪C=( )
A.{0} B.{0,1,3,5} C.{0,1,2,4} D.{0,2,3,4}
解:因为集合A={﹣1,0,1},B={1,3,5},C={0,2,4},
所以A∩B={1},
则(A∩B)∪C={0,1,2,4}.
故选:C.
2.已知a∈R,则“a>6”是“a2>36”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
解:①∵a>6,∴a2>36,∴充分性成立,
②∵a2>36,∴a>6或a<﹣6,∴必要性不成立,
∴a>6是a2>36的充分不必要条件,
故选:A.
3.函数f(x)=的图象大致为( )
A. B.
C. D.
解:根据题意,f(x)=,其定义域为{x|x≠0},
有f(﹣x)==f(x),是偶函数,排除AC,
在区间(0,1)上,ln|x|=lnx<0,必有f(x)<0,排除D,
故选:B.
4.从某网络平台推荐的影视作品中抽取400部,统计其评分数据,将所得400个评分数据分为8组:[66,70),[70,74),…,[94,98),并整理得到如下的频率分布直方图,则评分在区间[82,86)内的影视作品数量是( )
A.20 B.40 C.64 D.80
解:由频率分布直方图知,
评分在区间[82,86)内的影视作品的频率为(86﹣82)×0.05=0.2,
故评分在区间[82,86)内的影视作品数量是400×0.2=80,
故选:D.
5.设a=log20.3,b=0.4,c=0.40.3,则三者大小关系为( )
A.a<b<c B.c<a<b C.b<c<a D.a<c<b
解:∵log20.3<log21=0,∴a<0,
∵>log0.5=1,∴b>1,
∵0<0.40.3<0.40=1,∴0<c<1,
∴a<c<b,
故选:D.
6.两个圆锥的底面是一个球的同一截面,顶点均在球面上,若球的体积为,两个圆锥的高之比为1:3,则这两个圆锥的体积之和为( )
A.3π B.4π C.9π D.12π
解:如图,设球O的半径为R,由题意,,
可得R=2,则球O的直径为4,
∵两个圆锥的高之比为1:3,∴AO1=1,BO1=3,
由直角三角形中的射影定理可得:r2=1×3,即r=.
∴这两个圆锥的体积之和为V=.
故选:B.
7.若2a=5b=10,则+=( )
A.﹣1 B.lg7 C.1 D.log710
解:∵2a=5b=10,∴a=log210,b=log510,
∴=+=log102+log105=lg10=1,
故选:C.
8.已知双曲线﹣=1(a>0,b>0)的右焦点与抛物线y2=2px(p>0)的焦点重合,抛物线的准线交双曲线于A,B两点,交双曲线的渐近线于C,D两点,若|CD|=|AB|,则双曲线的离心率为( )
A. B. C.2 D.3
【解答】解由题意可得抛物线的准线方程为x=﹣,设AB,CD与x轴分别交于M,N,
由|CD|=|AB|,再由双曲线渐近线及抛物线的对称性可得|CN|=|AM|,
由题意可得:=c,即p=2c,
可得解得:|y|=,所以|AM|=,
可得:|y|=,所以|CN|=,
所以可得=?,可得c=b,
所以c2=2b2=2(c2﹣a2),
解得:c=a,所以双曲线的离心率e==,
故选:A.
9.设a∈R,函数f(x)=,若函数f(x)在区间(0,+∞)内恰有6个零点,则a的取值范围是( )
A.(2,]∪(,] B.(,2]∪(,]
C.(2,]∪[,3) D.(,2)∪[,3)
解:∵f(x)在区间(0,+∞)内恰有6个零点
又∵二次方程最多有两个零点,
∴f(x)=cos(2πx﹣2πa)至少有四个根,
∵f(x)=cos(2πx﹣2πa)=cos2π(x﹣a),
∴令f(x)=0,即 k∈Z,
∴,
又∵x∈(0,+∞),
∴,即,
①当x<a时,﹣6≤﹣5,f(x)有4个零点,即,
﹣7≤﹣6,f(x)有5个零点,即,
﹣8≤﹣7,f(x)有6个零点,即,
②当x≥a时,f(x)=x2﹣2(a+1)x+a2+5,
∴△=b2﹣4ac=4(a+1)2﹣4(a2+5)=8a﹣16=0,解得a=2,
当a<2时,△<0,f(x)无零点,
当a=2时,△=0,f(x)有1个零点,
当a>2时,f(a)=a2﹣2a(a+1)+a2+5=﹣2a+5,
∵f(x)的对称轴x=a+1,即f(a)在对称轴的左边,
∴当﹣2a+5≥0时,即2<a≤,f(x)有两个零点,
当﹣2a+5<0时,即a>,f(x)有1个零点,
综合①②可得,a.
故选:A.
二.填空题:本大题共6小题,每小题5分,共30分.试题中包含两个空的,答对1个的给3分,全部答对的给5分.
10.i是虚数单位,复数= 4﹣i .
解:复数===4﹣i,
故答案为:4﹣i.
11.在(2x3+)6的展开式中,x6的系数是 160 .
解:(2x3+)6的展开式的通项公式为Tr+1=(2x3)6﹣r=26﹣rx18﹣4r,
令18﹣4r=6,解得r=3,
所以x6的系数是23=160.
故答案为:160.
12.若斜率为的直线与y轴交于点A,与圆x2+(y﹣1)2=1相切于点B,则|AB|= .
解:假设A在x轴的上方,斜率为的直线与x轴交于D,
则可得tan∠ADO=,所以cot∠BAC=,如图所示,由圆C的方程可得,圆的半径为|BC|=1,
由于B为切点,所以AB⊥BC,所以|AB|=|BC|?cot∠BAC=,
故答案为:.
13.已知a>0,b>0,则++b的最小值为 2 .
解:∵a>0,b>0,∴++b+b=+b≥2,
当且仅当=且b=,即a=b=时取等号,
∴++b的最小值为 2,
故答案为:2.
14.甲、乙两人在每次猜谜活动中各猜一个谜语,若一方猜对且另一方猜错,则猜对的一方获胜,否则本次平局.已知每次活动中,甲、乙猜对的概率分别为和,且每次活动中甲、乙猜对与否互不影响,各次活动也互不影响,则一次活动中,甲获胜的概率为 ;3次活动中,甲至少获胜2次的概率为 .
解:∵一次活动中,甲获胜的概率为×(1﹣)=,
∴3次活动中,甲至少获胜2次的概率为+××(1﹣)=.
故答案为:,.
15.在边长为1的等边三角形ABC中,D为线段BC上的动点,DE⊥AB且交AB于点E,DF∥AB且交AC于点F,则|2+|的值为 1 ;(+)?的最小值为 .
解:如图,设BE=x,
∵△ABC是边长为1等边三角形,DE⊥AB,
∴∠BDE=30°,BD=2x,DE=x,DC=1﹣2x,
∵DF∥AB,∴△DFC是边长为1﹣2x等边三角形,DE⊥DF,
∴(2+)2=4+4?+=4x2+4x(1﹣2x)×cos0°+(1﹣2x)2=1,
则|2+|=1,
∵(+)?=(+)?(+)=+?
=+(1﹣2x)×(1﹣x)=5x2﹣3x+1
=5+,x∈(0,),
∴(+)?的最小值为.
故答案为:1,.
三.解答题:本大题共5小题,共75分.解答应写出文字说明,证明过程或演算步骤.
16.在△ABC中,内角A,B,C的对边分别为a,b,c,且sinA:sinB:sinC=2:1:,b=.
(1)求a的值;
(2)求cosC的值;
(3)求sin(2C﹣)的值.
解:(1)∵△ABC中,sinA:sinB:sinC=2:1:,∴a:b:c=2:1:,
∵b=,∴a=2b=2,c=b=2.
(2)△ABC中,由余弦定理可得cosC===.
(3)由(2)可得sinC==,
∴sin2C=2sinCcosC=,cos2C=2cos2C﹣1=,
sin(2C﹣)=sin2Ccos﹣cos2Csin=.
17.如图,在棱长为2的正方体ABCD﹣A1B1C1D1中,E,F分别为棱BC,CD的中点.
(1)求证:D1F∥平面A1EC1;
(2)求直线AC1与平面A1EC1所成角的正弦值;
(3)求二面角A﹣A1C1﹣E的正弦值.
【解答】(1)证明:以点A为坐标原点,建立空间直角坐标系如图所示,
则A1(0,0,2),E(2,1,0),C1(2,2,2),
故,
设平面A1EC1的法向量为,
则,即,
令z=1,则x=2,y=﹣2,故,
又F(1,2,0),D1(0,2,2),
所以,
则,又D1F?平面A1EC,
故D1F//平面A1EC1;
(2)解:由(1)可知,,
则==,
故直线AC1与平面A1EC1所成角的正弦值为;
(3)解:由(1)可知,,
设平面AA1C1的法向量为,
则,即,
令a=1,则b=﹣1,故,
所以=,
故二面角A﹣A1C1﹣E的正弦值为=.
18.已知椭圆+=1(a>b)的右焦点为F,上顶点为B,离心率为,且|BF|=.
(1)求椭圆的标准方程;
(2)直线l与椭圆有唯一的公共点M,与y轴的正半轴交于点N,过N与BF垂直的直线交x轴于点P.若MP∥BF,求直线l的方程.
解:(1)因为离心率e=,|BF|=,
所以,解得a=,c=2,b=1,
所以椭圆的方程为+y2=1.
(2)设M(x0,y0),
则切线MN的方程为+y0y=1,
令x=0,得yN=,
因为PN⊥BF,
所以kPN?kBF=﹣1,
所以kPN?(﹣)=﹣1,解得kNP=2,
设P(x1,0),则kNP==2,即x1=﹣,
因为MP∥BF,
所以kMP=kBF,
所以=﹣,即﹣2y0=x0+,
所以x0=﹣2y0﹣,
又因为+y02=1,
所以+++y02=1,
解得y0=±,
因为yN>0,
所以y0>0,
所以y0=,x0=﹣﹣=﹣,
所以+y=1,即x﹣y+=0.
19.已知数列{an}是公差为2的等差数列,其前8项的和为64.数列{bn}是公比大于0的等比数列,b1=4,b3﹣b2=48.
(1)求数列{an}和{bn}的通项公式;
(2)记cn=b2n+,n∈N*.
(i)证明:{cn2﹣c2n}是等比数列;
(ii)证明:<2(n∈N*).
【解答】证明:(1)由数列{an}是公差d为2的等差数列,其前8项的和为64,
可得8a1+×8×7d=64,解得a1=1,
所以an=1+2(n﹣1)=2n﹣1;
由数列{bn}是公比q大于0的等比数列,b1=4,b3﹣b2=48,
可得4q2﹣4q=48,解得q=4(﹣3舍去),
所以bn=4n;
(2)(i)证明:因为an=2n﹣1,bn=4n,
所以cn=b2n+=42n+,
则cn2﹣c2n=(42n+)2﹣(44n+)==2?4n,
所以,
又,
所以数列{cn2﹣c2n}是以8为首项,4为公比的等比数列;
(ii)证明:设=,
考虑,则pn<qn,
所以qk=++...+,
则,
两式相减可得,==,
所以,
则<<2,
故<2.
20.(16分)已知a>0,函数f(x)=ax﹣xex.
(1)求曲线f(x)在点(0,f(0))处的切线方程;
(2)证明函数f(x)存在唯一的极值点;
(3)若?a,使得f(x)≤a+b对任意的x∈R恒成立,求实数b的取值范围.
【解答】(1)解:因为f'(x)=a﹣(x+1)ex,所以f'(0)=a﹣1,而f(0)=0,
所以在(0,f(0))处的切线方程为y=(a﹣1)x(a>0);
(2)证明:令f'(x)=a﹣(x+1)ex=0,则a=(x+1)ex,
令g(x)=(x+1)ex,则g'(x)=(x+2)ex,令g'(x)=0,解得x=﹣2,
当x∈(﹣∞,﹣2)时,g'(x)<0,g(x)单调递减,
当x∈(﹣2,+∞)时,g'(x)>0,g(x)单调递增,
当x→﹣∞时,g(x)<0,当x→+∞时,g(x)>0,
作出图象
所以当a>0时,y=a与y=g(x)仅有一个交点,令g(m)=a,
则m>﹣1,且f(m)=a﹣g(m)=0,
当x∈(﹣∞,m)时,a>g(m),f'(x)>0,f(x)为增函数;
当x∈(m,+∞)时,a<g(m),f'(x)<0,f(x)为减函数;
所以x=m时f(x)的极大值点,故f(x)仅有一个极值点;
(3)解:由(2)知f(x)max=f(m),
此时a=(1+m)em,(m>﹣1),
所以{f(x)﹣a}max=f(m)﹣a=(1+m)em﹣m﹣mem﹣(1+m)em=(m2﹣m﹣1)em(m>﹣1),
令h(x)=(x2﹣x﹣1)ex(x>﹣1),
若存在a,使f(x)≤a+b对任意的x∈R恒成立,
则等价于存在x∈(﹣1,+∞),使得h(x)≤b,即b≥h(x)min,
而h'(x)=(x2+x﹣2)ex=(x﹣1)(x+2)ex,(x>﹣1),
当x∈(﹣1,1)时,h'(x)<0,h(x)为单调减函数,
当x∈(1,+∞)时,h'(x)>0,h(x)为单调增函数,
所以h(x)min=h(1)=﹣e,故b≥﹣e,
所以实数b的取值范围[﹣e,+∞).
一.选择题(共9小题).
1.设集合A={﹣1,0,1},B={1,3,5},C={0,2,4},则(A∩B)∪C=( )
A.{0} B.{0,1,3,5} C.{0,1,2,4} D.{0,2,3,4}
2.已知a∈R,则“a>6”是“a2>36”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
3.函数f(x)=的图象大致为( )
A. B.
C. D.
4.从某网络平台推荐的影视作品中抽取400部,统计其评分数据,将所得400个评分数据分为8组:[66,70),[70,74),…,[94,98),并整理得到如下的频率分布直方图,则评分在区间[82,86)内的影视作品数量是( )
A.20 B.40 C.64 D.80
5.设a=log20.3,b=0.4,c=0.40.3,则三者大小关系为( )
A.a<b<c B.c<a<b C.b<c<a D.a<c<b
6.两个圆锥的底面是一个球的同一截面,顶点均在球面上,若球的体积为,两个圆锥的高之比为1:3,则这两个圆锥的体积之和为( )
A.3π B.4π C.9π D.12π
7.若2a=5b=10,则+=( )
A.﹣1 B.lg7 C.1 D.log710
8.已知双曲线﹣=1(a>0,b>0)的右焦点与抛物线y2=2px(p>0)的焦点重合,抛物线的准线交双曲线于A,B两点,交双曲线的渐近线于C,D两点,若|CD|=|AB|,则双曲线的离心率为( )
A. B. C.2 D.3
9.设a∈R,函数f(x)=,若函数f(x)在区间(0,+∞)内恰有6个零点,则a的取值范围是( )
A.(2,]∪(,] B.(,2]∪(,]
C.(2,]∪[,3) D.(,2)∪[,3)
二.填空题:共6小题,每小题5分,共30分.试题中包含两个空的,答对1个的给3分,全部答对的给5分.
10.i是虚数单位,复数= .
11.在(2x3+)6的展开式中,x6的系数是 .
12.若斜率为的直线与y轴交于点A,与圆x2+(y﹣1)2=1相切于点B,则|AB|= .
13.已知a>0,b>0,则++b的最小值为 .
14.甲、乙两人在每次猜谜活动中各猜一个谜语,若一方猜对且另一方猜错,则猜对的一方获胜,否则本次平局.已知每次活动中,甲、乙猜对的概率分别为和,且每次活动中甲、乙猜对与否互不影响,各次活动也互不影响,则一次活动中,甲获胜的概率为 ;3次活动中,甲至少获胜2次的概率为 .
15.在边长为1的等边三角形ABC中,D为线段BC上的动点,DE⊥AB且交AB于点E,DF∥AB且交AC于点F,则|2+|的值为 ;(+)?的最小值为 .
三.解答题:本大题共5小题,共75分.
16.在△ABC中,内角A,B,C的对边分别为a,b,c,且sinA:sinB:sinC=2:1:,b=.
(1)求a的值;
(2)求cosC的值;
(3)求sin(2C﹣)的值.
17.如图,在棱长为2的正方体ABCD﹣A1B1C1D1中,E,F分别为棱BC,CD的中点.
(1)求证:D1F∥平面A1EC1;
(2)求直线AC1与平面A1EC1所成角的正弦值;
(3)求二面角A﹣A1C1﹣E的正弦值.
18.已知椭圆+=1(a>b)的右焦点为F,上顶点为B,离心率为,且|BF|=.
(1)求椭圆的标准方程;
(2)直线l与椭圆有唯一的公共点M,与y轴的正半轴交于点N,过N与BF垂直的直线交x轴于点P.若MP∥BF,求直线l的方程.
19.已知数列{an}是公差为2的等差数列,其前8项的和为64.数列{bn}是公比大于0的等比数列,b1=4,b3﹣b2=48.
(1)求数列{an}和{bn}的通项公式;
(2)记cn=b2n+,n∈N*.
(i)证明:{cn2﹣c2n}是等比数列;
(ii)证明:<2(n∈N*).
20.(16分)已知a>0,函数f(x)=ax﹣xex.
(1)求曲线f(x)在点(0,f(0))处的切线方程;
(2)证明函数f(x)存在唯一的极值点;
(3)若?a,使得f(x)≤a+b对任意的x∈R恒成立,求实数b的取值范围.
参考答案
一.选择题(共9小题).
1.设集合A={﹣1,0,1},B={1,3,5},C={0,2,4},则(A∩B)∪C=( )
A.{0} B.{0,1,3,5} C.{0,1,2,4} D.{0,2,3,4}
解:因为集合A={﹣1,0,1},B={1,3,5},C={0,2,4},
所以A∩B={1},
则(A∩B)∪C={0,1,2,4}.
故选:C.
2.已知a∈R,则“a>6”是“a2>36”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
解:①∵a>6,∴a2>36,∴充分性成立,
②∵a2>36,∴a>6或a<﹣6,∴必要性不成立,
∴a>6是a2>36的充分不必要条件,
故选:A.
3.函数f(x)=的图象大致为( )
A. B.
C. D.
解:根据题意,f(x)=,其定义域为{x|x≠0},
有f(﹣x)==f(x),是偶函数,排除AC,
在区间(0,1)上,ln|x|=lnx<0,必有f(x)<0,排除D,
故选:B.
4.从某网络平台推荐的影视作品中抽取400部,统计其评分数据,将所得400个评分数据分为8组:[66,70),[70,74),…,[94,98),并整理得到如下的频率分布直方图,则评分在区间[82,86)内的影视作品数量是( )
A.20 B.40 C.64 D.80
解:由频率分布直方图知,
评分在区间[82,86)内的影视作品的频率为(86﹣82)×0.05=0.2,
故评分在区间[82,86)内的影视作品数量是400×0.2=80,
故选:D.
5.设a=log20.3,b=0.4,c=0.40.3,则三者大小关系为( )
A.a<b<c B.c<a<b C.b<c<a D.a<c<b
解:∵log20.3<log21=0,∴a<0,
∵>log0.5=1,∴b>1,
∵0<0.40.3<0.40=1,∴0<c<1,
∴a<c<b,
故选:D.
6.两个圆锥的底面是一个球的同一截面,顶点均在球面上,若球的体积为,两个圆锥的高之比为1:3,则这两个圆锥的体积之和为( )
A.3π B.4π C.9π D.12π
解:如图,设球O的半径为R,由题意,,
可得R=2,则球O的直径为4,
∵两个圆锥的高之比为1:3,∴AO1=1,BO1=3,
由直角三角形中的射影定理可得:r2=1×3,即r=.
∴这两个圆锥的体积之和为V=.
故选:B.
7.若2a=5b=10,则+=( )
A.﹣1 B.lg7 C.1 D.log710
解:∵2a=5b=10,∴a=log210,b=log510,
∴=+=log102+log105=lg10=1,
故选:C.
8.已知双曲线﹣=1(a>0,b>0)的右焦点与抛物线y2=2px(p>0)的焦点重合,抛物线的准线交双曲线于A,B两点,交双曲线的渐近线于C,D两点,若|CD|=|AB|,则双曲线的离心率为( )
A. B. C.2 D.3
【解答】解由题意可得抛物线的准线方程为x=﹣,设AB,CD与x轴分别交于M,N,
由|CD|=|AB|,再由双曲线渐近线及抛物线的对称性可得|CN|=|AM|,
由题意可得:=c,即p=2c,
可得解得:|y|=,所以|AM|=,
可得:|y|=,所以|CN|=,
所以可得=?,可得c=b,
所以c2=2b2=2(c2﹣a2),
解得:c=a,所以双曲线的离心率e==,
故选:A.
9.设a∈R,函数f(x)=,若函数f(x)在区间(0,+∞)内恰有6个零点,则a的取值范围是( )
A.(2,]∪(,] B.(,2]∪(,]
C.(2,]∪[,3) D.(,2)∪[,3)
解:∵f(x)在区间(0,+∞)内恰有6个零点
又∵二次方程最多有两个零点,
∴f(x)=cos(2πx﹣2πa)至少有四个根,
∵f(x)=cos(2πx﹣2πa)=cos2π(x﹣a),
∴令f(x)=0,即 k∈Z,
∴,
又∵x∈(0,+∞),
∴,即,
①当x<a时,﹣6≤﹣5,f(x)有4个零点,即,
﹣7≤﹣6,f(x)有5个零点,即,
﹣8≤﹣7,f(x)有6个零点,即,
②当x≥a时,f(x)=x2﹣2(a+1)x+a2+5,
∴△=b2﹣4ac=4(a+1)2﹣4(a2+5)=8a﹣16=0,解得a=2,
当a<2时,△<0,f(x)无零点,
当a=2时,△=0,f(x)有1个零点,
当a>2时,f(a)=a2﹣2a(a+1)+a2+5=﹣2a+5,
∵f(x)的对称轴x=a+1,即f(a)在对称轴的左边,
∴当﹣2a+5≥0时,即2<a≤,f(x)有两个零点,
当﹣2a+5<0时,即a>,f(x)有1个零点,
综合①②可得,a.
故选:A.
二.填空题:本大题共6小题,每小题5分,共30分.试题中包含两个空的,答对1个的给3分,全部答对的给5分.
10.i是虚数单位,复数= 4﹣i .
解:复数===4﹣i,
故答案为:4﹣i.
11.在(2x3+)6的展开式中,x6的系数是 160 .
解:(2x3+)6的展开式的通项公式为Tr+1=(2x3)6﹣r=26﹣rx18﹣4r,
令18﹣4r=6,解得r=3,
所以x6的系数是23=160.
故答案为:160.
12.若斜率为的直线与y轴交于点A,与圆x2+(y﹣1)2=1相切于点B,则|AB|= .
解:假设A在x轴的上方,斜率为的直线与x轴交于D,
则可得tan∠ADO=,所以cot∠BAC=,如图所示,由圆C的方程可得,圆的半径为|BC|=1,
由于B为切点,所以AB⊥BC,所以|AB|=|BC|?cot∠BAC=,
故答案为:.
13.已知a>0,b>0,则++b的最小值为 2 .
解:∵a>0,b>0,∴++b+b=+b≥2,
当且仅当=且b=,即a=b=时取等号,
∴++b的最小值为 2,
故答案为:2.
14.甲、乙两人在每次猜谜活动中各猜一个谜语,若一方猜对且另一方猜错,则猜对的一方获胜,否则本次平局.已知每次活动中,甲、乙猜对的概率分别为和,且每次活动中甲、乙猜对与否互不影响,各次活动也互不影响,则一次活动中,甲获胜的概率为 ;3次活动中,甲至少获胜2次的概率为 .
解:∵一次活动中,甲获胜的概率为×(1﹣)=,
∴3次活动中,甲至少获胜2次的概率为+××(1﹣)=.
故答案为:,.
15.在边长为1的等边三角形ABC中,D为线段BC上的动点,DE⊥AB且交AB于点E,DF∥AB且交AC于点F,则|2+|的值为 1 ;(+)?的最小值为 .
解:如图,设BE=x,
∵△ABC是边长为1等边三角形,DE⊥AB,
∴∠BDE=30°,BD=2x,DE=x,DC=1﹣2x,
∵DF∥AB,∴△DFC是边长为1﹣2x等边三角形,DE⊥DF,
∴(2+)2=4+4?+=4x2+4x(1﹣2x)×cos0°+(1﹣2x)2=1,
则|2+|=1,
∵(+)?=(+)?(+)=+?
=+(1﹣2x)×(1﹣x)=5x2﹣3x+1
=5+,x∈(0,),
∴(+)?的最小值为.
故答案为:1,.
三.解答题:本大题共5小题,共75分.解答应写出文字说明,证明过程或演算步骤.
16.在△ABC中,内角A,B,C的对边分别为a,b,c,且sinA:sinB:sinC=2:1:,b=.
(1)求a的值;
(2)求cosC的值;
(3)求sin(2C﹣)的值.
解:(1)∵△ABC中,sinA:sinB:sinC=2:1:,∴a:b:c=2:1:,
∵b=,∴a=2b=2,c=b=2.
(2)△ABC中,由余弦定理可得cosC===.
(3)由(2)可得sinC==,
∴sin2C=2sinCcosC=,cos2C=2cos2C﹣1=,
sin(2C﹣)=sin2Ccos﹣cos2Csin=.
17.如图,在棱长为2的正方体ABCD﹣A1B1C1D1中,E,F分别为棱BC,CD的中点.
(1)求证:D1F∥平面A1EC1;
(2)求直线AC1与平面A1EC1所成角的正弦值;
(3)求二面角A﹣A1C1﹣E的正弦值.
【解答】(1)证明:以点A为坐标原点,建立空间直角坐标系如图所示,
则A1(0,0,2),E(2,1,0),C1(2,2,2),
故,
设平面A1EC1的法向量为,
则,即,
令z=1,则x=2,y=﹣2,故,
又F(1,2,0),D1(0,2,2),
所以,
则,又D1F?平面A1EC,
故D1F//平面A1EC1;
(2)解:由(1)可知,,
则==,
故直线AC1与平面A1EC1所成角的正弦值为;
(3)解:由(1)可知,,
设平面AA1C1的法向量为,
则,即,
令a=1,则b=﹣1,故,
所以=,
故二面角A﹣A1C1﹣E的正弦值为=.
18.已知椭圆+=1(a>b)的右焦点为F,上顶点为B,离心率为,且|BF|=.
(1)求椭圆的标准方程;
(2)直线l与椭圆有唯一的公共点M,与y轴的正半轴交于点N,过N与BF垂直的直线交x轴于点P.若MP∥BF,求直线l的方程.
解:(1)因为离心率e=,|BF|=,
所以,解得a=,c=2,b=1,
所以椭圆的方程为+y2=1.
(2)设M(x0,y0),
则切线MN的方程为+y0y=1,
令x=0,得yN=,
因为PN⊥BF,
所以kPN?kBF=﹣1,
所以kPN?(﹣)=﹣1,解得kNP=2,
设P(x1,0),则kNP==2,即x1=﹣,
因为MP∥BF,
所以kMP=kBF,
所以=﹣,即﹣2y0=x0+,
所以x0=﹣2y0﹣,
又因为+y02=1,
所以+++y02=1,
解得y0=±,
因为yN>0,
所以y0>0,
所以y0=,x0=﹣﹣=﹣,
所以+y=1,即x﹣y+=0.
19.已知数列{an}是公差为2的等差数列,其前8项的和为64.数列{bn}是公比大于0的等比数列,b1=4,b3﹣b2=48.
(1)求数列{an}和{bn}的通项公式;
(2)记cn=b2n+,n∈N*.
(i)证明:{cn2﹣c2n}是等比数列;
(ii)证明:<2(n∈N*).
【解答】证明:(1)由数列{an}是公差d为2的等差数列,其前8项的和为64,
可得8a1+×8×7d=64,解得a1=1,
所以an=1+2(n﹣1)=2n﹣1;
由数列{bn}是公比q大于0的等比数列,b1=4,b3﹣b2=48,
可得4q2﹣4q=48,解得q=4(﹣3舍去),
所以bn=4n;
(2)(i)证明:因为an=2n﹣1,bn=4n,
所以cn=b2n+=42n+,
则cn2﹣c2n=(42n+)2﹣(44n+)==2?4n,
所以,
又,
所以数列{cn2﹣c2n}是以8为首项,4为公比的等比数列;
(ii)证明:设=,
考虑,则pn<qn,
所以qk=++...+,
则,
两式相减可得,==,
所以,
则<<2,
故<2.
20.(16分)已知a>0,函数f(x)=ax﹣xex.
(1)求曲线f(x)在点(0,f(0))处的切线方程;
(2)证明函数f(x)存在唯一的极值点;
(3)若?a,使得f(x)≤a+b对任意的x∈R恒成立,求实数b的取值范围.
【解答】(1)解:因为f'(x)=a﹣(x+1)ex,所以f'(0)=a﹣1,而f(0)=0,
所以在(0,f(0))处的切线方程为y=(a﹣1)x(a>0);
(2)证明:令f'(x)=a﹣(x+1)ex=0,则a=(x+1)ex,
令g(x)=(x+1)ex,则g'(x)=(x+2)ex,令g'(x)=0,解得x=﹣2,
当x∈(﹣∞,﹣2)时,g'(x)<0,g(x)单调递减,
当x∈(﹣2,+∞)时,g'(x)>0,g(x)单调递增,
当x→﹣∞时,g(x)<0,当x→+∞时,g(x)>0,
作出图象
所以当a>0时,y=a与y=g(x)仅有一个交点,令g(m)=a,
则m>﹣1,且f(m)=a﹣g(m)=0,
当x∈(﹣∞,m)时,a>g(m),f'(x)>0,f(x)为增函数;
当x∈(m,+∞)时,a<g(m),f'(x)<0,f(x)为减函数;
所以x=m时f(x)的极大值点,故f(x)仅有一个极值点;
(3)解:由(2)知f(x)max=f(m),
此时a=(1+m)em,(m>﹣1),
所以{f(x)﹣a}max=f(m)﹣a=(1+m)em﹣m﹣mem﹣(1+m)em=(m2﹣m﹣1)em(m>﹣1),
令h(x)=(x2﹣x﹣1)ex(x>﹣1),
若存在a,使f(x)≤a+b对任意的x∈R恒成立,
则等价于存在x∈(﹣1,+∞),使得h(x)≤b,即b≥h(x)min,
而h'(x)=(x2+x﹣2)ex=(x﹣1)(x+2)ex,(x>﹣1),
当x∈(﹣1,1)时,h'(x)<0,h(x)为单调减函数,
当x∈(1,+∞)时,h'(x)>0,h(x)为单调增函数,
所以h(x)min=h(1)=﹣e,故b≥﹣e,
所以实数b的取值范围[﹣e,+∞).
同课章节目录
