2022届高考数学一轮复习诱导公式和三角函数的图像和性质教案
文档属性
| 名称 | 2022届高考数学一轮复习诱导公式和三角函数的图像和性质教案 |  | |
| 格式 | docx | ||
| 文件大小 | 453.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-17 21:11:03 | ||
图片预览




文档简介
学习目标
明确三角函数诱导公式的来龙去脉,理解诱导公式的推导过程;
培养逻辑推理能力及运算能力,渗透转化及分类讨论的思想.
3.
理解正弦函数、余弦函数图象的画法.借助图象变换,了解函数之间的内在联系.通过三角函数图象的三种画法
诱导公式和三角函数的图像和性质
学习难重点
过诱导公式的具体运用,熟练正确地运用公式解决一些三角函数的求值?化简和证明问题,体会公式变形在数学中的作用.
2.理解周期函数与最小正周期的意义,会求三角函数的最小正周期.
3.理解正弦函数、余弦函数奇偶性、单调性、最大值与最小值的概念.
知识点:
一?诱导公式一
终边相同角的同一三角函数的值相等,即
sin(α+k·2π)=
sinα
;
cos(α+k·2π)=cos
α;
tan(α+k·2π)=tanα,其中k∈Z.
二?诱导公式二?三?四
1.诱导公式二
(1)角π+α与角α的终边关于原点对称.
如图所示.
(2)公式:sin(π+α)=-
sinα.cos(π+α)=
cos
α .tan(π+α)=
tanα.
2.诱导公式三
(1)角-α与角α的终边关于x轴对称.
如图所示.
(2)公式:sin(-α)=
-
sinα.cos(-α)=
cos
α
.tan(-α)=-
tanα.
3.诱导公式四
(1)角π-α与角α终边关于y轴对称.如图所示.
(2)公式:sin(π-α)=
sinα.cos(π-α)=
-cos
α.tan(π-α)=
-
tanα..
三?诱导公式五?六
1.公式五?六
设任意角的终边与单位圆的交点坐标为,由于角的终边与角的终边关于直线y=x对称,角的终边与单位圆的交点与点关于直线对称,因此点的坐标是(如图所示).
由三角函数的定义得:
,;,.
从而可得:
公式五
cos
α,
sinα.
由于,由公式四及公式五可得:
公式六
cos
α,
-sinα.
三角函数图象和性质
一、正弦函数图象
1.正弦函数的图象
二、余弦函数图象
1.余弦函数的图象
三、正切函数图象
四、正余弦函数的性质
1.周期函数
(1)对于函数f(x),如果存在一个非零常数T,使得当x取定义域内的每一个值时,都有f(x+T)=f(x)那么函数f(x)就叫做周期函数,非零常数T叫做这个函数的周期.
(2)如果在周期函数f(x)的所有周期中存在一个最小的正数,那么这个最小正数就叫做f(x)的最小正周期.
(3)正弦函数y=sinx(x∈R)和余弦函数y=cosx(x∈R)都是周期函数,最小正周期为,2kπ(且k≠0)是它们的周期.
2.正弦函数、余弦函数的性质
函数
y=sinx
y=cosx
定义域
R
值域
[-1,1]
图象
奇偶性
奇函数
偶函数
周期性
最小正周期:T=2π
单调性
在(k∈Z)上递增;
在(k∈Z)上递减
在(k∈Z)上递增;
在(k∈Z)上递减
最值
当x=时,ymin=-1;
当x=时,ymax=1
当x=时,ymin=-1;
当x=时,ymax=1
对称轴
x=+kπ,k∈Z
x=kπ,k∈Z
对称
中心
(kπ,0),k∈Z
(+kπ,0),k∈Z
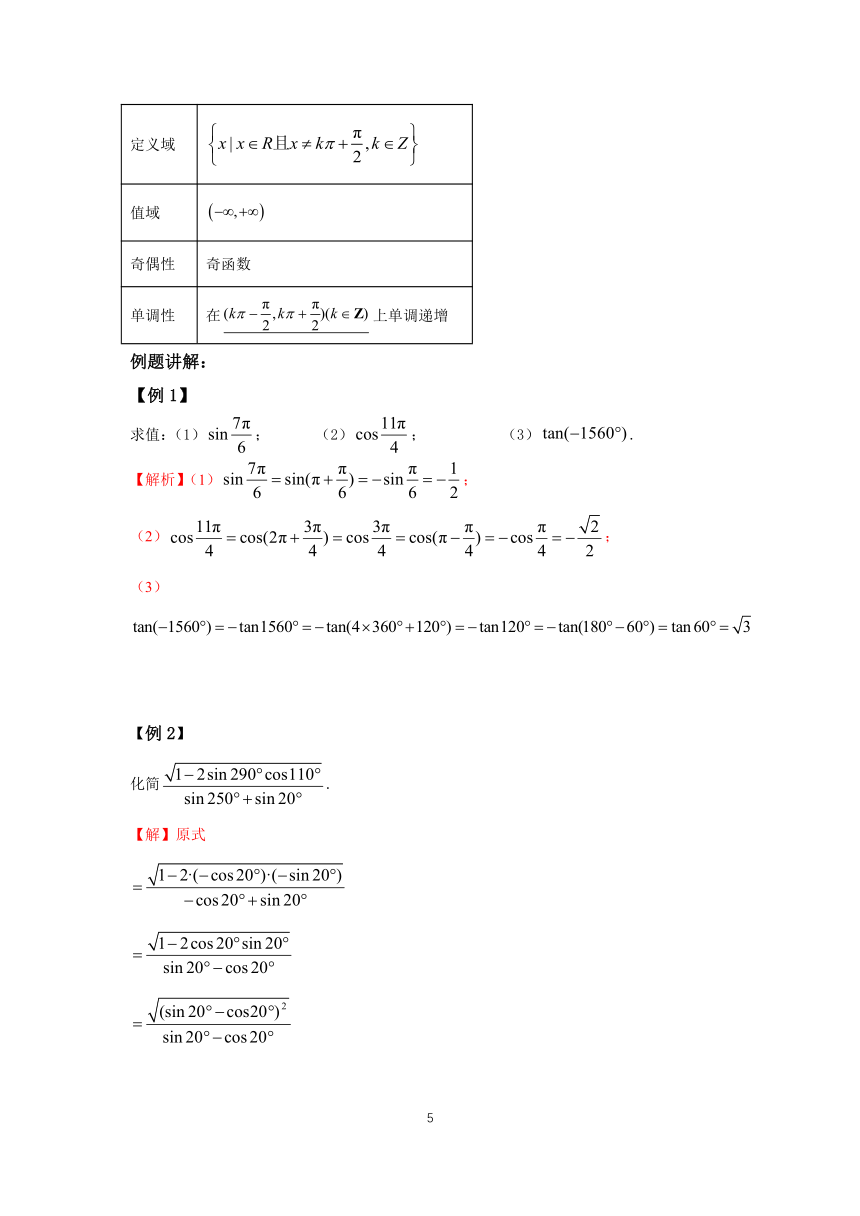
五、正切函数的性质
定义域
值域
奇偶性
奇函数
单调性
在上单调递增
例题讲解:
【例1】
求值:(1);
(2);
(3).
【解析】(1);
(2);
(3)
【例2】
化简.
【解】原式
.
【例3】
图中的曲线对应的函数解析式是(
)
A.
B.
C.
D.
【答案】D
【例4】
在上使成立的的取值范围是(
)
A.
B.
C.
D.
【答案】A
【解析】
【分析】由,可得,利用正弦函数的性质得的范围,又因为,再赋值求出即可.
【详解】
,
,
,
又因为,所以当时,,
当时,,
综上:
【例5】
下列函数中,周期为的是(
)
A.
y=sin
B.
y=sin2x
C.
y=cos
D.
y=cos(-4x)
【答案】D
【解析】
【分析】
根据周期公式求解即可.
【详解】根据公式
的周期为,故A错误;
的周期为,故B错误;
的周期为,故C错误;
的周期为,故D正确;
【例6】
函数的最大值是(
)
A.
B.
C.
D.
【答案】C
【解析】
【分析】结合同角三角函数的基本关系式、二次函数的性质,求得函数的最大值.
【详解】
,
当时等号成立,
所以函数的最大值是.
故选:C
课堂运用
1._______.
【答案】
【解析】
2.已知,求的值.
【解】原式
.
3.
函数,,则的范围是(
)
A.
B.
C.
D.
【答案】C
【解析】
【分析】根据正弦函数的单调性直接求解即可.
【详解】根据正弦函数图象可知在区间上,函数先增后减,
当时,,当时,.
故选:C.
4.
函数的简图是(
)
A.
B.
C.
D.
【答案】D
【解析】
【分析】
利用余弦函数的图象平移可得.
【详解】把的图象向上平移1个单位即可.
故选:D
5.
函数的最小正周期是(
)
A.
B.
C.
D.
4
【答案】B
【解析】
【分析】
直接利用周期公式求解即可
【详解】,由周期公式.
6.
函数f(x)=在[—π,π]的图像大致为
A.
B.
C.
D.
【答案】D
【解析】
【分析】先判断函数的奇偶性,得是奇函数,排除A,再注意到选项的区别,利用特殊值得正确答案.
【详解】由,得是奇函数,其图象关于原点对称.又.故选D.
7.
设函数在的图像大致如下图,则f(x)的最小正周期为(
)
A.
B.
C.
D.
【答案】C
【解析】
【分析】由图可得:函数图象过点,即可得到,结合是函数图象与轴负半轴的第一个交点即可得到,即可求得,再利用三角函数周期公式即可得解.
【详解】由图可得:函数图象过点,
将它代入函数可得:
又是函数图象与轴负半轴的第一个交点,
所以,解得:
所以函数的最小正周期为
故选:C
8.
已知向量.
(1)若,求x的值;
(2)记,求函数y=f(x)的最大值和最小值及对应的x的值.
【答案】(1)(2)时,取到最大值3;
时,取到最小值.
【解析】
【分析】(1)根据,利用向量平行的充要条件建立等式,即可求x的值.
(2)根据求解求函数y=f(x)解析式,化简,结合三角函数的性质即可求解最大值和最小值及对应的x的值.
【详解】解:(1)∵向量.
由,
可得:,
即,
∵x∈[0,π]
∴.
(2)由
∵x∈[0,π],
∴
∴当时,即x=0时f(x)max=3;
当,即时.
课后作业:
1.已知函数.
(I)求f(x)的最小正周期;
(II)求证:当时,.
【答案】(1)(2)见解析
【解析】
【详解】试题分析:(Ⅰ)首先根据两角差的余弦公式化简,再根据辅助角公式化简为,最后根据公式求周期;(Ⅱ)先求的范围再求函数的最小值.
试题解析:(Ⅰ).
所以的最小正周期.
(Ⅱ)因为,
所以.
所以.
所以当时,.
2
明确三角函数诱导公式的来龙去脉,理解诱导公式的推导过程;
培养逻辑推理能力及运算能力,渗透转化及分类讨论的思想.
3.
理解正弦函数、余弦函数图象的画法.借助图象变换,了解函数之间的内在联系.通过三角函数图象的三种画法
诱导公式和三角函数的图像和性质
学习难重点
过诱导公式的具体运用,熟练正确地运用公式解决一些三角函数的求值?化简和证明问题,体会公式变形在数学中的作用.
2.理解周期函数与最小正周期的意义,会求三角函数的最小正周期.
3.理解正弦函数、余弦函数奇偶性、单调性、最大值与最小值的概念.
知识点:
一?诱导公式一
终边相同角的同一三角函数的值相等,即
sin(α+k·2π)=
sinα
;
cos(α+k·2π)=cos
α;
tan(α+k·2π)=tanα,其中k∈Z.
二?诱导公式二?三?四
1.诱导公式二
(1)角π+α与角α的终边关于原点对称.
如图所示.
(2)公式:sin(π+α)=-
sinα.cos(π+α)=
cos
α .tan(π+α)=
tanα.
2.诱导公式三
(1)角-α与角α的终边关于x轴对称.
如图所示.
(2)公式:sin(-α)=
-
sinα.cos(-α)=
cos
α
.tan(-α)=-
tanα.
3.诱导公式四
(1)角π-α与角α终边关于y轴对称.如图所示.
(2)公式:sin(π-α)=
sinα.cos(π-α)=
-cos
α.tan(π-α)=
-
tanα..
三?诱导公式五?六
1.公式五?六
设任意角的终边与单位圆的交点坐标为,由于角的终边与角的终边关于直线y=x对称,角的终边与单位圆的交点与点关于直线对称,因此点的坐标是(如图所示).
由三角函数的定义得:
,;,.
从而可得:
公式五
cos
α,
sinα.
由于,由公式四及公式五可得:
公式六
cos
α,
-sinα.
三角函数图象和性质
一、正弦函数图象
1.正弦函数的图象
二、余弦函数图象
1.余弦函数的图象
三、正切函数图象
四、正余弦函数的性质
1.周期函数
(1)对于函数f(x),如果存在一个非零常数T,使得当x取定义域内的每一个值时,都有f(x+T)=f(x)那么函数f(x)就叫做周期函数,非零常数T叫做这个函数的周期.
(2)如果在周期函数f(x)的所有周期中存在一个最小的正数,那么这个最小正数就叫做f(x)的最小正周期.
(3)正弦函数y=sinx(x∈R)和余弦函数y=cosx(x∈R)都是周期函数,最小正周期为,2kπ(且k≠0)是它们的周期.
2.正弦函数、余弦函数的性质
函数
y=sinx
y=cosx
定义域
R
值域
[-1,1]
图象
奇偶性
奇函数
偶函数
周期性
最小正周期:T=2π
单调性
在(k∈Z)上递增;
在(k∈Z)上递减
在(k∈Z)上递增;
在(k∈Z)上递减
最值
当x=时,ymin=-1;
当x=时,ymax=1
当x=时,ymin=-1;
当x=时,ymax=1
对称轴
x=+kπ,k∈Z
x=kπ,k∈Z
对称
中心
(kπ,0),k∈Z
(+kπ,0),k∈Z
五、正切函数的性质
定义域
值域
奇偶性
奇函数
单调性
在上单调递增
例题讲解:
【例1】
求值:(1);
(2);
(3).
【解析】(1);
(2);
(3)
【例2】
化简.
【解】原式
.
【例3】
图中的曲线对应的函数解析式是(
)
A.
B.
C.
D.
【答案】D
【例4】
在上使成立的的取值范围是(
)
A.
B.
C.
D.
【答案】A
【解析】
【分析】由,可得,利用正弦函数的性质得的范围,又因为,再赋值求出即可.
【详解】
,
,
,
又因为,所以当时,,
当时,,
综上:
【例5】
下列函数中,周期为的是(
)
A.
y=sin
B.
y=sin2x
C.
y=cos
D.
y=cos(-4x)
【答案】D
【解析】
【分析】
根据周期公式求解即可.
【详解】根据公式
的周期为,故A错误;
的周期为,故B错误;
的周期为,故C错误;
的周期为,故D正确;
【例6】
函数的最大值是(
)
A.
B.
C.
D.
【答案】C
【解析】
【分析】结合同角三角函数的基本关系式、二次函数的性质,求得函数的最大值.
【详解】
,
当时等号成立,
所以函数的最大值是.
故选:C
课堂运用
1._______.
【答案】
【解析】
2.已知,求的值.
【解】原式
.
3.
函数,,则的范围是(
)
A.
B.
C.
D.
【答案】C
【解析】
【分析】根据正弦函数的单调性直接求解即可.
【详解】根据正弦函数图象可知在区间上,函数先增后减,
当时,,当时,.
故选:C.
4.
函数的简图是(
)
A.
B.
C.
D.
【答案】D
【解析】
【分析】
利用余弦函数的图象平移可得.
【详解】把的图象向上平移1个单位即可.
故选:D
5.
函数的最小正周期是(
)
A.
B.
C.
D.
4
【答案】B
【解析】
【分析】
直接利用周期公式求解即可
【详解】,由周期公式.
6.
函数f(x)=在[—π,π]的图像大致为
A.
B.
C.
D.
【答案】D
【解析】
【分析】先判断函数的奇偶性,得是奇函数,排除A,再注意到选项的区别,利用特殊值得正确答案.
【详解】由,得是奇函数,其图象关于原点对称.又.故选D.
7.
设函数在的图像大致如下图,则f(x)的最小正周期为(
)
A.
B.
C.
D.
【答案】C
【解析】
【分析】由图可得:函数图象过点,即可得到,结合是函数图象与轴负半轴的第一个交点即可得到,即可求得,再利用三角函数周期公式即可得解.
【详解】由图可得:函数图象过点,
将它代入函数可得:
又是函数图象与轴负半轴的第一个交点,
所以,解得:
所以函数的最小正周期为
故选:C
8.
已知向量.
(1)若,求x的值;
(2)记,求函数y=f(x)的最大值和最小值及对应的x的值.
【答案】(1)(2)时,取到最大值3;
时,取到最小值.
【解析】
【分析】(1)根据,利用向量平行的充要条件建立等式,即可求x的值.
(2)根据求解求函数y=f(x)解析式,化简,结合三角函数的性质即可求解最大值和最小值及对应的x的值.
【详解】解:(1)∵向量.
由,
可得:,
即,
∵x∈[0,π]
∴.
(2)由
∵x∈[0,π],
∴
∴当时,即x=0时f(x)max=3;
当,即时.
课后作业:
1.已知函数.
(I)求f(x)的最小正周期;
(II)求证:当时,.
【答案】(1)(2)见解析
【解析】
【详解】试题分析:(Ⅰ)首先根据两角差的余弦公式化简,再根据辅助角公式化简为,最后根据公式求周期;(Ⅱ)先求的范围再求函数的最小值.
试题解析:(Ⅰ).
所以的最小正周期.
(Ⅱ)因为,
所以.
所以.
所以当时,.
2
同课章节目录
