4.2一元二次不等式及其解法(第二课时)课件(共27张PPT)——2021-2022学年高一上学期数学北师大版(2019)必修第一册
文档属性
| 名称 | 4.2一元二次不等式及其解法(第二课时)课件(共27张PPT)——2021-2022学年高一上学期数学北师大版(2019)必修第一册 |  | |
| 格式 | pptx | ||
| 文件大小 | 7.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-26 14:40:25 | ||
图片预览








文档简介
4.2一元二次不等式及其解法
第二课时
制作老师:胡琪
教学目标
01
02
利用三个二次间的关系求参
含参一元二次不等式解法
含参一元二次不等式的解法
重点
难点
三个二次之间的联系
环节一
复习一元二次不等式解法
概括
利用一元二次函数图象解一元二次不等式的步骤
如果有两个不等的根,可以不画图像,直接背口诀:大于两边,小于中间
如果????≤????,没有口诀,看图
?
环节二
含参一元二次不等式解法
角度一
[定序]
两根的大小不确定时,要分类讨论
例1.解关于x的不等式(x-a)(x-a2)<0.
分析
????=???????????????????????图像开口向上,二次项系数不需要讨论;二次方程??????????????????2=0两根是????????=????,????????=????????,是否有根,不需讨论;这两个根的大小是不确定的,需要围绕着????=????,????=????分类讨论。
?
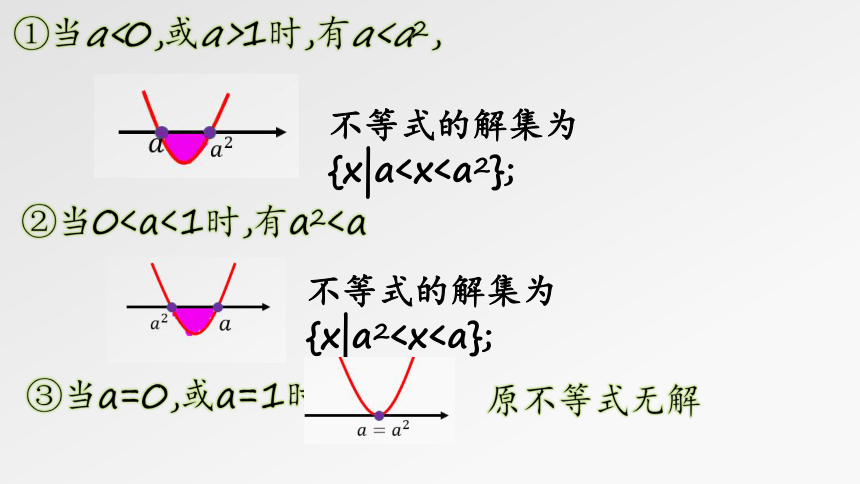
①当a<0,或a>1时,有a不等式的解集为{x|a②当0不等式的解集为{x|a2③当a=0,或a=1时,
原不等式无解
综上,当a<0,或a>1时,原不等式的解集为{x|a当0当a=0,或a=1时,原不等式的解集为?.
小结
角度二
[定根]
有的一元二次不等式对应的方程可以因式分解,有的不能因式分解,我们就用判别式判断是否有根。
例2.解关于x的不等式????????+????????+????>0.
?
分析
二次项系数大于0,这个环节不需要讨论;有没有根?由????=?????????????????,可正可负可零,得讨论; 至于有两个实根????????=?????+????????+????????,????????=???????????????????????????,
大小是确定的,不需要讨论。
?
①当????∈?????,????时,????②当????=±????时,????=????,解集是????????≠????????;
?
??③当????>????或????解集是????????>?????+?????????????????????或?????
角度三
[定型]
二次项的系数若含有参数,要分系数等于0、小于0、大于0讨论,然后将不等式的二次项系数化为正数.
。
例3.解关于x的不等式?????????????????????????+????>????.
?
分析
二次项系数含参,分不清是二次还是一次,所以需要分类定型。
①????=????,原不等式解集为?;
?
②????>????,原不等式可化为:?????????????????+????>????,解集是????????>????,或?????
③?????
综上所述(略写)
角度三
[定型]
二次项的系数若含有参数,要分系数等于0、小于0、大于0讨论,然后将不等式的二次项系数化为正数.
例4.解关于x的不等式ax2+(a-2)x-2≥0(a≥0).
分析
二次项系数含参,分不清是二次还是一次,所以需要分类定型。注意到 a≥0,不必讨论?????
解:当a=0时,原不等式化为x+1≤0,解得x≤-1;
当a>0时,原不等式化为(ax-2)(x+1)≥0,解得x≥????????或x≤-1.
综上所述,a=0时,不等式的解集为{x|x≤-1},
a>0时,不等式的解集为????????≥????????或????≤?????.
?
(1)二次项的系数若含有参数,要分系数等于0、小于0、大于0讨论,然后将不等式的二次项系数化为正数.
(2)若判别式不确定,则需讨论判别式与0的关系.
(3)确定方程无实根时,可直接写出解集,确定方程有两个实数根时,要讨论两个实数根的大小关系,从而写出解集.
含参一元二次(型)不等式解法策略
定型
定根
定序
角度四
[综合]
包含两层或三层分类因素:①【定型】+【定根】;②【定型】+【定序】;③【定根】+【定序】;④【定型】+【定根】+【定序】
例5.解关于x的不等式????+?????????????????????+????≤????.
?
分析
【定型】????>?????、????=?????、????【定根】????=?????????????,????>????,????????.
【综合】①????????
?
简解:当????当????=?????时,不等式的解集是????????≥????????;
当?????当????=????时,不等式的解集是????????=????????;
当????>????时,不等式的解集是?;
?
综合分类时,要做到不重不漏。在讨论过程中,要分清每一个大前提对后续步骤的影响。
含参一元二次(型)不等式解法策略
定型
定根
定序
+
+
环节三
利用三个二次关系求参
例6.若不等式ax2+bx+c≥0的解集是{x?????????≤????≤????},求不等式cx2+bx+a<0的解集.
?
求参
分析
根据三个“二次”之间的关系,-????????和2一定是方程ax2+bx+c=0的两个实数根,所以可以利用根与系数的关系入手解
?
解
由ax2+bx+c≥0的解集为{x?????????≤x≤2},
知-????????,2为方程ax2+bx+c=0的两个实数根,且a<0,
所以-????????=-????????+2=????????,????????=?????????×2=-????????,
?
即????????=-????????,????????=-????????,
所以b=-????????a,c=-????????a,
所以不等式cx2+bx+a<0变为?????????????x2+?????????????x+a<0,
即2ax2+5ax-3a>0.(*)
又因为a<0,所以(*)式可化为2x2+5x-3<0,
解得-3 故所求不等式的解集为{x??????
练习
已知一元二次不等式ax2+bx+1≤0的解集为
{x?????????≤????≤?????????},求不等式x2-bx+a>0的解集
?
因为不等式ax2+bx+1≤0的解集是{x?????????≤????≤?????????},
所以方程ax2+bx+1=0有两个不相等的实数根x1=-????????,x2=-????????;
于是有?????????=????????+????????=?????????,????????=????????????????=????????,解得a=6,b=5,
所以不等式x2-bx+a>0可化为x2-5x+6>0,
即(x-2)(x-3)>0,解得x>3或x<2.
故所求不等式的解集为{x|x<2,或x>3}.
?
核对答案
环节四
小结
课堂小结
1.核心要点
含参一元二次不等式解法题型归类
2.数学素养
体会数形结合思想、分类讨论思想的应用,加强运算能力素养的培养.
由一元二次不等式解集求参
谢谢观看
课件制作老师:胡琪
第二课时
制作老师:胡琪
教学目标
01
02
利用三个二次间的关系求参
含参一元二次不等式解法
含参一元二次不等式的解法
重点
难点
三个二次之间的联系
环节一
复习一元二次不等式解法
概括
利用一元二次函数图象解一元二次不等式的步骤
如果有两个不等的根,可以不画图像,直接背口诀:大于两边,小于中间
如果????≤????,没有口诀,看图
?
环节二
含参一元二次不等式解法
角度一
[定序]
两根的大小不确定时,要分类讨论
例1.解关于x的不等式(x-a)(x-a2)<0.
分析
????=???????????????????????图像开口向上,二次项系数不需要讨论;二次方程??????????????????2=0两根是????????=????,????????=????????,是否有根,不需讨论;这两个根的大小是不确定的,需要围绕着????=????,????=????分类讨论。
?
①当a<0,或a>1时,有a
原不等式无解
综上,当a<0,或a>1时,原不等式的解集为{x|a
小结
角度二
[定根]
有的一元二次不等式对应的方程可以因式分解,有的不能因式分解,我们就用判别式判断是否有根。
例2.解关于x的不等式????????+????????+????>0.
?
分析
二次项系数大于0,这个环节不需要讨论;有没有根?由????=?????????????????,可正可负可零,得讨论; 至于有两个实根????????=?????+????????+????????,????????=???????????????????????????,
大小是确定的,不需要讨论。
?
①当????∈?????,????时,????②当????=±????时,????=????,解集是????????≠????????;
?
??③当????>????或????解集是????????>?????+?????????????????????或?????
角度三
[定型]
二次项的系数若含有参数,要分系数等于0、小于0、大于0讨论,然后将不等式的二次项系数化为正数.
。
例3.解关于x的不等式?????????????????????????+????>????.
?
分析
二次项系数含参,分不清是二次还是一次,所以需要分类定型。
①????=????,原不等式解集为?;
?
②????>????,原不等式可化为:?????????????????+????>????,解集是????????>????,或?????
③?????
综上所述(略写)
角度三
[定型]
二次项的系数若含有参数,要分系数等于0、小于0、大于0讨论,然后将不等式的二次项系数化为正数.
例4.解关于x的不等式ax2+(a-2)x-2≥0(a≥0).
分析
二次项系数含参,分不清是二次还是一次,所以需要分类定型。注意到 a≥0,不必讨论?????
解:当a=0时,原不等式化为x+1≤0,解得x≤-1;
当a>0时,原不等式化为(ax-2)(x+1)≥0,解得x≥????????或x≤-1.
综上所述,a=0时,不等式的解集为{x|x≤-1},
a>0时,不等式的解集为????????≥????????或????≤?????.
?
(1)二次项的系数若含有参数,要分系数等于0、小于0、大于0讨论,然后将不等式的二次项系数化为正数.
(2)若判别式不确定,则需讨论判别式与0的关系.
(3)确定方程无实根时,可直接写出解集,确定方程有两个实数根时,要讨论两个实数根的大小关系,从而写出解集.
含参一元二次(型)不等式解法策略
定型
定根
定序
角度四
[综合]
包含两层或三层分类因素:①【定型】+【定根】;②【定型】+【定序】;③【定根】+【定序】;④【定型】+【定根】+【定序】
例5.解关于x的不等式????+?????????????????????+????≤????.
?
分析
【定型】????>?????、????=?????、????【定根】????=?????????????,????>????,????????.
【综合】①????????
?
简解:当????当????=?????时,不等式的解集是????????≥????????;
当?????当????=????时,不等式的解集是????????=????????;
当????>????时,不等式的解集是?;
?
综合分类时,要做到不重不漏。在讨论过程中,要分清每一个大前提对后续步骤的影响。
含参一元二次(型)不等式解法策略
定型
定根
定序
+
+
环节三
利用三个二次关系求参
例6.若不等式ax2+bx+c≥0的解集是{x?????????≤????≤????},求不等式cx2+bx+a<0的解集.
?
求参
分析
根据三个“二次”之间的关系,-????????和2一定是方程ax2+bx+c=0的两个实数根,所以可以利用根与系数的关系入手解
?
解
由ax2+bx+c≥0的解集为{x?????????≤x≤2},
知-????????,2为方程ax2+bx+c=0的两个实数根,且a<0,
所以-????????=-????????+2=????????,????????=?????????×2=-????????,
?
即????????=-????????,????????=-????????,
所以b=-????????a,c=-????????a,
所以不等式cx2+bx+a<0变为?????????????x2+?????????????x+a<0,
即2ax2+5ax-3a>0.(*)
又因为a<0,所以(*)式可化为2x2+5x-3<0,
解得-3
练习
已知一元二次不等式ax2+bx+1≤0的解集为
{x?????????≤????≤?????????},求不等式x2-bx+a>0的解集
?
因为不等式ax2+bx+1≤0的解集是{x?????????≤????≤?????????},
所以方程ax2+bx+1=0有两个不相等的实数根x1=-????????,x2=-????????;
于是有?????????=????????+????????=?????????,????????=????????????????=????????,解得a=6,b=5,
所以不等式x2-bx+a>0可化为x2-5x+6>0,
即(x-2)(x-3)>0,解得x>3或x<2.
故所求不等式的解集为{x|x<2,或x>3}.
?
核对答案
环节四
小结
课堂小结
1.核心要点
含参一元二次不等式解法题型归类
2.数学素养
体会数形结合思想、分类讨论思想的应用,加强运算能力素养的培养.
由一元二次不等式解集求参
谢谢观看
课件制作老师:胡琪
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
