北师大版八年级数学上册1.1探索勾股定理一课一练习题2(Word版,含答案)
文档属性
| 名称 | 北师大版八年级数学上册1.1探索勾股定理一课一练习题2(Word版,含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 359.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-02 16:30:50 | ||
图片预览



文档简介
1.1《探索勾股定理》习题2
一、选择题
1.如图,在边长为1个单位长度的小正方形组成的网格中,点A、B都是格点,则线段AB的长度为( )
A.5
B.6
C.7
D.25
2.如图,已知点E在正方形ABCD内,满足∠AEB=90°,AE=6,BE=8,则阴影部分的面积是( )
A.48
B.60
C.76
D.80
3.如图,在
Rt△ABC
中,AC=3,BC=5,阴影部分是以
AB
为边的一个正方形,
则此正方形的面积为(
)
A.4
B.15
C.16
D.34
4.在Rt△ABC中,∠C=90°,a=8,c=17,则b的长是( )
A.25
B.18
C.15
D.13
5.在平面直角坐标系中,,,其中,则下列对长度判断正确的是(
)
A.
B.
C.
D.无法确定
6.如图,长为8cm的橡皮筋放置在x轴上,固定两端A和B,然后把中点C向上拉升3cm至D点,则橡皮筋被拉长了(
)
A.2cm
B.3cm
C.4cm
D.5cm
7.如图:图形A的面积是(??
??
)
A.225
B.144
C.81
D.无法确定
8.现在人们锻炼身体的意识日渐増强,但是一些人保护环境的意识却很淡薄,如图是兴庆公园的一角,有人为了抄近道而避开横平竖直的路的拐角∠ABC,而走“捷径AC’于是在草坪内走出了一条不该有的“路AC”,已知AB=40米,BC=30米,他们踩坏了___米的草坪,只为少走___米路( )
A.20、50
B.50、20
C.20、30
D.30、20
9.若直角三角形中,斜边的长为13,一条直角边长为5,则这个三角形的面积是(
)
A.60
B.30
C.20
D.32
10.如图,以Rt△ABC的三边为边长向外作正方形,三个正方形的面积分别为、、,若,,则的值为(
)
A.1
B.5
C.25
D.144
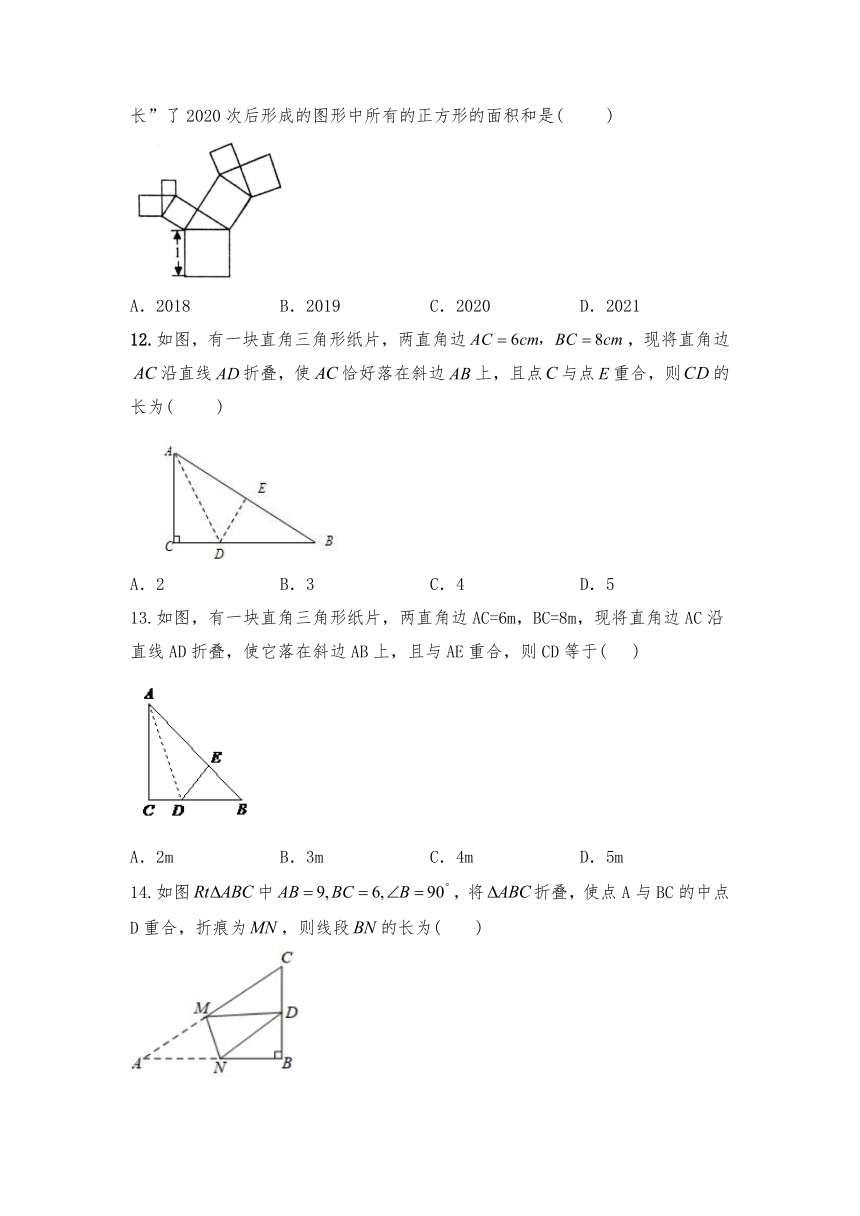
11.有一个面积为1的正方形,经过一次“生长”后,在他的左右肩上生出两个小正方形,其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,变成了下图,如果继续“生长”下去,它将变得“枝繁叶茂”,请你算出“生长”了2020次后形成的图形中所有的正方形的面积和是(
)
A.2018
B.2019
C.2020
D.2021
12.如图,有一块直角三角形纸片,两直角边,现将直角边沿直线折叠,使恰好落在斜边上,且点与点重合,则的长为(
)
A.2
B.3
C.4
D.5
13.如图,有一块直角三角形纸片,两直角边AC=6m,BC=8m,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于(
)
A.2m
B.3m
C.4m
D.5m
14.如图中,将折叠,使点A与BC的中点D重合,折痕为,则线段的长为(
)
A.4
B.
C.5
D.6
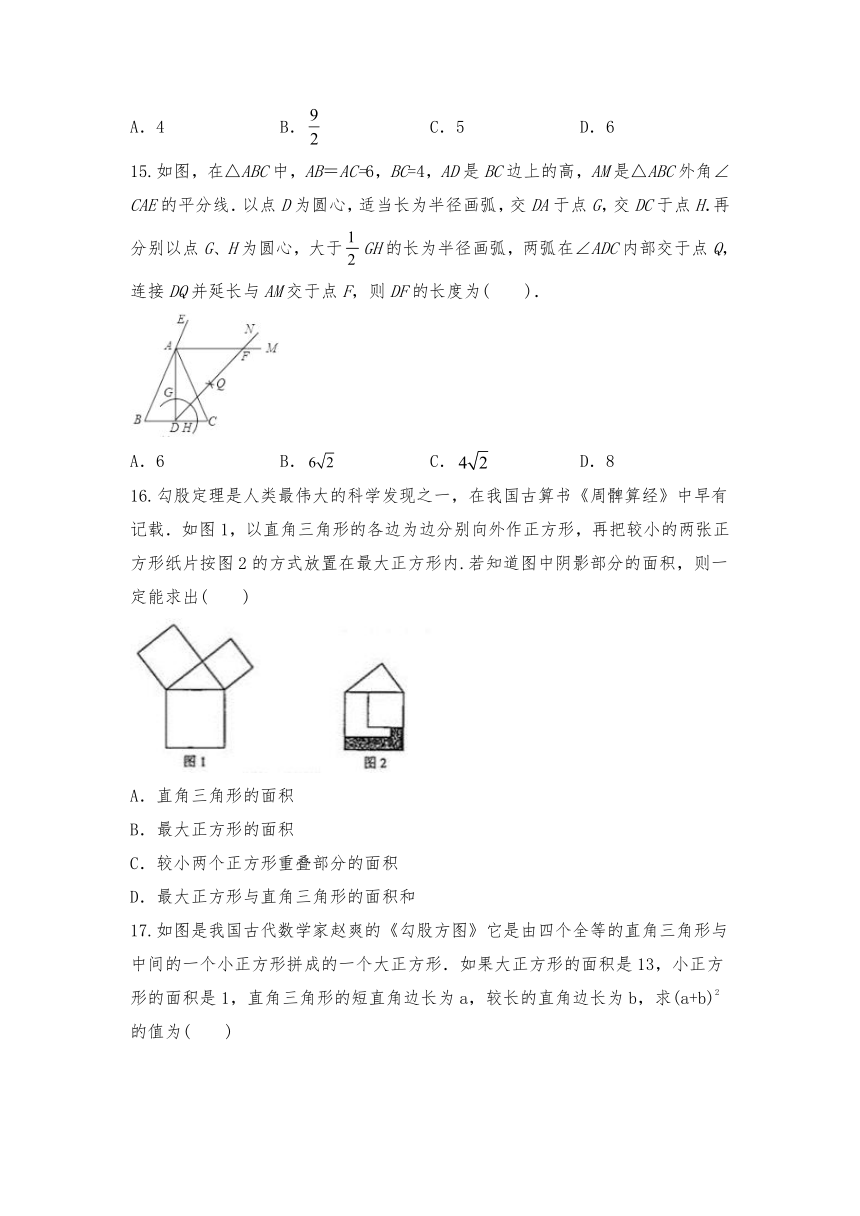
15.如图,在△ABC中,AB=AC=6,BC=4,AD是BC边上的高,AM是△ABC外角∠CAE的平分线.以点D为圆心,适当长为半径画弧,交DA于点G,交DC于点H.再分别以点G、H为圆心,大于GH的长为半径画弧,两弧在∠ADC内部交于点Q,连接DQ并延长与AM交于点F,则DF的长度为(
).
A.6
B.
C.
D.8
16.勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出(
)
A.直角三角形的面积
B.最大正方形的面积
C.较小两个正方形重叠部分的面积
D.最大正方形与直角三角形的面积和
17.如图是我国古代数学家赵爽的《勾股方图》它是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形.如果大正方形的面积是13,小正方形的面积是1,直角三角形的短直角边长为a,较长的直角边长为b,求(a+b)2的值为(
)
A.169
B.25
C.19
D.13
18.在△ABC中,AB=AC=5,P是BC上异于B,C的一点,则AP2+BP?PC的值是( )
A.15
B.25
C.30
D.20
19.如图是一张直角三角形的纸片,两直角边AC=6
cm、BC=8
cm,现将△ABC折叠,使点B与点A重合,折痕为DE,则BE的长为(
)
A.4
cm
B.5
cm
C.6
cm
D.10
cm
二、解答题
1.如图,在中,,,,将折叠,使点恰好落在边上,与点重合,为折痕,则多少?
2.如图,已知在Rt△ABC中,∠ACB=90°,AB=10,分别以AC,BC为直径作半圆,面积分别记为S1,S2,则S1+S2等于多少
3.在直角三角形ABC中,斜边AB=1,则AB2+BC2+AC2的值是多少
4.如图,在矩形ABCD中,AB=8,BC=10,E为CD边上一点,将△ADE沿AE折叠,使点D落在BC边上的点F处.
(1)求BF的长;
(2)求CE的长.
5.已知在中,是的中点,,垂足为,交于点,且.
(1)求的度数;
(2)若,,求的长.
6.小王剪了两张直角三角形纸片,进行了如下的操作:
操作一:如图1,将Rt△ABC沿某条直线折叠,使斜边的两个端点A与B重合,折痕为DE.
(1)如果AC=6cm,BC=8cm,可求得△ACD的周长为______;
(2)如果∠CAD:∠BAD=4:7,可求得∠B的度数为______;
操作二:如图2,小王拿出另一张Rt△ABC纸片,将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,若AC=9cm,BC=12cm,请求出CD的长.
7.如图,,,于点.求证:
.
8.如图,在⊿中,,于,
.
⑴.求的长;
⑵.求
的长.
9.如图,在四边形中,,,.求证:.
答案
一、选择题
1.A
2.C
3.D.
4.C.
5.C.6.A
7.C.
8.B.
9.B.
10.A
11.D
12.B
13.B
14.A.
15.D
16.C.
17.B
18.B
19.B
二、解答题
1.解:根据折叠的性质可得BE=EB′,AB′=AB=30,
设BE=EB′=x,则EC=40﹣x,
∵∠B=90°,AB=30,BC=40,
∴在Rt△ABC中,由勾股定理得,AC=50,
∴B′C=50﹣30=20,
在Rt△B′EC中,由勾股定理得,x2+202=(40﹣x)2,
解得x=15.
2.在Rt△ABC中,∠ACB=90°,
则由勾股定理知,.
,,
∴
3.解:如右图所示,
在Rt△ABC中,AB2=BC2+AC2,
又∵AB=1,
∴BC2+AC2,=AB2=1,
∴AB2+BC2+AC2=1+1=2.
4.解:(1)∵四边形ABCD为矩形,
∴∠B=90°,且AD=BC=10,
又∵AFE是由ADE沿AE翻折得到的,
∴AF=AD=10,
又∵AB=8,
在ABF中,由勾股定理得:,
故BF的长为6.
(2)设CE=x
,
∵四边形ABCD为矩形,
∴CD=AB=8,∠C=90°,DE=CD-CE=8-x,
又∵△AFE是由△ADE沿AE翻折得到的,
∴FE=DE=8-x,
由(1)知:BF=6,故CF=BC-BF=10-6=4,
在CEF中,由勾股定理得:,
∴,解得:x=3,
故CE的长为3.
5.(1)连接CE,∵D是BC的中点,DE⊥BC,
∴CE=BE.
∵BE2?AE2=AC2,
∴AE2+AC2=CE2.
∴△AEC是直角三角形,∠A=90°;
(2)在Rt△BDE中,BE==5.
所以CE=BE=5.
设AE=x,则在Rt△AEC中,AC2=CE2?AE2,
所以AC2=25?x2.
∵BD=4,
∴BC=2BD=8.
在Rt△ABC中,根据BC2=AB2+AC2,
即64=(5+x)2+25?x2,
解得x=1.4.
即AE=1.4.
6.(1)由折叠的性质可得AD=BD,∵△ACD的周长=AC+CD+AD,
∴△ACD的周长=AC+CD+BD=AC+BC=8+6=14(cm);
(2)设∠CAD=4x,∠BAD=7x由题意得方程:
7x+7x+4x=90,
解之得x=5,
所以∠B=35°;
操作二:∵AC=9cm,BC=12cm,
∴AB=(cm),
根据折叠性质可得AC=AE=9cm,
∴BE=AB-AE=6cm,
设CD=x,则BD=12-x,DE=x,
在Rt△BDE中,由题意可得方程x2+62=(12-x)2,
解之得x=4.5,
7.证明:∵
,
∴在Rt△BCM中,,
∵
∴,
∴在Rt△APM中,,即,
∵在Rt△MPB中,
∴
∵,
∴,
∴.
8.解:(1).∵在⊿中,,.
∴,
(2).∵⊿,
∴即,
∴20×15=25CD.
∴.
9.证明:在△ABC中,∠ABC=90°,
∴.
在△ACD中,CD⊥AD,
∴,
∴.
又AD2=2AB2-CD2,
∴,
即,
∴.
一、选择题
1.如图,在边长为1个单位长度的小正方形组成的网格中,点A、B都是格点,则线段AB的长度为( )
A.5
B.6
C.7
D.25
2.如图,已知点E在正方形ABCD内,满足∠AEB=90°,AE=6,BE=8,则阴影部分的面积是( )
A.48
B.60
C.76
D.80
3.如图,在
Rt△ABC
中,AC=3,BC=5,阴影部分是以
AB
为边的一个正方形,
则此正方形的面积为(
)
A.4
B.15
C.16
D.34
4.在Rt△ABC中,∠C=90°,a=8,c=17,则b的长是( )
A.25
B.18
C.15
D.13
5.在平面直角坐标系中,,,其中,则下列对长度判断正确的是(
)
A.
B.
C.
D.无法确定
6.如图,长为8cm的橡皮筋放置在x轴上,固定两端A和B,然后把中点C向上拉升3cm至D点,则橡皮筋被拉长了(
)
A.2cm
B.3cm
C.4cm
D.5cm
7.如图:图形A的面积是(??
??
)
A.225
B.144
C.81
D.无法确定
8.现在人们锻炼身体的意识日渐増强,但是一些人保护环境的意识却很淡薄,如图是兴庆公园的一角,有人为了抄近道而避开横平竖直的路的拐角∠ABC,而走“捷径AC’于是在草坪内走出了一条不该有的“路AC”,已知AB=40米,BC=30米,他们踩坏了___米的草坪,只为少走___米路( )
A.20、50
B.50、20
C.20、30
D.30、20
9.若直角三角形中,斜边的长为13,一条直角边长为5,则这个三角形的面积是(
)
A.60
B.30
C.20
D.32
10.如图,以Rt△ABC的三边为边长向外作正方形,三个正方形的面积分别为、、,若,,则的值为(
)
A.1
B.5
C.25
D.144
11.有一个面积为1的正方形,经过一次“生长”后,在他的左右肩上生出两个小正方形,其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,变成了下图,如果继续“生长”下去,它将变得“枝繁叶茂”,请你算出“生长”了2020次后形成的图形中所有的正方形的面积和是(
)
A.2018
B.2019
C.2020
D.2021
12.如图,有一块直角三角形纸片,两直角边,现将直角边沿直线折叠,使恰好落在斜边上,且点与点重合,则的长为(
)
A.2
B.3
C.4
D.5
13.如图,有一块直角三角形纸片,两直角边AC=6m,BC=8m,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于(
)
A.2m
B.3m
C.4m
D.5m
14.如图中,将折叠,使点A与BC的中点D重合,折痕为,则线段的长为(
)
A.4
B.
C.5
D.6
15.如图,在△ABC中,AB=AC=6,BC=4,AD是BC边上的高,AM是△ABC外角∠CAE的平分线.以点D为圆心,适当长为半径画弧,交DA于点G,交DC于点H.再分别以点G、H为圆心,大于GH的长为半径画弧,两弧在∠ADC内部交于点Q,连接DQ并延长与AM交于点F,则DF的长度为(
).
A.6
B.
C.
D.8
16.勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出(
)
A.直角三角形的面积
B.最大正方形的面积
C.较小两个正方形重叠部分的面积
D.最大正方形与直角三角形的面积和
17.如图是我国古代数学家赵爽的《勾股方图》它是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形.如果大正方形的面积是13,小正方形的面积是1,直角三角形的短直角边长为a,较长的直角边长为b,求(a+b)2的值为(
)
A.169
B.25
C.19
D.13
18.在△ABC中,AB=AC=5,P是BC上异于B,C的一点,则AP2+BP?PC的值是( )
A.15
B.25
C.30
D.20
19.如图是一张直角三角形的纸片,两直角边AC=6
cm、BC=8
cm,现将△ABC折叠,使点B与点A重合,折痕为DE,则BE的长为(
)
A.4
cm
B.5
cm
C.6
cm
D.10
cm
二、解答题
1.如图,在中,,,,将折叠,使点恰好落在边上,与点重合,为折痕,则多少?
2.如图,已知在Rt△ABC中,∠ACB=90°,AB=10,分别以AC,BC为直径作半圆,面积分别记为S1,S2,则S1+S2等于多少
3.在直角三角形ABC中,斜边AB=1,则AB2+BC2+AC2的值是多少
4.如图,在矩形ABCD中,AB=8,BC=10,E为CD边上一点,将△ADE沿AE折叠,使点D落在BC边上的点F处.
(1)求BF的长;
(2)求CE的长.
5.已知在中,是的中点,,垂足为,交于点,且.
(1)求的度数;
(2)若,,求的长.
6.小王剪了两张直角三角形纸片,进行了如下的操作:
操作一:如图1,将Rt△ABC沿某条直线折叠,使斜边的两个端点A与B重合,折痕为DE.
(1)如果AC=6cm,BC=8cm,可求得△ACD的周长为______;
(2)如果∠CAD:∠BAD=4:7,可求得∠B的度数为______;
操作二:如图2,小王拿出另一张Rt△ABC纸片,将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,若AC=9cm,BC=12cm,请求出CD的长.
7.如图,,,于点.求证:
.
8.如图,在⊿中,,于,
.
⑴.求的长;
⑵.求
的长.
9.如图,在四边形中,,,.求证:.
答案
一、选择题
1.A
2.C
3.D.
4.C.
5.C.6.A
7.C.
8.B.
9.B.
10.A
11.D
12.B
13.B
14.A.
15.D
16.C.
17.B
18.B
19.B
二、解答题
1.解:根据折叠的性质可得BE=EB′,AB′=AB=30,
设BE=EB′=x,则EC=40﹣x,
∵∠B=90°,AB=30,BC=40,
∴在Rt△ABC中,由勾股定理得,AC=50,
∴B′C=50﹣30=20,
在Rt△B′EC中,由勾股定理得,x2+202=(40﹣x)2,
解得x=15.
2.在Rt△ABC中,∠ACB=90°,
则由勾股定理知,.
,,
∴
3.解:如右图所示,
在Rt△ABC中,AB2=BC2+AC2,
又∵AB=1,
∴BC2+AC2,=AB2=1,
∴AB2+BC2+AC2=1+1=2.
4.解:(1)∵四边形ABCD为矩形,
∴∠B=90°,且AD=BC=10,
又∵AFE是由ADE沿AE翻折得到的,
∴AF=AD=10,
又∵AB=8,
在ABF中,由勾股定理得:,
故BF的长为6.
(2)设CE=x
,
∵四边形ABCD为矩形,
∴CD=AB=8,∠C=90°,DE=CD-CE=8-x,
又∵△AFE是由△ADE沿AE翻折得到的,
∴FE=DE=8-x,
由(1)知:BF=6,故CF=BC-BF=10-6=4,
在CEF中,由勾股定理得:,
∴,解得:x=3,
故CE的长为3.
5.(1)连接CE,∵D是BC的中点,DE⊥BC,
∴CE=BE.
∵BE2?AE2=AC2,
∴AE2+AC2=CE2.
∴△AEC是直角三角形,∠A=90°;
(2)在Rt△BDE中,BE==5.
所以CE=BE=5.
设AE=x,则在Rt△AEC中,AC2=CE2?AE2,
所以AC2=25?x2.
∵BD=4,
∴BC=2BD=8.
在Rt△ABC中,根据BC2=AB2+AC2,
即64=(5+x)2+25?x2,
解得x=1.4.
即AE=1.4.
6.(1)由折叠的性质可得AD=BD,∵△ACD的周长=AC+CD+AD,
∴△ACD的周长=AC+CD+BD=AC+BC=8+6=14(cm);
(2)设∠CAD=4x,∠BAD=7x由题意得方程:
7x+7x+4x=90,
解之得x=5,
所以∠B=35°;
操作二:∵AC=9cm,BC=12cm,
∴AB=(cm),
根据折叠性质可得AC=AE=9cm,
∴BE=AB-AE=6cm,
设CD=x,则BD=12-x,DE=x,
在Rt△BDE中,由题意可得方程x2+62=(12-x)2,
解之得x=4.5,
7.证明:∵
,
∴在Rt△BCM中,,
∵
∴,
∴在Rt△APM中,,即,
∵在Rt△MPB中,
∴
∵,
∴,
∴.
8.解:(1).∵在⊿中,,.
∴,
(2).∵⊿,
∴即,
∴20×15=25CD.
∴.
9.证明:在△ABC中,∠ABC=90°,
∴.
在△ACD中,CD⊥AD,
∴,
∴.
又AD2=2AB2-CD2,
∴,
即,
∴.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
