广东省实验中学2011-2012学年高一下学期模块考试题数学
文档属性
| 名称 | 广东省实验中学2011-2012学年高一下学期模块考试题数学 |  | |
| 格式 | zip | ||
| 文件大小 | 202.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-26 16:35:15 | ||
图片预览




文档简介
广东实验中学2011—2012学年(下)高一级模块考试
数 学
本试卷分基础检测与能力检测两部分,共4页.满分为150分。考试用时120分钟.
注意事项:
1.答卷前,考生务必用黑色字迹钢笔或签字笔将自己的姓名和考生号填写在答卷上,并用2B铅笔填涂学号.
2.选择题每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其它答案标号,不能答在试题卷上.
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内的相应位置上;如需改动,先划掉原来的答案,然后写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.
第一部分 基础检测(共100分)
一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知为等比数列,,则=( )
A.16 B. C.4 D.
2.在中,,,,则的值为( )
A. B. C. 或 D. 不存在
3.已知向量,,其中,函数的最大值为( )
A. B. C. D.
4.设等差数列的前项和为,若,,则( )
A.63 B.45 C.36 D.27
5.在中,a、b、c分别是角A、B、C的对边,若,则的形状是( )
A.等腰三角形 B.等边三角形 C.直角三角形 D.锐角三角形
6.已知,,则的值为( )
A. B. C. D.
7.数列的前项和为,则( )
A. B.30 C.28 D.14
8.的值是( )
A. B. C.1 D.
9.在数列中,,,则=( )
A. B. C. D.
10.对于非零向量,下列运算中正确的有( )个.
① ②
③ ④
A.3个 B.2个 C.1个 D.0个
二、填空题:本大题共4小题,每小题5分,共20分.
11.已知数列为等差数列,且,,则_____________.
11.已知,则=.
13.在中,a、b、c分别是角A、B、C的对边. 若,,则的外接圆半径等于_____________.
14.等差数列与等比数列之间是存在某种结构的类比关系的,例如从定义看,或者从通项公式看,都可以发现这种类比的原则. 按照此思想,请把下面等差数列的性质,类比到等比数列,写出相应的性质:
若为等差数列,,则公差;若是各项均为正数的等比数列,,则公比_________________.
三、解答题:本大题共3小题,共30分.解答应写出文字说明、证明过程或演算步骤.
15.(本题满分9分)设,是两个相互垂直的单位向量,且,
(1)若,求的值;
(2)当时,求夹角的余弦值.
16.(本题满分12分)已知等比数列的前项和为,,,
(1)求等比数列的通项公式;
(2)令,证明数列为等差数列;
(3)对(2)中的数列,前项和为,求使最小时的的值.
17.(本题满分9分)已知,.
(1)化简,并求值.
(2)若,且,求及的值.
第二部分 能力检测(共50分)
四、填空题:本大题共2小题,每小题5分,共10分.
18.若数列满足,且,则通项________________.
19.课本介绍过平面向量数量积运算的几何意义:等于的长度与在方向上的投影的乘积. 运用几何意义,有时能得到更巧妙的解题思路. 例如:边长为1的正六边形ABCDEF中,点P是正六边形内的一点(含边界),则的取值范围是_____________.
五、解答题:本大题共3小题,共40分.解答应写出文字说明、证明过程或演算步骤.
20.(本题满分12分)在△ABC中,a、b、c分别是角A、B、C的对边,且.
(1)若,面积,求b+c的值;
(2)求的值(注意,此问只能使用题干的条件,不能用(1)问的条件).
21.(本题满分14分)设数列的前项和为,且.
(1)求数列的通项公式;
(2)若,为数列的前项和. 求;
(3)是否存在自然数,使得对一切恒成立?若存在,求出的值;若不存在,说明理由.
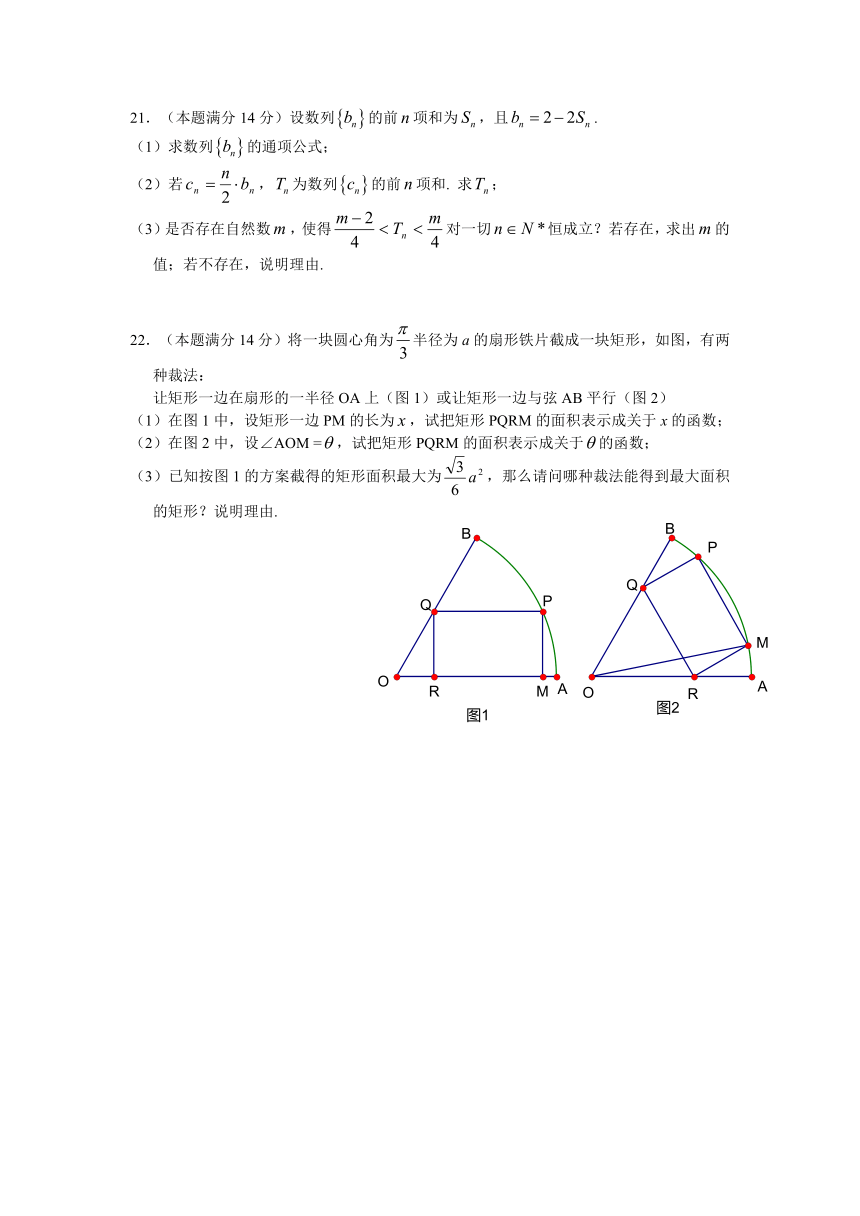
22.(本题满分14分)将一块圆心角为半径为a的扇形铁片截成一块矩形,如图,有两种裁法:
让矩形一边在扇形的一半径OA上(图1)或让矩形一边与弦AB平行(图2)
(1)在图1中,设矩形一边PM的长为,试把矩形PQRM的面积表示成关于x的函数;
(2)在图2中,设∠AOM =,试把矩形PQRM的面积表示成关于的函数;
(3)已知按图1的方案截得的矩形面积最大为,那么请问哪种裁法能得到最大面积的矩形?说明理由.
广东实验中学2011—2012学年高一级模块考试
数学 参考答案
第一部分 基础检测(共100分)
一、选择题:本大题共10小题,每小题5分,共50分
1、已知为等比数列,,则=( A )
A.16 B. C.4 D.
2、在中,,,,则的值为( C )
A. B. C. 或 D. 不存在
3、已知向量,,其中,函数的最大值为( D )
A. B. C. D.
4、设等差数列的前项和为,若,,则( B )
A.63 B.45 C.36 D.27
5、在中,a、b、c分别是角A、B、C的对边,若,则的形状是( A )
A.等腰三角形 B.等边三角形 C.直角三角形 D.锐角三角形
6、已知,,则的值为( C )
A. B. C. D.
7、数列的前项和为,则( D )
A. B.30 C.28 D.14
8、的值是( B )
A. B. C.1 D.
9、在数列中,,,则=( A )
A. B. C. D.
10、对于非零向量,下列运算中正确的有( D )个.
① ②
③ ④
A.3个 B.2个 C.1个 D.0个
二、填空题:本大题共4小题,每小题5分,共20分.
11、已知数列为等差数列,且,,则_____________.
11、已知,则=.
13、在中,a、b、c分别是角A、B、C的对边. 若,,则的外接圆半径等于_____________. 1
14、等差数列与等比数列之间是存在某种结构的类比关系的,例如从定义看,或者从通项公式看,都可以发现这种类比的原则. 按照此思想,请把下面等差数列的性质,类比到等比数列,写出相应的性质:
若为等差数列,,则公差;若是各项均为正数的等比数列,,则公比_________________.
三、解答题:本大题共3小题,共30分.
15、(本题满分9分)设,是两个相互垂直的单位向量,且,
(1)若,求的值;
(2)当时,求夹角的余弦值.
解:(1),,即 ……1分
化简得 ……2分
又,是两个相互垂直的单位向量,, ……3分
,. ……4分
(2)当时,
……5分
, ……7分
……9分
16、(本题满分12分)已知等比数列的前项和为,,,
(1)求等比数列的通项公式;
(2)令,证明数列为等差数列;
(3)对(2)中的数列,前项和为,求使最小时的的值.
解:(1), ,……2分
两式子相除得 , ……3分 代入解得,……4分
. ……5分
(2) ……6分
,为等差数列. ……8分
(3)方法一:令,得, ……10分
解得,……11分 当或时,前项和为最小. ……12分
方法二:, ……10分
对称轴方程为,……11分 当或时,前项和为最小. ……12分
17、(本题满分9分)已知,.
(1)化简,并求值.
(2)若,且,求及的值.
解:(1) ……2分
……3分
(2),, 又,
……5分
由,,得, ……6分
……7分
……9分
第二部分 能力检测(共50分)
四、选择题:本大题共2小题,每小题5分,共10分.
18、若数列满足,且,则通项________________.
19、课本介绍过平面向量数量积运算的几何意义:等于的长度与在方向上的投影的乘积. 运用几何意义,有时能得到更巧妙的解题思路. 例如:边长为1的正六边形ABCDEF中,点P是正六边形内的一点(含边界),则的取值范围是_____________.
五、解答题:本大题共3小题,共40分.解答应写出文字说明、证明过程或演算步骤.
20、(本题满分12分)在△ABC中,a、b、c分别是角A、B、C的对边,且.
(1)若,面积,求b+c的值;
(2)求的值(注意,此问只能使用题干的条件,不能用(1)问的条件).
解:(1),……1分 ……2分
由余弦定理 ……4分
得 ……5分
, ……6分
(2)由正弦定理知 ……8分
……10分
……12分
21、(本题满分14分)设数列的前项和为,且.
(1)求数列的通项公式;
(2)若,为数列的前项和. 求;
(3)是否存在自然数,使得对一切恒成立?若存在,求出的值;若不存在,说明理由.
解:(1)由,令,则,又,所以. ……1分
当时,由, ……2分
可得. 即. ……3分
所以是以为首项,为公比的等比数列,于是. ……4分
(2) ……5分
∴
……6分
∴. ……7分
, ……8分
从而.(写成也可) ……9分
(3),故单调递增
,又, ……11分
要恒成立,则, ……12分
解得,……13分 又,故. ……14分
22、(本题满分14分)将一块圆心角为半径为a的扇形铁片截成一块矩形,如图,有两种裁法:
让矩形一边在扇形的一半径OA上(图1)或让矩形一边与弦AB平行(图2)
(1)在图1中,设矩形一边PM的长为,试把矩形PQRM的面积表示成关于x的函数;
(2)在图2中,设∠AOM =,试把矩形PQRM的面积表示成关于的函数;
(3)已知按图1的方案截得的矩形面积最大为,那么请问哪种裁法能得到最大面积的矩形?说明理由.
解:(1)PM=QR=x,
在RT△QRO中,OR=
在RT△PMO中,OM=
RM=OM-OR=……2分
, ……3分
(2)∠MRA =×=,∠MRO =,
在△OMR中,由正弦定理,得:=,即RM = 2a·sin, ……6分
又=,∴OR = 2a·sin(-), ……8分
又正△ORQ中,QR=OR=2a·sin(-)
∴矩形的MPQR的面积为S= MR·PQ = 4a·sin·sin(-) ……9分
(3)对于(2)中的函数
……11分
当,即时, ……13分
,故按图1的方案能得到最大面积的矩形. ……14分
A
B
C
D
E
F
A
B
C
D
E
F
数 学
本试卷分基础检测与能力检测两部分,共4页.满分为150分。考试用时120分钟.
注意事项:
1.答卷前,考生务必用黑色字迹钢笔或签字笔将自己的姓名和考生号填写在答卷上,并用2B铅笔填涂学号.
2.选择题每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其它答案标号,不能答在试题卷上.
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内的相应位置上;如需改动,先划掉原来的答案,然后写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.
第一部分 基础检测(共100分)
一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知为等比数列,,则=( )
A.16 B. C.4 D.
2.在中,,,,则的值为( )
A. B. C. 或 D. 不存在
3.已知向量,,其中,函数的最大值为( )
A. B. C. D.
4.设等差数列的前项和为,若,,则( )
A.63 B.45 C.36 D.27
5.在中,a、b、c分别是角A、B、C的对边,若,则的形状是( )
A.等腰三角形 B.等边三角形 C.直角三角形 D.锐角三角形
6.已知,,则的值为( )
A. B. C. D.
7.数列的前项和为,则( )
A. B.30 C.28 D.14
8.的值是( )
A. B. C.1 D.
9.在数列中,,,则=( )
A. B. C. D.
10.对于非零向量,下列运算中正确的有( )个.
① ②
③ ④
A.3个 B.2个 C.1个 D.0个
二、填空题:本大题共4小题,每小题5分,共20分.
11.已知数列为等差数列,且,,则_____________.
11.已知,则=.
13.在中,a、b、c分别是角A、B、C的对边. 若,,则的外接圆半径等于_____________.
14.等差数列与等比数列之间是存在某种结构的类比关系的,例如从定义看,或者从通项公式看,都可以发现这种类比的原则. 按照此思想,请把下面等差数列的性质,类比到等比数列,写出相应的性质:
若为等差数列,,则公差;若是各项均为正数的等比数列,,则公比_________________.
三、解答题:本大题共3小题,共30分.解答应写出文字说明、证明过程或演算步骤.
15.(本题满分9分)设,是两个相互垂直的单位向量,且,
(1)若,求的值;
(2)当时,求夹角的余弦值.
16.(本题满分12分)已知等比数列的前项和为,,,
(1)求等比数列的通项公式;
(2)令,证明数列为等差数列;
(3)对(2)中的数列,前项和为,求使最小时的的值.
17.(本题满分9分)已知,.
(1)化简,并求值.
(2)若,且,求及的值.
第二部分 能力检测(共50分)
四、填空题:本大题共2小题,每小题5分,共10分.
18.若数列满足,且,则通项________________.
19.课本介绍过平面向量数量积运算的几何意义:等于的长度与在方向上的投影的乘积. 运用几何意义,有时能得到更巧妙的解题思路. 例如:边长为1的正六边形ABCDEF中,点P是正六边形内的一点(含边界),则的取值范围是_____________.
五、解答题:本大题共3小题,共40分.解答应写出文字说明、证明过程或演算步骤.
20.(本题满分12分)在△ABC中,a、b、c分别是角A、B、C的对边,且.
(1)若,面积,求b+c的值;
(2)求的值(注意,此问只能使用题干的条件,不能用(1)问的条件).
21.(本题满分14分)设数列的前项和为,且.
(1)求数列的通项公式;
(2)若,为数列的前项和. 求;
(3)是否存在自然数,使得对一切恒成立?若存在,求出的值;若不存在,说明理由.
22.(本题满分14分)将一块圆心角为半径为a的扇形铁片截成一块矩形,如图,有两种裁法:
让矩形一边在扇形的一半径OA上(图1)或让矩形一边与弦AB平行(图2)
(1)在图1中,设矩形一边PM的长为,试把矩形PQRM的面积表示成关于x的函数;
(2)在图2中,设∠AOM =,试把矩形PQRM的面积表示成关于的函数;
(3)已知按图1的方案截得的矩形面积最大为,那么请问哪种裁法能得到最大面积的矩形?说明理由.
广东实验中学2011—2012学年高一级模块考试
数学 参考答案
第一部分 基础检测(共100分)
一、选择题:本大题共10小题,每小题5分,共50分
1、已知为等比数列,,则=( A )
A.16 B. C.4 D.
2、在中,,,,则的值为( C )
A. B. C. 或 D. 不存在
3、已知向量,,其中,函数的最大值为( D )
A. B. C. D.
4、设等差数列的前项和为,若,,则( B )
A.63 B.45 C.36 D.27
5、在中,a、b、c分别是角A、B、C的对边,若,则的形状是( A )
A.等腰三角形 B.等边三角形 C.直角三角形 D.锐角三角形
6、已知,,则的值为( C )
A. B. C. D.
7、数列的前项和为,则( D )
A. B.30 C.28 D.14
8、的值是( B )
A. B. C.1 D.
9、在数列中,,,则=( A )
A. B. C. D.
10、对于非零向量,下列运算中正确的有( D )个.
① ②
③ ④
A.3个 B.2个 C.1个 D.0个
二、填空题:本大题共4小题,每小题5分,共20分.
11、已知数列为等差数列,且,,则_____________.
11、已知,则=.
13、在中,a、b、c分别是角A、B、C的对边. 若,,则的外接圆半径等于_____________. 1
14、等差数列与等比数列之间是存在某种结构的类比关系的,例如从定义看,或者从通项公式看,都可以发现这种类比的原则. 按照此思想,请把下面等差数列的性质,类比到等比数列,写出相应的性质:
若为等差数列,,则公差;若是各项均为正数的等比数列,,则公比_________________.
三、解答题:本大题共3小题,共30分.
15、(本题满分9分)设,是两个相互垂直的单位向量,且,
(1)若,求的值;
(2)当时,求夹角的余弦值.
解:(1),,即 ……1分
化简得 ……2分
又,是两个相互垂直的单位向量,, ……3分
,. ……4分
(2)当时,
……5分
, ……7分
……9分
16、(本题满分12分)已知等比数列的前项和为,,,
(1)求等比数列的通项公式;
(2)令,证明数列为等差数列;
(3)对(2)中的数列,前项和为,求使最小时的的值.
解:(1), ,……2分
两式子相除得 , ……3分 代入解得,……4分
. ……5分
(2) ……6分
,为等差数列. ……8分
(3)方法一:令,得, ……10分
解得,……11分 当或时,前项和为最小. ……12分
方法二:, ……10分
对称轴方程为,……11分 当或时,前项和为最小. ……12分
17、(本题满分9分)已知,.
(1)化简,并求值.
(2)若,且,求及的值.
解:(1) ……2分
……3分
(2),, 又,
……5分
由,,得, ……6分
……7分
……9分
第二部分 能力检测(共50分)
四、选择题:本大题共2小题,每小题5分,共10分.
18、若数列满足,且,则通项________________.
19、课本介绍过平面向量数量积运算的几何意义:等于的长度与在方向上的投影的乘积. 运用几何意义,有时能得到更巧妙的解题思路. 例如:边长为1的正六边形ABCDEF中,点P是正六边形内的一点(含边界),则的取值范围是_____________.
五、解答题:本大题共3小题,共40分.解答应写出文字说明、证明过程或演算步骤.
20、(本题满分12分)在△ABC中,a、b、c分别是角A、B、C的对边,且.
(1)若,面积,求b+c的值;
(2)求的值(注意,此问只能使用题干的条件,不能用(1)问的条件).
解:(1),……1分 ……2分
由余弦定理 ……4分
得 ……5分
, ……6分
(2)由正弦定理知 ……8分
……10分
……12分
21、(本题满分14分)设数列的前项和为,且.
(1)求数列的通项公式;
(2)若,为数列的前项和. 求;
(3)是否存在自然数,使得对一切恒成立?若存在,求出的值;若不存在,说明理由.
解:(1)由,令,则,又,所以. ……1分
当时,由, ……2分
可得. 即. ……3分
所以是以为首项,为公比的等比数列,于是. ……4分
(2) ……5分
∴
……6分
∴. ……7分
, ……8分
从而.(写成也可) ……9分
(3),故单调递增
,又, ……11分
要恒成立,则, ……12分
解得,……13分 又,故. ……14分
22、(本题满分14分)将一块圆心角为半径为a的扇形铁片截成一块矩形,如图,有两种裁法:
让矩形一边在扇形的一半径OA上(图1)或让矩形一边与弦AB平行(图2)
(1)在图1中,设矩形一边PM的长为,试把矩形PQRM的面积表示成关于x的函数;
(2)在图2中,设∠AOM =,试把矩形PQRM的面积表示成关于的函数;
(3)已知按图1的方案截得的矩形面积最大为,那么请问哪种裁法能得到最大面积的矩形?说明理由.
解:(1)PM=QR=x,
在RT△QRO中,OR=
在RT△PMO中,OM=
RM=OM-OR=……2分
, ……3分
(2)∠MRA =×=,∠MRO =,
在△OMR中,由正弦定理,得:=,即RM = 2a·sin, ……6分
又=,∴OR = 2a·sin(-), ……8分
又正△ORQ中,QR=OR=2a·sin(-)
∴矩形的MPQR的面积为S= MR·PQ = 4a·sin·sin(-) ……9分
(3)对于(2)中的函数
……11分
当,即时, ……13分
,故按图1的方案能得到最大面积的矩形. ……14分
A
B
C
D
E
F
A
B
C
D
E
F
同课章节目录
