五年级数学上册 5.9实际问题与方程课件人教版(22张ppt)
文档属性
| 名称 | 五年级数学上册 5.9实际问题与方程课件人教版(22张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1006.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-13 12:19:00 | ||
图片预览







文档简介
(共22张PPT)
第5单元 简 易 方 程
实际问题与方程(3)
一、复习旧知,引入新课
1.解方程。
5x+6=26
2×14+2x=44
0.2x÷3=6
(2.8+x)×2=10.4
x=4
x=8
x=90
x=2.4
2.果园里有梨树35棵,橘子树的棵树是梨树的2倍,两种树一共多少棵?
35×2+35=105(棵)
答:两种树一共105棵。
3.(1)女同学有x人,男同学比女同学多12人,男同学有( )人。
(2)女同学有x人,男同学人数是女同学的2倍,男同学有( )人。
x+12
2x
二、合作交流,探索新知
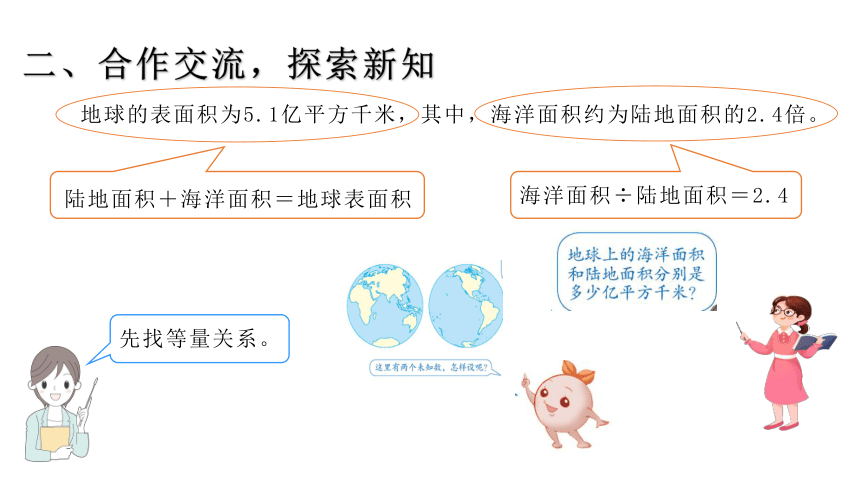
地球的表面积为5.1亿平方千米,其中,海洋面积约为陆地面积的2.4倍。
先找等量关系。
海洋面积÷陆地面积=2.4
陆地面积+海洋面积=地球表面积
陆地面积+海洋面积=地球表面积
(1)解:设陆地面积为x亿平方千米,
那么海洋面积为2.4x亿平方千米。
x+2.4x=5.1
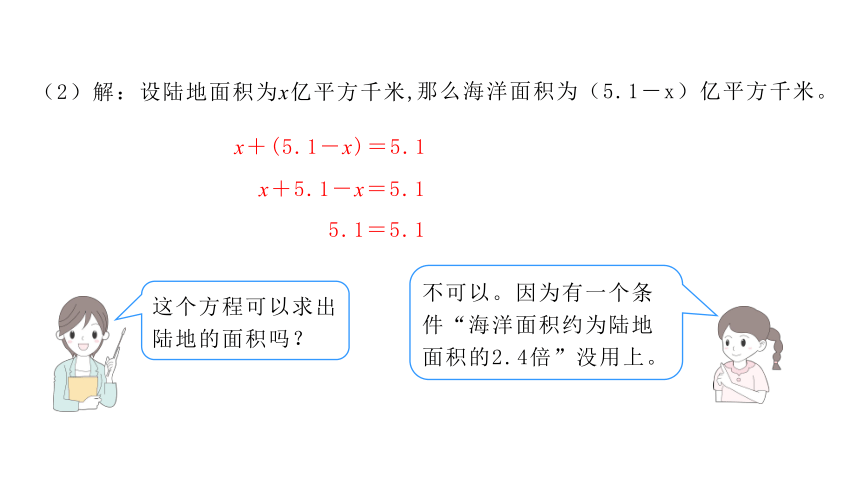
(2)解:设陆地面积为x亿平方千米,
那么海洋面积为(5.1-x)亿平方千米。
x+(5.1-x)=5.1
(3)解:设海洋面积为x亿平方千米,
那么陆地面积为2.4÷x亿平方千米。
x+x÷2.4=5.1
这三个方程都能正确求解吗?
陆地面积+海洋面积=地球表面积
(1)解:设陆地面积为x亿平方千米,
那么海洋面积为2.4x亿平方千米。
x+2.4x=5.1
(1+2.4)x=5.1
3.4x=5.1
3.4x÷3.4=5.1÷3.4
x=1.5
用了乘法分配律
5.1-1.5=3.6(亿平方千米)
或2.4x=2.4×1.5=3.6
海洋面积呢?
(2)解:设陆地面积为x亿平方千米,
那么海洋面积为(5.1-x)亿平方千米。
x+(5.1-x)=5.1
这个方程可以求出陆地的面积吗?
不可以。因为有一个条件“海洋面积约为陆地面积的2.4倍”没用上。
x+5.1-x=5.1
5.1=5.1
(3)解:设海洋面积为x亿平方千米,
那么陆地面积为x÷2.4亿平方千米。
x+x÷2.4=5.1
这个方程怎么解呢?
(x+x÷2.4)×2.4=5.1×2.4
2.4x+x=12.24
(2.4+1)x=12.24
3.4x=12.24
3.4x÷3.4=12.24÷3.4
x=3.6
陆地面积呢?
5.1-3.6=1.5(亿平方千米)
或x÷2.4=3.6÷2.4=1.5
海洋面积÷陆地面积=2.4
(2)解:设陆地面积为x亿平方千米,
那么海洋面积为2.4x亿平方千米。
(5.1-x)÷x=2.4
(1)解:设陆地面积为x亿平方千米,
那么海洋面积为(5.1-x)亿平方千米。
2.4x÷x=2.4
(3)解:设海洋面积为x亿平方千米,
那么陆地面积为(5.1-x)亿平方千米。
x÷(5.1-x) =2.4
这三个方程都能正确求解吗?试着求解看看。
陆地面积+海洋面积=地球表面积
海洋面积÷陆地面积=2.4
如何检验呢?
1.5+3.6=5.1(亿平方千米)
3.6÷2.4=1.5
要同时满足这两个条件,才能说明这道题做对了。
小结:
如果要选择一个方程,你会选择哪一个?
第一个,列式最顺而且求解方便。
遇到差倍问题时,一般设倍数关系中“的”前面的量为x,然后根据倍数关系表示出另一个量,再根据和(差)关系列出方程。
x+2.4x=5.1
(1+2.4)x=5.1
3.4x=5.1
3.4x÷3.4=5.1÷3.4
x=1.5
5.1-1.5=3.6(亿平方千米)
或2.4x=2.4×1.5=3.6
解:设陆地面积为x亿平方千米,那么海洋面积为2.4x亿平方千米。
三、巩固练习,学以致用
(一)基础练习
果园里种着桃树和杏树,杏树的棵树是桃树的3倍。
解:设桃树有x棵,则杏树有3x棵。
解得 x=45
x+3x=180
答:桃树有45棵,杏树有135棵。
桃树总数+杏树总数=180棵
(1)桃树和杏树一共有180棵,桃树和杏树各有多少棵?
则3x=3×45=135
或180-45=135(棵)
(2)杏树比桃树多90棵,桃树和杏树各有多少棵?
(二)拓展应用:配套P49
解:设桃树有x棵,则杏树有3x棵。
解得 x=45
3x-x=90
答:桃树有45棵,杏树有135棵。
杏树总数-桃树总数=90棵
则3x=3×45=135
或180-45=135(棵)
四、总结归纳
总结:遇到差倍问题时,一般设倍数关系中“的”前面的量为x,然后根据倍数关系表示出另一个量,再根据和(差)关系列出方程。
第二课时
一、复习旧知,引入新课
小红每分钟走60 m,小花每分钟走70 m。
①小红5分钟走多少米?
②小花5分钟走多少米?
③小红和小花5分钟共走多少米?
④小红比小花5分钟少走多少米?
依据:
速度×时间=路程
路程÷时间=速度
路程÷速度=时间
60×5=300(m)
70×5=350(m)
60×5+70×5=650(m)
70×5-60×5=50(m)
这个公式可以怎么变形?
二、合作交流,探索新知
小林家和小云家相距4.5 km。周日早上9:00 两人分别从家骑自行车相向而行,两人何时相遇?
可画线段图分析数量关系。
4.5 km
小林骑的路程
线段图:
0.25千米/分
0.2千米/分
小云骑的路程
小林骑的路程+小云骑的路程=总路程
解:设两人x分钟后相遇。
0.25x+0.2x=4.5
0.45x=4.5
0.45x÷0.45=4.5÷0.45
x=10
解:设两人x分钟后相遇。
0.25x+0.2x=4.5
0.45x=4.5
0.45x÷0.45=4.5÷0.45
x=10
答:两人9:10相遇。
两人何时相遇呢?
10分钟后,也就是9:10。
检验一下!
小林骑的路程+小云骑的路程=总路程
0.25×10+0.2×10=4.5=总路程
三、巩固练习,学以致用
(一)基础练习
1.两列火车从相距570 km的两地同时相向开出。甲车每小时行110 km,乙车每小时行80km。经过几小时两车相遇?
解:设经过x小时两车相遇。
解得 x=3
110x+80x=570
答:经过3小时两车相遇。
甲车的路程+乙车的路程=总路程
2.
(二)拓展应用:配套P50
解:设乙队每天开凿x m。
解得 x=14.4
12.6×25+25x=675
答:乙队每天开凿14.4 m。
两个工程队同时开凿一条675 m长的隧道,各从一端相向施工,25天打通。甲队每天开凿12.6 m,乙队每天开凿多少米?
甲队的工作量+乙队的工作量=总工作量
四、总结归纳
总结:通过画线段图可以清楚分析遇到问题中的数量关系之间的等量关系,一般用甲的路程+乙的路程=总路程来列方程解答。
第5单元 简 易 方 程
实际问题与方程(3)
一、复习旧知,引入新课
1.解方程。
5x+6=26
2×14+2x=44
0.2x÷3=6
(2.8+x)×2=10.4
x=4
x=8
x=90
x=2.4
2.果园里有梨树35棵,橘子树的棵树是梨树的2倍,两种树一共多少棵?
35×2+35=105(棵)
答:两种树一共105棵。
3.(1)女同学有x人,男同学比女同学多12人,男同学有( )人。
(2)女同学有x人,男同学人数是女同学的2倍,男同学有( )人。
x+12
2x
二、合作交流,探索新知
地球的表面积为5.1亿平方千米,其中,海洋面积约为陆地面积的2.4倍。
先找等量关系。
海洋面积÷陆地面积=2.4
陆地面积+海洋面积=地球表面积
陆地面积+海洋面积=地球表面积
(1)解:设陆地面积为x亿平方千米,
那么海洋面积为2.4x亿平方千米。
x+2.4x=5.1
(2)解:设陆地面积为x亿平方千米,
那么海洋面积为(5.1-x)亿平方千米。
x+(5.1-x)=5.1
(3)解:设海洋面积为x亿平方千米,
那么陆地面积为2.4÷x亿平方千米。
x+x÷2.4=5.1
这三个方程都能正确求解吗?
陆地面积+海洋面积=地球表面积
(1)解:设陆地面积为x亿平方千米,
那么海洋面积为2.4x亿平方千米。
x+2.4x=5.1
(1+2.4)x=5.1
3.4x=5.1
3.4x÷3.4=5.1÷3.4
x=1.5
用了乘法分配律
5.1-1.5=3.6(亿平方千米)
或2.4x=2.4×1.5=3.6
海洋面积呢?
(2)解:设陆地面积为x亿平方千米,
那么海洋面积为(5.1-x)亿平方千米。
x+(5.1-x)=5.1
这个方程可以求出陆地的面积吗?
不可以。因为有一个条件“海洋面积约为陆地面积的2.4倍”没用上。
x+5.1-x=5.1
5.1=5.1
(3)解:设海洋面积为x亿平方千米,
那么陆地面积为x÷2.4亿平方千米。
x+x÷2.4=5.1
这个方程怎么解呢?
(x+x÷2.4)×2.4=5.1×2.4
2.4x+x=12.24
(2.4+1)x=12.24
3.4x=12.24
3.4x÷3.4=12.24÷3.4
x=3.6
陆地面积呢?
5.1-3.6=1.5(亿平方千米)
或x÷2.4=3.6÷2.4=1.5
海洋面积÷陆地面积=2.4
(2)解:设陆地面积为x亿平方千米,
那么海洋面积为2.4x亿平方千米。
(5.1-x)÷x=2.4
(1)解:设陆地面积为x亿平方千米,
那么海洋面积为(5.1-x)亿平方千米。
2.4x÷x=2.4
(3)解:设海洋面积为x亿平方千米,
那么陆地面积为(5.1-x)亿平方千米。
x÷(5.1-x) =2.4
这三个方程都能正确求解吗?试着求解看看。
陆地面积+海洋面积=地球表面积
海洋面积÷陆地面积=2.4
如何检验呢?
1.5+3.6=5.1(亿平方千米)
3.6÷2.4=1.5
要同时满足这两个条件,才能说明这道题做对了。
小结:
如果要选择一个方程,你会选择哪一个?
第一个,列式最顺而且求解方便。
遇到差倍问题时,一般设倍数关系中“的”前面的量为x,然后根据倍数关系表示出另一个量,再根据和(差)关系列出方程。
x+2.4x=5.1
(1+2.4)x=5.1
3.4x=5.1
3.4x÷3.4=5.1÷3.4
x=1.5
5.1-1.5=3.6(亿平方千米)
或2.4x=2.4×1.5=3.6
解:设陆地面积为x亿平方千米,那么海洋面积为2.4x亿平方千米。
三、巩固练习,学以致用
(一)基础练习
果园里种着桃树和杏树,杏树的棵树是桃树的3倍。
解:设桃树有x棵,则杏树有3x棵。
解得 x=45
x+3x=180
答:桃树有45棵,杏树有135棵。
桃树总数+杏树总数=180棵
(1)桃树和杏树一共有180棵,桃树和杏树各有多少棵?
则3x=3×45=135
或180-45=135(棵)
(2)杏树比桃树多90棵,桃树和杏树各有多少棵?
(二)拓展应用:配套P49
解:设桃树有x棵,则杏树有3x棵。
解得 x=45
3x-x=90
答:桃树有45棵,杏树有135棵。
杏树总数-桃树总数=90棵
则3x=3×45=135
或180-45=135(棵)
四、总结归纳
总结:遇到差倍问题时,一般设倍数关系中“的”前面的量为x,然后根据倍数关系表示出另一个量,再根据和(差)关系列出方程。
第二课时
一、复习旧知,引入新课
小红每分钟走60 m,小花每分钟走70 m。
①小红5分钟走多少米?
②小花5分钟走多少米?
③小红和小花5分钟共走多少米?
④小红比小花5分钟少走多少米?
依据:
速度×时间=路程
路程÷时间=速度
路程÷速度=时间
60×5=300(m)
70×5=350(m)
60×5+70×5=650(m)
70×5-60×5=50(m)
这个公式可以怎么变形?
二、合作交流,探索新知
小林家和小云家相距4.5 km。周日早上9:00 两人分别从家骑自行车相向而行,两人何时相遇?
可画线段图分析数量关系。
4.5 km
小林骑的路程
线段图:
0.25千米/分
0.2千米/分
小云骑的路程
小林骑的路程+小云骑的路程=总路程
解:设两人x分钟后相遇。
0.25x+0.2x=4.5
0.45x=4.5
0.45x÷0.45=4.5÷0.45
x=10
解:设两人x分钟后相遇。
0.25x+0.2x=4.5
0.45x=4.5
0.45x÷0.45=4.5÷0.45
x=10
答:两人9:10相遇。
两人何时相遇呢?
10分钟后,也就是9:10。
检验一下!
小林骑的路程+小云骑的路程=总路程
0.25×10+0.2×10=4.5=总路程
三、巩固练习,学以致用
(一)基础练习
1.两列火车从相距570 km的两地同时相向开出。甲车每小时行110 km,乙车每小时行80km。经过几小时两车相遇?
解:设经过x小时两车相遇。
解得 x=3
110x+80x=570
答:经过3小时两车相遇。
甲车的路程+乙车的路程=总路程
2.
(二)拓展应用:配套P50
解:设乙队每天开凿x m。
解得 x=14.4
12.6×25+25x=675
答:乙队每天开凿14.4 m。
两个工程队同时开凿一条675 m长的隧道,各从一端相向施工,25天打通。甲队每天开凿12.6 m,乙队每天开凿多少米?
甲队的工作量+乙队的工作量=总工作量
四、总结归纳
总结:通过画线段图可以清楚分析遇到问题中的数量关系之间的等量关系,一般用甲的路程+乙的路程=总路程来列方程解答。
