小学数学人教版五年级上5.5解 方 程 课件(25张ppt)
文档属性
| 名称 | 小学数学人教版五年级上5.5解 方 程 课件(25张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-13 12:25:57 | ||
图片预览





文档简介
第5单元 简 易 方 程
解 方 程(1)
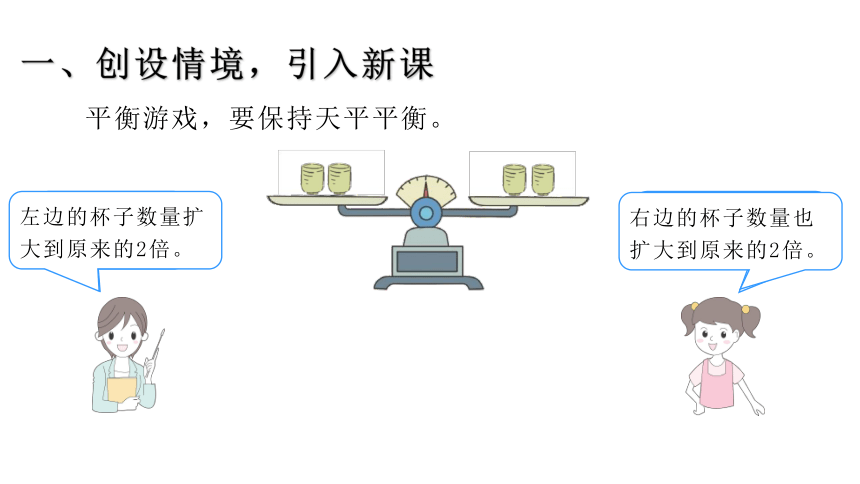
一、创设情境,引入新课
我在右边添加一个相同的杯子。
我在左边添加一个杯子。
平衡游戏,要保持天平平衡。
右边的杯子数量也扩大到原来的2倍。
左边的杯子数量扩大到原来的2倍。
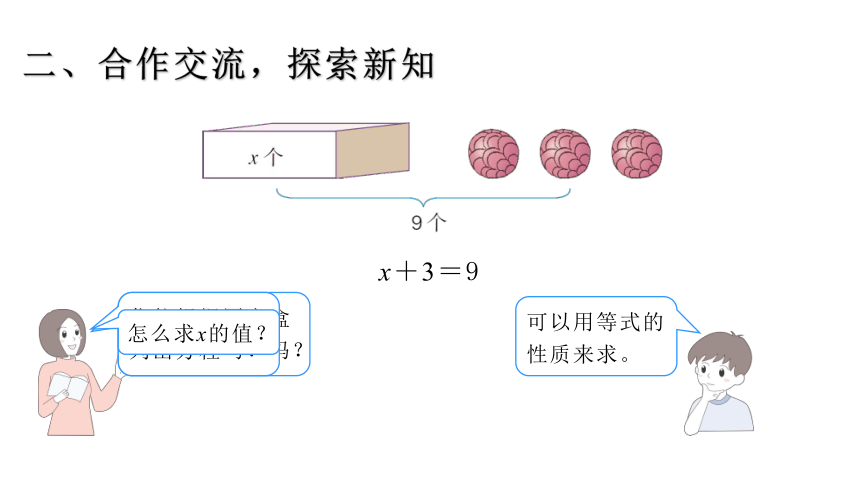
二、合作交流,探索新知
你能准确说出盒子里有几个球吗?
x+3=9
你能根据图意列出方程吗?
怎么求x的值?
可以用等式的性质来求。
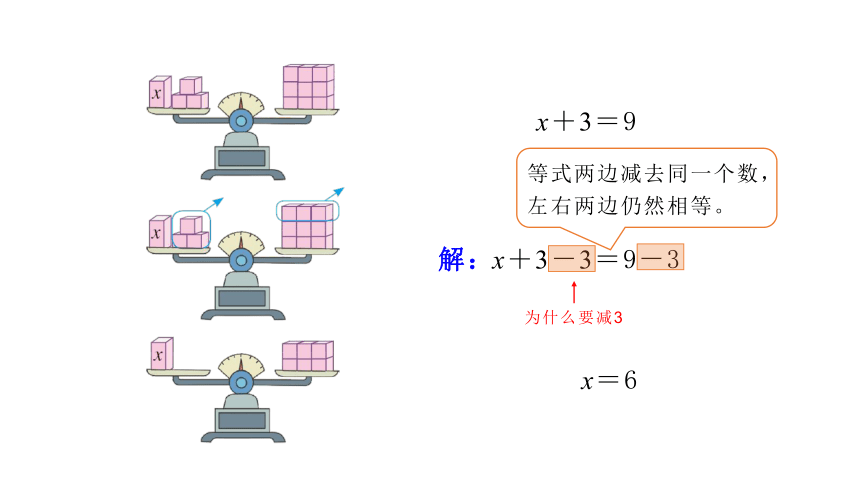
x+3=9
x+3-3=9-3
x=6
等式两边减去同一个数,左右两边仍然相等。
为什么要减3
解:
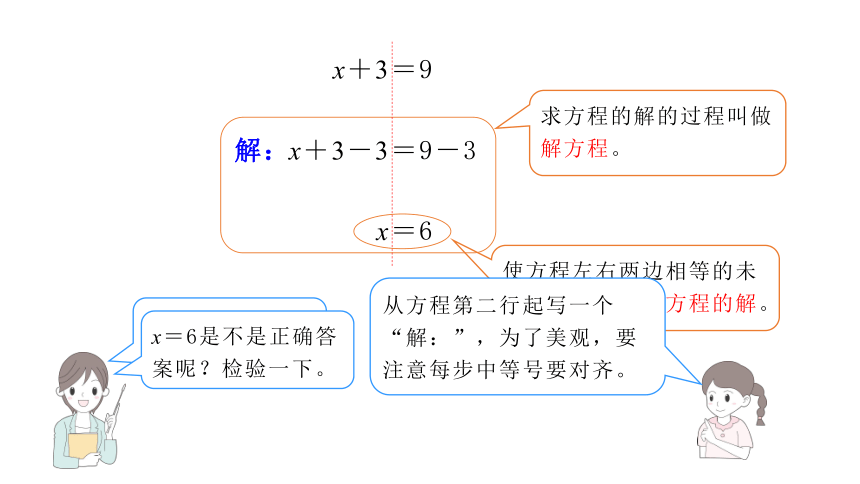
x+3=9
x+3-3=9-3
x=6
解:
使方程左右两边相等的未知数的值,叫做方程的解。
求方程的解的过程叫做解方程。
解方程的书写格式有什么要求?
从方程第二行起写一个“解:”,为了美观,要注意每步中等号要对齐。
x=6是不是正确答案呢?检验一下。
方程的左边=x+3
=6+3
=9
=方程的右边
所以,x=6是方程的解。
x+3=9
x+3-3=9-3
x=6
解:
x=6是不是正确答案呢?检验一下。
三、巩固练习,学以致用
(一)基础练习
1.解方程。
(1)100+x=250
(2)x+12=31
(3)x-63=36
解:100+x-100=250-100
x=150
解:x+12-12=31-12
x=99
解:x-63+63=36+63
x=19
2.x=2是方程5x=15的解吗?x=3呢?
(二)拓展应用:配套P42
方程的左边=5x
=5×2
=10
≠方程的右边
所以,x=2不是方程的解。
方程的左边=5x
=5×3
=15
=方程的右边
所以,x=3是方程的解。
四、总结归纳
1.解方程是根据等式的性质来解。
2.使方程左右两边相等的未知数的值,叫做方程的解。
3.求方程解的过程叫做解方程。
第二课时
一、复习旧知,引入新课
1.列方程并解答。
2.解方程。
(1)200+x=310
(2)x-45=23
解:x+1.2-1.2=4-1.2
x=2.8
解:200+x-200=310-200
x=110
x+1.2=4
解:x-45+45=23+45
x=68
二、合作交流,探索新知
解方程3x=18。
3x=18
3x÷( )=18÷( )
解:
x=( )
等式两边除以同一个不为0的数,左右两边仍然相等。
为什么除以3?
3
3
6
请你检验一下。
3x=18
3x÷( )=18÷( )
解:
x=( )
为什么除以3?
3
3
6
请你检验一下。
方程的左边=3x
=3×6
=18
=方程的右边
所以,x=6是方程的解。
解方程20-x=9。
x=11
20-x+x=9+x
20=9+x
9+x=20
9+x-9=20-9
等式两边加上相同的式子,左右两边仍然相等。
方程的左边=20-x
=20-11
=9
=方程的右边
所以,x=11是方程的解。
解:
等式两边相等,可以把它们的位置交换。
请你检验一下。
三、巩固练习,学以致用
(一)基础练习
x=1.4
x=13
x=5.8
1.解方程。
x+3.2=4.6
x-1.8=4
15-x=2
1.6x=6.4
x÷7=0.3
2.1÷x=3
x=4
x=0.7
x=2.1
2.后面括号中哪个x的值是方程的解?
(二)拓展应用:配套P43
(1)x+32=76
(2)12-x=4
(3)4x=6
(4)3÷x=1.5
(x=44,x=108)
(x=16,x=8)
(x=1.5,x=2)
(x=0.5,x=2)
四、总结归纳
总结:学会了解形如ax=b和a-x=b的方程的方法,知道了x在等式右边时,可以交换等式两边的位置。
第三课时
一、复习旧知,引入新课
解下面方程。
(1)4x=36
(2)12-x=8
解:4x÷4=36÷4
x=9
解:12-x+x=8+x
12=8+x
8+x=12
8+x-8=12-8
x=4
二、合作交流,探索新知
看图列方程,并求出方程的解。
3x+4=40
解:
3x+4-4=40-4
先把3x看做一个整体。
3x=36
3x÷3=36÷3
3x=12
解方程 2(x-16)=8。
2(x-16)÷2=8÷2
解:
先把(x-16)看做一个整体。
x-16=4
x-16+16=4+16
x=20
还可以怎么算?
2x-32=8
解:
解方程 2(x-16)=8。
运用了乘法分配律
先把2x看做一个整体。
2x-32+32=8+32
2x=40
2x÷2=40÷2
x=20
别忘了检验!
方程的左边=2(x-16)
=2×(20-16)
=2×4
=方程的右边
所以,x=20是方程的解。
=8
三、巩固练习,学以致用
(一)基础练习
x=8
x=26
1.解下列方程。
6x-35=13
3x-12×6=6
(5x-12)×8=24
(100-3x)÷2=8
x=3
x=28
2.解下列方程。
(二)拓展应用:配套P44
6x+3=9
4x-2=10
5x-39=56
x=1
x=3
x=19
18+5x=21
8x-4×14=0
7x÷3=8.19
x=0.6
x=7
x=3.51
四、总结归纳
1.在解较复杂的方程时,可以把一个式子看作一个整体来解。
2.在解方程时,可以运用运算定律来解。
解 方 程(1)
一、创设情境,引入新课
我在右边添加一个相同的杯子。
我在左边添加一个杯子。
平衡游戏,要保持天平平衡。
右边的杯子数量也扩大到原来的2倍。
左边的杯子数量扩大到原来的2倍。
二、合作交流,探索新知
你能准确说出盒子里有几个球吗?
x+3=9
你能根据图意列出方程吗?
怎么求x的值?
可以用等式的性质来求。
x+3=9
x+3-3=9-3
x=6
等式两边减去同一个数,左右两边仍然相等。
为什么要减3
解:
x+3=9
x+3-3=9-3
x=6
解:
使方程左右两边相等的未知数的值,叫做方程的解。
求方程的解的过程叫做解方程。
解方程的书写格式有什么要求?
从方程第二行起写一个“解:”,为了美观,要注意每步中等号要对齐。
x=6是不是正确答案呢?检验一下。
方程的左边=x+3
=6+3
=9
=方程的右边
所以,x=6是方程的解。
x+3=9
x+3-3=9-3
x=6
解:
x=6是不是正确答案呢?检验一下。
三、巩固练习,学以致用
(一)基础练习
1.解方程。
(1)100+x=250
(2)x+12=31
(3)x-63=36
解:100+x-100=250-100
x=150
解:x+12-12=31-12
x=99
解:x-63+63=36+63
x=19
2.x=2是方程5x=15的解吗?x=3呢?
(二)拓展应用:配套P42
方程的左边=5x
=5×2
=10
≠方程的右边
所以,x=2不是方程的解。
方程的左边=5x
=5×3
=15
=方程的右边
所以,x=3是方程的解。
四、总结归纳
1.解方程是根据等式的性质来解。
2.使方程左右两边相等的未知数的值,叫做方程的解。
3.求方程解的过程叫做解方程。
第二课时
一、复习旧知,引入新课
1.列方程并解答。
2.解方程。
(1)200+x=310
(2)x-45=23
解:x+1.2-1.2=4-1.2
x=2.8
解:200+x-200=310-200
x=110
x+1.2=4
解:x-45+45=23+45
x=68
二、合作交流,探索新知
解方程3x=18。
3x=18
3x÷( )=18÷( )
解:
x=( )
等式两边除以同一个不为0的数,左右两边仍然相等。
为什么除以3?
3
3
6
请你检验一下。
3x=18
3x÷( )=18÷( )
解:
x=( )
为什么除以3?
3
3
6
请你检验一下。
方程的左边=3x
=3×6
=18
=方程的右边
所以,x=6是方程的解。
解方程20-x=9。
x=11
20-x+x=9+x
20=9+x
9+x=20
9+x-9=20-9
等式两边加上相同的式子,左右两边仍然相等。
方程的左边=20-x
=20-11
=9
=方程的右边
所以,x=11是方程的解。
解:
等式两边相等,可以把它们的位置交换。
请你检验一下。
三、巩固练习,学以致用
(一)基础练习
x=1.4
x=13
x=5.8
1.解方程。
x+3.2=4.6
x-1.8=4
15-x=2
1.6x=6.4
x÷7=0.3
2.1÷x=3
x=4
x=0.7
x=2.1
2.后面括号中哪个x的值是方程的解?
(二)拓展应用:配套P43
(1)x+32=76
(2)12-x=4
(3)4x=6
(4)3÷x=1.5
(x=44,x=108)
(x=16,x=8)
(x=1.5,x=2)
(x=0.5,x=2)
四、总结归纳
总结:学会了解形如ax=b和a-x=b的方程的方法,知道了x在等式右边时,可以交换等式两边的位置。
第三课时
一、复习旧知,引入新课
解下面方程。
(1)4x=36
(2)12-x=8
解:4x÷4=36÷4
x=9
解:12-x+x=8+x
12=8+x
8+x=12
8+x-8=12-8
x=4
二、合作交流,探索新知
看图列方程,并求出方程的解。
3x+4=40
解:
3x+4-4=40-4
先把3x看做一个整体。
3x=36
3x÷3=36÷3
3x=12
解方程 2(x-16)=8。
2(x-16)÷2=8÷2
解:
先把(x-16)看做一个整体。
x-16=4
x-16+16=4+16
x=20
还可以怎么算?
2x-32=8
解:
解方程 2(x-16)=8。
运用了乘法分配律
先把2x看做一个整体。
2x-32+32=8+32
2x=40
2x÷2=40÷2
x=20
别忘了检验!
方程的左边=2(x-16)
=2×(20-16)
=2×4
=方程的右边
所以,x=20是方程的解。
=8
三、巩固练习,学以致用
(一)基础练习
x=8
x=26
1.解下列方程。
6x-35=13
3x-12×6=6
(5x-12)×8=24
(100-3x)÷2=8
x=3
x=28
2.解下列方程。
(二)拓展应用:配套P44
6x+3=9
4x-2=10
5x-39=56
x=1
x=3
x=19
18+5x=21
8x-4×14=0
7x÷3=8.19
x=0.6
x=7
x=3.51
四、总结归纳
1.在解较复杂的方程时,可以把一个式子看作一个整体来解。
2.在解方程时,可以运用运算定律来解。
