小学数学人教版五年级上5.7实际问题与方程 课件(31张ppt)
文档属性
| 名称 | 小学数学人教版五年级上5.7实际问题与方程 课件(31张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-13 00:00:00 | ||
图片预览









文档简介
第5单元 简 易 方 程
实际问题与方程(1)
一、复习旧知,引入新课
用方程表示下面的等量关系,并解方程。
(1)2个x的和是10。
解:2x÷2=10÷2
x=5
2x=10
解:x-6.2+6.2=2.3+6.2
x=8.5
(3)x的2.5倍是20。
x-6.2=2.3
(2)x比6.2多2.3。
解:2.5x÷2.5=20÷2.5
x=8
2.5x=20
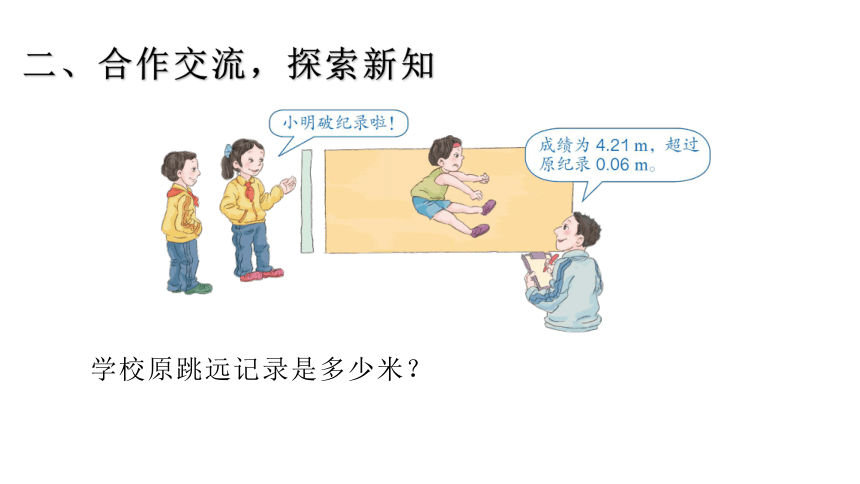
二、合作交流,探索新知
学校原跳远记录是多少米?
0.06 m
?米
原纪录
小 明
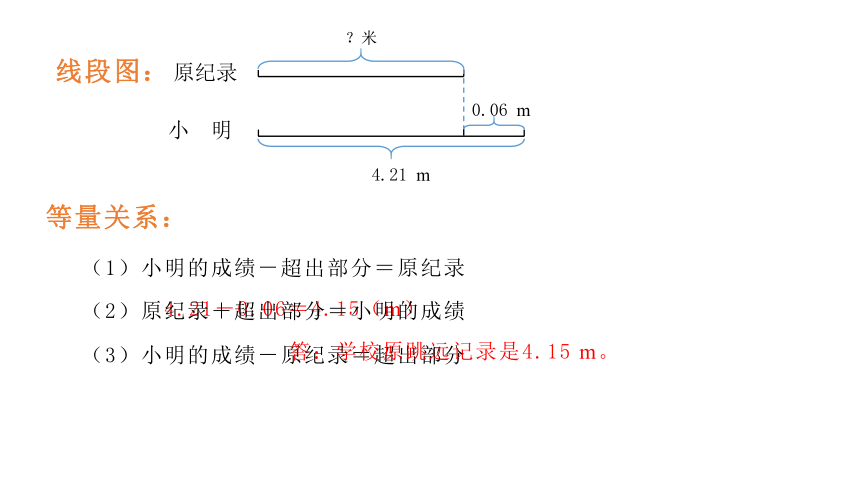
线段图:
4.21 m
4.21-0.06=4.15(m)
等量关系:
(1)小明的成绩-超出部分=原纪录
(2)原纪录+超出部分=小明的成绩
(3)小明的成绩-原纪录=超出部分
答:学校原跳远记录是4.15 m。
等量关系:
(2)原纪录+超出部分=小明的成绩
(3)小明的成绩-原纪录=超出部分
解:设学校原跳远记录是x m。
x=4.15
x+0.06=4.21
x+0.06-0.06=4.21-0.06
答:学校原跳远记录是4.15 m。
等量关系:
(3)小明的成绩-原纪录=超出部分
解:设学校原跳远记录是x m。
x=4.15
4.21-x=0.06
x=4.21-0.06
答:学校原跳远记录是4.15 m。
别忘了检验!
小结:
我们分别用了什么方法解决问题?
我们用了算术的方法和列方程解答。
用方程的思路解决问题,你认为什么是关键?
找出等量关系。
方程解法和算术解法有什么区别?
方程解法中未知数用字母表示,参与列式;算术解法中未知数不参与列式。
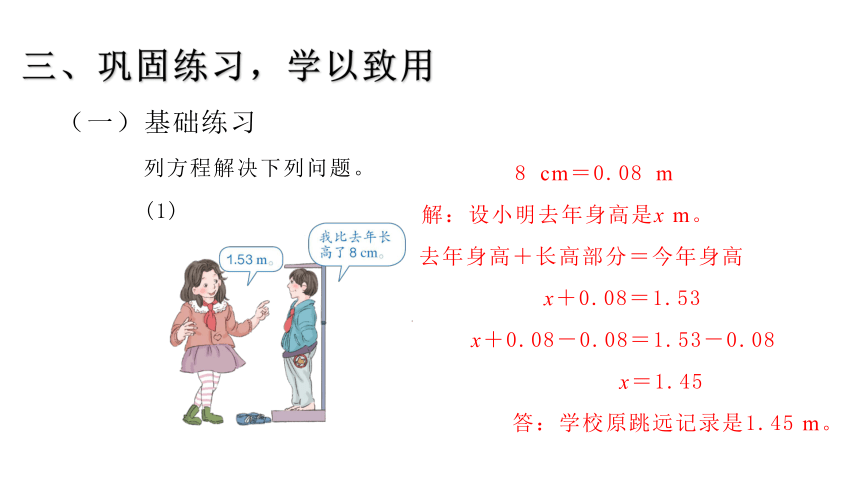
三、巩固练习,学以致用
(一)基础练习
列方程解决下列问题。
(1)
解:设小明去年身高是x m。
x=1.45
x+0.08=1.53
x+0.08-0.08=1.53-0.08
答:学校原跳远记录是1.45 m。
8 cm=0.08 m
去年身高+长高部分=今年身高
(2)
(二)拓展应用:配套P46
解:设每分钟浪费x kg。
x=0.06
30x=1.8
答:每分钟浪费0.06 kg。
半小时=30分
30x÷30=1.8÷30
30×每分钟滴的水=半小时滴的水
四、总结归纳
总结:列方程解应用题,关键是要找出题目中的等量关系,根据等量关系式设未知数,然后再列方程求解。
第二课时
一、复习旧知,引入新课
1.解方程。
x=25
x+20=45
x÷4=7
x-3=15
3x=24
x=28
x=18
x=8
解:x+20-20=45-20
解:x÷4×4=7×4
解:x-3+3=15+3
解:3x÷3=24÷3
2.找出问题中的等量关系。
老师昨天买的圆珠笔是x元,钢笔12元,钢笔的价格比圆珠笔的3倍还多1元。
1元
x元
圆珠笔
钢 笔
线段图:
12元
等量关系:
(1)圆珠笔的价格×3+1=钢笔的价格
(2)圆珠笔的价格×3=钢笔的价格-1
(4)(钢笔的价格-1)÷3=圆珠笔的价格
(3)钢笔的价格-圆珠笔的价格×3=1
线段图有什么好处?
直观、形象,让我们更容易找到等量关系。
二、合作交流,探索新知
等量关系:
(1)黑色皮块数×2-4=白色皮块数
(2)黑色皮块数×2-白色皮块数=4
(3)黑色皮块数×2=白色皮块数+4
线段图:
20块
?块
黑色皮
白色皮
4块
(4)(白色皮块数+4)÷2=黑色皮块数
等量关系:
(1)黑色皮块数×2-4=白色皮块数
(2)黑色皮块数×2-白色皮块数=4
(3)黑色皮块数×2=白色皮块数+4
(4)(白色皮块数+4)÷2=黑色皮块数
2x-4=20
2x-20=4
2x=20+4
(20+4)÷2
=12(块)
解:设共有x块黑色皮。
解:设共有x块黑色皮。
解:设共有x块黑色皮。
等量关系:
(1)黑色皮块数×2-4=白色皮块数
2x-4=20
解:设共有x块黑色皮。
2x-4+4=20+4
2x=24
x=12
2x÷2=24÷2
先把2x看做一个整体。
答:设共有12块黑色皮。
(2)黑色皮块数×2-白色皮块数=4
(3)黑色皮块数×2=白色皮块数+4
2x-20=4
2x=20+4
解:设共有x块黑色皮。
解:设共有x块黑色皮。
同学们独立解答,看看计算结果是否一致。
检验计算结果是否正确。
x=12
x=12
1.找出未知数,用字母x表示;
小结:列方程解决实际问题的步骤
2.分析实际问题中的数量关系,找出等量关系,列方程;
3.解方程并检验作答。
三、巩固练习,学以致用
(一)基础练习
1.共有1428个网球,每5个装一筒,装完后还剩3个。一共装了多少筒?
解:设一共装了x筒。
解得 x=285
5x+3=1428
答:一共装了285筒。
每筒网球的个数×筒数+3=网球总数
2.故宫的面积是72万平方米,比天安门广场面积的2倍少16万平方米。天安门广场的面积是多少万平方米?
(二)拓展应用:配套P47
解:设天安门广场的面积是x万平方米。
解得x=44
答:天安门广场的面积是44万平方米。
天安门广场的面积×2-16=故宫的面积
2x-16=72
四、总结归纳
1.找出未知数,用字母x表示;
2.分析实际问题中的数量关系,找出等量关系,列方程;
3.解方程并检验作答。
第三课时
一、复习旧知,引入新课
只列式不计算。
22×8+25×8
商店运来苹果和梨各8筐,每筐苹果重25 kg,每筐梨重22 kg,苹果和梨共重多少千克?
或
(22+25)×8
两个式子有什么不同?
二、合作交流,探索新知
梨每千克2.8元,苹果每千克多少钱?
解:设苹果每千克x元。
x=2.4
2.8×2
答:苹果每千克2.4元。
苹果的总价+梨的总价=总价钱
2x
=
+
10.4
2x+5.6=10.4
2x+5.6-5.6=10.4-5.6
2x=4.8
2x÷2=4.8÷2
两种水果的单价和×2=总价钱
×2
=
(x+2.8)
10.4
(2.8+x)×2÷2=10.4÷2
2.8+x=5.2
2.8+x-2.8=5.2-2.8
x=2.4
看做一个整体。
怎样检验结果是否正确?
苹果的总价+梨的总价=总价钱
两种水果的单价和×2=总价钱
2×2.4+2.8×2=10.4=总价钱
(2.8+2.4)×2=10.4=总价钱
三、巩固练习,学以致用
(一)基础练习
1.
解:设儿童票每张x元。
解得 x=1.5
2x+2×4=11
答:儿童票每张1.5元。
成人票价总和+儿童票价总和=11元
《科学家》丛书有4本,《发明家》丛书有多少本?
(二)拓展应用:配套P48
解:设《发明家》丛书有x本。
解得x=3
答:《发明家》丛书有3本。
4x+2.5×4=22
我买了两套丛书,共花了22元。
2.
《科学家》丛书的总价+《发明家》丛书的总价=11元
四、总结归纳
总结:学会了解形如ax+ab=c的方程,明白乘法分配律也可以运用到解方程中,还知道有些实际问题不止一种列方程的方法。
实际问题与方程(1)
一、复习旧知,引入新课
用方程表示下面的等量关系,并解方程。
(1)2个x的和是10。
解:2x÷2=10÷2
x=5
2x=10
解:x-6.2+6.2=2.3+6.2
x=8.5
(3)x的2.5倍是20。
x-6.2=2.3
(2)x比6.2多2.3。
解:2.5x÷2.5=20÷2.5
x=8
2.5x=20
二、合作交流,探索新知
学校原跳远记录是多少米?
0.06 m
?米
原纪录
小 明
线段图:
4.21 m
4.21-0.06=4.15(m)
等量关系:
(1)小明的成绩-超出部分=原纪录
(2)原纪录+超出部分=小明的成绩
(3)小明的成绩-原纪录=超出部分
答:学校原跳远记录是4.15 m。
等量关系:
(2)原纪录+超出部分=小明的成绩
(3)小明的成绩-原纪录=超出部分
解:设学校原跳远记录是x m。
x=4.15
x+0.06=4.21
x+0.06-0.06=4.21-0.06
答:学校原跳远记录是4.15 m。
等量关系:
(3)小明的成绩-原纪录=超出部分
解:设学校原跳远记录是x m。
x=4.15
4.21-x=0.06
x=4.21-0.06
答:学校原跳远记录是4.15 m。
别忘了检验!
小结:
我们分别用了什么方法解决问题?
我们用了算术的方法和列方程解答。
用方程的思路解决问题,你认为什么是关键?
找出等量关系。
方程解法和算术解法有什么区别?
方程解法中未知数用字母表示,参与列式;算术解法中未知数不参与列式。
三、巩固练习,学以致用
(一)基础练习
列方程解决下列问题。
(1)
解:设小明去年身高是x m。
x=1.45
x+0.08=1.53
x+0.08-0.08=1.53-0.08
答:学校原跳远记录是1.45 m。
8 cm=0.08 m
去年身高+长高部分=今年身高
(2)
(二)拓展应用:配套P46
解:设每分钟浪费x kg。
x=0.06
30x=1.8
答:每分钟浪费0.06 kg。
半小时=30分
30x÷30=1.8÷30
30×每分钟滴的水=半小时滴的水
四、总结归纳
总结:列方程解应用题,关键是要找出题目中的等量关系,根据等量关系式设未知数,然后再列方程求解。
第二课时
一、复习旧知,引入新课
1.解方程。
x=25
x+20=45
x÷4=7
x-3=15
3x=24
x=28
x=18
x=8
解:x+20-20=45-20
解:x÷4×4=7×4
解:x-3+3=15+3
解:3x÷3=24÷3
2.找出问题中的等量关系。
老师昨天买的圆珠笔是x元,钢笔12元,钢笔的价格比圆珠笔的3倍还多1元。
1元
x元
圆珠笔
钢 笔
线段图:
12元
等量关系:
(1)圆珠笔的价格×3+1=钢笔的价格
(2)圆珠笔的价格×3=钢笔的价格-1
(4)(钢笔的价格-1)÷3=圆珠笔的价格
(3)钢笔的价格-圆珠笔的价格×3=1
线段图有什么好处?
直观、形象,让我们更容易找到等量关系。
二、合作交流,探索新知
等量关系:
(1)黑色皮块数×2-4=白色皮块数
(2)黑色皮块数×2-白色皮块数=4
(3)黑色皮块数×2=白色皮块数+4
线段图:
20块
?块
黑色皮
白色皮
4块
(4)(白色皮块数+4)÷2=黑色皮块数
等量关系:
(1)黑色皮块数×2-4=白色皮块数
(2)黑色皮块数×2-白色皮块数=4
(3)黑色皮块数×2=白色皮块数+4
(4)(白色皮块数+4)÷2=黑色皮块数
2x-4=20
2x-20=4
2x=20+4
(20+4)÷2
=12(块)
解:设共有x块黑色皮。
解:设共有x块黑色皮。
解:设共有x块黑色皮。
等量关系:
(1)黑色皮块数×2-4=白色皮块数
2x-4=20
解:设共有x块黑色皮。
2x-4+4=20+4
2x=24
x=12
2x÷2=24÷2
先把2x看做一个整体。
答:设共有12块黑色皮。
(2)黑色皮块数×2-白色皮块数=4
(3)黑色皮块数×2=白色皮块数+4
2x-20=4
2x=20+4
解:设共有x块黑色皮。
解:设共有x块黑色皮。
同学们独立解答,看看计算结果是否一致。
检验计算结果是否正确。
x=12
x=12
1.找出未知数,用字母x表示;
小结:列方程解决实际问题的步骤
2.分析实际问题中的数量关系,找出等量关系,列方程;
3.解方程并检验作答。
三、巩固练习,学以致用
(一)基础练习
1.共有1428个网球,每5个装一筒,装完后还剩3个。一共装了多少筒?
解:设一共装了x筒。
解得 x=285
5x+3=1428
答:一共装了285筒。
每筒网球的个数×筒数+3=网球总数
2.故宫的面积是72万平方米,比天安门广场面积的2倍少16万平方米。天安门广场的面积是多少万平方米?
(二)拓展应用:配套P47
解:设天安门广场的面积是x万平方米。
解得x=44
答:天安门广场的面积是44万平方米。
天安门广场的面积×2-16=故宫的面积
2x-16=72
四、总结归纳
1.找出未知数,用字母x表示;
2.分析实际问题中的数量关系,找出等量关系,列方程;
3.解方程并检验作答。
第三课时
一、复习旧知,引入新课
只列式不计算。
22×8+25×8
商店运来苹果和梨各8筐,每筐苹果重25 kg,每筐梨重22 kg,苹果和梨共重多少千克?
或
(22+25)×8
两个式子有什么不同?
二、合作交流,探索新知
梨每千克2.8元,苹果每千克多少钱?
解:设苹果每千克x元。
x=2.4
2.8×2
答:苹果每千克2.4元。
苹果的总价+梨的总价=总价钱
2x
=
+
10.4
2x+5.6=10.4
2x+5.6-5.6=10.4-5.6
2x=4.8
2x÷2=4.8÷2
两种水果的单价和×2=总价钱
×2
=
(x+2.8)
10.4
(2.8+x)×2÷2=10.4÷2
2.8+x=5.2
2.8+x-2.8=5.2-2.8
x=2.4
看做一个整体。
怎样检验结果是否正确?
苹果的总价+梨的总价=总价钱
两种水果的单价和×2=总价钱
2×2.4+2.8×2=10.4=总价钱
(2.8+2.4)×2=10.4=总价钱
三、巩固练习,学以致用
(一)基础练习
1.
解:设儿童票每张x元。
解得 x=1.5
2x+2×4=11
答:儿童票每张1.5元。
成人票价总和+儿童票价总和=11元
《科学家》丛书有4本,《发明家》丛书有多少本?
(二)拓展应用:配套P48
解:设《发明家》丛书有x本。
解得x=3
答:《发明家》丛书有3本。
4x+2.5×4=22
我买了两套丛书,共花了22元。
2.
《科学家》丛书的总价+《发明家》丛书的总价=11元
四、总结归纳
总结:学会了解形如ax+ab=c的方程,明白乘法分配律也可以运用到解方程中,还知道有些实际问题不止一种列方程的方法。
