小学数学人教版五年级上4.1可 能 性 课件(25张ppt)
文档属性
| 名称 | 小学数学人教版五年级上4.1可 能 性 课件(25张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-13 00:00:00 | ||
图片预览






文档简介
第3单元 可 能 性
1
一、创设情境,引出课题
为了奖励A、B、C这3个考到100分的同学,老师准备了三个礼物,分别是钢笔、笔记本、尺子。为了公平起见,把这三份礼物写在纸上,三个同学进行抽签。
A同学第一个抽签,他会抽到什么礼物?
可能是钢笔,可能是笔记本,可能是尺子。
A同学抽到尺子,接下来B同学第二个抽签,他会抽到什么礼物?
可能是钢笔,可能是笔记本,不可能是尺子。
B同学抽到钢笔,接下来C同学第三个抽签,他会抽到什么礼物?
一定是笔记本。
二、动手操作,探索新知
三张卡片分别写着唱歌、跳舞、朗诵,小明可能会抽到什么节目?
可能是唱歌。
也可能是朗诵。
三种情况都有可能。
小明
小雪
小丽
我抽到了跳舞。
小明抽完还有两张。接下来小丽可能会抽到什么?
唱歌和朗诵都有可能。
不可能是跳舞。
最后只有一张了,小雪会抽到什么?
三、巩固练习,学以致用
(一)基础练习
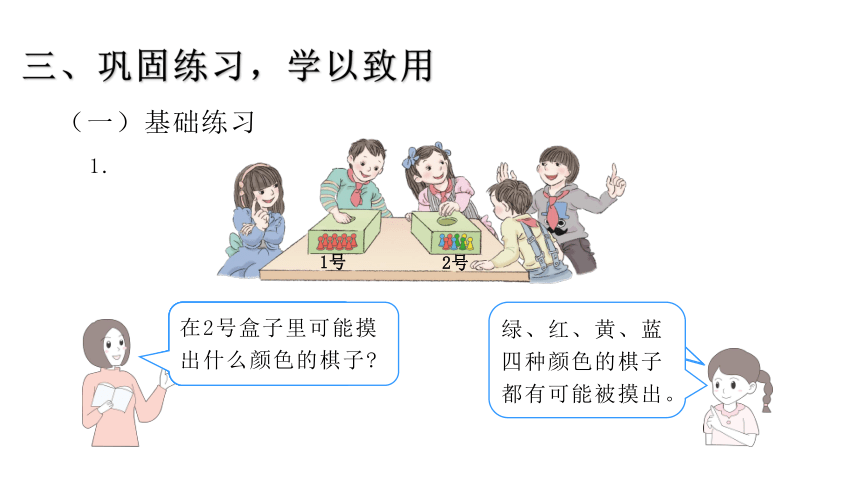
1.
哪个盒子里肯定能摸出红棋子?
1号盒子。
哪个盒子里不可能摸出绿棋子?
1号盒子。
哪个盒子里可能摸出绿棋子?
2号盒子。
在2号盒子里可能摸出什么颜色的棋子?
绿、红、黄、蓝四种颜色的棋子都有可能被摸出。
1号
2号
2.说一说指针可能停在哪种颜色上?
可能停在蓝色、粉色、绿色或黄色上。
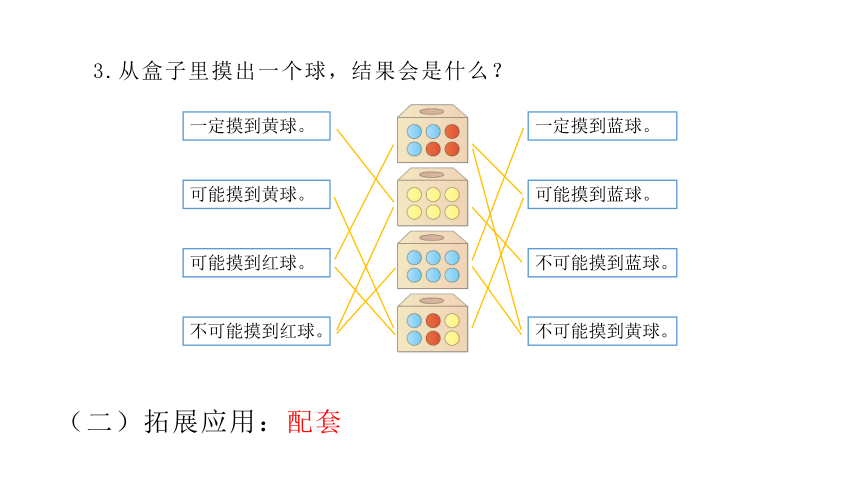
3.从盒子里摸出一个球,结果会是什么?
(二)拓展应用:配套
一定摸到黄球。
可能摸到黄球。
可能摸到红球。
不可能摸到红球。
一定摸到蓝球。
可能摸到蓝球。
不可能摸到蓝球。
不可能摸到黄球。
四、总结归纳
总结:事件发生的可能性有三种情况:“可能”“不可能”“一定”。要能结合实际情况对一些事件进行判断。
可 能 性(2)
2
一、复习旧知,引入新课
可能、不可能、一定这三种情况。
事件发生的可能性有哪些情况?
二、动手操作,探索新知
可能是红色,也可能是蓝色。
摸出一个棋子,可能是什么颜色?
摸出一个棋子,摸出哪种颜色棋子的可能性大呢?
操作:摸出一个棋子,记录它的颜色,然后放回去摇匀再摸,重复20次。
都是摸出红色棋子的次数比蓝色的次数多。
汇总各组的结果,你有什么发现?
再摸一次,摸出哪种颜色棋子的可能性大?
摸出红色棋子的可能性大。
事件发生的大小是与在总数中所占数量的多少有关,在总数中占的数量越多,发生的可能性就越大,占的数量越少,发生的可能性也就越小。
小结:可能性大小的影响因素
三、巩固练习,学以致用
(一)基础练习
1.
指针停在哪种颜色上的可能性大?
指针停在哪种颜色上的可能性小?
停在黄色上的可能性大。
停在黄色上的可能性小。
2.他闭着眼要摸出 ,在哪个箱子里更容易摸到?
第2个箱子里更容易摸到。
3.抽签游戏。
(二)拓展应用:配套P31
我最有可能表演什么节目?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}讲故事
5张
唱 歌
3张
跳 舞
1张
最有可能表演讲故事。
四、总结归纳
总结:事件发生的可能性有大有小,在总数中占的数量越多,发生的可能性就越大,占的数量越少,发生的可能性也就越小。
可 能 性(3)
3
一、创设情境,引出课题
透明的箱子里有5个白球,3个黑球。
白球或黑球。
从箱子里能摸出什么球?
摸一个球,猜猜摸出哪种颜色的球可能性大?
摸出白球的可能性大。
二、动手操作,探索新知
小组活动:盒子中装有红、黄两种颜色的球,每个小组的盒子里装的球都是一样的。从中摸出一个球后再放回去摇匀,重复20次并记录下球的颜色。
下面是八个小组的统计情况。
1组
2组
3组
4组
5组
6组
7组
8组
合计
次数
颜色
小组
15
16
5
4
12
18
15
16
14
17
123
8
2
5
4
6
3
37
1组
2组
3组
4组
5组
6组
7组
8组
合计
次数
颜色
小组
15
16
5
4
12
18
15
16
14
17
123
8
2
5
4
6
3
37
根据数据,你发现了什么规律?
都是摸出红球的次数比黄球的次数多。
盒子里是红球多还是黄球多呢?
红球多。
再摸一次,摸出哪种颜色的球可能性大?
红球。
根据摸到的结果可以反推物体的数量,摸到的次数越多,它的数量就越多;反之,摸到的次数越少,它的数量就越少。
小结:结果反推数量
三、巩固练习,学以致用
(一)基础练习
1.猜一猜,摸出哪种颜色棋子的可能性最大?摸出哪种颜色棋子的可能性最小?
摸出一个棋子,可能是什么颜色?
摸出一个棋子,可能是红色、蓝色或黄色。
盒子里红色棋子最多,所以摸出红色棋子的可能性最大。
盒子里黄色棋子最少,所以摸出黄色棋子的可能性最小。
2.掷一掷。
哪面朝上?
全班每人掷一次。
朝上的有_____人。
朝上的有_____人。
3.给 涂上红、蓝两种颜色,要使掷出红色朝上的可能性比蓝色大,应该怎么涂?
(二)拓展应用:配套P31
可以5个面涂红色,1个面涂蓝色。
还可以4个面涂红色,2个面涂蓝色。
四、总结归纳
总结:从数量的多少可以推测出事件发生可能性的大小,反过来也可以通过事件发生的次数推出数量的多少。
1
一、创设情境,引出课题
为了奖励A、B、C这3个考到100分的同学,老师准备了三个礼物,分别是钢笔、笔记本、尺子。为了公平起见,把这三份礼物写在纸上,三个同学进行抽签。
A同学第一个抽签,他会抽到什么礼物?
可能是钢笔,可能是笔记本,可能是尺子。
A同学抽到尺子,接下来B同学第二个抽签,他会抽到什么礼物?
可能是钢笔,可能是笔记本,不可能是尺子。
B同学抽到钢笔,接下来C同学第三个抽签,他会抽到什么礼物?
一定是笔记本。
二、动手操作,探索新知
三张卡片分别写着唱歌、跳舞、朗诵,小明可能会抽到什么节目?
可能是唱歌。
也可能是朗诵。
三种情况都有可能。
小明
小雪
小丽
我抽到了跳舞。
小明抽完还有两张。接下来小丽可能会抽到什么?
唱歌和朗诵都有可能。
不可能是跳舞。
最后只有一张了,小雪会抽到什么?
三、巩固练习,学以致用
(一)基础练习
1.
哪个盒子里肯定能摸出红棋子?
1号盒子。
哪个盒子里不可能摸出绿棋子?
1号盒子。
哪个盒子里可能摸出绿棋子?
2号盒子。
在2号盒子里可能摸出什么颜色的棋子?
绿、红、黄、蓝四种颜色的棋子都有可能被摸出。
1号
2号
2.说一说指针可能停在哪种颜色上?
可能停在蓝色、粉色、绿色或黄色上。
3.从盒子里摸出一个球,结果会是什么?
(二)拓展应用:配套
一定摸到黄球。
可能摸到黄球。
可能摸到红球。
不可能摸到红球。
一定摸到蓝球。
可能摸到蓝球。
不可能摸到蓝球。
不可能摸到黄球。
四、总结归纳
总结:事件发生的可能性有三种情况:“可能”“不可能”“一定”。要能结合实际情况对一些事件进行判断。
可 能 性(2)
2
一、复习旧知,引入新课
可能、不可能、一定这三种情况。
事件发生的可能性有哪些情况?
二、动手操作,探索新知
可能是红色,也可能是蓝色。
摸出一个棋子,可能是什么颜色?
摸出一个棋子,摸出哪种颜色棋子的可能性大呢?
操作:摸出一个棋子,记录它的颜色,然后放回去摇匀再摸,重复20次。
都是摸出红色棋子的次数比蓝色的次数多。
汇总各组的结果,你有什么发现?
再摸一次,摸出哪种颜色棋子的可能性大?
摸出红色棋子的可能性大。
事件发生的大小是与在总数中所占数量的多少有关,在总数中占的数量越多,发生的可能性就越大,占的数量越少,发生的可能性也就越小。
小结:可能性大小的影响因素
三、巩固练习,学以致用
(一)基础练习
1.
指针停在哪种颜色上的可能性大?
指针停在哪种颜色上的可能性小?
停在黄色上的可能性大。
停在黄色上的可能性小。
2.他闭着眼要摸出 ,在哪个箱子里更容易摸到?
第2个箱子里更容易摸到。
3.抽签游戏。
(二)拓展应用:配套P31
我最有可能表演什么节目?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}讲故事
5张
唱 歌
3张
跳 舞
1张
最有可能表演讲故事。
四、总结归纳
总结:事件发生的可能性有大有小,在总数中占的数量越多,发生的可能性就越大,占的数量越少,发生的可能性也就越小。
可 能 性(3)
3
一、创设情境,引出课题
透明的箱子里有5个白球,3个黑球。
白球或黑球。
从箱子里能摸出什么球?
摸一个球,猜猜摸出哪种颜色的球可能性大?
摸出白球的可能性大。
二、动手操作,探索新知
小组活动:盒子中装有红、黄两种颜色的球,每个小组的盒子里装的球都是一样的。从中摸出一个球后再放回去摇匀,重复20次并记录下球的颜色。
下面是八个小组的统计情况。
1组
2组
3组
4组
5组
6组
7组
8组
合计
次数
颜色
小组
15
16
5
4
12
18
15
16
14
17
123
8
2
5
4
6
3
37
1组
2组
3组
4组
5组
6组
7组
8组
合计
次数
颜色
小组
15
16
5
4
12
18
15
16
14
17
123
8
2
5
4
6
3
37
根据数据,你发现了什么规律?
都是摸出红球的次数比黄球的次数多。
盒子里是红球多还是黄球多呢?
红球多。
再摸一次,摸出哪种颜色的球可能性大?
红球。
根据摸到的结果可以反推物体的数量,摸到的次数越多,它的数量就越多;反之,摸到的次数越少,它的数量就越少。
小结:结果反推数量
三、巩固练习,学以致用
(一)基础练习
1.猜一猜,摸出哪种颜色棋子的可能性最大?摸出哪种颜色棋子的可能性最小?
摸出一个棋子,可能是什么颜色?
摸出一个棋子,可能是红色、蓝色或黄色。
盒子里红色棋子最多,所以摸出红色棋子的可能性最大。
盒子里黄色棋子最少,所以摸出黄色棋子的可能性最小。
2.掷一掷。
哪面朝上?
全班每人掷一次。
朝上的有_____人。
朝上的有_____人。
3.给 涂上红、蓝两种颜色,要使掷出红色朝上的可能性比蓝色大,应该怎么涂?
(二)拓展应用:配套P31
可以5个面涂红色,1个面涂蓝色。
还可以4个面涂红色,2个面涂蓝色。
四、总结归纳
总结:从数量的多少可以推测出事件发生可能性的大小,反过来也可以通过事件发生的次数推出数量的多少。
