人教A版数学高三数学一轮复习第一章第二节 命题及其关系、充分条件与必要条件
文档属性
| 名称 | 人教A版数学高三数学一轮复习第一章第二节 命题及其关系、充分条件与必要条件 |

|
|
| 格式 | zip | ||
| 文件大小 | 425.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-06-02 00:00:00 | ||
图片预览











文档简介
(共33张PPT)
第二节 命题及其关系、充分条件与必要条件
1.命题的概念
在数学中用语言、符号或式子表达的,可以 的陈述句叫做命题.其
中 的语句叫真命题, 的语句叫假命题.
2.四种命题及其关系
(1)四种命题
判断真假
判断为真
判断为假
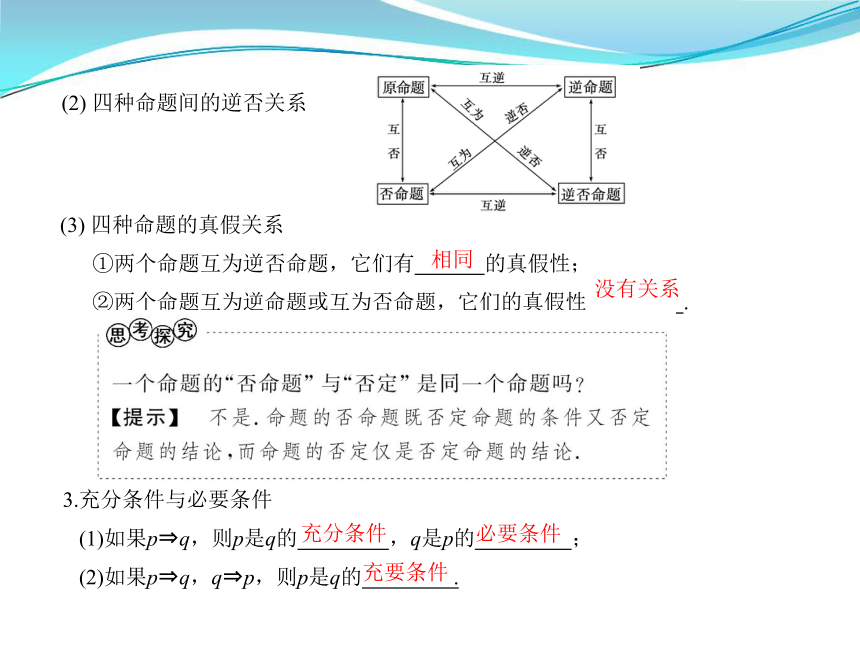
(2) 四种命题间的逆否关系
(3) 四种命题的真假关系
①两个命题互为逆否命题,它们有 的真假性;
②两个命题互为逆命题或互为否命题,它们的真假性 .
相同
没有关系
3.充分条件与必要条件
(1)如果p q,则p是q的 ,q是p的 ;
(2)如果p q,q p,则p是q的 .
充分条件
必要条件
充要条件
1.(2012年湖南模拟,2)设集合M={1,2},N={a2},则“a=1”是“N M”
的 ( )
A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分又不必要条件
【解析】 显然a=1时一定有N M,反之则不一定成立,如a=-1.故是充分
不必要条件.
【答案】 A
2.命题“若x=1或x=6,则(x-1)(x-6)=0”的逆否命题是4 ( )
A.若x≠1或x≠6,则(x-1)(x-6)≠0
B.若x≠1且x≠6,则(x-1)(x-6)≠0
C.若(x-1)(x-6)≠0,则x≠1或x≠6
D.若(x-1)(x-6)≠0,则x≠1且x≠6
【解析】 首先根据命题“若p则q”的逆否命题为“若綈q则綈p”,排除A、
B,再根据命题“p且q”的否定是“綈p或綈q”,命题“p或q”的否定是“綈p
且綈q”,可知C错误,D正确.
【答案】 D
3.已知命题“若函数f(x)=ex-mx在(0,+∞)上是增函数,则m≤1”,则下列结
论正确的是 ( )
A.否命题是“若函数f(x)=ex-mx在(0,+∞)上是减函数,则m>1”,是真
命题
B.逆命题是“若m≤1,则函数f(x)=ex-mx在(0,+∞)上是增函数”,是假
命题
C.逆否命题是“若m>1,则函数f(x)=ex-mx在(0,+∞)上是减函数”,是
真命题
D.逆否命题是“若m>1,则函数f(x)=ex-mx在(0,+∞)上不是增函数”,
是真命题
【解析】 f′(x)=ex-m≥0在(0+∞)上恒成立,即m≤ex在(0,+∞)上恒成立,
故m≤1,这说明原命题正确,反之若m≤1,则f′(x)>0在(0,+∞)上恒成立 ,故
逆命题正确,但对增函数的否定不是减函数,而是“不是增函数”,故选D.
【答案】 D
4.i、j是不共线的单位向量,若a=5i+3j,b=3i-5j,则a⊥b的充要条件是________.
【解析】 a⊥b a·b=0,即(5i+3j)·(3i-5j)=0,
即15i2-16i·j-15j2=0,
∵|i|=|j|=1,∴16i·j=0,即i·j=0,∴i⊥j.
【答案】 i⊥j
5.“若a≤b,则ac2≤bc2.”则命题的原命题、逆命题、否命题和逆否命题中正确命
题的个数是________.
【解析】 其中原命题和逆否命题为真命题,逆命题和否命题为假命题.
【答案】 2
考点一 命题的关系及真假的判断
1.命题真假的判定
对于命题真假的判定,关键是分清命题的条件与结论,只有将条件与结论分
清,再结合所涉及的知识才能正确地判断命题的真假.
2.四种命题的关系的应用
掌握原命题和逆否命题,否命题和逆命题的等价性,当一个命题直接判断它
的真假不易进行时,可以转而判断其逆否命题的真假.
【特别提醒】 当一个命题有大前提而写出其他三种命题时,必须保留大前提,
大前提不动.
分别写出下列命题的逆命题、否命题、逆否命题、命题的否定,并
判断它们的真假:
(1)若q≤1,则方程x2+2x+q=0有实根;
(2)若x、y都是奇数,则x+y是偶数;
(3)若xy=0,则x=0或y=0;
(4)若x2+y2=0,则x、y全为0.
【思路点拨】
【自主解答】 (1)原命题是真命题;
逆命题:若方程x2+2x+q=0有实根,则q≤1,为真命题;
否命题:若q>1,则方程x2+2x+q=0无实根,为真命题;
逆否命题:若方程x2+2x+q=0无实根,则q>1,为真命题;
命题的否定:若q≤1,则方程x2+2x+q=0无实根,为假命题.
(2)原命题是真命题;
逆命题:若x+y是偶数,则x、y都是奇数,是假命题;
否命题:若x、y不都是奇数,则x+y不是偶数,是假命题;
逆否命题:若x+y不是偶数,则x、y不都是奇数,是真命题;
命题的否定:若x、y都是奇数,则x+y不是偶数,是假命题.
(3)原命题为真命题;
逆命题:若x=0或y=0,则xy=0,是真命题;
否命题:若xy≠0,则x≠0且y≠0,是真命题;
逆否命题:若x≠0且y≠0,则xy≠0,是真命题;
命题的否定:若xy=0,则x≠0且y≠0,是假命题.
(4)原命题为真命题.
逆命题:若x、y全为0,则x2+y2=0,为真命题;
否命题:若x2+y2≠0,则x、y不全为0,为真命题;
逆否命题:若x、y不全为0,则x2+y2≠0,为真命题;
命题的否定:若x2+y2=0,则x、y不全为0,是假命题.
1.有下列四个命题:
①“若xy=1,则x,y互为倒数”的逆命题;
②“相似三角形的周长相等”的否命题;
③“若b≤-1,则方程x2-2bx+b2+b=0有实根”的逆否命题;
④“若A∪B=B,则A B”的逆否命题.
其中真命题的序号是________.
【解析】 ①的逆命题为:若x,y互为倒数,则xy=1,是真命题;②的否命
题:不相似的三角形的周长不相等,是假命题;对③,若方程x2-2bx+b2+b=0
有实根,则Δ=4b2-4(b2+b)≥0,∴b≤0,故命题“若b≤-1,则方程x2-2bx+
b2+b=0有实根”是真命题,其逆否命题也为真命题.对④,∵若A∪B=B,则
A B, ∴命题“若A∪B=B,则A B”是假命题,其逆否命题也是假命题.
【答案】 ①③
考点二 充要条件的判定
判断一个命题是另一个命题的什么条件,关键是利用定义:如果p q,则
p叫做q的充分条件,原命题(或逆否命题)成立,命题中的条件是充分的,也可
称q是p的必要条件;如果q p,则p叫做q的必要条件,逆命题(或否命题)成立,
命题中的条件为必要的,也可称q是p的充分条件;如果既有p q,又有q p,
则p叫做q的充分必要条件,简称充要条件,记作p q,原命题和逆命题(或逆否
命题和否命题)都成立,命题中的条件是充要的.
【特别提醒】 从集合的角度理解,小范围可以推出大范围,大范围不能推
出小范围.
指出下列各组命题中,p是q的什么条件?
(1)p:a+b=2,
q:直线x+y=0与圆(x-a)2+(y-b)2=2相切;
(2)p:|x|=x,q:x2+x≥0;
(3)设l,m均为直线,α为平面,其中l α,m α,p:l∥α,q:l∥m;
考点三 利用充分条件与必要条件求参数的取值范围
解决此类问题一般是把充分条件、必要条件或充要条件转化为集合之间的
关系,然后根据集合之间的关系列出关于参数的不等式求解.
【思路点拨】 可以直接求綈p、綈q的命题转化为集合运算,也可以利用綈
p 綈q的逆否命题再转化为集合运算.
3.设命题p:(4x-3)2≤1;命题q:x2-(2a+1)x+a(a+1)≤0,若綈p是綈q的必
要不充分条件,求实数a的取值范围.
一、选择题
1.给出命题:若函数y=f(x)是幂函数,则函数y=f(x)的图象不过第四象限.在
它的逆命题、否命题、逆否命题三个命题中,真命题的个数是 ( )
A.3 B.2
C.1 D.0
【解析】 原命题与逆否命题等价,而原命题为真,所以逆否命题为真命题.
原命题的逆命题为:若y=f(x)的图象不过第四象限,则函数y=f(x)是幂函数,显
然此命题为假.又因为逆命题与否命题同真假,所以否命题为假.故选C.
【答案】 C
2.若命题p的否命题为r,命题r的逆命题为s,则s是p的 ( )
A.逆否命题 B.逆命题
C.否命题 D.原命题
【解析】 由四种命题的逆否关系知,s是p的逆否命题.
【答案】 A
3.(2012年天津模拟,4)设集合A={x∈R|x-2>0},B={x∈R|x<0},C=
{x∈R|x(x-2)>0},则“x∈A∪B”是“x∈C”的 ( )
A.充分而不必要条件
B.必要而不充分条件
C.充分必要条件
D.既不充分也不必要条件
【解析】 A∪B={x∈R|x<0或x>2},C={x∈R|x<0或x>2},∵A∪B=C,
∴x∈A∪B是x∈C的充分必要条件.故选C.
【答案】 C
4.下列选项中,p是q的必要不充分条件的是 ( )
A.p:a+c>b+d,q:a>b且c>d
B.p:a>1,b>1,q:f(x)=ax-b(a>0,且a≠1)的图象不过第二象限
C.p:x=1,q:x2=x
D.p:a>1,q:f(x)=logax(a>0,且a≠1)在(0,+∞)上为增函数
【解析】 由于a>b,c>d a+c>b+d,而a+c>b+d却不一定推出a>b,
c>d.故A中p是q的必要不充分条件.B中,当a>1,b>1时,函数f(x)=ax-b不
过第二象限,当f(x)=ax-b不过第二象限时,有a>1,b≥1.故B中p是q的充分不
必要条件.C中,因为x=1时有x2=x,但x2=x时不一定有x=1,故C中p是q的充
分不必要条件.D中p是q的充要条件.
【答案】 A
5.已知条件p:(x+1)2>4,条件q:x>a,且綈p是綈q的充分而不必要条件,
则a的取值范围是 ( )
A.a≥1 B.a≤1
C.a≥-3 D.a≤-3
【解析】 由(x+1)2>4得x>1或x<-3,∴p:x>1或x<-3,∵綈p是綈q
的充分而不必要条件,即p是q的必要不充分条件,∴p /q,但q p,∴a≥1.
【答案】 A
二、填空题
6.已知直线l1:x+ay+6=0和l2:(a-2)x+3y+2a=0,则l1∥l2的充要条件是a
=________.
【解析】 由1×3-a×(a-2)=0得a=3或-1,而a=3时,两条直线重合,
所以a=-1.
【答案】 -1
7.给定下列命题:
①若k>0,则方程x2+2x-k=0有实数根;
②若x+y≠8,则x≠2或y≠6;
③“矩形的对角线相等”的逆命题;
④“若xy=0,则x、y中至少有一个为0”的否命题.
其中真命题的序号是________.
【解析】 ①∵Δ=4-4(-k)=4+4k>0,∴①是真命题.②其逆否命题为真,
故②是真命题.③逆命题:“对角线相等的四边形是矩形”是假命题.④否命题:
“若xy≠0,则x、y都不为零”是真命题.
【答案】 ①②④
三、解答题
8.设计如下四个电路图,条件A:“开关A闭合”,条件B:“灯泡B亮”,问A
是B的什么条件?
【解析】 图(1)中开关A闭合则灯泡B亮,反之,灯泡B亮不一定有开关A闭合.
∴A B,但B /A,于是A是B的充分非必要条件.
图(2)中,A B,A是B的充要条件.
图(3)中,A /B,但B A,A是B的必要非充分条件.
图(4)中,条件A的有无对条件B没有影响,所以A是B的既不充分又不必要条件.
9.已知函数f(x)是(-∞,+∞)上的增函数,a、b∈R,对命题“若a+b≥0,
则f(a)+f(b)≥f(-a)+f(-b)”.
(1)写出其逆命题,判断其真假,并证明你的结论;
(2)写出其逆否命题,判断其真假,并证明你的结论.
【解析】 (1)逆命题是:若f(a)+f(b)≥f(-a)+f(-b),
则a+b≥0为真命题.
用反证法证明:假设a+b<0,则a<-b,b<-a.
∵f(x)是(-∞,+∞)上的增函数,
则f(a)<f(-b),f(b)<f(-a),
∴f(a)+f(b)<f(-a)+f(-b),这与题设相矛盾,所以逆命题为真.
(2)逆否命题:若f(a)+f(b)<f(-a)+f(-b),
则a+b<0为真命题.
因为原命题 它的逆否命题,所以证明原命题为真命题即可.
∵a+b≥0,∴a≥-b,b≥-a.
又∵f(x)在(-∞,+∞)上是增函数,
∴f(a)≥f(-b),f(b)≥f(-a),
∴f(a)+f(b)≥f(-a)+f(-b).
所以逆否命题为真.
【答案】 B
从近两年的高考试题看,充要条件的判定、命题真假的判断等是高考的热
点,题型以选择题、填空题为主,分值为5分,属中低档题目.本节知识常和函
数、不等式、向量、三角函数及立体几何中直线、平面的位置关系等有关知识
相结合,考查学生对函数的有关性质、不等式的解法及直线与平面位置关系判
定的掌握程度.
预测2013年高考仍将以充要条件的判定、判断命题的真假为主要考点,重点
考查学生的逻辑推理能力.
【答案】 A
【答案】 D
【方法指导】 1.当一个命题有大前提而要写出其它三种命题时,必须保留大
前提,也就是大前提不动;对于由多个并列条件组成的命题,在写其它三种命题
时,应把其中一个(或n个)作为大前提.
2.数学中的定义、公理、公式、定理都是命题,但命题与定理是有区别的;命题
有真假之分,而定理都是真的.
3.命题的充要关系的判断方法
(1)定义法:直接判断若p则q、若q则p的真假.
(2)等价法:利用A B与 B A,B A与 A B,A B与 B A的等价关系,
对于条件或结论是否定式的命题,一般运用等价法.
(3)利用集合间的包含关系判断:若A B,则A是B的充分条件或B是A的必要条件;
若A=B,则A是B的充要条件.
【解析】 只需将原命题的结论变为新命题的条件,同时将原命题的条件变成新
命题的结论既可,即“若|a|=|b|,则a=-b”.
【答案】 D
2.(2012年福建调研)若a∈R,则“a=2”是“(a-1)(a-2)=0”的 ( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分又不必要条件
【解析】 由a=2能得到(a-1)(a-2)=0,但由(a-1)(a-2)=0得到a=1或a=2,
而不是a=2,所以a=2是(a-1)(a-2)=0的充分不必要条件.
【答案】 A
(文)(2011年高考福建卷)若a∈R,则“a=1”是“|a|=1”的 ( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分又不必要条件
【解析】 若a=1,则|a|=1是真命题,即a=1 |a|=1,由|a|=1可得a=±1,所
以若|a|=1,则有a=1是假命题,即|a|=1 a=1不成立,所以a=1是|a|=1的充分而
不必要条件,故选A.
【答案】 A
【答案】 B
第二节 命题及其关系、充分条件与必要条件
1.命题的概念
在数学中用语言、符号或式子表达的,可以 的陈述句叫做命题.其
中 的语句叫真命题, 的语句叫假命题.
2.四种命题及其关系
(1)四种命题
判断真假
判断为真
判断为假
(2) 四种命题间的逆否关系
(3) 四种命题的真假关系
①两个命题互为逆否命题,它们有 的真假性;
②两个命题互为逆命题或互为否命题,它们的真假性 .
相同
没有关系
3.充分条件与必要条件
(1)如果p q,则p是q的 ,q是p的 ;
(2)如果p q,q p,则p是q的 .
充分条件
必要条件
充要条件
1.(2012年湖南模拟,2)设集合M={1,2},N={a2},则“a=1”是“N M”
的 ( )
A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分又不必要条件
【解析】 显然a=1时一定有N M,反之则不一定成立,如a=-1.故是充分
不必要条件.
【答案】 A
2.命题“若x=1或x=6,则(x-1)(x-6)=0”的逆否命题是4 ( )
A.若x≠1或x≠6,则(x-1)(x-6)≠0
B.若x≠1且x≠6,则(x-1)(x-6)≠0
C.若(x-1)(x-6)≠0,则x≠1或x≠6
D.若(x-1)(x-6)≠0,则x≠1且x≠6
【解析】 首先根据命题“若p则q”的逆否命题为“若綈q则綈p”,排除A、
B,再根据命题“p且q”的否定是“綈p或綈q”,命题“p或q”的否定是“綈p
且綈q”,可知C错误,D正确.
【答案】 D
3.已知命题“若函数f(x)=ex-mx在(0,+∞)上是增函数,则m≤1”,则下列结
论正确的是 ( )
A.否命题是“若函数f(x)=ex-mx在(0,+∞)上是减函数,则m>1”,是真
命题
B.逆命题是“若m≤1,则函数f(x)=ex-mx在(0,+∞)上是增函数”,是假
命题
C.逆否命题是“若m>1,则函数f(x)=ex-mx在(0,+∞)上是减函数”,是
真命题
D.逆否命题是“若m>1,则函数f(x)=ex-mx在(0,+∞)上不是增函数”,
是真命题
【解析】 f′(x)=ex-m≥0在(0+∞)上恒成立,即m≤ex在(0,+∞)上恒成立,
故m≤1,这说明原命题正确,反之若m≤1,则f′(x)>0在(0,+∞)上恒成立 ,故
逆命题正确,但对增函数的否定不是减函数,而是“不是增函数”,故选D.
【答案】 D
4.i、j是不共线的单位向量,若a=5i+3j,b=3i-5j,则a⊥b的充要条件是________.
【解析】 a⊥b a·b=0,即(5i+3j)·(3i-5j)=0,
即15i2-16i·j-15j2=0,
∵|i|=|j|=1,∴16i·j=0,即i·j=0,∴i⊥j.
【答案】 i⊥j
5.“若a≤b,则ac2≤bc2.”则命题的原命题、逆命题、否命题和逆否命题中正确命
题的个数是________.
【解析】 其中原命题和逆否命题为真命题,逆命题和否命题为假命题.
【答案】 2
考点一 命题的关系及真假的判断
1.命题真假的判定
对于命题真假的判定,关键是分清命题的条件与结论,只有将条件与结论分
清,再结合所涉及的知识才能正确地判断命题的真假.
2.四种命题的关系的应用
掌握原命题和逆否命题,否命题和逆命题的等价性,当一个命题直接判断它
的真假不易进行时,可以转而判断其逆否命题的真假.
【特别提醒】 当一个命题有大前提而写出其他三种命题时,必须保留大前提,
大前提不动.
分别写出下列命题的逆命题、否命题、逆否命题、命题的否定,并
判断它们的真假:
(1)若q≤1,则方程x2+2x+q=0有实根;
(2)若x、y都是奇数,则x+y是偶数;
(3)若xy=0,则x=0或y=0;
(4)若x2+y2=0,则x、y全为0.
【思路点拨】
【自主解答】 (1)原命题是真命题;
逆命题:若方程x2+2x+q=0有实根,则q≤1,为真命题;
否命题:若q>1,则方程x2+2x+q=0无实根,为真命题;
逆否命题:若方程x2+2x+q=0无实根,则q>1,为真命题;
命题的否定:若q≤1,则方程x2+2x+q=0无实根,为假命题.
(2)原命题是真命题;
逆命题:若x+y是偶数,则x、y都是奇数,是假命题;
否命题:若x、y不都是奇数,则x+y不是偶数,是假命题;
逆否命题:若x+y不是偶数,则x、y不都是奇数,是真命题;
命题的否定:若x、y都是奇数,则x+y不是偶数,是假命题.
(3)原命题为真命题;
逆命题:若x=0或y=0,则xy=0,是真命题;
否命题:若xy≠0,则x≠0且y≠0,是真命题;
逆否命题:若x≠0且y≠0,则xy≠0,是真命题;
命题的否定:若xy=0,则x≠0且y≠0,是假命题.
(4)原命题为真命题.
逆命题:若x、y全为0,则x2+y2=0,为真命题;
否命题:若x2+y2≠0,则x、y不全为0,为真命题;
逆否命题:若x、y不全为0,则x2+y2≠0,为真命题;
命题的否定:若x2+y2=0,则x、y不全为0,是假命题.
1.有下列四个命题:
①“若xy=1,则x,y互为倒数”的逆命题;
②“相似三角形的周长相等”的否命题;
③“若b≤-1,则方程x2-2bx+b2+b=0有实根”的逆否命题;
④“若A∪B=B,则A B”的逆否命题.
其中真命题的序号是________.
【解析】 ①的逆命题为:若x,y互为倒数,则xy=1,是真命题;②的否命
题:不相似的三角形的周长不相等,是假命题;对③,若方程x2-2bx+b2+b=0
有实根,则Δ=4b2-4(b2+b)≥0,∴b≤0,故命题“若b≤-1,则方程x2-2bx+
b2+b=0有实根”是真命题,其逆否命题也为真命题.对④,∵若A∪B=B,则
A B, ∴命题“若A∪B=B,则A B”是假命题,其逆否命题也是假命题.
【答案】 ①③
考点二 充要条件的判定
判断一个命题是另一个命题的什么条件,关键是利用定义:如果p q,则
p叫做q的充分条件,原命题(或逆否命题)成立,命题中的条件是充分的,也可
称q是p的必要条件;如果q p,则p叫做q的必要条件,逆命题(或否命题)成立,
命题中的条件为必要的,也可称q是p的充分条件;如果既有p q,又有q p,
则p叫做q的充分必要条件,简称充要条件,记作p q,原命题和逆命题(或逆否
命题和否命题)都成立,命题中的条件是充要的.
【特别提醒】 从集合的角度理解,小范围可以推出大范围,大范围不能推
出小范围.
指出下列各组命题中,p是q的什么条件?
(1)p:a+b=2,
q:直线x+y=0与圆(x-a)2+(y-b)2=2相切;
(2)p:|x|=x,q:x2+x≥0;
(3)设l,m均为直线,α为平面,其中l α,m α,p:l∥α,q:l∥m;
考点三 利用充分条件与必要条件求参数的取值范围
解决此类问题一般是把充分条件、必要条件或充要条件转化为集合之间的
关系,然后根据集合之间的关系列出关于参数的不等式求解.
【思路点拨】 可以直接求綈p、綈q的命题转化为集合运算,也可以利用綈
p 綈q的逆否命题再转化为集合运算.
3.设命题p:(4x-3)2≤1;命题q:x2-(2a+1)x+a(a+1)≤0,若綈p是綈q的必
要不充分条件,求实数a的取值范围.
一、选择题
1.给出命题:若函数y=f(x)是幂函数,则函数y=f(x)的图象不过第四象限.在
它的逆命题、否命题、逆否命题三个命题中,真命题的个数是 ( )
A.3 B.2
C.1 D.0
【解析】 原命题与逆否命题等价,而原命题为真,所以逆否命题为真命题.
原命题的逆命题为:若y=f(x)的图象不过第四象限,则函数y=f(x)是幂函数,显
然此命题为假.又因为逆命题与否命题同真假,所以否命题为假.故选C.
【答案】 C
2.若命题p的否命题为r,命题r的逆命题为s,则s是p的 ( )
A.逆否命题 B.逆命题
C.否命题 D.原命题
【解析】 由四种命题的逆否关系知,s是p的逆否命题.
【答案】 A
3.(2012年天津模拟,4)设集合A={x∈R|x-2>0},B={x∈R|x<0},C=
{x∈R|x(x-2)>0},则“x∈A∪B”是“x∈C”的 ( )
A.充分而不必要条件
B.必要而不充分条件
C.充分必要条件
D.既不充分也不必要条件
【解析】 A∪B={x∈R|x<0或x>2},C={x∈R|x<0或x>2},∵A∪B=C,
∴x∈A∪B是x∈C的充分必要条件.故选C.
【答案】 C
4.下列选项中,p是q的必要不充分条件的是 ( )
A.p:a+c>b+d,q:a>b且c>d
B.p:a>1,b>1,q:f(x)=ax-b(a>0,且a≠1)的图象不过第二象限
C.p:x=1,q:x2=x
D.p:a>1,q:f(x)=logax(a>0,且a≠1)在(0,+∞)上为增函数
【解析】 由于a>b,c>d a+c>b+d,而a+c>b+d却不一定推出a>b,
c>d.故A中p是q的必要不充分条件.B中,当a>1,b>1时,函数f(x)=ax-b不
过第二象限,当f(x)=ax-b不过第二象限时,有a>1,b≥1.故B中p是q的充分不
必要条件.C中,因为x=1时有x2=x,但x2=x时不一定有x=1,故C中p是q的充
分不必要条件.D中p是q的充要条件.
【答案】 A
5.已知条件p:(x+1)2>4,条件q:x>a,且綈p是綈q的充分而不必要条件,
则a的取值范围是 ( )
A.a≥1 B.a≤1
C.a≥-3 D.a≤-3
【解析】 由(x+1)2>4得x>1或x<-3,∴p:x>1或x<-3,∵綈p是綈q
的充分而不必要条件,即p是q的必要不充分条件,∴p /q,但q p,∴a≥1.
【答案】 A
二、填空题
6.已知直线l1:x+ay+6=0和l2:(a-2)x+3y+2a=0,则l1∥l2的充要条件是a
=________.
【解析】 由1×3-a×(a-2)=0得a=3或-1,而a=3时,两条直线重合,
所以a=-1.
【答案】 -1
7.给定下列命题:
①若k>0,则方程x2+2x-k=0有实数根;
②若x+y≠8,则x≠2或y≠6;
③“矩形的对角线相等”的逆命题;
④“若xy=0,则x、y中至少有一个为0”的否命题.
其中真命题的序号是________.
【解析】 ①∵Δ=4-4(-k)=4+4k>0,∴①是真命题.②其逆否命题为真,
故②是真命题.③逆命题:“对角线相等的四边形是矩形”是假命题.④否命题:
“若xy≠0,则x、y都不为零”是真命题.
【答案】 ①②④
三、解答题
8.设计如下四个电路图,条件A:“开关A闭合”,条件B:“灯泡B亮”,问A
是B的什么条件?
【解析】 图(1)中开关A闭合则灯泡B亮,反之,灯泡B亮不一定有开关A闭合.
∴A B,但B /A,于是A是B的充分非必要条件.
图(2)中,A B,A是B的充要条件.
图(3)中,A /B,但B A,A是B的必要非充分条件.
图(4)中,条件A的有无对条件B没有影响,所以A是B的既不充分又不必要条件.
9.已知函数f(x)是(-∞,+∞)上的增函数,a、b∈R,对命题“若a+b≥0,
则f(a)+f(b)≥f(-a)+f(-b)”.
(1)写出其逆命题,判断其真假,并证明你的结论;
(2)写出其逆否命题,判断其真假,并证明你的结论.
【解析】 (1)逆命题是:若f(a)+f(b)≥f(-a)+f(-b),
则a+b≥0为真命题.
用反证法证明:假设a+b<0,则a<-b,b<-a.
∵f(x)是(-∞,+∞)上的增函数,
则f(a)<f(-b),f(b)<f(-a),
∴f(a)+f(b)<f(-a)+f(-b),这与题设相矛盾,所以逆命题为真.
(2)逆否命题:若f(a)+f(b)<f(-a)+f(-b),
则a+b<0为真命题.
因为原命题 它的逆否命题,所以证明原命题为真命题即可.
∵a+b≥0,∴a≥-b,b≥-a.
又∵f(x)在(-∞,+∞)上是增函数,
∴f(a)≥f(-b),f(b)≥f(-a),
∴f(a)+f(b)≥f(-a)+f(-b).
所以逆否命题为真.
【答案】 B
从近两年的高考试题看,充要条件的判定、命题真假的判断等是高考的热
点,题型以选择题、填空题为主,分值为5分,属中低档题目.本节知识常和函
数、不等式、向量、三角函数及立体几何中直线、平面的位置关系等有关知识
相结合,考查学生对函数的有关性质、不等式的解法及直线与平面位置关系判
定的掌握程度.
预测2013年高考仍将以充要条件的判定、判断命题的真假为主要考点,重点
考查学生的逻辑推理能力.
【答案】 A
【答案】 D
【方法指导】 1.当一个命题有大前提而要写出其它三种命题时,必须保留大
前提,也就是大前提不动;对于由多个并列条件组成的命题,在写其它三种命题
时,应把其中一个(或n个)作为大前提.
2.数学中的定义、公理、公式、定理都是命题,但命题与定理是有区别的;命题
有真假之分,而定理都是真的.
3.命题的充要关系的判断方法
(1)定义法:直接判断若p则q、若q则p的真假.
(2)等价法:利用A B与 B A,B A与 A B,A B与 B A的等价关系,
对于条件或结论是否定式的命题,一般运用等价法.
(3)利用集合间的包含关系判断:若A B,则A是B的充分条件或B是A的必要条件;
若A=B,则A是B的充要条件.
【解析】 只需将原命题的结论变为新命题的条件,同时将原命题的条件变成新
命题的结论既可,即“若|a|=|b|,则a=-b”.
【答案】 D
2.(2012年福建调研)若a∈R,则“a=2”是“(a-1)(a-2)=0”的 ( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分又不必要条件
【解析】 由a=2能得到(a-1)(a-2)=0,但由(a-1)(a-2)=0得到a=1或a=2,
而不是a=2,所以a=2是(a-1)(a-2)=0的充分不必要条件.
【答案】 A
(文)(2011年高考福建卷)若a∈R,则“a=1”是“|a|=1”的 ( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分又不必要条件
【解析】 若a=1,则|a|=1是真命题,即a=1 |a|=1,由|a|=1可得a=±1,所
以若|a|=1,则有a=1是假命题,即|a|=1 a=1不成立,所以a=1是|a|=1的充分而
不必要条件,故选A.
【答案】 A
【答案】 B
同课章节目录
