4.1 图形的平移同步练习(含答案)
图片预览



文档简介
中小学教育资源及组卷应用平台
第四章 图形的平移与旋转
1 图形的平移
知识能力全练
知识点一 平移的定义
1.下列现象中,属于平移的是( )
①小朋友在荡秋千; ②打气筒打气时,活塞的运动; ③风车的转动;
④瓶装饮料在传送带上移动.
A.①② B.①③ C.②③ D.②④
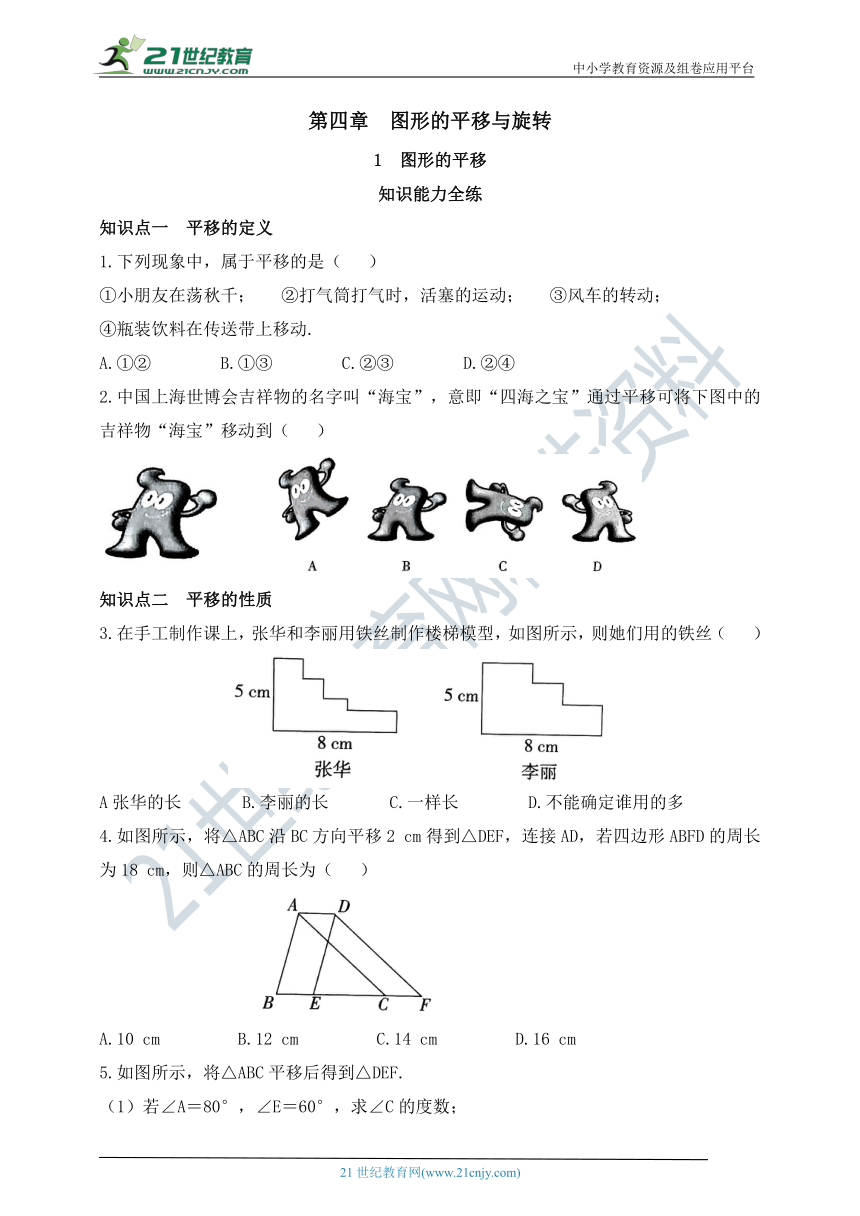
2.中国上海世博会吉祥物的名字叫“海宝”,意即“四海之宝”通过平移可将下图中的吉祥物“海宝”移动到( )
知识点二 平移的性质
3.在手工制作课上,张华和李丽用铁丝制作楼梯模型,如图所示,则她们用的铁丝( )
A张华的长 B.李丽的长 C.一样长 D.不能确定谁用的多
4.如图所示,将△ABC沿BC方向平移2 cm得到△DEF,连接AD,若四边形ABFD的周长为18 cm,则△ABC的周长为( )
A.10 cm B.12 cm C.14 cm D.16 cm
5.如图所示,将△ABC平移后得到△DEF.
(1)若∠A=80°,∠E=60°,求∠C的度数;
(2)若AC=BC,BC与DF相交于点O,则OD与OB相等吗?说明理由.
6.如图所示,将Rt△ABC沿AB方向平移得到Rt△DEF,已知BE=6,FE=10,CG=3,求阴影部分的面积.
知识点三 平移作图的一般步骤
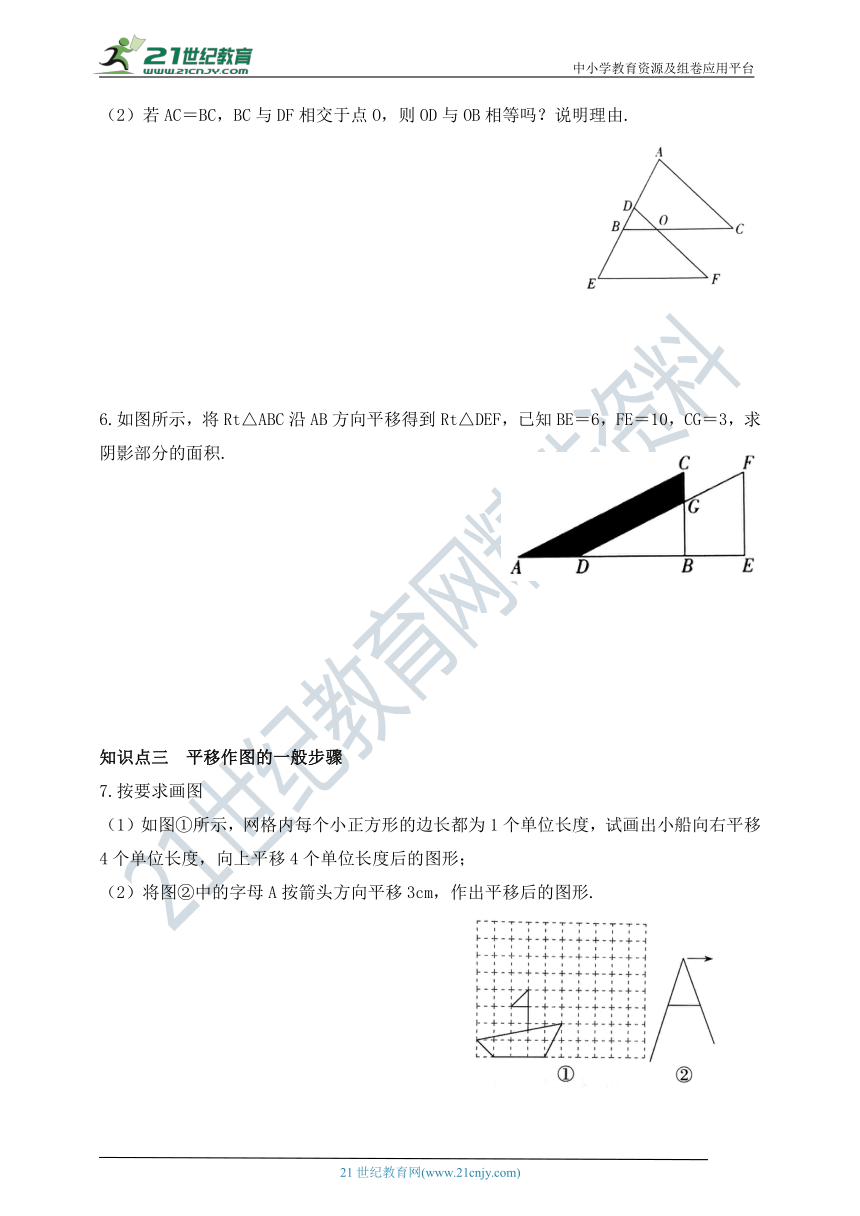
7.按要求画图
(1)如图①所示,网格内每个小正方形的边长都为1个单位长度,试画出小船向右平移4个单位长度,向上平移4个单位长度后的图形;
(2)将图②中的字母A按箭头方向平移3cm,作出平移后的图形.
8.如图所示,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点A、B、C及点A1在网格的格点上,平移后点A的对应点为A1.
(1)在网格中画出△ABC平移后所得的△A1B1C1;
(2)计算线段AC在平移到线段A1C1的过程中,扫过的区域的面积.
知识点四 图形的坐标变换与平移
9.将三角形三个顶点的横坐标都减2,纵坐标不变,则所得三角形与原三角形的关系是( )
A.将原图向左平移两个单位 B.关于原点对称
C.将原图向右平移两个单位 D.关于y轴对称
10.如图所示,在平面直角坐标系xOy中,将四边形ABCD先向下平移,再向右平移,得到四边形A1B1C1D1,已知A(-3,5),B(-4,3),A1(3,3),则B1的坐标为( )
A.(1,2) B.(2,1) C.(1,4) D.(4,1)
11.在平面直角坐标系中,点P(a-4,b+8)先向右平移3个单位长度,再向下平移6个单位长度后落在第四象限内,则点(a,b)在第________象限.
12.如图所示,在平面直角坐标系中,点A的坐标为(0,4),△OAB沿x轴向右平移后得到△O′A'B′,点A的对应点A′是直线y=上的一点,则点B与其对应点B′间的距离为___________.
13.如图所示,三角形A′B'C′是由三角形ABC平移得到的.
(1)若点P(a,b)是三角形ABC内部一点,求平移后三角形A'B'C′内的对应点P′的坐标;
(2)画出将三角形ABC向左平移4个单位,向下平移1个单位得到的三角形A1B1C1.
知识点五 图形的平移变换
14.将点A(-2,3)通过以下哪种方式的平移,可以得到点A′(-5,7)( )
A.沿x轴向右平移3个单位长度,沿y轴向上平移4个单位长度
B沿x轴向左平移3个单位长度,沿y轴向下平移4个单位长度
C.沿x轴向左平移4个单位长度,沿y轴向上平移3个单位长度
D.沿x轴向左平移3个单位长度,沿y轴向上平移4个单位长度
15.如图所示,△ABC可以通过哪种方式平移得到△A1B1C1?写出一种平移方式:_________
________________________________________.
巩固提高全练
16.已知A(1,-3),B(2,-2),现将线段AB平移至线段A1B1,如果A1(a,1),B1(5,b),那么ab的值是( )
A.32 B.16 C.5 D.4
17.△ABC三个顶点的坐标分别为A(2,1),B(4,3),C(0,2),将△ABC平移到△A′B′C′的位置,其中点A′的坐标为(-1,3),则点C的坐标为( )
A.(-3,6) B.(2,-1) C.(-3,4) D.(2,5)
18.在平面直角坐标系中有一点A(-2,1),将点A先向右平移3个单位,再向下平移2个单位得到点A′,则点A′的坐标____________.
19.某景点拟在如图所示的矩形荷塘上架设小桥,若荷塘中小桥的总长为100米,则荷塘的周长为____________.
20.在平面直角坐标系中,△ABC如图所示(每个小正方形的边长均为1).
(1)请画出△ABC沿x轴向右平移4个单位长度,沿y轴向上平移2个单位长度后的△A′B'C';(其中A′、B′、C′分别是A、B、C的对应点,不写画法)
(2)直接写出A′、B′、C分三点的坐标:
A'(______,______),B'(_______,_______),C′(_______,_______);
(3)求△A′B'C′的面积.
21.如图所示,把△ABC先向右平移3个单位,再向上平移2个单位得到△DEF,则顶点C(O,-1)的对应点的坐标为( )
A.(0,0) B.(1,2) C.(1,3) D.(3,1)
22.如图所示,将△ABC沿BC方向平移至△DEF处若EC=2BE=2,则CF的长为________.
23.如图所示,在网格中,每个小正方形的边长均为1个单位长度.我们将小正方形的顶点叫做格点,△ABC的三个顶点均在格点上.
(1)将△ABC先向右平移6个单位长度,再向上平移3个单位长度,得到△A1B1C1,画出平移后的△A1B1C1.
(2)建立适当的平面直角坐标系,使得点A的坐标为(-4,3);
(3)在(2)的条件下,直接写出点A1的坐标.
24.如图所示,长方形 ABCD 中,AB=6,第 1次平移:将长方形ABCD 沿AB 的方向平移5 个单位,得到长方形A1B1C1D1,第2次平移:将长方形A1B1C1D1,沿A1B1的方向平移5个单位,得到长方形A2B2C2D2,…,第n次平移:将长方形An-1Bn-1Cn-1Dn-1沿An-1Bn-1的方向平移5个单位,得到长方形AnBnCnDn,则ABn的长为___________.(用含n的代数式表示)
25.操作与探究:
对数轴上的点 进行如下操作:先把点P表示的数乘,持把所待的效对应的点向右平移1个单位,得到点P的对应点P′.点A、B在数轴上,对线段AB 上的每个点进行上述操作后得到线段A'B′,其中点A、B的对应点分别为A′、B′.
(1)如图所示,若点A表示的数是一3,则点A′表示的数是________;若点B′表示的数是2,则点B表示的数是_________.
(2)已知线段AB上的点E经过上述操作后得到的对应点E′与点E重合,则点E表示的数是_________.
参考答案
1.D 2.B 3.C 4.C
5.解析 (1)∵△ABC平移后得到△DEF,∴∠ABC=∠E=60°,
在△ABC中,∠C=180°-∠A-∠ABC=180-80-60°=40°.
(2)OD=OB.
理由:∵AC=BC,∴∠A=∠ABC,
由平移的性质得∠A=∠EDF,
∴∠ABC=∠EDF,∴OD=OB.
6.解析 ∵将Rt△ABC沿AB方向平移得到Rt△DEF,∴△DEF≌△ABC,
∴EF=BC=10,S△DEF=S△ABC .∴S△ABC=S△DBC=S△DEF-S△DBC,S阴影=S梯形BEFG,
∵CG=3,∴BG=BC-CG=10-3=7,
∴S梯形BEFG=(BG+EF)·BE=×(7+10)×6=51,
即阴影部分的面积为51.
7.解析(1)如图所示:
(2)如图所示:
8.解析(1)△A1B1C1如图所示.
(2)如图,连接AA1,CC1,则线段AC在平移到线段A1C1的过程中,扫过的区域的面积为6×6-×4×3-×2×2-×3×4-×(4+6)×1-×3×2=36-6-2-6-5-3=14.
9.A 10.B 11.四 12. 5
13.解析 (1)由题图可知,三角形A′B′C′是由三角形 ABC 向左平移5个单位,向上平移4个单位得到的,∴点P的坐标为( a-5,b+4).
( 2) 如图所示,△A1B1C1,即为所求作的图形.
14.D 15. 先向下平移3个单位,再向左平移4个单位(答案不唯一)
16.B 17.C 18.(1, -1) 19.200米
20.解析(1)△A'B′C′如图所示:
(2)A'(2,5),B′(1,3),C′(5,0).
(3)S△A′B′C′=4×5-×1×2-×4×3-×3×5=5.5.
21.D 22. 1
23.解析 (1)如图,△A1B1C1即为所求作的图形.
(2)如图
(3)点A1的坐标为(2,6).
5n+6
解析 由题意可知,每次平移5个单位,则n次平移5n个单位,即BBn的长为5n,所以ABn=5n+AB=5n+6.
25.(1)0;3 (2)
解析(1)由已知得,点A表示的数是×(-3)+1=0.
设点B表示的数为m,则m+1=2,解得m=3,则点B表示的数为3.
(2)设点E表示的数为a,则a+1=a,解得a=,则点E表示的数为.
_21?????????è?????(www.21cnjy.com)_
第四章 图形的平移与旋转
1 图形的平移
知识能力全练
知识点一 平移的定义
1.下列现象中,属于平移的是( )
①小朋友在荡秋千; ②打气筒打气时,活塞的运动; ③风车的转动;
④瓶装饮料在传送带上移动.
A.①② B.①③ C.②③ D.②④
2.中国上海世博会吉祥物的名字叫“海宝”,意即“四海之宝”通过平移可将下图中的吉祥物“海宝”移动到( )
知识点二 平移的性质
3.在手工制作课上,张华和李丽用铁丝制作楼梯模型,如图所示,则她们用的铁丝( )
A张华的长 B.李丽的长 C.一样长 D.不能确定谁用的多
4.如图所示,将△ABC沿BC方向平移2 cm得到△DEF,连接AD,若四边形ABFD的周长为18 cm,则△ABC的周长为( )
A.10 cm B.12 cm C.14 cm D.16 cm
5.如图所示,将△ABC平移后得到△DEF.
(1)若∠A=80°,∠E=60°,求∠C的度数;
(2)若AC=BC,BC与DF相交于点O,则OD与OB相等吗?说明理由.
6.如图所示,将Rt△ABC沿AB方向平移得到Rt△DEF,已知BE=6,FE=10,CG=3,求阴影部分的面积.
知识点三 平移作图的一般步骤
7.按要求画图
(1)如图①所示,网格内每个小正方形的边长都为1个单位长度,试画出小船向右平移4个单位长度,向上平移4个单位长度后的图形;
(2)将图②中的字母A按箭头方向平移3cm,作出平移后的图形.
8.如图所示,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点A、B、C及点A1在网格的格点上,平移后点A的对应点为A1.
(1)在网格中画出△ABC平移后所得的△A1B1C1;
(2)计算线段AC在平移到线段A1C1的过程中,扫过的区域的面积.
知识点四 图形的坐标变换与平移
9.将三角形三个顶点的横坐标都减2,纵坐标不变,则所得三角形与原三角形的关系是( )
A.将原图向左平移两个单位 B.关于原点对称
C.将原图向右平移两个单位 D.关于y轴对称
10.如图所示,在平面直角坐标系xOy中,将四边形ABCD先向下平移,再向右平移,得到四边形A1B1C1D1,已知A(-3,5),B(-4,3),A1(3,3),则B1的坐标为( )
A.(1,2) B.(2,1) C.(1,4) D.(4,1)
11.在平面直角坐标系中,点P(a-4,b+8)先向右平移3个单位长度,再向下平移6个单位长度后落在第四象限内,则点(a,b)在第________象限.
12.如图所示,在平面直角坐标系中,点A的坐标为(0,4),△OAB沿x轴向右平移后得到△O′A'B′,点A的对应点A′是直线y=上的一点,则点B与其对应点B′间的距离为___________.
13.如图所示,三角形A′B'C′是由三角形ABC平移得到的.
(1)若点P(a,b)是三角形ABC内部一点,求平移后三角形A'B'C′内的对应点P′的坐标;
(2)画出将三角形ABC向左平移4个单位,向下平移1个单位得到的三角形A1B1C1.
知识点五 图形的平移变换
14.将点A(-2,3)通过以下哪种方式的平移,可以得到点A′(-5,7)( )
A.沿x轴向右平移3个单位长度,沿y轴向上平移4个单位长度
B沿x轴向左平移3个单位长度,沿y轴向下平移4个单位长度
C.沿x轴向左平移4个单位长度,沿y轴向上平移3个单位长度
D.沿x轴向左平移3个单位长度,沿y轴向上平移4个单位长度
15.如图所示,△ABC可以通过哪种方式平移得到△A1B1C1?写出一种平移方式:_________
________________________________________.
巩固提高全练
16.已知A(1,-3),B(2,-2),现将线段AB平移至线段A1B1,如果A1(a,1),B1(5,b),那么ab的值是( )
A.32 B.16 C.5 D.4
17.△ABC三个顶点的坐标分别为A(2,1),B(4,3),C(0,2),将△ABC平移到△A′B′C′的位置,其中点A′的坐标为(-1,3),则点C的坐标为( )
A.(-3,6) B.(2,-1) C.(-3,4) D.(2,5)
18.在平面直角坐标系中有一点A(-2,1),将点A先向右平移3个单位,再向下平移2个单位得到点A′,则点A′的坐标____________.
19.某景点拟在如图所示的矩形荷塘上架设小桥,若荷塘中小桥的总长为100米,则荷塘的周长为____________.
20.在平面直角坐标系中,△ABC如图所示(每个小正方形的边长均为1).
(1)请画出△ABC沿x轴向右平移4个单位长度,沿y轴向上平移2个单位长度后的△A′B'C';(其中A′、B′、C′分别是A、B、C的对应点,不写画法)
(2)直接写出A′、B′、C分三点的坐标:
A'(______,______),B'(_______,_______),C′(_______,_______);
(3)求△A′B'C′的面积.
21.如图所示,把△ABC先向右平移3个单位,再向上平移2个单位得到△DEF,则顶点C(O,-1)的对应点的坐标为( )
A.(0,0) B.(1,2) C.(1,3) D.(3,1)
22.如图所示,将△ABC沿BC方向平移至△DEF处若EC=2BE=2,则CF的长为________.
23.如图所示,在网格中,每个小正方形的边长均为1个单位长度.我们将小正方形的顶点叫做格点,△ABC的三个顶点均在格点上.
(1)将△ABC先向右平移6个单位长度,再向上平移3个单位长度,得到△A1B1C1,画出平移后的△A1B1C1.
(2)建立适当的平面直角坐标系,使得点A的坐标为(-4,3);
(3)在(2)的条件下,直接写出点A1的坐标.
24.如图所示,长方形 ABCD 中,AB=6,第 1次平移:将长方形ABCD 沿AB 的方向平移5 个单位,得到长方形A1B1C1D1,第2次平移:将长方形A1B1C1D1,沿A1B1的方向平移5个单位,得到长方形A2B2C2D2,…,第n次平移:将长方形An-1Bn-1Cn-1Dn-1沿An-1Bn-1的方向平移5个单位,得到长方形AnBnCnDn,则ABn的长为___________.(用含n的代数式表示)
25.操作与探究:
对数轴上的点 进行如下操作:先把点P表示的数乘,持把所待的效对应的点向右平移1个单位,得到点P的对应点P′.点A、B在数轴上,对线段AB 上的每个点进行上述操作后得到线段A'B′,其中点A、B的对应点分别为A′、B′.
(1)如图所示,若点A表示的数是一3,则点A′表示的数是________;若点B′表示的数是2,则点B表示的数是_________.
(2)已知线段AB上的点E经过上述操作后得到的对应点E′与点E重合,则点E表示的数是_________.
参考答案
1.D 2.B 3.C 4.C
5.解析 (1)∵△ABC平移后得到△DEF,∴∠ABC=∠E=60°,
在△ABC中,∠C=180°-∠A-∠ABC=180-80-60°=40°.
(2)OD=OB.
理由:∵AC=BC,∴∠A=∠ABC,
由平移的性质得∠A=∠EDF,
∴∠ABC=∠EDF,∴OD=OB.
6.解析 ∵将Rt△ABC沿AB方向平移得到Rt△DEF,∴△DEF≌△ABC,
∴EF=BC=10,S△DEF=S△ABC .∴S△ABC=S△DBC=S△DEF-S△DBC,S阴影=S梯形BEFG,
∵CG=3,∴BG=BC-CG=10-3=7,
∴S梯形BEFG=(BG+EF)·BE=×(7+10)×6=51,
即阴影部分的面积为51.
7.解析(1)如图所示:
(2)如图所示:
8.解析(1)△A1B1C1如图所示.
(2)如图,连接AA1,CC1,则线段AC在平移到线段A1C1的过程中,扫过的区域的面积为6×6-×4×3-×2×2-×3×4-×(4+6)×1-×3×2=36-6-2-6-5-3=14.
9.A 10.B 11.四 12. 5
13.解析 (1)由题图可知,三角形A′B′C′是由三角形 ABC 向左平移5个单位,向上平移4个单位得到的,∴点P的坐标为( a-5,b+4).
( 2) 如图所示,△A1B1C1,即为所求作的图形.
14.D 15. 先向下平移3个单位,再向左平移4个单位(答案不唯一)
16.B 17.C 18.(1, -1) 19.200米
20.解析(1)△A'B′C′如图所示:
(2)A'(2,5),B′(1,3),C′(5,0).
(3)S△A′B′C′=4×5-×1×2-×4×3-×3×5=5.5.
21.D 22. 1
23.解析 (1)如图,△A1B1C1即为所求作的图形.
(2)如图
(3)点A1的坐标为(2,6).
5n+6
解析 由题意可知,每次平移5个单位,则n次平移5n个单位,即BBn的长为5n,所以ABn=5n+AB=5n+6.
25.(1)0;3 (2)
解析(1)由已知得,点A表示的数是×(-3)+1=0.
设点B表示的数为m,则m+1=2,解得m=3,则点B表示的数为3.
(2)设点E表示的数为a,则a+1=a,解得a=,则点E表示的数为.
_21?????????è?????(www.21cnjy.com)_
