4.1 图形的平移课件(共34张PPT)
图片预览








文档简介
第四章 图形的平移与旋转
1 图形的平移
知识点一 平移的定义
在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移.平移是一种位置变化,不改变图形的形状和大小.
知识点一 平移的定义
在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移.平移是一种位置变化,不改变图形的形状和大小.
温馨提示
图形平移的条件:平移方向、平移距离.
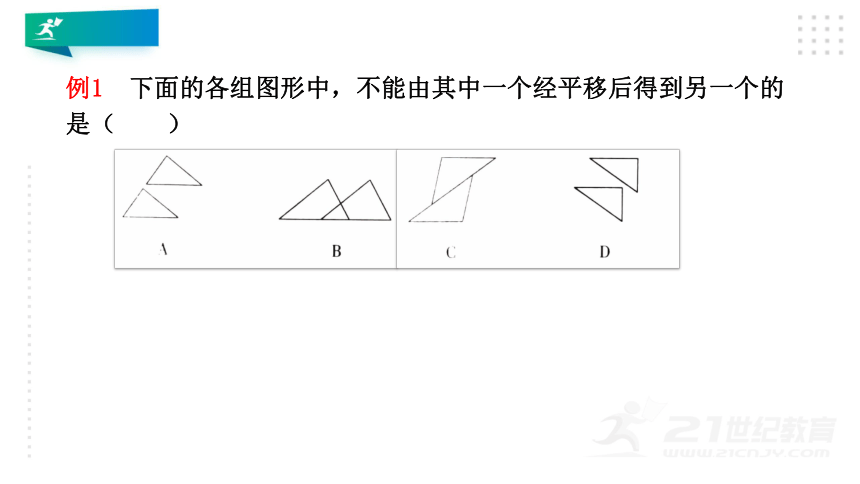
例1 下面的各组图形中,不能由其中一个经平移后得到另一个的是( )
例1 下面的各组图形中,不能由其中一个经平移后得到另一个的是( )
解析 根据平移的定义可知,C选项中的图形不能由中一个平移后得到另一个.故选C.
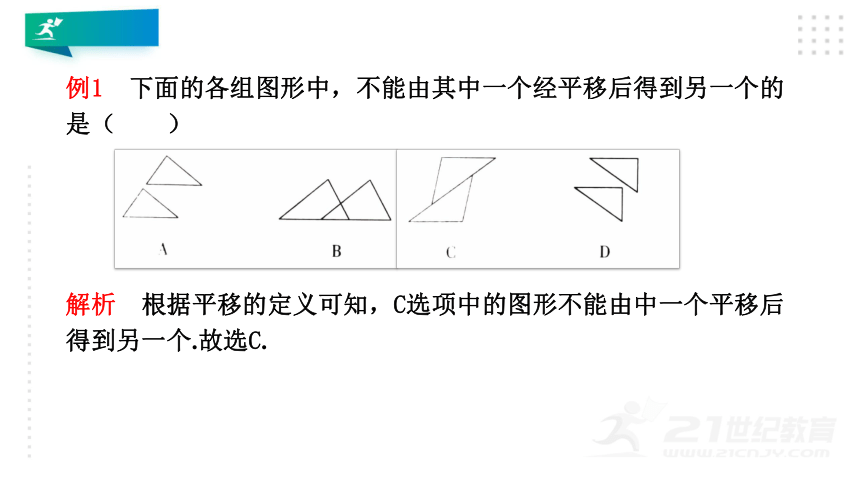
例1 下面的各组图形中,不能由其中一个经平移后得到另一个的是( C)
解析 根据平移的定义可知,C选项中的图形不能由中一个平移后得到另一个.故选C.
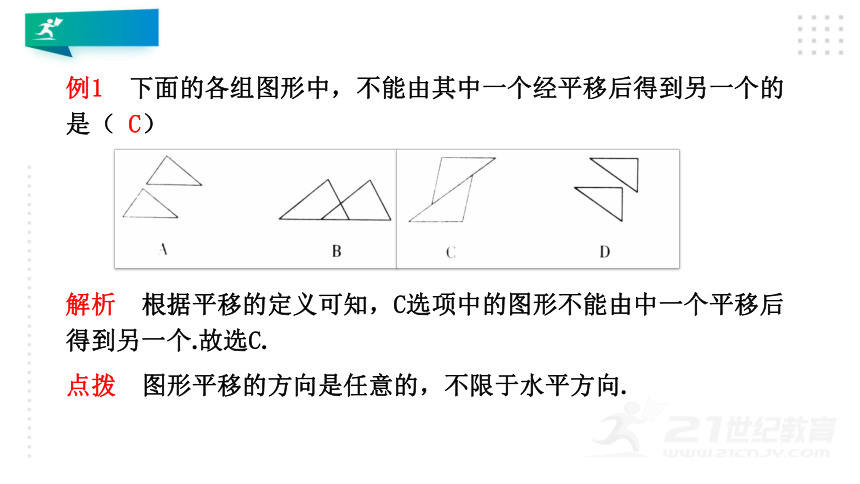
例1 下面的各组图形中,不能由其中一个经平移后得到另一个的是( C)
解析 根据平移的定义可知,C选项中的图形不能由中一个平移后得到另一个.故选C.
点拨 图形平移的方向是任意的,不限于水平方向.
知识点二 平移的性质
一个图形和它经过平移所得的图形
形状和大小完全相同,是全等形
对应点所连的线段平行(或在同一条直线上)且相等
对应线段平行(或在同一条直线上)且相等
对应角相等
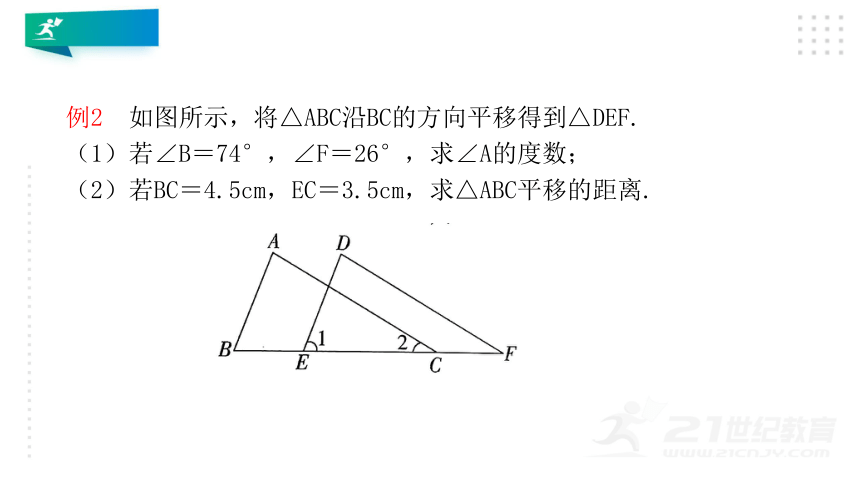
例2 如图所示,将△ABC沿BC的方向平移得到△DEF.
(1)若∠B=74°,∠F=26°,求∠A的度数;
(2)若BC=4.5cm,EC=3.5cm,求△ABC平移的距离.
分析
(1)根据平移的性质得出∠2=∠F,再利用三角形的内角和等于180°列式计算即可得解;
(2)先求出BE的长,再根据平移的性质可得平移的距离.
解析 (1)由图形平移的性质,可知△ABC和△DEF的形状与大小相同,
即△ABC≌△DEF,∴∠2=∠F=26°,:∠B=74°,
∴∠A=180°-(∠2+∠B)=180-(26+74°)=80°.
(2)∵BC=4.5cm,EC=3.5cm,
∴BE=BC-EC=4.5-3.5=1 cm.
∴△ABC平移的距离为1cm.
点拨
根据平移的性质“平移不改变图形的形状和大小,对应点所连的线段平行(或在同一条直线上)且相等”来解决问题.
知识点三 平移作图的一般步骤
例3 如图所示,将正三角形ABC平移,使点A到达点D的位置.
解析 如图,连接AD,过B作BE∥AD,且使BE=AD,过C作CF∥AD,且使CF=AD,分别得到点E、F,顺次连接DE、EF、FD得到△DEF,△DEF即为所求作的图形.
点拨
本题考查的是平移变换作图平移作图时,找到原图形中的关键点并画出平移后的对应点是关键.
知识点四 图形的坐标变换与平移
设点P(x,y)在原图形上,经过平移后,这点与其对应点的坐标之间有如下关系:
平移方向
平移距离
对应点的坐标
沿x轴方向
向右平移
m个单位长度(m>0)
P1(x+m,y)
向左平移
P2(x-m,y)
沿y轴方向
向上平移
n个单位长度(n>0)
P3(x,y+n)
向下平移
P4(x,y-n)
例4 △ABC与△A′B′C′在平面直角坐标系中的位置如图所示.
(1)分别写出下列各点的坐标:A′__________,B′___________,C′__________;
(2)说明△A′B′C′是由△ABC经过怎样的平移得到的:_____________
___________________________________;
(3)若点P(a,b)是△ABC内部一点,则平移后△A′B′C′内的对应点P′的坐标为_____________;
(4)求△ABC的面积.
分析
(1)直接写出各点坐标即可.
(2)利用对应点的位置得出平移规律.
(3)利用(2)中的平移规律得出答案.
(4)利用△ABC所在矩形的面积减去周围三角形的面积得出答案.
知识点五 图形的平移变换
名称
定义
方法
图形的平移变换
一个图形依次沿x轴方向、y轴方向平移后所得的图形,可以看成是由原来的图形经过一次平移得到的
(1)一次平移的方向是由原图形上的点到平移后图形上的对应点的方向;
(2)若沿x轴方向平移了a(a>0)个单位长度,沿y轴方向平移了b(b>0)个单位长度,则原图形一次平移的距离为 .
例5 在平面直角坐标系中,已知点P(1,1)先向右平移一个单位长度,再向上平移一个单位长度,到达点Q的位置.(1)写出点Q的坐标;(2)两次平移的结果也可以看成是点P沿哪个方向平移了几个单位长度直接到达点Q的位置的?
经典例题
题型一 平移性质的应用
例1 如图所示,三角形EFG是由三角形ABC沿箭头方向平移得到的.
(1)若∠BAC=30°,求∠FEG的度数;
(2)若EG=2cm,求AC的长;
(3)若AE=2.5cm,求BF,CG的长.
题型一 平移性质的应用
解析 ∵三角形EFG是由三角形ABC沿箭头方向平移得到的,
∴点E与点A对应,点F与点B对应,点G与点C对应.
∴∠FEG=∠BAC,EG=AC,AE=BF=CG.
(1)∵∠BAC=30°,∴∠FEG=30°.
(2)∵EG=2cm,∴AC=EG=2cm.
(3)∵AE=2.5 cm,∴BF=CG=2.5 cm.
题型一 平移性质的应用
解析 ∵三角形EFG是由三角形ABC沿箭头方向平移得到的,
∴点E与点A对应,点F与点B对应,点G与点C对应.
∴∠FEG=∠BAC,EG=AC,AE=BF=CG.
(1)∵∠BAC=30°,∴∠FEG=30°.
(2)∵EG=2cm,∴AC=EG=2cm.
(3)∵AE=2.5 cm,∴BF=CG=2.5 cm.
点拨 根据平移的性质:“平移不改变图形的形状和大小,且对应点所连的线段平行(或在一条直线上)且相等”来解决问题.
题型二 网格中的平移
例2 如图所示,在平面直角坐标系中,已知点A(-3,3),B(-5,1),C(-2,0),P(a,b)是△ABC的边AC上任意一点,△ABC经过平移后得到△A1B1C1,点P的对应点为P1(a+6,b-2).(1)写出点A1,B1,C1的坐标;
(2)在图中画出△A1B1C1;
(3)连接OA,OA1,AA1,
求△AOA1的面积.
分析
(1)先根据点P、P1的坐标确定平移规律,再求出A1,B1,C1的坐标即可;
(2)顺次连接A1,B1,C1即可;
(3)利用△AOA1所在的矩形的面积减去四周三个小直角三角形的面积,列式计算即可.
点拨
一对对应点平移的方向和距离代表了整个图形的平移方向和距离,以“局部带整体”可作出符合条件的平移图形.
1 图形的平移
知识点一 平移的定义
在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移.平移是一种位置变化,不改变图形的形状和大小.
知识点一 平移的定义
在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移.平移是一种位置变化,不改变图形的形状和大小.
温馨提示
图形平移的条件:平移方向、平移距离.
例1 下面的各组图形中,不能由其中一个经平移后得到另一个的是( )
例1 下面的各组图形中,不能由其中一个经平移后得到另一个的是( )
解析 根据平移的定义可知,C选项中的图形不能由中一个平移后得到另一个.故选C.
例1 下面的各组图形中,不能由其中一个经平移后得到另一个的是( C)
解析 根据平移的定义可知,C选项中的图形不能由中一个平移后得到另一个.故选C.
例1 下面的各组图形中,不能由其中一个经平移后得到另一个的是( C)
解析 根据平移的定义可知,C选项中的图形不能由中一个平移后得到另一个.故选C.
点拨 图形平移的方向是任意的,不限于水平方向.
知识点二 平移的性质
一个图形和它经过平移所得的图形
形状和大小完全相同,是全等形
对应点所连的线段平行(或在同一条直线上)且相等
对应线段平行(或在同一条直线上)且相等
对应角相等
例2 如图所示,将△ABC沿BC的方向平移得到△DEF.
(1)若∠B=74°,∠F=26°,求∠A的度数;
(2)若BC=4.5cm,EC=3.5cm,求△ABC平移的距离.
分析
(1)根据平移的性质得出∠2=∠F,再利用三角形的内角和等于180°列式计算即可得解;
(2)先求出BE的长,再根据平移的性质可得平移的距离.
解析 (1)由图形平移的性质,可知△ABC和△DEF的形状与大小相同,
即△ABC≌△DEF,∴∠2=∠F=26°,:∠B=74°,
∴∠A=180°-(∠2+∠B)=180-(26+74°)=80°.
(2)∵BC=4.5cm,EC=3.5cm,
∴BE=BC-EC=4.5-3.5=1 cm.
∴△ABC平移的距离为1cm.
点拨
根据平移的性质“平移不改变图形的形状和大小,对应点所连的线段平行(或在同一条直线上)且相等”来解决问题.
知识点三 平移作图的一般步骤
例3 如图所示,将正三角形ABC平移,使点A到达点D的位置.
解析 如图,连接AD,过B作BE∥AD,且使BE=AD,过C作CF∥AD,且使CF=AD,分别得到点E、F,顺次连接DE、EF、FD得到△DEF,△DEF即为所求作的图形.
点拨
本题考查的是平移变换作图平移作图时,找到原图形中的关键点并画出平移后的对应点是关键.
知识点四 图形的坐标变换与平移
设点P(x,y)在原图形上,经过平移后,这点与其对应点的坐标之间有如下关系:
平移方向
平移距离
对应点的坐标
沿x轴方向
向右平移
m个单位长度(m>0)
P1(x+m,y)
向左平移
P2(x-m,y)
沿y轴方向
向上平移
n个单位长度(n>0)
P3(x,y+n)
向下平移
P4(x,y-n)
例4 △ABC与△A′B′C′在平面直角坐标系中的位置如图所示.
(1)分别写出下列各点的坐标:A′__________,B′___________,C′__________;
(2)说明△A′B′C′是由△ABC经过怎样的平移得到的:_____________
___________________________________;
(3)若点P(a,b)是△ABC内部一点,则平移后△A′B′C′内的对应点P′的坐标为_____________;
(4)求△ABC的面积.
分析
(1)直接写出各点坐标即可.
(2)利用对应点的位置得出平移规律.
(3)利用(2)中的平移规律得出答案.
(4)利用△ABC所在矩形的面积减去周围三角形的面积得出答案.
知识点五 图形的平移变换
名称
定义
方法
图形的平移变换
一个图形依次沿x轴方向、y轴方向平移后所得的图形,可以看成是由原来的图形经过一次平移得到的
(1)一次平移的方向是由原图形上的点到平移后图形上的对应点的方向;
(2)若沿x轴方向平移了a(a>0)个单位长度,沿y轴方向平移了b(b>0)个单位长度,则原图形一次平移的距离为 .
例5 在平面直角坐标系中,已知点P(1,1)先向右平移一个单位长度,再向上平移一个单位长度,到达点Q的位置.(1)写出点Q的坐标;(2)两次平移的结果也可以看成是点P沿哪个方向平移了几个单位长度直接到达点Q的位置的?
经典例题
题型一 平移性质的应用
例1 如图所示,三角形EFG是由三角形ABC沿箭头方向平移得到的.
(1)若∠BAC=30°,求∠FEG的度数;
(2)若EG=2cm,求AC的长;
(3)若AE=2.5cm,求BF,CG的长.
题型一 平移性质的应用
解析 ∵三角形EFG是由三角形ABC沿箭头方向平移得到的,
∴点E与点A对应,点F与点B对应,点G与点C对应.
∴∠FEG=∠BAC,EG=AC,AE=BF=CG.
(1)∵∠BAC=30°,∴∠FEG=30°.
(2)∵EG=2cm,∴AC=EG=2cm.
(3)∵AE=2.5 cm,∴BF=CG=2.5 cm.
题型一 平移性质的应用
解析 ∵三角形EFG是由三角形ABC沿箭头方向平移得到的,
∴点E与点A对应,点F与点B对应,点G与点C对应.
∴∠FEG=∠BAC,EG=AC,AE=BF=CG.
(1)∵∠BAC=30°,∴∠FEG=30°.
(2)∵EG=2cm,∴AC=EG=2cm.
(3)∵AE=2.5 cm,∴BF=CG=2.5 cm.
点拨 根据平移的性质:“平移不改变图形的形状和大小,且对应点所连的线段平行(或在一条直线上)且相等”来解决问题.
题型二 网格中的平移
例2 如图所示,在平面直角坐标系中,已知点A(-3,3),B(-5,1),C(-2,0),P(a,b)是△ABC的边AC上任意一点,△ABC经过平移后得到△A1B1C1,点P的对应点为P1(a+6,b-2).(1)写出点A1,B1,C1的坐标;
(2)在图中画出△A1B1C1;
(3)连接OA,OA1,AA1,
求△AOA1的面积.
分析
(1)先根据点P、P1的坐标确定平移规律,再求出A1,B1,C1的坐标即可;
(2)顺次连接A1,B1,C1即可;
(3)利用△AOA1所在的矩形的面积减去四周三个小直角三角形的面积,列式计算即可.
点拨
一对对应点平移的方向和距离代表了整个图形的平移方向和距离,以“局部带整体”可作出符合条件的平移图形.
