人教A版(2019)选择性必修第一册《12_空间向量基本定理》2021年同步练习卷(5)(Word含解析)
文档属性
| 名称 | 人教A版(2019)选择性必修第一册《12_空间向量基本定理》2021年同步练习卷(5)(Word含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 260.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-14 09:03:27 | ||
图片预览



文档简介
人教A版(2019)选择性必修第一册《1.2
空间向量基本定理》2021年同步练习卷(5)
一、选择题
?
1.
若向量是空间的一个基底,则一定可以与向量构成空间的另一个基底的向量是(
)
A.
B.
C.
D.
?
2.
如图,在平行六面体中,为与的交点,若,,.则下列向量中与相等的向量是
A.
B.
C.
D.
?
3.
若向量的起点和终点,,互不重合,且无三点共线,则能使向量成为空间一个基底的关系式是(
)
A.
B.
C.
D.
?
4.
如图所示,在四面体中,,,,点在上,且=,为的中点,则=(
)
A.-+
B.-++
C.
D.
?
5.
在平行六面体中,向量,,两两的夹角均为,且,,,则等于(?
?
?
?
)
A.
B.
C.
D.
二、填空题
?
在四面体中,,,,为的中点,为的中点,则________(用,,表示)
?
已知{,,}是空间的一个单位正交基底,{+,-,}是空间的另一个基底,若向量在基底{,,}下表示为=,则在基底,{+,-,}下可表示为________.
?
在四棱锥中,为平行四边形,与交于,为上一点,=,=,=,=,试用基底{,,}表示向量=________.
三、解答题
?
如图所示,正方体,且=,=,=.
(1)用,,表示向量,;
(2)设,分别是侧面和的中心,用,,表示.
?
如图,在平行六面体中,=-,=,设=,=,=,试用,,表示.
四、选择题
?
已知,,是不共面的三个向量,则下列向量组中,不能构成一个基底的一组向量是(
)
A.,-,
B.,-,
C.,,-
D.,+,-
?
给出下列命题,其中是真命题的是(
)
A.若{,,}可以作为空间的一个基底,与共线,,则{,,}也可以作为空间的一个基底
B.已知向量,则,与任何向量都不能构成空间的一个基底
C.已知,,,是空间中的四点,若,,不能构成空间的一个基底,则,,,四点共面
D.已知{,,}是空间的一个基底,若=+,则{,,}也是空间的一个基底
五、填空题
?
已知空间的一个基底{,,},=-+,=+,若与共线,则=________,=________.
?
已知是空间单位向量,,若空间向量满足,且对于任意,,,则________,________,________.
?
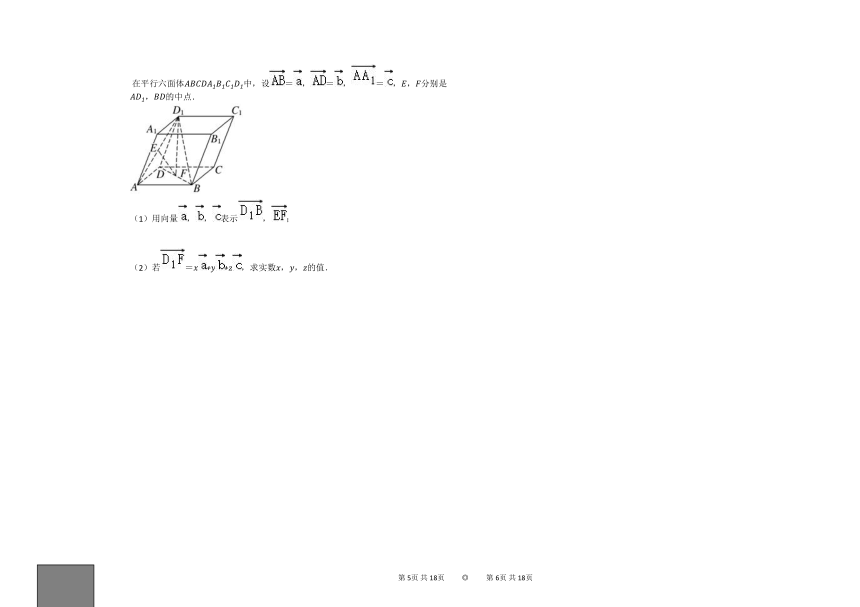
在平行六面体中,设=,=,=,,分别是,的中点.
(1)用向量,,表示,;
(2)若=,求实数,,的值.
参考答案与试题解析
人教A版(2019)选择性必修第一册《1.2
空间向量基本定理》2021年同步练习卷(5)
一、选择题
1.
【答案】
C
【考点】
空间向量的基本定理及其意义
【解析】
空间向量的一组基底,要满足不为零向量,且三个向量不共面,逐个判断即可.
【解答】
解:由已知及向量共面定理,结合,
可知向量,,共面,同理可得,
故向量,,共面,故向量,都不可能与,构成基底,
又可得,
故向量也不可能与,构成基底,只有符合题意,
故选
2.
【答案】
A
【考点】
向量加减混合运算及其几何意义
相等向量与相反向量
【解析】
由题意可得,化简得到结果.
【解答】
解:由题意可得
,
故选.
3.
【答案】
C
【考点】
平面向量的基本定理及其意义
【解析】
.由,,利用平面向量基本定理可知:点在平面内;
.由,利用平面向量基本定理可知:向量,,共面;
.由,且向量,,的起点与终点、、互不重合且无三点共线,由空间平行六面体法则即可判断出;
.由可知:向量,,共面.
【解答】
解:.∵
,,
∴
点在平面内,
因此向量,,不能构成一个空间基底;
.∵
,
∴
向量,,共面,不能构成一个空间基底;
.由,且向量,,的起点与终点、、互不重合且无三点共线,
由空间平行六面体法则可知:
是以点为顶点的对角线,
∴
向量,,能构成一个空间基底;
.由可知:向量,,共面,
因此不能构成空间的一个基底.
综上可得:只有正确.
故选:.
4.
【答案】
B
【考点】
平面向量的基本定理
【解析】
根据向量加法和减法的三角形法则得出.
【解答】
连接,
∵
是的中点,∴
=,
∵
=,∴
=,
∴
==-=-++,
5.
【答案】
A
【考点】
平面向量的夹角
向量在几何中的应用
【解析】
由题设知,故,由此能求出.
【解答】
解:如图,
∵
在平行六面体中,?
向量、、两两的夹角均为,
且,,,
∴
,
∴
,
∴
.
故选A.
二、填空题
【答案】
【考点】
空间向量的加减法
中点坐标公式
【解析】
利用为的中点,为的中点,,,化简可得结果.
【解答】
解:在四面体中,,,,为的中点,为的中点,
∴
,
故答案为:.
【答案】
=(+)-(-))
【考点】
空间向量的基本定理及其意义
空间向量的正交分解及其坐标表示
【解析】
设=(+)(-)),利用向量相等列方程组求出、、的值即可.
【解答】
由题意知,=,
设=(+-)),
所以=,
由向量相等得,
解得;
所以在基底{+,-,
=(+)-(-).
【答案】
【考点】
空间向量的基本定理及其意义
空间向量的正交分解及其坐标表示
【解析】
由题意画出图形,然后利用向量加减法的三角形法则求得.
【解答】
如图,
=
=.
三、解答题
【答案】
正方体,且=,=,=.
所以,
.
根据三角形法则:连接和,
【考点】
空间向量的基本定理及其意义
空间向量的正交分解及其坐标表示
【解析】
(1)直接利用三角形法则和向量的线性运算的应用求出结果.
(2)直接利用三角形法则和向量的线性运算的应用求出结果.
【解答】
正方体,且=,=,=.
所以,
.
根据三角形法则:连接和,
【答案】
连接,
∴
=+,
∵
=-(+),=+=+(-)=+,
∴
=-(++=-++.
【考点】
空间向量的基本定理及其意义
空间向量的正交分解及其坐标表示
【解析】
根据向量的加减的几何意义即可求出.
【解答】
连接,
∴
=+,
∵
=-(+),=+=+(-)=+,
∴
=-(++=-++.
四、选择题
【答案】
A,B,D
【考点】
空间向量的基本定理及其意义
空间向量的正交分解及其坐标表示
平面向量的基本定理
【解析】
分别判断向量是否共面即可.
【解答】
,因为=(-()、-、,故它们不能构成一个基底;
,因为=(-()、-、,故它们不能构成一个基底;
,因为找不到实数、,使(-,故、、-三个向量不共面;
对于,因为=(+(-),得、+、-三个向量共面,
【答案】
A,B,C,D
【考点】
命题的真假判断与应用
【解析】
直接利用向量的基底的定义,向量的共线,共面向量的充要条件判定、、、的结果.
【解答】
对于选项:若{,,}可以作为空间的一个基底,与,,则{,,,真命题.
对于选项:已知向量,则,与任何向量都不能构成空间的一个基底.
对于选项:已知,,,是空间中的四点,若,,,则,,,真命题.
对于选项:已知{,,}是空间的一个基底,若=+,,}也是空间的一个基底.
五、填空题
【答案】
,
【考点】
共线向量与共面向量
【解析】
由与共线,得存在实数,使,列出方程组能求出结果.
【解答】
因为空间的一个基底{,,},
=-+,=+,与共线,
所以存在实数,使,
即-+=,
∴
,解得.
【答案】
,,
【考点】
空间向量的数量积运算
平面向量数量积的运算
【解析】
由题意和数量积的运算可得,不妨设,,由已知可解,可得,由题意可得当,时,取最小值,由模长公式可得.
【解答】
解:∵
,
∴
,不妨设,,,
则由题意可知,,解得,,∴
,
∵
,
∴
,
由题意当,时,取最小值,
此时,故
故答案为:;;
【答案】
如图,=+=-+-=--,
=+=+
=-(+)+(+(-).
=(+)
=(-+)
=(-+--)
=--,
∴
=,=-.
【考点】
数量积表示两个向量的夹角
平面向量的基本定理
【解析】
(1)如图,=+=-+-,=+=+=-(+)+(+),进而得到答案;
(2)=(+)=(-+),结合=,可得实数,,的值.
【解答】
如图,=+=-+-=--,
=+=+
=-(+)+(+(-).
=(+)
=(-+)
=(-+--)
=--,
∴
=,=-.
第7页
共20页
◎
第8页
共20页
第9页
共20页
◎
第10页
共20页
空间向量基本定理》2021年同步练习卷(5)
一、选择题
?
1.
若向量是空间的一个基底,则一定可以与向量构成空间的另一个基底的向量是(
)
A.
B.
C.
D.
?
2.
如图,在平行六面体中,为与的交点,若,,.则下列向量中与相等的向量是
A.
B.
C.
D.
?
3.
若向量的起点和终点,,互不重合,且无三点共线,则能使向量成为空间一个基底的关系式是(
)
A.
B.
C.
D.
?
4.
如图所示,在四面体中,,,,点在上,且=,为的中点,则=(
)
A.-+
B.-++
C.
D.
?
5.
在平行六面体中,向量,,两两的夹角均为,且,,,则等于(?
?
?
?
)
A.
B.
C.
D.
二、填空题
?
在四面体中,,,,为的中点,为的中点,则________(用,,表示)
?
已知{,,}是空间的一个单位正交基底,{+,-,}是空间的另一个基底,若向量在基底{,,}下表示为=,则在基底,{+,-,}下可表示为________.
?
在四棱锥中,为平行四边形,与交于,为上一点,=,=,=,=,试用基底{,,}表示向量=________.
三、解答题
?
如图所示,正方体,且=,=,=.
(1)用,,表示向量,;
(2)设,分别是侧面和的中心,用,,表示.
?
如图,在平行六面体中,=-,=,设=,=,=,试用,,表示.
四、选择题
?
已知,,是不共面的三个向量,则下列向量组中,不能构成一个基底的一组向量是(
)
A.,-,
B.,-,
C.,,-
D.,+,-
?
给出下列命题,其中是真命题的是(
)
A.若{,,}可以作为空间的一个基底,与共线,,则{,,}也可以作为空间的一个基底
B.已知向量,则,与任何向量都不能构成空间的一个基底
C.已知,,,是空间中的四点,若,,不能构成空间的一个基底,则,,,四点共面
D.已知{,,}是空间的一个基底,若=+,则{,,}也是空间的一个基底
五、填空题
?
已知空间的一个基底{,,},=-+,=+,若与共线,则=________,=________.
?
已知是空间单位向量,,若空间向量满足,且对于任意,,,则________,________,________.
?
在平行六面体中,设=,=,=,,分别是,的中点.
(1)用向量,,表示,;
(2)若=,求实数,,的值.
参考答案与试题解析
人教A版(2019)选择性必修第一册《1.2
空间向量基本定理》2021年同步练习卷(5)
一、选择题
1.
【答案】
C
【考点】
空间向量的基本定理及其意义
【解析】
空间向量的一组基底,要满足不为零向量,且三个向量不共面,逐个判断即可.
【解答】
解:由已知及向量共面定理,结合,
可知向量,,共面,同理可得,
故向量,,共面,故向量,都不可能与,构成基底,
又可得,
故向量也不可能与,构成基底,只有符合题意,
故选
2.
【答案】
A
【考点】
向量加减混合运算及其几何意义
相等向量与相反向量
【解析】
由题意可得,化简得到结果.
【解答】
解:由题意可得
,
故选.
3.
【答案】
C
【考点】
平面向量的基本定理及其意义
【解析】
.由,,利用平面向量基本定理可知:点在平面内;
.由,利用平面向量基本定理可知:向量,,共面;
.由,且向量,,的起点与终点、、互不重合且无三点共线,由空间平行六面体法则即可判断出;
.由可知:向量,,共面.
【解答】
解:.∵
,,
∴
点在平面内,
因此向量,,不能构成一个空间基底;
.∵
,
∴
向量,,共面,不能构成一个空间基底;
.由,且向量,,的起点与终点、、互不重合且无三点共线,
由空间平行六面体法则可知:
是以点为顶点的对角线,
∴
向量,,能构成一个空间基底;
.由可知:向量,,共面,
因此不能构成空间的一个基底.
综上可得:只有正确.
故选:.
4.
【答案】
B
【考点】
平面向量的基本定理
【解析】
根据向量加法和减法的三角形法则得出.
【解答】
连接,
∵
是的中点,∴
=,
∵
=,∴
=,
∴
==-=-++,
5.
【答案】
A
【考点】
平面向量的夹角
向量在几何中的应用
【解析】
由题设知,故,由此能求出.
【解答】
解:如图,
∵
在平行六面体中,?
向量、、两两的夹角均为,
且,,,
∴
,
∴
,
∴
.
故选A.
二、填空题
【答案】
【考点】
空间向量的加减法
中点坐标公式
【解析】
利用为的中点,为的中点,,,化简可得结果.
【解答】
解:在四面体中,,,,为的中点,为的中点,
∴
,
故答案为:.
【答案】
=(+)-(-))
【考点】
空间向量的基本定理及其意义
空间向量的正交分解及其坐标表示
【解析】
设=(+)(-)),利用向量相等列方程组求出、、的值即可.
【解答】
由题意知,=,
设=(+-)),
所以=,
由向量相等得,
解得;
所以在基底{+,-,
=(+)-(-).
【答案】
【考点】
空间向量的基本定理及其意义
空间向量的正交分解及其坐标表示
【解析】
由题意画出图形,然后利用向量加减法的三角形法则求得.
【解答】
如图,
=
=.
三、解答题
【答案】
正方体,且=,=,=.
所以,
.
根据三角形法则:连接和,
【考点】
空间向量的基本定理及其意义
空间向量的正交分解及其坐标表示
【解析】
(1)直接利用三角形法则和向量的线性运算的应用求出结果.
(2)直接利用三角形法则和向量的线性运算的应用求出结果.
【解答】
正方体,且=,=,=.
所以,
.
根据三角形法则:连接和,
【答案】
连接,
∴
=+,
∵
=-(+),=+=+(-)=+,
∴
=-(++=-++.
【考点】
空间向量的基本定理及其意义
空间向量的正交分解及其坐标表示
【解析】
根据向量的加减的几何意义即可求出.
【解答】
连接,
∴
=+,
∵
=-(+),=+=+(-)=+,
∴
=-(++=-++.
四、选择题
【答案】
A,B,D
【考点】
空间向量的基本定理及其意义
空间向量的正交分解及其坐标表示
平面向量的基本定理
【解析】
分别判断向量是否共面即可.
【解答】
,因为=(-()、-、,故它们不能构成一个基底;
,因为=(-()、-、,故它们不能构成一个基底;
,因为找不到实数、,使(-,故、、-三个向量不共面;
对于,因为=(+(-),得、+、-三个向量共面,
【答案】
A,B,C,D
【考点】
命题的真假判断与应用
【解析】
直接利用向量的基底的定义,向量的共线,共面向量的充要条件判定、、、的结果.
【解答】
对于选项:若{,,}可以作为空间的一个基底,与,,则{,,,真命题.
对于选项:已知向量,则,与任何向量都不能构成空间的一个基底.
对于选项:已知,,,是空间中的四点,若,,,则,,,真命题.
对于选项:已知{,,}是空间的一个基底,若=+,,}也是空间的一个基底.
五、填空题
【答案】
,
【考点】
共线向量与共面向量
【解析】
由与共线,得存在实数,使,列出方程组能求出结果.
【解答】
因为空间的一个基底{,,},
=-+,=+,与共线,
所以存在实数,使,
即-+=,
∴
,解得.
【答案】
,,
【考点】
空间向量的数量积运算
平面向量数量积的运算
【解析】
由题意和数量积的运算可得,不妨设,,由已知可解,可得,由题意可得当,时,取最小值,由模长公式可得.
【解答】
解:∵
,
∴
,不妨设,,,
则由题意可知,,解得,,∴
,
∵
,
∴
,
由题意当,时,取最小值,
此时,故
故答案为:;;
【答案】
如图,=+=-+-=--,
=+=+
=-(+)+(+(-).
=(+)
=(-+)
=(-+--)
=--,
∴
=,=-.
【考点】
数量积表示两个向量的夹角
平面向量的基本定理
【解析】
(1)如图,=+=-+-,=+=+=-(+)+(+),进而得到答案;
(2)=(+)=(-+),结合=,可得实数,,的值.
【解答】
如图,=+=-+-=--,
=+=+
=-(+)+(+(-).
=(+)
=(-+)
=(-+--)
=--,
∴
=,=-.
第7页
共20页
◎
第8页
共20页
第9页
共20页
◎
第10页
共20页
