2021-2022学年苏科版九年级数学上册第2章对称图形——圆单元测试卷(Word版,附答案解析)
文档属性
| 名称 | 2021-2022学年苏科版九年级数学上册第2章对称图形——圆单元测试卷(Word版,附答案解析) |  | |
| 格式 | zip | ||
| 文件大小 | 325.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-16 00:06:31 | ||
图片预览



文档简介
2021-2022学年苏科新版九年级上册数学《第2章
对称图形——圆》单元测试卷
一.选择题
1.已知⊙O的半径为5cm,P为⊙O外一点,则OP的长可能是( )
A.5
cm
B.4
cm
C.3
cm
D.6
cm
2.如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=20,CD=16,那么线段OE的长为( )
A.10
B.8
C.6
D.4
3.把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=4cm,则球的半径长是( )
A.2cm
B.2.5cm
C.3cm
D.4cm
4.下列说法正确的是( )
A.一个点可以确定一条直线
B.两个点可以确定两条直线
C.三个点可以确定一个圆
D.不在同一直线上的三点确定一个圆
5.下列命题错误的是( )
A.经过三个点一定可以作圆
B.三角形的外心到三角形各顶点的距离相等
C.同圆或等圆中,相等的圆心角所对的弧相等
D.经过切点且垂直于切线的直线必经过圆心
6.已知AB是⊙O的弦,⊙O的半径为r,下列关系式一定成立的是( )
A.AB>r
B.AB<r
C.AB<2r
D.AB≤2r
7.半径为2的圆中,弦AB、AC的长分别2和2,则∠BAC的度数是( )
A.15°
B.15°或45°
C.15°或75°
D.15°或105°
8.如图,在半径为3的⊙O中,AB是直径,AC是弦,D是的中点,AC与BD交于点E.若E是BD的中点,则AC的长是( )
A.
B.3
C.3
D.4
9.如图,一个小圆沿着一个五边形的边滚动,如果五边形的各边长都和小圆的周长相等,那么当小圆滚动到原来位置时,小圆自身滚动的圈数是( )
A.4
B.5
C.6
D.10
10.如图在⊙O中,若点C是的中点,∠AOC=45°,则∠AOB=( )
A.45°
B.80°
C.85°
D.90°
二.填空题
11.如图,△ABC中,∠ACB=90°,∠A=40°,以C为圆心、CB为半径的圆交AB于点D,则∠ACD=
度.
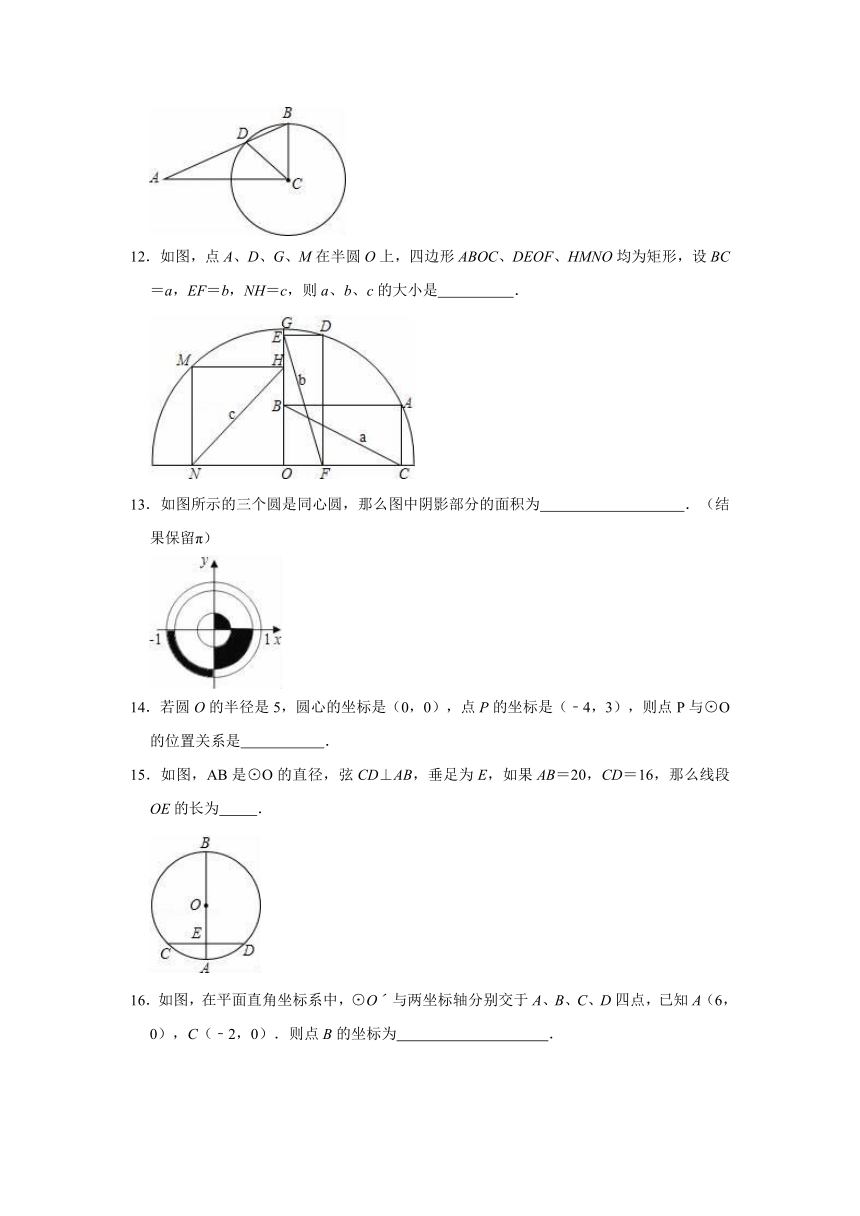
12.如图,点A、D、G、M在半圆O上,四边形ABOC、DEOF、HMNO均为矩形,设BC=a,EF=b,NH=c,则a、b、c的大小是
.
13.如图所示的三个圆是同心圆,那么图中阴影部分的面积为
.(结果保留π)
14.若圆O的半径是5,圆心的坐标是(0,0),点P的坐标是(﹣4,3),则点P与⊙O的位置关系是
.
15.如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=20,CD=16,那么线段OE的长为
.
16.如图,在平面直角坐标系中,⊙Oˊ与两坐标轴分别交于A、B、C、D四点,已知A(6,0),C(﹣2,0).则点B的坐标为
.
17.根据“不在同一直线上的三点确定一个圆”,可以判断平面直角坐标系内的三个点A(3,0)、B(0,﹣4)、C(2,﹣3)
确定一个圆(填“能”或“不能”).
18.某公路上有一隧道,顶部是圆弧形拱顶,圆心为O,隧道的水平宽AB为24m,AB离地面的高度AE=10
m,拱顶最高处C离地面的高度CD为18m,在拱顶的M,N处安装照明灯,且M,N离地面的高度相等都等于17m,则MN=
m.
19.正方形的四个顶点和它的中心共5个点能确定
个不同的圆.
20.如图,在四边形ABCD中,∠BAD=∠CDA=90°,AB=1,CD=2,过A,B,D三点的⊙O分别交BC,CD于点E,M,下列结论:①DM=CM;②;③⊙O的直径为2;④AE=AD.其中正确的结论有
(填序号).
三.解答题
21.已知:如图,AB是⊙O的直径,点C、D在⊙O上,CE⊥AB于E,DF⊥AB于F,且AE=BF,AC与BD相等吗?为什么?
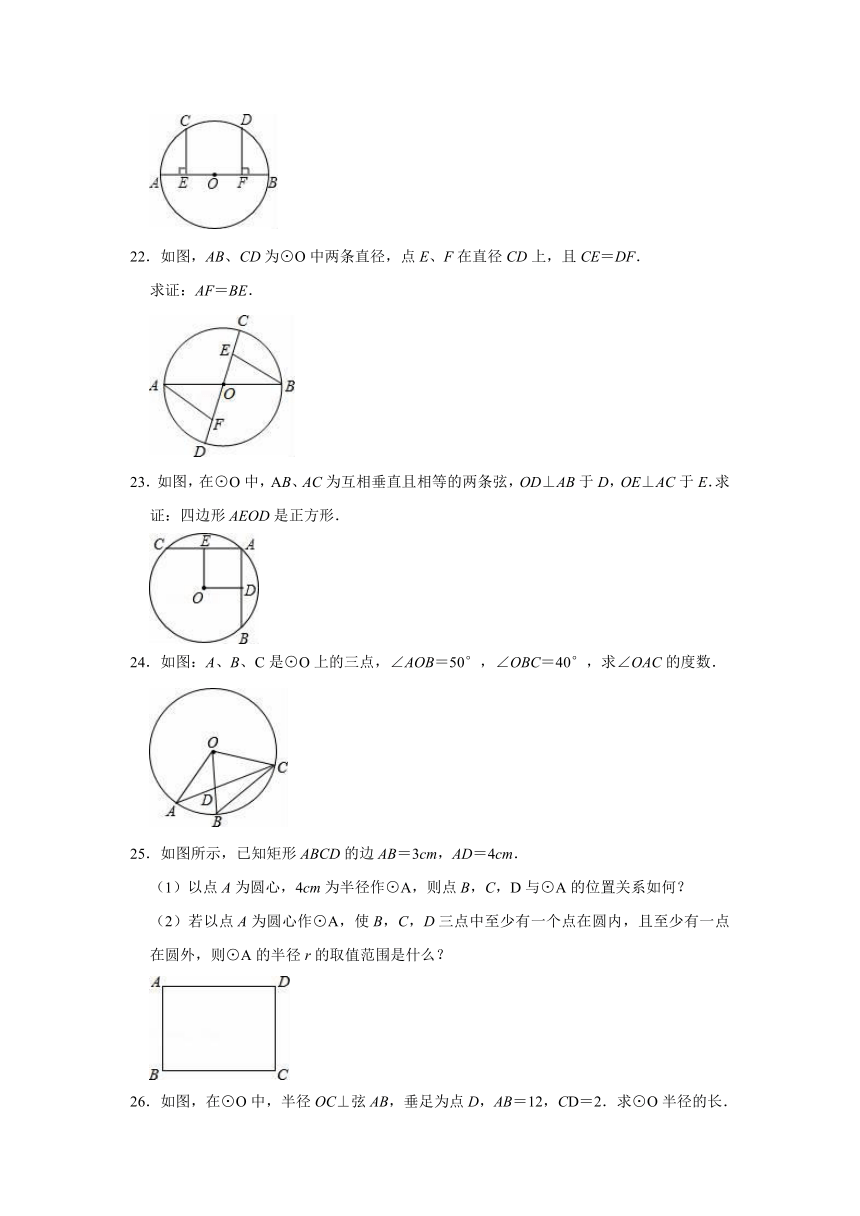
22.如图,AB、CD为⊙O中两条直径,点E、F在直径CD上,且CE=DF.
求证:AF=BE.
23.如图,在⊙O中,AB、AC为互相垂直且相等的两条弦,OD⊥AB于D,OE⊥AC于E.求证:四边形AEOD是正方形.
24.如图:A、B、C是⊙O上的三点,∠AOB=50°,∠OBC=40°,求∠OAC的度数.
25.如图所示,已知矩形ABCD的边AB=3cm,AD=4cm.
(1)以点A为圆心,4cm为半径作⊙A,则点B,C,D与⊙A的位置关系如何?
(2)若以点A为圆心作⊙A,使B,C,D三点中至少有一个点在圆内,且至少有一点在圆外,则⊙A的半径r的取值范围是什么?
26.如图,在⊙O中,半径OC⊥弦AB,垂足为点D,AB=12,CD=2.求⊙O半径的长.
27.如图所示,破残的圆形轮片上,弦AB的垂直平分线交弧AB于点C,交弦AB于点D.已知:AB=24cm,CD=8cm.
(1)求作此残片所在的圆(不写作法,保留作图痕迹).
(2)求残片所在圆的面积.
参考答案与试题解析
一.选择题
1.解:当点P是⊙O外一点时,OP>5cm,A、B、C均不符.
故选:D.
2.解:如图所示,连接OD.
∵弦CD⊥AB,AB为圆O的直径,
∴E为CD的中点,
又∵CD=16,
∴CE=DE=CD=8,
又∵OD=AB=10,
∵CD⊥AB,
∴∠OED=90°,
在Rt△ODE中,DE=8,OD=10,
根据勾股定理得:OE2+DE2=OD2,
∴OE==6,
则OE的长度为6,
故选:C.
3.解:EF的中点M,作MN⊥AD于点M,取MN上的球心O,连接OF,
∵四边形ABCD是矩形,
∴∠C=∠D=90°,
∴四边形CDMN是矩形,
∴MN=CD=4,
设OF=x,则ON=OF,
∴OM=MN﹣ON=4﹣x,MF=2,
在直角三角形OMF中,OM2+MF2=OF2
即:(4﹣x)2+22=x2
解得:x=2.5
故选:B.
4.解:A、根据两点确定一条直线可知说法错误;
B、两点可以确定两条直线,故说法错误;
C、不在同一直线上的三点确定一个圆,故说法错误;
D、正确;
故选:D.
5.解:A、在同一平面上但不在同一条直线上的三点确定一个圆,故选项错误;
B、三角形的外心是三边垂直平分线的交点,它到三角形各顶点的距离相等,故选项正确;
C、同圆或等圆中,相等的圆心角所对的弧相等,故选项正确;
D、经过切点且垂直于切线的直线必经过圆心,故选项正确.
故选:A.
6.解:若AB是⊙O的直径时,AB=2r.
若AB不是⊙O的直径时,AB<2r,无法判定AB与r的大小关系.
观察选项,选项D符合题意.
故选:D.
7.解:分别作OD⊥AB,OE⊥AC,垂足分别是D、E.
∵OE⊥AC,OD⊥AB,
∴AE=AC=,AD=AB=1,
∴sin∠AOE==,sin∠AOD==,
∴∠AOE=45°,∠AOD=30°,
∴∠BAO=60°,∠CAO=90°﹣45°=45°,
∴∠BAC=45°+60°=105°,或∠BAC′=60°﹣45°=15°.
∴∠BAC=15°或105°,
故选:D.
8.解:连接OD,交AC于F,
∵D是的中点,
∴OD⊥AC,AF=CF,
∴∠DFE=90°,
∵OA=OB,AF=CF,
∴OF=BC,
∵AB是直径,
∴∠ACB=90°,
在△EFD和△ECB中
∴△EFD≌△ECB(AAS),
∴DF=BC,
∴OF=DF,
∵OD=3,
∴OF=1,
∴BC=2,
在Rt△ABC中,AC2=AB2﹣BC2,
∴AC===4,
故选:D.
9.解:因为五边形的各边长都和小圆的周长相等,所以小圆在每一边上滚动正好一周,在五条边上共滚动了5周.由于每次小圆从五边形的一边滚动到另一边时,都会翻转72°,所以小圆在五个角处共滚动一周.因此,总共是滚动了6周.
故选:C.
10.解:∵=,
∴∠AOC=∠BOC=45°,
∴∠AOB=45°+45°=90°,
故选:D.
二.填空题
11.解:∵△ABC中,∠ACB=90°,∠A=40°
∴∠B=50°
∵BC=CD
∴∠B=∠BDC=50°
∴∠BCD=80°
∴∠ACD=10°.
12.解:连接OA,OD,OM.
∵四边形ABOC、DEOF、HMON均为矩形.
∴OA=BC,OD=EF,OM=HN
∴BC=EF=HN
即a=b=c.
故答案是:a=b=c.
13.解:把最小圆的阴影部分圆点为定点顺时针旋转90°,然后把最外边的阴影部分逆时针旋转90°,即可填充满最大圆的
而最大圆的面积为π
∴答案为.
14.解:∵点P的坐标是(﹣4,3),
∴OP==5,
∵OP等于圆O的半径,
∴点P在圆O上.
故答案为点P在圆O上.
15.解:如图所示,连接OD.
∵弦CD⊥AB,AB为圆O的直径,
∴E为CD的中点,
又∵CD=16,
∴CE=DE=CD=8,
又∵OD=AB=10,
∵CD⊥AB,
∴∠OED=90°,
在Rt△ODE中,DE=8,OD=10,
根据勾股定理得:OE2+DE2=OD2,
∴OE==6,
则OE的长度为6.
16.解:如图,连接BO′,
∵A(6,0),C(﹣2,0),
∴O′C=O′A=O′B=4,OO′=4﹣2=2,
在Rt△BOO′中,由勾股定理得:OB==2,
∴B的坐标为(0,﹣2),
故答案为:(0,﹣2).
17.解:设经过A,B两点的直线解析式为y=kx+b,
由A(3,0)、B(0,﹣4),
得,
解得.
∴经过A,B两点的直线解析式为y=x﹣4;
当x=2时y=x﹣4=﹣≠﹣3,
所以点C(2,﹣3)不在直线AB上,
即A,B,C三点不在同一直线上,
因为“两点确定一条直线”,
所以A,B,C三点可以确定一个圆.
故答案为能.
18.解:设CD于AB交于G,与MN交于H,
∵CD=18m,AE=10m,AB=24m,HD=17m,
∴CG=8m,AG=12m,CH=1m,
设圆拱的半径为r,
在Rt△AOG中,OA2=OG2+AG2,
∴r2=(r﹣8)2+122,
解得r=13,
∴OC=13m,
∴OH=13﹣1=12m,
在Rt△MOH中,OM2=OH2+MH2,
∴132=122+MH2,
解得MH2=25,
∴MH=5m,
∴MN=10m,
故答案为10.
19.解:正方形的四个顶点和它的中心的点的距离相等,中心与一边的两个端点可以确定一个圆,正方形有四条边,因而有四个圆;而正方形的四个顶点都在以中心为圆心的圆上,因而能确定5个不同的圆.
20.解:如下图,连接AM,连接MB,
∵∠BAD=∠CDA=90°,
∴AM过圆心O,
而A、D、M、B四点共圆,
∴四边形ADMB为矩形,而AB=1,CD=2,
∴CM=2﹣1=1=AB=DM,即:①DM=CM,正确;
又AB∥CD,
∴四边形ABMC为平行四边形,
∴∠AEB=∠MAE,=,故②正确;
∵四边形ADMB为矩形,
∴AB=DM,
∴=,
∴∠DAM=∠AMB,
过点O作OG⊥AD于G,OH⊥AE于H,
∴OG=OH,
∴AD=AE,
∴④正确;
由题设条件求不出直径的大小,
故③⊙O的直径为2,错误;
故答案为①②④.
三.解答题
21.解:AC与BD相等.理由如下:
连接OC、OD,如图,
∵OA=OB,AE=BF,
∴OE=OF,
∵CE⊥AB,DF⊥AB,
∴∠OEC=∠OFD=90°,
在Rt△OEC和Rt△OFD中,
,
∴Rt△OEC≌Rt△OFD(HL),
∴∠COE=∠DOF,
∴=,
∴AC=BD.
22.解:∵AB、CD为⊙O中两条直径,
∴OA=OB,OC=OD,
∵CE=DF,
∴OE=OF,
在△AOF和△BOE中,
,
∴△AOF≌△BOE(SAS),
∴AF=BE.
23.证明:∵OD⊥AB,
∴AD=BD=AB.
同理AE=CE=AC.
∵AB=AC,∴AD=AE.
∵OD⊥ABOE⊥ACAB⊥AC,
∴∠OEA=∠A=∠ODA=90°,
∴四边形ADOE为矩形.
又∵AD=AE,
∴矩形ADOE为正方形.
24.解:∵OB=OC∴∠OCB=∠OBC=40°(2分)
∴∠BOC=180°﹣∠OBC﹣∠OCB=180°﹣40°﹣40°=100°(3分)
∴∠AOC=∠AOB+∠BOC=50°+100°=150°(4分)
又∵OA=OC∴∠OAC==15°(6分)
25.解;(1)连接AC,
∵AB=3cm,AD=4cm,
∴AC=5cm,
∴点B在⊙A内,点D在⊙A上,点C在⊙A外;
(2)∵以点A为圆心作⊙A,使B,C,D三点中至少有一个点在圆内,且至少有一点在圆外,
∴⊙A的半径r的取值范围是:3cm<r<5cm.
26.解:连接AO,
∵半径OC⊥弦AB,
∴AD=BD,
∵AB=12,
∴AD=BD=6,
设⊙O的半径为R,
∵CD=2,
∴OD=R﹣2,
在Rt△AOD中,OA2=OD2+AD2,即:R2=(R﹣2)2+62,
∴R=10,
答:⊙O的半径长为10.
27.解:(1)作弦AC的垂直平分线与弦AB的垂直平分线交于O点,以O为圆心OA长为半径作圆O就是此残片所在的圆,如图.
(2)连接OA,设OA=x,AD=12cm,OD=(x﹣8)cm,
则根据勾股定理列方程:
x2=122+(x﹣8)2,
解得:x=13.
即:圆的半径为13cm.
所以圆的面积为:π×132=169π(cm2).
对称图形——圆》单元测试卷
一.选择题
1.已知⊙O的半径为5cm,P为⊙O外一点,则OP的长可能是( )
A.5
cm
B.4
cm
C.3
cm
D.6
cm
2.如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=20,CD=16,那么线段OE的长为( )
A.10
B.8
C.6
D.4
3.把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=4cm,则球的半径长是( )
A.2cm
B.2.5cm
C.3cm
D.4cm
4.下列说法正确的是( )
A.一个点可以确定一条直线
B.两个点可以确定两条直线
C.三个点可以确定一个圆
D.不在同一直线上的三点确定一个圆
5.下列命题错误的是( )
A.经过三个点一定可以作圆
B.三角形的外心到三角形各顶点的距离相等
C.同圆或等圆中,相等的圆心角所对的弧相等
D.经过切点且垂直于切线的直线必经过圆心
6.已知AB是⊙O的弦,⊙O的半径为r,下列关系式一定成立的是( )
A.AB>r
B.AB<r
C.AB<2r
D.AB≤2r
7.半径为2的圆中,弦AB、AC的长分别2和2,则∠BAC的度数是( )
A.15°
B.15°或45°
C.15°或75°
D.15°或105°
8.如图,在半径为3的⊙O中,AB是直径,AC是弦,D是的中点,AC与BD交于点E.若E是BD的中点,则AC的长是( )
A.
B.3
C.3
D.4
9.如图,一个小圆沿着一个五边形的边滚动,如果五边形的各边长都和小圆的周长相等,那么当小圆滚动到原来位置时,小圆自身滚动的圈数是( )
A.4
B.5
C.6
D.10
10.如图在⊙O中,若点C是的中点,∠AOC=45°,则∠AOB=( )
A.45°
B.80°
C.85°
D.90°
二.填空题
11.如图,△ABC中,∠ACB=90°,∠A=40°,以C为圆心、CB为半径的圆交AB于点D,则∠ACD=
度.
12.如图,点A、D、G、M在半圆O上,四边形ABOC、DEOF、HMNO均为矩形,设BC=a,EF=b,NH=c,则a、b、c的大小是
.
13.如图所示的三个圆是同心圆,那么图中阴影部分的面积为
.(结果保留π)
14.若圆O的半径是5,圆心的坐标是(0,0),点P的坐标是(﹣4,3),则点P与⊙O的位置关系是
.
15.如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=20,CD=16,那么线段OE的长为
.
16.如图,在平面直角坐标系中,⊙Oˊ与两坐标轴分别交于A、B、C、D四点,已知A(6,0),C(﹣2,0).则点B的坐标为
.
17.根据“不在同一直线上的三点确定一个圆”,可以判断平面直角坐标系内的三个点A(3,0)、B(0,﹣4)、C(2,﹣3)
确定一个圆(填“能”或“不能”).
18.某公路上有一隧道,顶部是圆弧形拱顶,圆心为O,隧道的水平宽AB为24m,AB离地面的高度AE=10
m,拱顶最高处C离地面的高度CD为18m,在拱顶的M,N处安装照明灯,且M,N离地面的高度相等都等于17m,则MN=
m.
19.正方形的四个顶点和它的中心共5个点能确定
个不同的圆.
20.如图,在四边形ABCD中,∠BAD=∠CDA=90°,AB=1,CD=2,过A,B,D三点的⊙O分别交BC,CD于点E,M,下列结论:①DM=CM;②;③⊙O的直径为2;④AE=AD.其中正确的结论有
(填序号).
三.解答题
21.已知:如图,AB是⊙O的直径,点C、D在⊙O上,CE⊥AB于E,DF⊥AB于F,且AE=BF,AC与BD相等吗?为什么?
22.如图,AB、CD为⊙O中两条直径,点E、F在直径CD上,且CE=DF.
求证:AF=BE.
23.如图,在⊙O中,AB、AC为互相垂直且相等的两条弦,OD⊥AB于D,OE⊥AC于E.求证:四边形AEOD是正方形.
24.如图:A、B、C是⊙O上的三点,∠AOB=50°,∠OBC=40°,求∠OAC的度数.
25.如图所示,已知矩形ABCD的边AB=3cm,AD=4cm.
(1)以点A为圆心,4cm为半径作⊙A,则点B,C,D与⊙A的位置关系如何?
(2)若以点A为圆心作⊙A,使B,C,D三点中至少有一个点在圆内,且至少有一点在圆外,则⊙A的半径r的取值范围是什么?
26.如图,在⊙O中,半径OC⊥弦AB,垂足为点D,AB=12,CD=2.求⊙O半径的长.
27.如图所示,破残的圆形轮片上,弦AB的垂直平分线交弧AB于点C,交弦AB于点D.已知:AB=24cm,CD=8cm.
(1)求作此残片所在的圆(不写作法,保留作图痕迹).
(2)求残片所在圆的面积.
参考答案与试题解析
一.选择题
1.解:当点P是⊙O外一点时,OP>5cm,A、B、C均不符.
故选:D.
2.解:如图所示,连接OD.
∵弦CD⊥AB,AB为圆O的直径,
∴E为CD的中点,
又∵CD=16,
∴CE=DE=CD=8,
又∵OD=AB=10,
∵CD⊥AB,
∴∠OED=90°,
在Rt△ODE中,DE=8,OD=10,
根据勾股定理得:OE2+DE2=OD2,
∴OE==6,
则OE的长度为6,
故选:C.
3.解:EF的中点M,作MN⊥AD于点M,取MN上的球心O,连接OF,
∵四边形ABCD是矩形,
∴∠C=∠D=90°,
∴四边形CDMN是矩形,
∴MN=CD=4,
设OF=x,则ON=OF,
∴OM=MN﹣ON=4﹣x,MF=2,
在直角三角形OMF中,OM2+MF2=OF2
即:(4﹣x)2+22=x2
解得:x=2.5
故选:B.
4.解:A、根据两点确定一条直线可知说法错误;
B、两点可以确定两条直线,故说法错误;
C、不在同一直线上的三点确定一个圆,故说法错误;
D、正确;
故选:D.
5.解:A、在同一平面上但不在同一条直线上的三点确定一个圆,故选项错误;
B、三角形的外心是三边垂直平分线的交点,它到三角形各顶点的距离相等,故选项正确;
C、同圆或等圆中,相等的圆心角所对的弧相等,故选项正确;
D、经过切点且垂直于切线的直线必经过圆心,故选项正确.
故选:A.
6.解:若AB是⊙O的直径时,AB=2r.
若AB不是⊙O的直径时,AB<2r,无法判定AB与r的大小关系.
观察选项,选项D符合题意.
故选:D.
7.解:分别作OD⊥AB,OE⊥AC,垂足分别是D、E.
∵OE⊥AC,OD⊥AB,
∴AE=AC=,AD=AB=1,
∴sin∠AOE==,sin∠AOD==,
∴∠AOE=45°,∠AOD=30°,
∴∠BAO=60°,∠CAO=90°﹣45°=45°,
∴∠BAC=45°+60°=105°,或∠BAC′=60°﹣45°=15°.
∴∠BAC=15°或105°,
故选:D.
8.解:连接OD,交AC于F,
∵D是的中点,
∴OD⊥AC,AF=CF,
∴∠DFE=90°,
∵OA=OB,AF=CF,
∴OF=BC,
∵AB是直径,
∴∠ACB=90°,
在△EFD和△ECB中
∴△EFD≌△ECB(AAS),
∴DF=BC,
∴OF=DF,
∵OD=3,
∴OF=1,
∴BC=2,
在Rt△ABC中,AC2=AB2﹣BC2,
∴AC===4,
故选:D.
9.解:因为五边形的各边长都和小圆的周长相等,所以小圆在每一边上滚动正好一周,在五条边上共滚动了5周.由于每次小圆从五边形的一边滚动到另一边时,都会翻转72°,所以小圆在五个角处共滚动一周.因此,总共是滚动了6周.
故选:C.
10.解:∵=,
∴∠AOC=∠BOC=45°,
∴∠AOB=45°+45°=90°,
故选:D.
二.填空题
11.解:∵△ABC中,∠ACB=90°,∠A=40°
∴∠B=50°
∵BC=CD
∴∠B=∠BDC=50°
∴∠BCD=80°
∴∠ACD=10°.
12.解:连接OA,OD,OM.
∵四边形ABOC、DEOF、HMON均为矩形.
∴OA=BC,OD=EF,OM=HN
∴BC=EF=HN
即a=b=c.
故答案是:a=b=c.
13.解:把最小圆的阴影部分圆点为定点顺时针旋转90°,然后把最外边的阴影部分逆时针旋转90°,即可填充满最大圆的
而最大圆的面积为π
∴答案为.
14.解:∵点P的坐标是(﹣4,3),
∴OP==5,
∵OP等于圆O的半径,
∴点P在圆O上.
故答案为点P在圆O上.
15.解:如图所示,连接OD.
∵弦CD⊥AB,AB为圆O的直径,
∴E为CD的中点,
又∵CD=16,
∴CE=DE=CD=8,
又∵OD=AB=10,
∵CD⊥AB,
∴∠OED=90°,
在Rt△ODE中,DE=8,OD=10,
根据勾股定理得:OE2+DE2=OD2,
∴OE==6,
则OE的长度为6.
16.解:如图,连接BO′,
∵A(6,0),C(﹣2,0),
∴O′C=O′A=O′B=4,OO′=4﹣2=2,
在Rt△BOO′中,由勾股定理得:OB==2,
∴B的坐标为(0,﹣2),
故答案为:(0,﹣2).
17.解:设经过A,B两点的直线解析式为y=kx+b,
由A(3,0)、B(0,﹣4),
得,
解得.
∴经过A,B两点的直线解析式为y=x﹣4;
当x=2时y=x﹣4=﹣≠﹣3,
所以点C(2,﹣3)不在直线AB上,
即A,B,C三点不在同一直线上,
因为“两点确定一条直线”,
所以A,B,C三点可以确定一个圆.
故答案为能.
18.解:设CD于AB交于G,与MN交于H,
∵CD=18m,AE=10m,AB=24m,HD=17m,
∴CG=8m,AG=12m,CH=1m,
设圆拱的半径为r,
在Rt△AOG中,OA2=OG2+AG2,
∴r2=(r﹣8)2+122,
解得r=13,
∴OC=13m,
∴OH=13﹣1=12m,
在Rt△MOH中,OM2=OH2+MH2,
∴132=122+MH2,
解得MH2=25,
∴MH=5m,
∴MN=10m,
故答案为10.
19.解:正方形的四个顶点和它的中心的点的距离相等,中心与一边的两个端点可以确定一个圆,正方形有四条边,因而有四个圆;而正方形的四个顶点都在以中心为圆心的圆上,因而能确定5个不同的圆.
20.解:如下图,连接AM,连接MB,
∵∠BAD=∠CDA=90°,
∴AM过圆心O,
而A、D、M、B四点共圆,
∴四边形ADMB为矩形,而AB=1,CD=2,
∴CM=2﹣1=1=AB=DM,即:①DM=CM,正确;
又AB∥CD,
∴四边形ABMC为平行四边形,
∴∠AEB=∠MAE,=,故②正确;
∵四边形ADMB为矩形,
∴AB=DM,
∴=,
∴∠DAM=∠AMB,
过点O作OG⊥AD于G,OH⊥AE于H,
∴OG=OH,
∴AD=AE,
∴④正确;
由题设条件求不出直径的大小,
故③⊙O的直径为2,错误;
故答案为①②④.
三.解答题
21.解:AC与BD相等.理由如下:
连接OC、OD,如图,
∵OA=OB,AE=BF,
∴OE=OF,
∵CE⊥AB,DF⊥AB,
∴∠OEC=∠OFD=90°,
在Rt△OEC和Rt△OFD中,
,
∴Rt△OEC≌Rt△OFD(HL),
∴∠COE=∠DOF,
∴=,
∴AC=BD.
22.解:∵AB、CD为⊙O中两条直径,
∴OA=OB,OC=OD,
∵CE=DF,
∴OE=OF,
在△AOF和△BOE中,
,
∴△AOF≌△BOE(SAS),
∴AF=BE.
23.证明:∵OD⊥AB,
∴AD=BD=AB.
同理AE=CE=AC.
∵AB=AC,∴AD=AE.
∵OD⊥ABOE⊥ACAB⊥AC,
∴∠OEA=∠A=∠ODA=90°,
∴四边形ADOE为矩形.
又∵AD=AE,
∴矩形ADOE为正方形.
24.解:∵OB=OC∴∠OCB=∠OBC=40°(2分)
∴∠BOC=180°﹣∠OBC﹣∠OCB=180°﹣40°﹣40°=100°(3分)
∴∠AOC=∠AOB+∠BOC=50°+100°=150°(4分)
又∵OA=OC∴∠OAC==15°(6分)
25.解;(1)连接AC,
∵AB=3cm,AD=4cm,
∴AC=5cm,
∴点B在⊙A内,点D在⊙A上,点C在⊙A外;
(2)∵以点A为圆心作⊙A,使B,C,D三点中至少有一个点在圆内,且至少有一点在圆外,
∴⊙A的半径r的取值范围是:3cm<r<5cm.
26.解:连接AO,
∵半径OC⊥弦AB,
∴AD=BD,
∵AB=12,
∴AD=BD=6,
设⊙O的半径为R,
∵CD=2,
∴OD=R﹣2,
在Rt△AOD中,OA2=OD2+AD2,即:R2=(R﹣2)2+62,
∴R=10,
答:⊙O的半径长为10.
27.解:(1)作弦AC的垂直平分线与弦AB的垂直平分线交于O点,以O为圆心OA长为半径作圆O就是此残片所在的圆,如图.
(2)连接OA,设OA=x,AD=12cm,OD=(x﹣8)cm,
则根据勾股定理列方程:
x2=122+(x﹣8)2,
解得:x=13.
即:圆的半径为13cm.
所以圆的面积为:π×132=169π(cm2).
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
