3 1 2椭圆的几何性质(备课件)【16张】-2021-2022学年高二数学同步备课系列(苏教版2019选择性必修第一册)
文档属性
| 名称 | 3 1 2椭圆的几何性质(备课件)【16张】-2021-2022学年高二数学同步备课系列(苏教版2019选择性必修第一册) |  | |
| 格式 | pptx | ||
| 文件大小 | 454.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-14 09:21:13 | ||
图片预览





文档简介
3.1.2椭圆的几何性质
学习目标
1.理解椭圆的简单几何性质,掌握长轴、短轴、离心率、等基本概念.
2.掌握椭圆的几何图形和相应几何性质.
复习引入
1.椭圆的定义
——————————————
2.椭圆的标准方程:
焦点所在轴
焦点在x轴
焦点在y轴
图形
标准方程
焦点坐标
a,b,c的关系
x
y
o
x
y
o
a2=b2+c2
(±c, 0)
(0, ±c)
|MF1|+|MF2|=2a
(2a>|F1F2|)
复习引入
1.方程4x2+25y2=100表示什么样的曲线?
2.你认为要画出第1题的图形时要考虑哪些因素?
范围大小
对称性
特殊点位置
圆扁情况
合作探究
o
x
y
-a≤x≤a , -b ≤y≤b
一、椭圆的范围
?
这说明椭圆位于直线x=±a和y=±b所围成的矩形框里
y
x
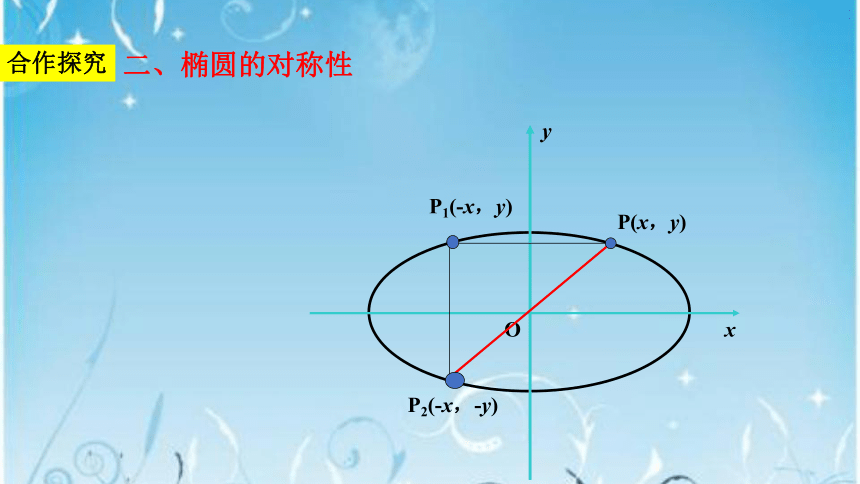
O
P(x,y)
P1(-x,y)
P2(-x,-y)
二、椭圆的对称性
合作探究
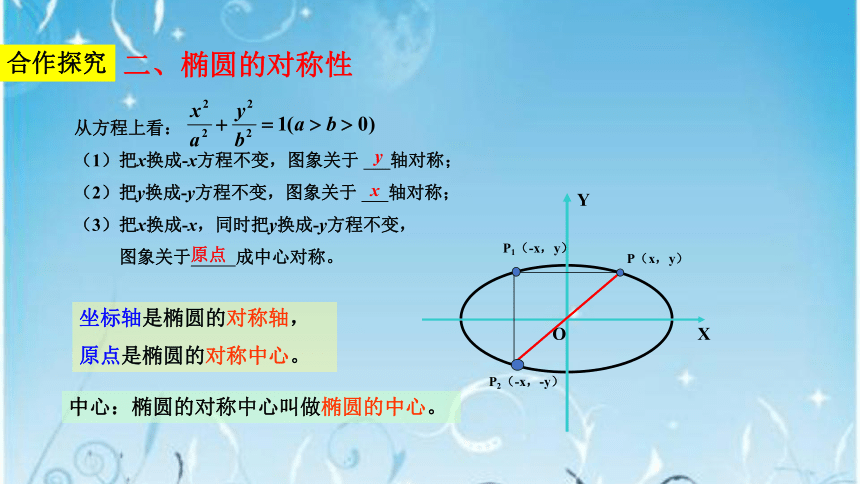
从方程上看:
(1)把x换成-x方程不变,图象关于 轴对称;
(2)把y换成-y方程不变,图象关于 轴对称;
(3)把x换成-x,同时把y换成-y方程不变,
图象关于 成中心对称。
y
x
原点
坐标轴是椭圆的对称轴,
原点是椭圆的对称中心。
中心:椭圆的对称中心叫做椭圆的中心。
Y
X
O
P(x,y)
P1(-x,y)
P2(-x,-y)
二、椭圆的对称性
合作探究
合作探究
长轴长=_______ 长半轴长=________
短轴长=_______ 短半轴长=________
o
F1
F2
B2
B1
A1
A2
顶点
(-a,0)
(a,0)
(0, -b)
(0, b)
长轴
短轴
填一填
2a
a
2b
b
三、椭圆上特殊的点
数学应用
活动:画出这两个椭圆的图像
y
x
O
y
x
O
(5,0)
(0,-3)
(-5,0)
(0,3)
(5,0)
(0,-4)
(-5,0)
(0,4)
数学应用
由椭圆的范围、对称性和顶点,
再进行描点画图,只须描出较少的
点,就可以得到较正确的图形.
小 结 :
活动:画出这两个椭圆的图像
y
x
O
y
x
O
(5,0)
(0,-3)
(-5,0)
(0,3)
(5,0)
(0,-4)
(-5,0)
(0,4)
哪个更圆?扁平的程度由哪些数据决定的?
合作探究
活动:讨论椭圆在下列条件下,椭圆将会怎样变化
1、a不变,b变大 2、a不变,b变小
3、b不变,a变大 4、b不变,a变小
y
x
O
(a,0)
(0,-b)
(-a,0)
(0,b)
(0,-4)
合作探究
数学建构
方程
图形
范围
对称性
顶点
离心率
x
y
O
x
y
O
数学应用
例1 椭圆的一个顶点为 ,其长轴长是短轴长的2倍,求椭圆的标准方程.
分析:题目没有指出焦点的位置,要考虑两种位置
椭圆的标准方程为: ;
椭圆的标准方程为: ;
解:(1)当 为长轴端点时, , ,
(2)当 为短轴端点时, , ,
综上所述,椭圆的标准方程是 或
数学应用
例2 已知椭圆 的离心率 ,求 的值
由 ,得:
解:当椭圆的焦点在 轴上时,
, ,得 .
当椭圆的焦点在 轴上时,
, ,得 .
由 ,得 ,即 .
∴满足条件的 或 .
达标测试
1、求适合下列条件的椭圆的标准方程:
2、求适合下列条件的椭圆的标准方程:
(1)经过点P(-3,0)、Q(0,-2);
(2)长轴的长等于20,离心率等于 .
谢谢!
学习目标
1.理解椭圆的简单几何性质,掌握长轴、短轴、离心率、等基本概念.
2.掌握椭圆的几何图形和相应几何性质.
复习引入
1.椭圆的定义
——————————————
2.椭圆的标准方程:
焦点所在轴
焦点在x轴
焦点在y轴
图形
标准方程
焦点坐标
a,b,c的关系
x
y
o
x
y
o
a2=b2+c2
(±c, 0)
(0, ±c)
|MF1|+|MF2|=2a
(2a>|F1F2|)
复习引入
1.方程4x2+25y2=100表示什么样的曲线?
2.你认为要画出第1题的图形时要考虑哪些因素?
范围大小
对称性
特殊点位置
圆扁情况
合作探究
o
x
y
-a≤x≤a , -b ≤y≤b
一、椭圆的范围
?
这说明椭圆位于直线x=±a和y=±b所围成的矩形框里
y
x
O
P(x,y)
P1(-x,y)
P2(-x,-y)
二、椭圆的对称性
合作探究
从方程上看:
(1)把x换成-x方程不变,图象关于 轴对称;
(2)把y换成-y方程不变,图象关于 轴对称;
(3)把x换成-x,同时把y换成-y方程不变,
图象关于 成中心对称。
y
x
原点
坐标轴是椭圆的对称轴,
原点是椭圆的对称中心。
中心:椭圆的对称中心叫做椭圆的中心。
Y
X
O
P(x,y)
P1(-x,y)
P2(-x,-y)
二、椭圆的对称性
合作探究
合作探究
长轴长=_______ 长半轴长=________
短轴长=_______ 短半轴长=________
o
F1
F2
B2
B1
A1
A2
顶点
(-a,0)
(a,0)
(0, -b)
(0, b)
长轴
短轴
填一填
2a
a
2b
b
三、椭圆上特殊的点
数学应用
活动:画出这两个椭圆的图像
y
x
O
y
x
O
(5,0)
(0,-3)
(-5,0)
(0,3)
(5,0)
(0,-4)
(-5,0)
(0,4)
数学应用
由椭圆的范围、对称性和顶点,
再进行描点画图,只须描出较少的
点,就可以得到较正确的图形.
小 结 :
活动:画出这两个椭圆的图像
y
x
O
y
x
O
(5,0)
(0,-3)
(-5,0)
(0,3)
(5,0)
(0,-4)
(-5,0)
(0,4)
哪个更圆?扁平的程度由哪些数据决定的?
合作探究
活动:讨论椭圆在下列条件下,椭圆将会怎样变化
1、a不变,b变大 2、a不变,b变小
3、b不变,a变大 4、b不变,a变小
y
x
O
(a,0)
(0,-b)
(-a,0)
(0,b)
(0,-4)
合作探究
数学建构
方程
图形
范围
对称性
顶点
离心率
x
y
O
x
y
O
数学应用
例1 椭圆的一个顶点为 ,其长轴长是短轴长的2倍,求椭圆的标准方程.
分析:题目没有指出焦点的位置,要考虑两种位置
椭圆的标准方程为: ;
椭圆的标准方程为: ;
解:(1)当 为长轴端点时, , ,
(2)当 为短轴端点时, , ,
综上所述,椭圆的标准方程是 或
数学应用
例2 已知椭圆 的离心率 ,求 的值
由 ,得:
解:当椭圆的焦点在 轴上时,
, ,得 .
当椭圆的焦点在 轴上时,
, ,得 .
由 ,得 ,即 .
∴满足条件的 或 .
达标测试
1、求适合下列条件的椭圆的标准方程:
2、求适合下列条件的椭圆的标准方程:
(1)经过点P(-3,0)、Q(0,-2);
(2)长轴的长等于20,离心率等于 .
谢谢!
