七年级数学《平行线》导学案
文档属性
| 名称 | 七年级数学《平行线》导学案 |

|
|
| 格式 | zip | ||
| 文件大小 | 63.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-06-02 18:37:45 | ||
图片预览




文档简介
《平行线》导学案
□ 自学导读·领悟知识我能行
【学习目标】1、了解平行线的概念,理解同一平面内两条直线间的位置关系;
2、掌握平行公理及平行线的画法。
【学习重点】平行线的概念、画法及平行公理。
【学习难点】解平行线的概念和根据几何语言画出图形。
【读书思考】1、什么是平行线?“平行”用什么表示?
2、平面内两条直线的位置关系有哪些?
3、平行公理及推论是什么?
【归纳小结】
知识点一、平行线定义
(1)用数学语言描述平行定义: 同一平面内,存在一条直线a与直线b不相交的位置,这时直线a与b互相平行.换言之,同一平面内, ________________叫做平行线.
(2)平行线表示法:
直线a与b是平行线,记作“∥”,这里“∥”是平行符号.
(3)在同一平面内,两条直线位置关系:
______或_______,两者必居其一.即两条直线___________________.
知识点二、平行公理及推论.
(1) 对照垂线的第一性质说出画图所得的结论.
(2) 在学生充分交流后,,归纳。
平行公理:_____________________________________________________.
(3) 比较平行公理和垂线的第一条性质.
共同点:都是“有且只有一条直线”,这表明与已知直线平行或垂直的直线存在并且是唯一的.
不同点:平行公理中所过的“一点”要在已知直线外,两垂线性质中对“一点”没有限制,可在直线上,也可在直线外.
(4) 归纳平行公理推论_____________________________________________________.
.【典题解析】
例1、判断下列说法是否正确?
(1)在同一平面内,两条线段不相交就平行;
(2)在同一平面内,平行于直线AB的直线只有一条。
(3)如果几条直线都和同一条直线平行,那么这几条直线都互相平行。
例2.读下列语句,并画出图形后判断.
(1)直线a、b互相垂直,点P是直线a、b外一点,过P点的直线c垂直于直线b.
(2)判断直线a、c的位置关系,并借助于三角尺、直尺验证.
例3.试说明三条直线的交点情况,进而判定在同一平面内三条直线的位置情况.
基础训练·基本题型我过关。
1、下列说法中错误的有( )个。
(1)两条不相交的直线叫做平行线
(2)经过直线外一点,能够画出一条直线与已知直线平行,并且只能画出一条
(3)如果a//b,b//c,则b//c (4)两条不平行的射线,在同一平面内一定相交
A、0 B、1 C、2 D、3
2、直线为空间内的两条直线,它们的位置关系是( )
A、平行 B、相交 C、异面 D、平行、相交或异面
3、在同一平面内的三条直线,如果要使其中两条且只有两条平行,那么它们( )
A、有三个交点 B、只有一个交点 C、有两个交点 D、没有交点
4、在同一平面内,直线相交于点O,且,则直线和的关系是( )
A、平行 B、相交 C、重合 D、以上都有可能
5、两条射线平行是指( )
A、两条射线都是水平的 B、两条射线都在同一直线上且方向相同
C、两条射线方向相反 D、两条射线所在直线平行
□ 能力提升·走进中考我能赢
1、在平面内有两两相交的3条直线,如果最多有个交点,最少有个交点,那么=( )
A、0 B、1 C、3 D、6
2、作图:在梯形ABCD中,上底、下底分别为AD、BC,点M为AB中点,
(1)过M点作MN//AD交CD于N A D
(2)MN和BC平行吗?为什么?
(3)用适当的方法度量并比较NC和ND的大小关系 M
B C
《5.2.1 平行线》补偿训练
(检测时间45分钟 满分100分)
班级_____________________ 姓名_______________得分_____
一、选择题:(每小题4分,共20分)
1.在同一平面内,两条不重合直线的位置关系可能是( )毛
A.平行或相交 B.垂直或相交; C.垂直或平行 D.平行、垂直或相交
2.下列说法正确的是( )
A.经过一点有一条直线与已知直线平行
B.经过一点有无数条直线与已知直线平行
C.经过一点有且只有一条直线与已知直线平行
D.经过直线外一点有且只有一条直线与已知直线平行
3.在同一平面内有三条直线,若其中有两条且只有两条直线平行,则它们交点的 个数为( )
A.0个 B.1个 C.2个 D.3个
4.下列说法正确的有( )
①不相交的两条直线是平行线;②在同一平面内,两条直线的位置关系有两种;
③若线段AB与CD没有交点,则AB∥CD;④若a∥b,b∥c,则a与c不相交.
A.1个 B.2个 C.3个 D.4个
5.过一点画已知直线的平行线,则( )
A.有且只有一条 B.有两条; C.不存在 D.不存在或只有一条
二、填空题:(每小题4分,共20分)
1.在同一平面内,____________________________________叫做平行线.
2.若AB∥CD,AB∥EF,则_____∥______,理由是__________________.
3.在同一平面内,若两条直线相交,则公共点的个数是________;若两条直线平 行,则公共点的个数是_________.
4.同一平面内的三条直线,其交点的个数可能为________.
5.直线L同侧有A,B,C三点,若过A,B的直线L1和过B,C的直线L2都与L平行,则A, B,C三点________,理论根据是___________________________.
三、解答题:(每小题12分,共48分)
已知直线a∥b,b∥c,c∥d,则a与d的关系是什么 为什么
2.如图所示,梯形ABCD中,AD∥BC,P是AB的中点,过P点作AD的平行线交DC于Q点.
(1)PQ与BC平行吗 为什么
(2)测量PQ与CQ的长,DQ与CQ是否相等
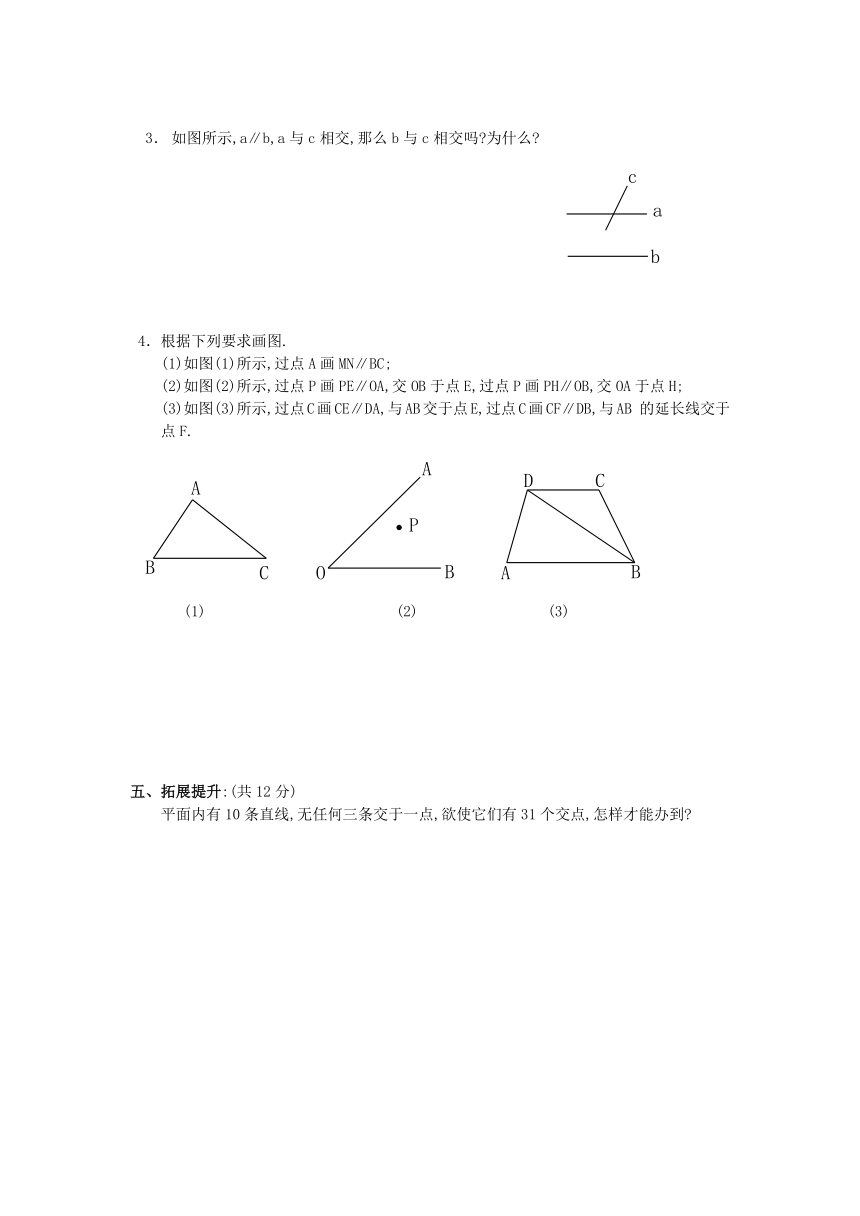
如图所示,a∥b,a与c相交,那么b与c相交吗 为什么
4.根据下列要求画图.
(1)如图(1)所示,过点A画MN∥BC;
(2)如图(2)所示,过点P画PE∥OA,交OB于点E,过点P画PH∥OB,交OA于点H;
(3)如图(3)所示,过点C画CE∥DA,与AB交于点E,过点C画CF∥DB,与AB的延长线交 于点F.
(1) (2) (3)
五、拓展提升:(共12分)
平面内有10条直线,无任何三条交于一点,欲使它们有31个交点,怎样才能办到
5.2.2 平行线的判定(第1课时)
□ 自学导读·领悟知识我能行
【学习目标】经历探索两直线平行条件的过程,理解两直线平行的条件.
【学习重点】探索两直线平行的条件。
【学习难点】理解“同位角相等,两条直线平行”。
【读书思考】
1如图(课本13面图5.2-5)在三角板移动的过程中,什么没有变?三角板经过点P的边与靠在直尺上的边所成的角没有变 。
2怎样判断两条直线平行?
【温故知新】
1. 判断:两条直线被第三条直线所截,如果同位角相等,那么内错角也相等.( )
2. 判断:两条直线被第三条直线所截,如果内错角互补,那么同旁内角相等.( )
3、在图1中,与∠1是同位角的是 ,与∠2是内错角的是 ,与∠A是同旁内角的是 。
4、如图2,∠5和∠7是 ,∠4和∠6是 ,∠1和∠5是 ,∠2与∠6是 ,∠1和∠3是 ,∠5和∠6是 。
5、如图3,∠ADC和∠BCD是直线 、 被直线 所截得到的 角;∠1和∠5是直线 、 被直线 所截得到的 角;∠4和∠9是直线 、 被直线 所截得到的 角;∠2和∠3是直线 、 被直线 所截得到的 角;
图1 图2 图3
【归纳小结】
知识点一、直线平行的条件
如图(课本13面图5.2-5)在三角板移动的过程中,什么没有变?三角板经过点P的边与靠在直尺上的边所成的角没有变 。
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单地说:同位角相等,两条直线平行.
符号语言: ∵∠1=∠2 ∴AB∥CD.
知识点二、
如图(课本14面5.2-7),你能说出木工用图中这种叫做角尺的工具画平行线的道理吗?
用角尺画平行线,实际上是画出了两个直角,根据“同位角相等,两条直线平行.”,可知这样画出的就是平行线。
如图,(1)如果∠2=∠3,能得出a∥b吗?(2)如果∠2+∠4=1800,能得出a∥b吗?
你能用文字语言概括上面的结论吗?
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简单地说:内错角相等,两直线平行.
符号语言:∵∠2=∠3 ∴a∥b.
(2)∵ ∠4+∠2=180°,∠4+∠1=180° (已知)
∴∠2=∠1 (同角的补角相等)
∴a∥b. (同位角相等,两条直线平行)
你能用文字语言概括上面的结论吗?
两条直线被第三条直线所截,如果同旁内角互补,那么两条直线平行.
简单地说:同旁内角互补,两直线平行
.符号语言: ∵∠4+∠2=180° ∴ a∥b.
【典题解析】
例1.右图,由图和已知条件,下列判断中正确的是( )
A.由∠1=∠6,得AB∥FG;
B.由∠1+∠2=∠6+∠7,得CE∥EI
C.由∠1+∠2+∠3+∠5=180°,得CE∥FI;
D.由∠5=∠4,得AB∥FG
2、已知直线a、b被直线c所截,且∠1+∠2=180°,试判断直线a、b的位置关系,并说明理由.
基础训练·基本题型我过关。
1.如图1,如果∠3=∠7,或______,那么______,理由是__________;如果∠5=∠3,或笔________,那么________, 理由是______________; 如果∠2+ ∠5= ______ 或者_______,那么a∥b,理由是__________.
(1) (2) (3)
2.如图2,若∠2=∠6,则______∥_______,如果∠3+∠4+∠5+∠6=180°, 那么____∥_______,如果∠9=_____,那么AD∥BC;如果∠9=_____,那么AB∥CD.
3.如图3所示,下列条件中,不能判定AB∥CD的是( )
A.AB∥EF,CD∥EF B.∠5=∠A; C.∠ABC+∠BCD=180° D.∠2=∠3
□ 能力提升·走进中考我能赢
1、如图,下列说法一定正确的是( )
A、∠1和∠4是同位角 B、∠2和∠3是内错角
C、∠3和∠4是同旁内角 D、∠5和∠6是同位角
2、在图7中,如果∠1与∠2、∠3与∠4、∠2与∠5分别互补,那么( )
A、 B、 C、 D、
图7
3、如图8,NO、QO分别是∠ONM和∠PQN的平分线,且∠QON=90°,那么MN与PQ( )
A、可能平行也可能相交 B、一定平行 C、一定相交 D、以上答案都不对
2.2 平行线的判定(第2课时)
□ 自学导读·领悟知识我能行
【学习目标】.经历分析题意,说理过程,能灵活地选用直线平行的规定方法进行说理。
【学习重点】直线平行的条件的应用
【学习难点】选取适当判定直线平行的方法进行说理是难点.
【读书思考】(课本17-18面)垂直总与直角联系在一起,我们学过哪些判断两条直线平行的方法?
【温故知新】
1.回忆怎样用移动三角尺的方法画两条平行线的, 其中直尺和三角尺的作用是什么
2.教师提出问题:学行线后,大家还能想出过一点画一条直线的平行线的新方法吗
3.下列说法错误的是 ( )
A.同位角不一定相等 B.内错角都相等 C.同旁内角可能相等 D.同旁内角互补,两直线平行
4.不相邻的两个直角,如果它们有一边在同一直线上,那么另一边相互 ( )
A.平行 B.垂直 C.平行或垂直 D.平行或垂直或相交
5.点A在直线外,直线AB⊥,直线AC⊥,那么直线AB、AC的关系是 。
【归纳小结】
知识点 判断两直线平行的方法
(1)平行线的定义:在同一平面内不相交的两条直线平行。
(2)平行公理的推论:如果两条直线都平行于第三条直线,那么这两条直线也互相平行。
(3)两直线平行的条件:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
【典题解析】
例1:在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行吗 为什么
请同学们写出多种证明方法:
例2 如图,点B在DC上,BE平分∠ABD,∠DBE=∠A,则BE∥AC,请说明理由。
分析:由BE平分∠ABD我们可以知道什么?联系∠DBE=∠A,我们又可以知道什么?由此能得出BE∥AC吗?为什么?
解:∵BE平分∠ABD
∴∠ABE=∠DBE(角平分线的定义)
又∠DBE=∠A
∴∠ABE=∠A(等量代换)
∴BE∥AC(内错角相等,两直线平行)
注意:用符号语言书写证明过程时,要步步有据。
基础训练·基本题型我过关。
1.如图,点E在CD上,点F在BA上,G是AD延长线上一点.
(1)若∠A=∠1,则可判断_______∥_______,因为________.
(2)若∠1=∠_________,则可判断AG∥BC,因为_________.
(3)若∠2+∠________=180°,则可判断CD∥AB,因为_______
___________________. (第1题)
2.如图,一个合格的变形管道ABCD需要AB边与CD边平行,若一个拐角∠ABC=72°,则另一个拐角∠BCD=_______时,这个管道符合要求.
( (第2题)
3.如图,下列判断不正确的是( )
A.因为∠1=∠4,所以DE∥AB
B.因为∠2=∠3,所以AB∥EC
C.因为∠5=∠A,所以AB∥DE
D.因为∠ADE+∠BED=180°,所以AD∥BE
4.如图,直线AB、CD被直线EF所截,使∠1=∠2≠90°,则( )
A.∠2=∠4 B.∠1=∠4
C.∠2=∠3 D.∠3=∠4
□ 能力提升·走进中考我能赢
1、在图10中有多少个角,找出这些角的内错角和同旁内角。
2.已知,如图2,点B在AC上,BD⊥BE,∠1+∠C=90°,问射线CF与BD平行吗 试用两种方法说明理由.
5.2.2 平行线的判定补偿训练
(检测时间45分钟 满分100分)
班级_____________________ 姓名_______________得分_____
一、选择题:(每小题3分,共18分)
1.如图1所示,下列条件中,能判断AB∥CD的是( )毛
A.∠BAD=∠BCD B.∠1=∠2; C.∠3=∠4 D.∠BAC=∠ACD
(1) (2) (3)
2.如图2所示,如果∠D=∠EFC,那么( )
A.AD∥BC B.EF∥BC C.AB∥DC D.AD∥EF
3.如图3所示,能判断AB∥CE的条件是( )
A.∠A=∠ACE B.∠A=∠ECD C.∠B=∠BCA D.∠B=∠ACE
4.下列说法错误的是( )
A.同位角不一定相等 B.内错角都相等 C.同旁内角可能相等 D.同旁内角互补,两直线平行
5.不相邻的两个直角,如果它们有一边在同一直线上,那么另一边相互( )
A.平行 B.垂直 C.平行或垂直 D.平行或垂直或相交
6.如图,DM是AD的延长线,若∠MDC=∠C,则( )
A、DC//BC B、AB//CD
C、BC//AD D、DC//A
二、填空题:(每小题3分,共9分)
1.在同一平面内,直线a,b相交于P,若a∥c,则b与c的
位置关系是______.
2.在同一平面内,若直线a,b,c满足a⊥b,a⊥c,则b与c的位置关系是______.
3.如图所示,BE是AB的延长线,量得∠CBE=∠A=∠C.
(1)由∠CBE=∠A可以判断______∥______,根据是_________.
(2)由∠CBE=∠C可以判断______∥______,根据是_________.
三、训练平台:(每小题15分,共30分)
如图所示,已知∠1=∠2,AB平分∠DAB,试说明DC∥AB.
如图所示,已知直线EF和AB,CD分别相交于K,H,且EG⊥AB,∠CHF=600,∠E= 30°,试说明AB∥CD.
四、提高训练:(共15分)
如图所示,已知直线a,b,c,d,e,且∠1=∠2,∠3+∠4=180°,则a与c平行吗 为 什么
五、探索发现:(共15分)
如图所示,请写出能够得到直线AB∥CD的所有直接条件.
六、中考题与竞赛题:(共8分)
(2000.江苏)如图所示,直线a,b被直线c所截,现给出下列四个条件:①∠1=∠ 5;②∠1=∠7;③∠2+∠3=180°;④∠4=∠7.其中能说明a∥b的条件序号为( )
A.①② B.①③ C.①④ D.③④
学后反思:
3
2
b
a
c
4
1
(1)∵∠2=∠3(已知)∠3=∠1(对顶角相等)
∴∠1=∠2 (等量代换)
∴a∥b(同位角相等,两条直线平行)
A
B
C
D
E
□ 自学导读·领悟知识我能行
【学习目标】1、了解平行线的概念,理解同一平面内两条直线间的位置关系;
2、掌握平行公理及平行线的画法。
【学习重点】平行线的概念、画法及平行公理。
【学习难点】解平行线的概念和根据几何语言画出图形。
【读书思考】1、什么是平行线?“平行”用什么表示?
2、平面内两条直线的位置关系有哪些?
3、平行公理及推论是什么?
【归纳小结】
知识点一、平行线定义
(1)用数学语言描述平行定义: 同一平面内,存在一条直线a与直线b不相交的位置,这时直线a与b互相平行.换言之,同一平面内, ________________叫做平行线.
(2)平行线表示法:
直线a与b是平行线,记作“∥”,这里“∥”是平行符号.
(3)在同一平面内,两条直线位置关系:
______或_______,两者必居其一.即两条直线___________________.
知识点二、平行公理及推论.
(1) 对照垂线的第一性质说出画图所得的结论.
(2) 在学生充分交流后,,归纳。
平行公理:_____________________________________________________.
(3) 比较平行公理和垂线的第一条性质.
共同点:都是“有且只有一条直线”,这表明与已知直线平行或垂直的直线存在并且是唯一的.
不同点:平行公理中所过的“一点”要在已知直线外,两垂线性质中对“一点”没有限制,可在直线上,也可在直线外.
(4) 归纳平行公理推论_____________________________________________________.
.【典题解析】
例1、判断下列说法是否正确?
(1)在同一平面内,两条线段不相交就平行;
(2)在同一平面内,平行于直线AB的直线只有一条。
(3)如果几条直线都和同一条直线平行,那么这几条直线都互相平行。
例2.读下列语句,并画出图形后判断.
(1)直线a、b互相垂直,点P是直线a、b外一点,过P点的直线c垂直于直线b.
(2)判断直线a、c的位置关系,并借助于三角尺、直尺验证.
例3.试说明三条直线的交点情况,进而判定在同一平面内三条直线的位置情况.
基础训练·基本题型我过关。
1、下列说法中错误的有( )个。
(1)两条不相交的直线叫做平行线
(2)经过直线外一点,能够画出一条直线与已知直线平行,并且只能画出一条
(3)如果a//b,b//c,则b//c (4)两条不平行的射线,在同一平面内一定相交
A、0 B、1 C、2 D、3
2、直线为空间内的两条直线,它们的位置关系是( )
A、平行 B、相交 C、异面 D、平行、相交或异面
3、在同一平面内的三条直线,如果要使其中两条且只有两条平行,那么它们( )
A、有三个交点 B、只有一个交点 C、有两个交点 D、没有交点
4、在同一平面内,直线相交于点O,且,则直线和的关系是( )
A、平行 B、相交 C、重合 D、以上都有可能
5、两条射线平行是指( )
A、两条射线都是水平的 B、两条射线都在同一直线上且方向相同
C、两条射线方向相反 D、两条射线所在直线平行
□ 能力提升·走进中考我能赢
1、在平面内有两两相交的3条直线,如果最多有个交点,最少有个交点,那么=( )
A、0 B、1 C、3 D、6
2、作图:在梯形ABCD中,上底、下底分别为AD、BC,点M为AB中点,
(1)过M点作MN//AD交CD于N A D
(2)MN和BC平行吗?为什么?
(3)用适当的方法度量并比较NC和ND的大小关系 M
B C
《5.2.1 平行线》补偿训练
(检测时间45分钟 满分100分)
班级_____________________ 姓名_______________得分_____
一、选择题:(每小题4分,共20分)
1.在同一平面内,两条不重合直线的位置关系可能是( )毛
A.平行或相交 B.垂直或相交; C.垂直或平行 D.平行、垂直或相交
2.下列说法正确的是( )
A.经过一点有一条直线与已知直线平行
B.经过一点有无数条直线与已知直线平行
C.经过一点有且只有一条直线与已知直线平行
D.经过直线外一点有且只有一条直线与已知直线平行
3.在同一平面内有三条直线,若其中有两条且只有两条直线平行,则它们交点的 个数为( )
A.0个 B.1个 C.2个 D.3个
4.下列说法正确的有( )
①不相交的两条直线是平行线;②在同一平面内,两条直线的位置关系有两种;
③若线段AB与CD没有交点,则AB∥CD;④若a∥b,b∥c,则a与c不相交.
A.1个 B.2个 C.3个 D.4个
5.过一点画已知直线的平行线,则( )
A.有且只有一条 B.有两条; C.不存在 D.不存在或只有一条
二、填空题:(每小题4分,共20分)
1.在同一平面内,____________________________________叫做平行线.
2.若AB∥CD,AB∥EF,则_____∥______,理由是__________________.
3.在同一平面内,若两条直线相交,则公共点的个数是________;若两条直线平 行,则公共点的个数是_________.
4.同一平面内的三条直线,其交点的个数可能为________.
5.直线L同侧有A,B,C三点,若过A,B的直线L1和过B,C的直线L2都与L平行,则A, B,C三点________,理论根据是___________________________.
三、解答题:(每小题12分,共48分)
已知直线a∥b,b∥c,c∥d,则a与d的关系是什么 为什么
2.如图所示,梯形ABCD中,AD∥BC,P是AB的中点,过P点作AD的平行线交DC于Q点.
(1)PQ与BC平行吗 为什么
(2)测量PQ与CQ的长,DQ与CQ是否相等
如图所示,a∥b,a与c相交,那么b与c相交吗 为什么
4.根据下列要求画图.
(1)如图(1)所示,过点A画MN∥BC;
(2)如图(2)所示,过点P画PE∥OA,交OB于点E,过点P画PH∥OB,交OA于点H;
(3)如图(3)所示,过点C画CE∥DA,与AB交于点E,过点C画CF∥DB,与AB的延长线交 于点F.
(1) (2) (3)
五、拓展提升:(共12分)
平面内有10条直线,无任何三条交于一点,欲使它们有31个交点,怎样才能办到
5.2.2 平行线的判定(第1课时)
□ 自学导读·领悟知识我能行
【学习目标】经历探索两直线平行条件的过程,理解两直线平行的条件.
【学习重点】探索两直线平行的条件。
【学习难点】理解“同位角相等,两条直线平行”。
【读书思考】
1如图(课本13面图5.2-5)在三角板移动的过程中,什么没有变?三角板经过点P的边与靠在直尺上的边所成的角没有变 。
2怎样判断两条直线平行?
【温故知新】
1. 判断:两条直线被第三条直线所截,如果同位角相等,那么内错角也相等.( )
2. 判断:两条直线被第三条直线所截,如果内错角互补,那么同旁内角相等.( )
3、在图1中,与∠1是同位角的是 ,与∠2是内错角的是 ,与∠A是同旁内角的是 。
4、如图2,∠5和∠7是 ,∠4和∠6是 ,∠1和∠5是 ,∠2与∠6是 ,∠1和∠3是 ,∠5和∠6是 。
5、如图3,∠ADC和∠BCD是直线 、 被直线 所截得到的 角;∠1和∠5是直线 、 被直线 所截得到的 角;∠4和∠9是直线 、 被直线 所截得到的 角;∠2和∠3是直线 、 被直线 所截得到的 角;
图1 图2 图3
【归纳小结】
知识点一、直线平行的条件
如图(课本13面图5.2-5)在三角板移动的过程中,什么没有变?三角板经过点P的边与靠在直尺上的边所成的角没有变 。
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单地说:同位角相等,两条直线平行.
符号语言: ∵∠1=∠2 ∴AB∥CD.
知识点二、
如图(课本14面5.2-7),你能说出木工用图中这种叫做角尺的工具画平行线的道理吗?
用角尺画平行线,实际上是画出了两个直角,根据“同位角相等,两条直线平行.”,可知这样画出的就是平行线。
如图,(1)如果∠2=∠3,能得出a∥b吗?(2)如果∠2+∠4=1800,能得出a∥b吗?
你能用文字语言概括上面的结论吗?
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简单地说:内错角相等,两直线平行.
符号语言:∵∠2=∠3 ∴a∥b.
(2)∵ ∠4+∠2=180°,∠4+∠1=180° (已知)
∴∠2=∠1 (同角的补角相等)
∴a∥b. (同位角相等,两条直线平行)
你能用文字语言概括上面的结论吗?
两条直线被第三条直线所截,如果同旁内角互补,那么两条直线平行.
简单地说:同旁内角互补,两直线平行
.符号语言: ∵∠4+∠2=180° ∴ a∥b.
【典题解析】
例1.右图,由图和已知条件,下列判断中正确的是( )
A.由∠1=∠6,得AB∥FG;
B.由∠1+∠2=∠6+∠7,得CE∥EI
C.由∠1+∠2+∠3+∠5=180°,得CE∥FI;
D.由∠5=∠4,得AB∥FG
2、已知直线a、b被直线c所截,且∠1+∠2=180°,试判断直线a、b的位置关系,并说明理由.
基础训练·基本题型我过关。
1.如图1,如果∠3=∠7,或______,那么______,理由是__________;如果∠5=∠3,或笔________,那么________, 理由是______________; 如果∠2+ ∠5= ______ 或者_______,那么a∥b,理由是__________.
(1) (2) (3)
2.如图2,若∠2=∠6,则______∥_______,如果∠3+∠4+∠5+∠6=180°, 那么____∥_______,如果∠9=_____,那么AD∥BC;如果∠9=_____,那么AB∥CD.
3.如图3所示,下列条件中,不能判定AB∥CD的是( )
A.AB∥EF,CD∥EF B.∠5=∠A; C.∠ABC+∠BCD=180° D.∠2=∠3
□ 能力提升·走进中考我能赢
1、如图,下列说法一定正确的是( )
A、∠1和∠4是同位角 B、∠2和∠3是内错角
C、∠3和∠4是同旁内角 D、∠5和∠6是同位角
2、在图7中,如果∠1与∠2、∠3与∠4、∠2与∠5分别互补,那么( )
A、 B、 C、 D、
图7
3、如图8,NO、QO分别是∠ONM和∠PQN的平分线,且∠QON=90°,那么MN与PQ( )
A、可能平行也可能相交 B、一定平行 C、一定相交 D、以上答案都不对
2.2 平行线的判定(第2课时)
□ 自学导读·领悟知识我能行
【学习目标】.经历分析题意,说理过程,能灵活地选用直线平行的规定方法进行说理。
【学习重点】直线平行的条件的应用
【学习难点】选取适当判定直线平行的方法进行说理是难点.
【读书思考】(课本17-18面)垂直总与直角联系在一起,我们学过哪些判断两条直线平行的方法?
【温故知新】
1.回忆怎样用移动三角尺的方法画两条平行线的, 其中直尺和三角尺的作用是什么
2.教师提出问题:学行线后,大家还能想出过一点画一条直线的平行线的新方法吗
3.下列说法错误的是 ( )
A.同位角不一定相等 B.内错角都相等 C.同旁内角可能相等 D.同旁内角互补,两直线平行
4.不相邻的两个直角,如果它们有一边在同一直线上,那么另一边相互 ( )
A.平行 B.垂直 C.平行或垂直 D.平行或垂直或相交
5.点A在直线外,直线AB⊥,直线AC⊥,那么直线AB、AC的关系是 。
【归纳小结】
知识点 判断两直线平行的方法
(1)平行线的定义:在同一平面内不相交的两条直线平行。
(2)平行公理的推论:如果两条直线都平行于第三条直线,那么这两条直线也互相平行。
(3)两直线平行的条件:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
【典题解析】
例1:在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行吗 为什么
请同学们写出多种证明方法:
例2 如图,点B在DC上,BE平分∠ABD,∠DBE=∠A,则BE∥AC,请说明理由。
分析:由BE平分∠ABD我们可以知道什么?联系∠DBE=∠A,我们又可以知道什么?由此能得出BE∥AC吗?为什么?
解:∵BE平分∠ABD
∴∠ABE=∠DBE(角平分线的定义)
又∠DBE=∠A
∴∠ABE=∠A(等量代换)
∴BE∥AC(内错角相等,两直线平行)
注意:用符号语言书写证明过程时,要步步有据。
基础训练·基本题型我过关。
1.如图,点E在CD上,点F在BA上,G是AD延长线上一点.
(1)若∠A=∠1,则可判断_______∥_______,因为________.
(2)若∠1=∠_________,则可判断AG∥BC,因为_________.
(3)若∠2+∠________=180°,则可判断CD∥AB,因为_______
___________________. (第1题)
2.如图,一个合格的变形管道ABCD需要AB边与CD边平行,若一个拐角∠ABC=72°,则另一个拐角∠BCD=_______时,这个管道符合要求.
( (第2题)
3.如图,下列判断不正确的是( )
A.因为∠1=∠4,所以DE∥AB
B.因为∠2=∠3,所以AB∥EC
C.因为∠5=∠A,所以AB∥DE
D.因为∠ADE+∠BED=180°,所以AD∥BE
4.如图,直线AB、CD被直线EF所截,使∠1=∠2≠90°,则( )
A.∠2=∠4 B.∠1=∠4
C.∠2=∠3 D.∠3=∠4
□ 能力提升·走进中考我能赢
1、在图10中有多少个角,找出这些角的内错角和同旁内角。
2.已知,如图2,点B在AC上,BD⊥BE,∠1+∠C=90°,问射线CF与BD平行吗 试用两种方法说明理由.
5.2.2 平行线的判定补偿训练
(检测时间45分钟 满分100分)
班级_____________________ 姓名_______________得分_____
一、选择题:(每小题3分,共18分)
1.如图1所示,下列条件中,能判断AB∥CD的是( )毛
A.∠BAD=∠BCD B.∠1=∠2; C.∠3=∠4 D.∠BAC=∠ACD
(1) (2) (3)
2.如图2所示,如果∠D=∠EFC,那么( )
A.AD∥BC B.EF∥BC C.AB∥DC D.AD∥EF
3.如图3所示,能判断AB∥CE的条件是( )
A.∠A=∠ACE B.∠A=∠ECD C.∠B=∠BCA D.∠B=∠ACE
4.下列说法错误的是( )
A.同位角不一定相等 B.内错角都相等 C.同旁内角可能相等 D.同旁内角互补,两直线平行
5.不相邻的两个直角,如果它们有一边在同一直线上,那么另一边相互( )
A.平行 B.垂直 C.平行或垂直 D.平行或垂直或相交
6.如图,DM是AD的延长线,若∠MDC=∠C,则( )
A、DC//BC B、AB//CD
C、BC//AD D、DC//A
二、填空题:(每小题3分,共9分)
1.在同一平面内,直线a,b相交于P,若a∥c,则b与c的
位置关系是______.
2.在同一平面内,若直线a,b,c满足a⊥b,a⊥c,则b与c的位置关系是______.
3.如图所示,BE是AB的延长线,量得∠CBE=∠A=∠C.
(1)由∠CBE=∠A可以判断______∥______,根据是_________.
(2)由∠CBE=∠C可以判断______∥______,根据是_________.
三、训练平台:(每小题15分,共30分)
如图所示,已知∠1=∠2,AB平分∠DAB,试说明DC∥AB.
如图所示,已知直线EF和AB,CD分别相交于K,H,且EG⊥AB,∠CHF=600,∠E= 30°,试说明AB∥CD.
四、提高训练:(共15分)
如图所示,已知直线a,b,c,d,e,且∠1=∠2,∠3+∠4=180°,则a与c平行吗 为 什么
五、探索发现:(共15分)
如图所示,请写出能够得到直线AB∥CD的所有直接条件.
六、中考题与竞赛题:(共8分)
(2000.江苏)如图所示,直线a,b被直线c所截,现给出下列四个条件:①∠1=∠ 5;②∠1=∠7;③∠2+∠3=180°;④∠4=∠7.其中能说明a∥b的条件序号为( )
A.①② B.①③ C.①④ D.③④
学后反思:
3
2
b
a
c
4
1
(1)∵∠2=∠3(已知)∠3=∠1(对顶角相等)
∴∠1=∠2 (等量代换)
∴a∥b(同位角相等,两条直线平行)
A
B
C
D
E
