1.1.2勾股定理的证明 课件(18张ppt)
文档属性
| 名称 | 1.1.2勾股定理的证明 课件(18张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-12 11:30:43 | ||
图片预览



文档简介
北师大版 八年级上
第一章 勾股定理
第2课时 勾股定理的证明及应用
1 探索勾股定理
学 习 目 标
1.掌握用面积法验证勾股定理,并能应用勾股定理解决一些实际问题.(重点)
2.经历勾股定理的验证过程,体会数形结合的思想和从特殊到一般的思想.(难点)
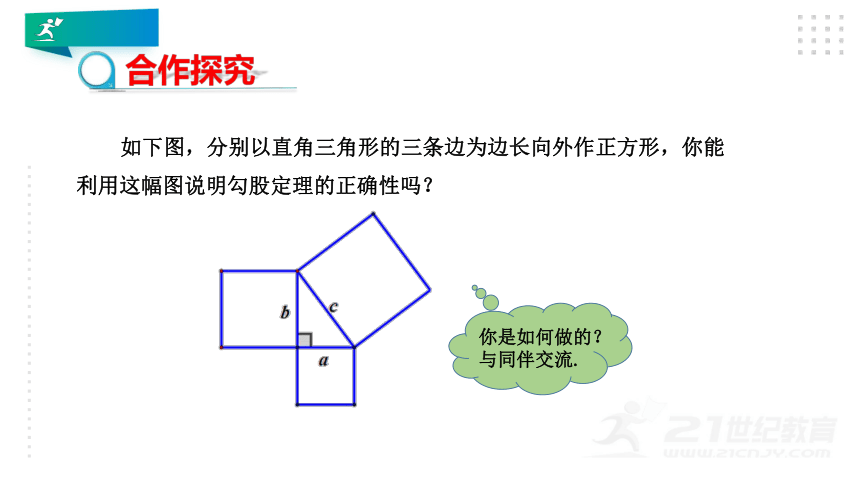
如下图,分别以直角三角形的三条边为边长向外作正方形,你能利用这幅图说明勾股定理的正确性吗?
你是如何做的?与同伴交流.
合作探究
割
补
A
B
C
D
活动1:小明的证明思路如下图,想一想:小明是怎样对大正方形进行割补的?
你能将所有三角形和正方形的面积用含a,b,c的关系式表示出来吗?
a+b
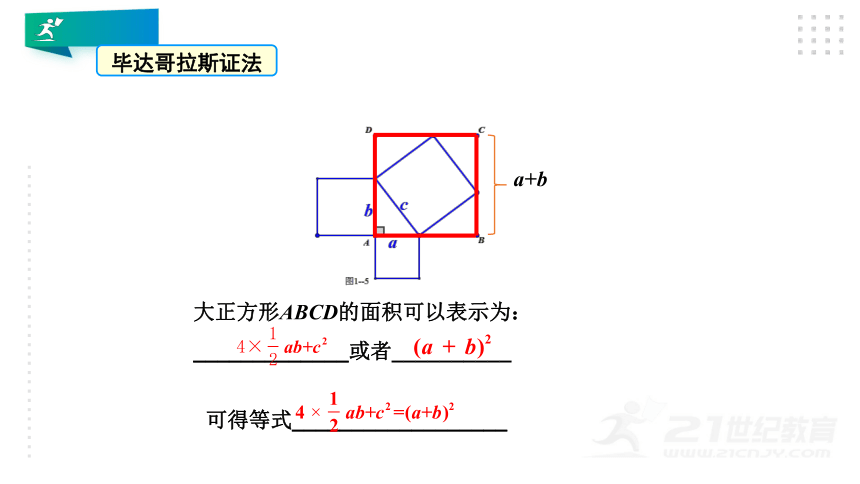
大正方形ABCD的面积可以表示为:
_____________或者__________
可得等式__________________
毕达哥拉斯证法
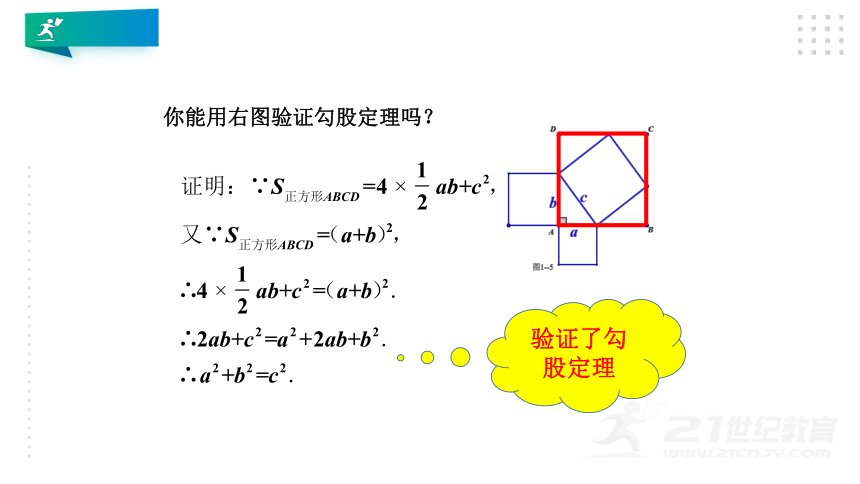
你能用右图验证勾股定理吗?
验证了勾股定理
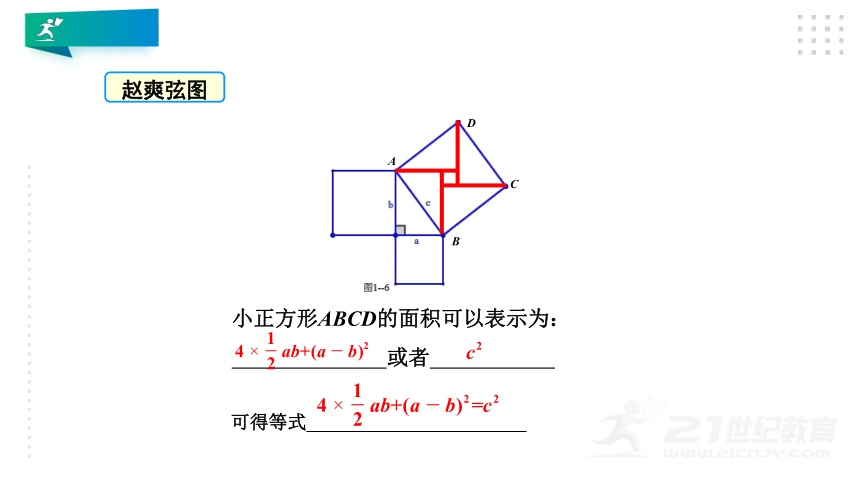
小正方形ABCD的面积可以表示为:
或者
A
B
C
D
可得等式
赵爽弦图
你能用右图验证勾股定理吗?
A
B
C
D
也验证了勾股定理
利用面积法进行证明
美国总统伽菲尔德利用下图证明了勾股定理,你能利用它验证勾股定理吗?说一说这个方法和本节的探索方法的联系.
美国总统证法
割补法是几何证明题中常用的方法,要注意这种方法的应用.你还能用其他方法证明勾股定理吗?
400 m
500 m
例. 我方侦察员小王在距离东西向公路400 m处侦察,发现一辆敌方汽车在公路上疾驶.他赶紧拿出红外测距仪,测得汽车与他相距400 m,10 s后,汽车与他相距500 m ,你能帮小王计算敌方汽车的速度吗?
例题讲解
如图是某沿江地区交通平面图,为了加快经济发展,该地区拟修建一条连接M,O,Q三城市的沿江高速公路,已知沿江高速公路的建设成本为5 000万元/km,该沿江高速公路的造价预计是多少?
30 km
40 km
50 km
120 km
随堂训练
课堂小结
勾股定理
内容
如果直角三角形两直角边分别为a,b,斜边为c,那么
毕达哥拉斯证法
赵爽弦图
美国总统证法
验证方法
1.如图,高速公路的同侧有A,B两个村庄,它们到高速公路所在直线MN的距离分别为AA1=2km,BB1=4km,A1B1=8km.现要在高速公路上A1、B1之间设一个出口P,使A,B两个村庄到P的距离之和最短,求这个最短距离和.
当堂检测
解:作点B关于MN的对称
点B′,连接AB′,交A1B1于
P点,连BP.
则AP+BP=AP+PB′=AB′,
易知P点即为到点A,B距离之和最短的点.
过点A作AE⊥BB′于点E,
则AE=A1B1=8km,B′E=AA1+BB1=2+4=6(km).
由勾股定理,得B′A2=AE2+B′E2=82+62,
∴AB′=10(km).即AP+BP=AB′=10km,
故出口P到A,B两村庄的最短距离和是10km.
2.如图,在一条公路上有A、B两站相距25km,C、D为两个小镇,已知DA⊥AB,CB ⊥AB, DA=15km,CB= 10km,现在要在公路边上建设一个加油站E,使得它到两镇的距离相等,请问E站应建在距A站多远处?
D
A
E
B
C
15
25-x
10
https://www.21cnjy.com/help/help_extract.php
第一章 勾股定理
第2课时 勾股定理的证明及应用
1 探索勾股定理
学 习 目 标
1.掌握用面积法验证勾股定理,并能应用勾股定理解决一些实际问题.(重点)
2.经历勾股定理的验证过程,体会数形结合的思想和从特殊到一般的思想.(难点)
如下图,分别以直角三角形的三条边为边长向外作正方形,你能利用这幅图说明勾股定理的正确性吗?
你是如何做的?与同伴交流.
合作探究
割
补
A
B
C
D
活动1:小明的证明思路如下图,想一想:小明是怎样对大正方形进行割补的?
你能将所有三角形和正方形的面积用含a,b,c的关系式表示出来吗?
a+b
大正方形ABCD的面积可以表示为:
_____________或者__________
可得等式__________________
毕达哥拉斯证法
你能用右图验证勾股定理吗?
验证了勾股定理
小正方形ABCD的面积可以表示为:
或者
A
B
C
D
可得等式
赵爽弦图
你能用右图验证勾股定理吗?
A
B
C
D
也验证了勾股定理
利用面积法进行证明
美国总统伽菲尔德利用下图证明了勾股定理,你能利用它验证勾股定理吗?说一说这个方法和本节的探索方法的联系.
美国总统证法
割补法是几何证明题中常用的方法,要注意这种方法的应用.你还能用其他方法证明勾股定理吗?
400 m
500 m
例. 我方侦察员小王在距离东西向公路400 m处侦察,发现一辆敌方汽车在公路上疾驶.他赶紧拿出红外测距仪,测得汽车与他相距400 m,10 s后,汽车与他相距500 m ,你能帮小王计算敌方汽车的速度吗?
例题讲解
如图是某沿江地区交通平面图,为了加快经济发展,该地区拟修建一条连接M,O,Q三城市的沿江高速公路,已知沿江高速公路的建设成本为5 000万元/km,该沿江高速公路的造价预计是多少?
30 km
40 km
50 km
120 km
随堂训练
课堂小结
勾股定理
内容
如果直角三角形两直角边分别为a,b,斜边为c,那么
毕达哥拉斯证法
赵爽弦图
美国总统证法
验证方法
1.如图,高速公路的同侧有A,B两个村庄,它们到高速公路所在直线MN的距离分别为AA1=2km,BB1=4km,A1B1=8km.现要在高速公路上A1、B1之间设一个出口P,使A,B两个村庄到P的距离之和最短,求这个最短距离和.
当堂检测
解:作点B关于MN的对称
点B′,连接AB′,交A1B1于
P点,连BP.
则AP+BP=AP+PB′=AB′,
易知P点即为到点A,B距离之和最短的点.
过点A作AE⊥BB′于点E,
则AE=A1B1=8km,B′E=AA1+BB1=2+4=6(km).
由勾股定理,得B′A2=AE2+B′E2=82+62,
∴AB′=10(km).即AP+BP=AB′=10km,
故出口P到A,B两村庄的最短距离和是10km.
2.如图,在一条公路上有A、B两站相距25km,C、D为两个小镇,已知DA⊥AB,CB ⊥AB, DA=15km,CB= 10km,现在要在公路边上建设一个加油站E,使得它到两镇的距离相等,请问E站应建在距A站多远处?
D
A
E
B
C
15
25-x
10
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
