1.1.1 勾股定理 课件(共19张PPT)
文档属性
| 名称 | 1.1.1 勾股定理 课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-12 11:30:43 | ||
图片预览


文档简介
北师大版 八年级上
第一章 勾股定理
第1课时 勾股定理
1 探索勾股定理
学 习 目 标
1.掌握勾股定理,了解利用拼图验证勾股定理的方法.(重点)
2.已知直角三角形两边的长,会利用勾股定理求第三边 .(重点)
3.能用勾股定理解决简单的问题 (难点)
如图,从电线杆离地面8m处向地面拉一条钢索,如果这条钢索在地面的固定点距离电线杆底部6m,那么需要多长的钢索?
新课导入
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图1-1
图1-2
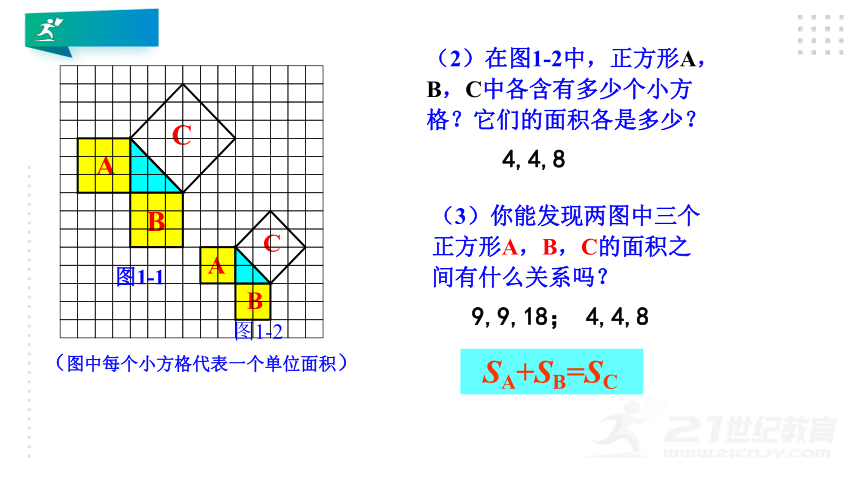
(1)观察图1—1.
正方形A中含有 个小方格,
即A的面积是 个单位面积;
正方形B中含有 个小方格,
即B的面积是 个单位面积;
正方形C中含有 个小方格,
即C的面积是 个单位面积;
你是怎样得到上面的结果的?与同学交流。
9
9
9
9
18
18
合作探究
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图1-1
图1-2
(2)在图1-2中,正方形A,B,C中各含有多少个小方格?它们的面积各是多少?
(3)你能发现两图中三个正方形A,B,C的面积之间有什么关系吗?
SA+SB=SC
4,4,8
9,9,18; 4,4,8
A
B
C
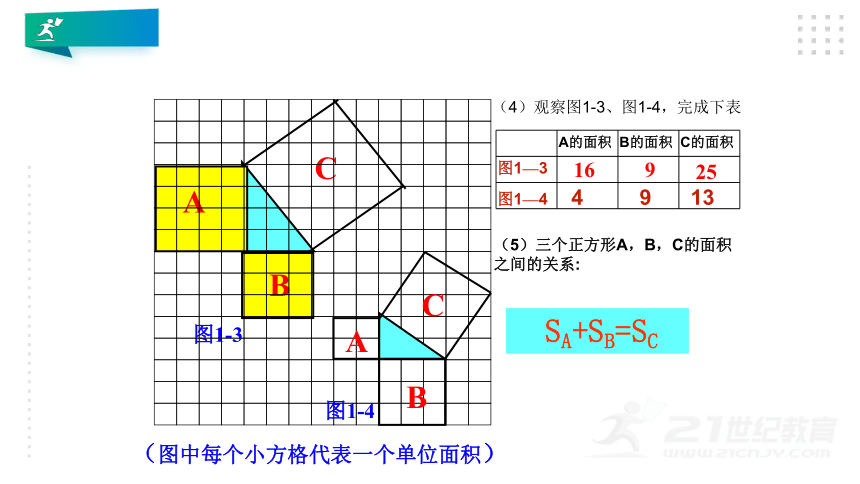
图1-3
(图中每个小方格代表一个单位面积)
9
16
25
SA+SB=SC
A
B
C
图1-4
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
图1—3
图1—4
A的面积
B的面积
C的面积
4
9
13
(4)观察图1-3、图1-4,完成下表
(5)三个正方形A,B,C的面积之间的关系:
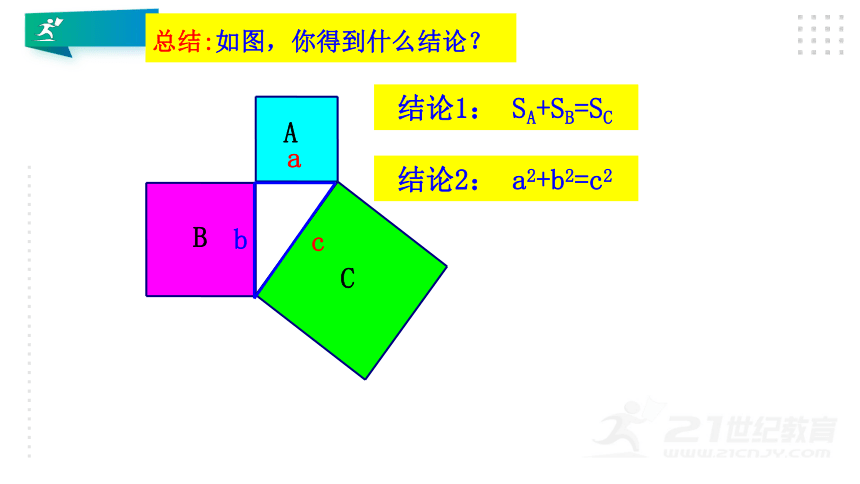
总结:如图,你得到什么结论?
A
B
C
a
c
b
结论1: SA+SB=SC
结论2: a2+b2=c2
勾股定理
如果直角三角形两直角边分别为a,b,斜边为c,那么
直角三角形两直角边的平方和等于斜边的平方
a
b
c
勾
(最短)
股
(较长)
弦(最长)
在西方又称毕达哥拉斯定理
知识讲解
例1 如果直角三角形两直角边长分别为 BC=5厘米 , AC=12厘米,求斜边AB的长度.
a
b
c
A
C
B
解:在Rt△ABC中根据勾股定理,得
答:斜边AB的长度为13厘米.
AC?+BC?=AB?,
,
,
.
.
.
例题讲解
∵
1.求下列直角三角形中未知边x的长度:
3
4
x
x
15
17
9
x
15
5
12
x
7
x
25
x
8
10
随堂训练
3
4
5
8
15
17
6
8
10
9
12
15
5
12
13
7
24
25
9
40
41
这些常见的直角三角形,要了解哦!
1.提示:
2.已知∠ACB=90°,CD⊥AB,AC=3,BC=4.
求CD的长.
A
D
B
C
3
4
课堂小结
勾股定理
内容
直角三角形两直角边的平方和等于斜边的平方
字母表示
如果直角三角形两直角边分别为a,b,斜边为c,那么
一、判断 1.△ABC的两边AB=5,AC=12,则BC=13 ( ) 2.△ABC的边a=6,b=8,则c=10 ( ) 二、填空 3.在△ABC中, ∠C=90°,AC=6,CB=8,则
△ABC面积为_____,斜边AB上的高为______.
?
?
24
4.8
A
B
C
D
当堂检测
4.在△ABC中,∠C=90?,
(1)??? 若a=5,b=12,则c=________;
(2)??? 若a=15,c=25,则b=________;
(3)??? 若c=61,b=60,则a=________;
(4)??? 若a:b=3:4,c=10,则a=________,b=________;
(5)??? 若a:c=3:5 ,b=8,则a=________.
20
13
11
6
8
6
5. 一高为2.5米的木梯,架在高为2.4米的墙上(如图),这时梯脚与墙的距离是多少?
A
B
C
解:在Rt△ABC中,根据勾股定理,得 BC2+AC2=AB2, 即 BC2+2.42 = 2.52,
∴ BC=0.7(米).
6.小明的妈妈买了一部29英寸(74厘米)的电视机.小明量了电视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉得一定是售货员搞错了.你能解释这是为什么吗?
我们通常所说的29英寸或74厘米的电视机,是指其荧屏对角线的长度,而不是其长或宽
所以售货员没搞错.
又因为荧屏对角线大约为74厘米,
因为
https://www.21cnjy.com/help/help_extract.php
第一章 勾股定理
第1课时 勾股定理
1 探索勾股定理
学 习 目 标
1.掌握勾股定理,了解利用拼图验证勾股定理的方法.(重点)
2.已知直角三角形两边的长,会利用勾股定理求第三边 .(重点)
3.能用勾股定理解决简单的问题 (难点)
如图,从电线杆离地面8m处向地面拉一条钢索,如果这条钢索在地面的固定点距离电线杆底部6m,那么需要多长的钢索?
新课导入
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图1-1
图1-2
(1)观察图1—1.
正方形A中含有 个小方格,
即A的面积是 个单位面积;
正方形B中含有 个小方格,
即B的面积是 个单位面积;
正方形C中含有 个小方格,
即C的面积是 个单位面积;
你是怎样得到上面的结果的?与同学交流。
9
9
9
9
18
18
合作探究
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图1-1
图1-2
(2)在图1-2中,正方形A,B,C中各含有多少个小方格?它们的面积各是多少?
(3)你能发现两图中三个正方形A,B,C的面积之间有什么关系吗?
SA+SB=SC
4,4,8
9,9,18; 4,4,8
A
B
C
图1-3
(图中每个小方格代表一个单位面积)
9
16
25
SA+SB=SC
A
B
C
图1-4
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
图1—3
图1—4
A的面积
B的面积
C的面积
4
9
13
(4)观察图1-3、图1-4,完成下表
(5)三个正方形A,B,C的面积之间的关系:
总结:如图,你得到什么结论?
A
B
C
a
c
b
结论1: SA+SB=SC
结论2: a2+b2=c2
勾股定理
如果直角三角形两直角边分别为a,b,斜边为c,那么
直角三角形两直角边的平方和等于斜边的平方
a
b
c
勾
(最短)
股
(较长)
弦(最长)
在西方又称毕达哥拉斯定理
知识讲解
例1 如果直角三角形两直角边长分别为 BC=5厘米 , AC=12厘米,求斜边AB的长度.
a
b
c
A
C
B
解:在Rt△ABC中根据勾股定理,得
答:斜边AB的长度为13厘米.
AC?+BC?=AB?,
,
,
.
.
.
例题讲解
∵
1.求下列直角三角形中未知边x的长度:
3
4
x
x
15
17
9
x
15
5
12
x
7
x
25
x
8
10
随堂训练
3
4
5
8
15
17
6
8
10
9
12
15
5
12
13
7
24
25
9
40
41
这些常见的直角三角形,要了解哦!
1.提示:
2.已知∠ACB=90°,CD⊥AB,AC=3,BC=4.
求CD的长.
A
D
B
C
3
4
课堂小结
勾股定理
内容
直角三角形两直角边的平方和等于斜边的平方
字母表示
如果直角三角形两直角边分别为a,b,斜边为c,那么
一、判断 1.△ABC的两边AB=5,AC=12,则BC=13 ( ) 2.△ABC的边a=6,b=8,则c=10 ( ) 二、填空 3.在△ABC中, ∠C=90°,AC=6,CB=8,则
△ABC面积为_____,斜边AB上的高为______.
?
?
24
4.8
A
B
C
D
当堂检测
4.在△ABC中,∠C=90?,
(1)??? 若a=5,b=12,则c=________;
(2)??? 若a=15,c=25,则b=________;
(3)??? 若c=61,b=60,则a=________;
(4)??? 若a:b=3:4,c=10,则a=________,b=________;
(5)??? 若a:c=3:5 ,b=8,则a=________.
20
13
11
6
8
6
5. 一高为2.5米的木梯,架在高为2.4米的墙上(如图),这时梯脚与墙的距离是多少?
A
B
C
解:在Rt△ABC中,根据勾股定理,得 BC2+AC2=AB2, 即 BC2+2.42 = 2.52,
∴ BC=0.7(米).
6.小明的妈妈买了一部29英寸(74厘米)的电视机.小明量了电视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉得一定是售货员搞错了.你能解释这是为什么吗?
我们通常所说的29英寸或74厘米的电视机,是指其荧屏对角线的长度,而不是其长或宽
所以售货员没搞错.
又因为荧屏对角线大约为74厘米,
因为
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
