2.1.2 感受无理数 课件(共23张PPT)
文档属性
| 名称 | 2.1.2 感受无理数 课件(共23张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-12 11:30:43 | ||
图片预览







文档简介
北师大版 八年级上
第二章 实数
第二课时
2.1 认识无理数
感受无理数
学 习 目 标
1.理解无理数的定义,并会判断一个数是否为无理数。分清有理数与无理数的区别.(重点)
2.借助计算器,利用无限逼近的思想,探索无理数是无限不循环小数,会求一个无理数的近似值.(难点)
1.有理数是如何分类的?
有理数
2.除上面的数以外,我们还学习过哪些不同的数?如圆周率π,0.020020002…,如a2=2,b2=5中的a,b不是整数,能不能转化成分数呢?
整数:如-1,0,1,2,3,……
分数:如 ……
知识回顾
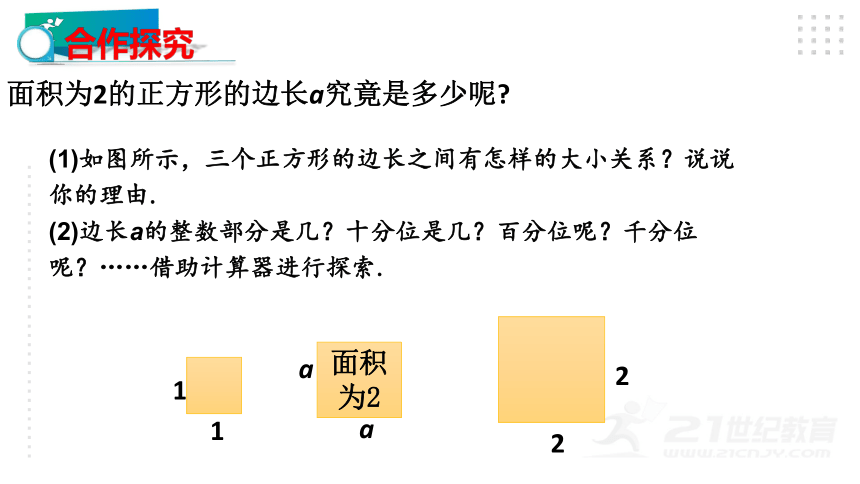
面积为2的正方形的边长a究竟是多少呢?
(1)如图所示,三个正方形的边长之间有怎样的大小关系?说说你的理由.
(2)边长a的整数部分是几?十分位是几?百分位呢?千分位呢?……借助计算器进行探索.
1
1
面积为2
a
a
2
2
合作探究
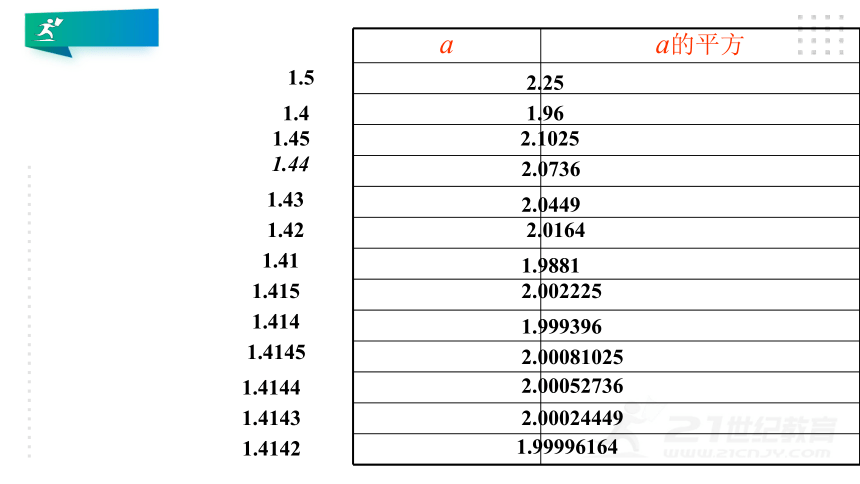
a
a的平方
2.25
1.96
2.1025
2.0449
2.0736
2.0164
1.9881
2.002225
1.999396
2.00052736
2.00024449
1.99996164
2.00081025
1.4
1.5
1.45
1.44
1.43
1.42
1.41
1.415
1.414
1.4145
1.4144
1.4143
1.4142
(3)小明将他的探索过程整理如下,你的结果呢?
边长a
面积S
111.41.961.411.98811.4141.9993961.41421.99996164 a是介于1和2之间的一个数,既不是整数,也不是分数,则a一定不是有理数.
如果写成小数形式,它是有限小数吗?
事实上,a=1.41421356…,它是一个无限不循环小数.
探索a是多少?
a =1.41421356…
(1)请大家用上面的方法估计面积为5的正方形的边长b的值(结果精确到0.1),并用计算器验证你的估计.
(2)如果结果精确到0.01呢? (提示:精确到0.1,b≈2.2,精确到0.01,b≈2.24)
做一做
用上面的方法估计面积为5的正方形的边长b的值.边长b会不会算到某一位时,它的平方恰好等于5?
如果b算到某一位时,它的平方恰好等于5,即b是一个有限小数,那么它的平方一定是一个有限小数,而不可能是5,所以b不可能是有限小数.事实上,b=2.236 067 978…它是一个无限不循环小数.
同样,对于体积为2的正方体,借用计算器,可以得到它的棱长c=1.259 921 05…,它也是一个无限不循环小数.
做一做
把下列各数表示成小数,你发现了什么?
3,
解:3=3.0
分数化成小数,最终此小数的形式有哪几种情况?
分数只能化成有限小数或无限循环小数,即任何有限小数或无限循环小数都是有理数.
议一议
下列各数中,哪些是有理数?哪些是无理数?
3.14, - , ,0.1010001000001…(相邻两个1之间0的个数逐次加2).
解:有理数有:3.14, - , ;
无理数有:0.1010001000001…(相邻两 个1之间0的个数逐次加2).
例题讲解
2.任何一个有理数都可以化成分数 的形式(q≠0,p,q为整数且互质),而无理数不能.
1.无理数是无限不循环小数,有理数是有限小数或无限循环小数.
温馨提示
确定x2=a(a≥0)中正数x的近似值的方法:
1.确定正数x的整数部分.根据平方的定义,把x夹在两个连续的正整数之间,确定其整数部分。
例如:求x2=5中的正数x的整数部分,因为22<5<32,即22知识拓展
(1)将这两个整数平方和的平均数与a比较,预测十分位上数字的取值范围,如两个整数2和3的平方和的平均数为 = 6.5>5,所以x的十分位上的数字一定比3小,不妨设x≈2.2.
2.确定x的小数部分十分位上的数字.
(2)设误差为k(k必为一个纯小数,且k可能为负数),则x=2.2+k,所以(2.2+k)2=5,所以4.84+4.4k+k2=5,因为k是小数,所以k2很小,把它舍去,所以4.84+4.4k=5,所以k≈0.036,所以x=2.2+k≈2.2+0.036=2.236.
实际估算中,整数部分的数字容易估计,十分位上的数字也可以采用试验的方法进行估计,即2.12=4.41,2.22=4.84,2.32=5.29,因为4.84<5<5.29,所以2.221、下列各数中,哪些是有理数?哪些是无理数?
0.351,- ,3.14159,-5.2323332…,
123456789101112…(由相继的正整数组成).
解:有理数有0.351,- , ,3.14159
无理数有-5.2323332…,123456789101112….
当堂检测
(1)有限小数是有理数; ( )
(2)无限小数都是无理数; ( )
(3)无理数都是无限小数; ( )
(4)有理数是有限小数. ( )
2 判断题
╳
√
√
╳
3.下列说法中正确的是 ( )
A.无限小数都是无理数
B.有限小数是无理数
C.无理数都是无限小数
D.有理数是有限小数
C
4 .以下各正方形的边长是无理数的是 ( )
A.面积为25的正方形
B.面积为 的正方形
C.面积为8的正方形
D.面积为1.44的正方形
C
5.一个直角三角形两条直角边的长分别是3和5,则斜边长a是有理数吗?
5
3
a
解:由勾股定理得:a2=32+52,即a2=34。因为不存在有理数的平方等于34,所以a不是有理数.
有理数:有限小数或无限循环小数
无理数:无限不循环小数
数
整数
分数
课堂小结
https://www.21cnjy.com/help/help_extract.php
第二章 实数
第二课时
2.1 认识无理数
感受无理数
学 习 目 标
1.理解无理数的定义,并会判断一个数是否为无理数。分清有理数与无理数的区别.(重点)
2.借助计算器,利用无限逼近的思想,探索无理数是无限不循环小数,会求一个无理数的近似值.(难点)
1.有理数是如何分类的?
有理数
2.除上面的数以外,我们还学习过哪些不同的数?如圆周率π,0.020020002…,如a2=2,b2=5中的a,b不是整数,能不能转化成分数呢?
整数:如-1,0,1,2,3,……
分数:如 ……
知识回顾
面积为2的正方形的边长a究竟是多少呢?
(1)如图所示,三个正方形的边长之间有怎样的大小关系?说说你的理由.
(2)边长a的整数部分是几?十分位是几?百分位呢?千分位呢?……借助计算器进行探索.
1
1
面积为2
a
a
2
2
合作探究
a
a的平方
2.25
1.96
2.1025
2.0449
2.0736
2.0164
1.9881
2.002225
1.999396
2.00052736
2.00024449
1.99996164
2.00081025
1.4
1.5
1.45
1.44
1.43
1.42
1.41
1.415
1.414
1.4145
1.4144
1.4143
1.4142
(3)小明将他的探索过程整理如下,你的结果呢?
边长a
面积S
1
如果写成小数形式,它是有限小数吗?
事实上,a=1.41421356…,它是一个无限不循环小数.
探索a是多少?
a =1.41421356…
(1)请大家用上面的方法估计面积为5的正方形的边长b的值(结果精确到0.1),并用计算器验证你的估计.
(2)如果结果精确到0.01呢? (提示:精确到0.1,b≈2.2,精确到0.01,b≈2.24)
做一做
用上面的方法估计面积为5的正方形的边长b的值.边长b会不会算到某一位时,它的平方恰好等于5?
如果b算到某一位时,它的平方恰好等于5,即b是一个有限小数,那么它的平方一定是一个有限小数,而不可能是5,所以b不可能是有限小数.事实上,b=2.236 067 978…它是一个无限不循环小数.
同样,对于体积为2的正方体,借用计算器,可以得到它的棱长c=1.259 921 05…,它也是一个无限不循环小数.
做一做
把下列各数表示成小数,你发现了什么?
3,
解:3=3.0
分数化成小数,最终此小数的形式有哪几种情况?
分数只能化成有限小数或无限循环小数,即任何有限小数或无限循环小数都是有理数.
议一议
下列各数中,哪些是有理数?哪些是无理数?
3.14, - , ,0.1010001000001…(相邻两个1之间0的个数逐次加2).
解:有理数有:3.14, - , ;
无理数有:0.1010001000001…(相邻两 个1之间0的个数逐次加2).
例题讲解
2.任何一个有理数都可以化成分数 的形式(q≠0,p,q为整数且互质),而无理数不能.
1.无理数是无限不循环小数,有理数是有限小数或无限循环小数.
温馨提示
确定x2=a(a≥0)中正数x的近似值的方法:
1.确定正数x的整数部分.根据平方的定义,把x夹在两个连续的正整数之间,确定其整数部分。
例如:求x2=5中的正数x的整数部分,因为22<5<32,即22
(1)将这两个整数平方和的平均数与a比较,预测十分位上数字的取值范围,如两个整数2和3的平方和的平均数为 = 6.5>5,所以x的十分位上的数字一定比3小,不妨设x≈2.2.
2.确定x的小数部分十分位上的数字.
(2)设误差为k(k必为一个纯小数,且k可能为负数),则x=2.2+k,所以(2.2+k)2=5,所以4.84+4.4k+k2=5,因为k是小数,所以k2很小,把它舍去,所以4.84+4.4k=5,所以k≈0.036,所以x=2.2+k≈2.2+0.036=2.236.
实际估算中,整数部分的数字容易估计,十分位上的数字也可以采用试验的方法进行估计,即2.12=4.41,2.22=4.84,2.32=5.29,因为4.84<5<5.29,所以2.22
0.351,- ,3.14159,-5.2323332…,
123456789101112…(由相继的正整数组成).
解:有理数有0.351,- , ,3.14159
无理数有-5.2323332…,123456789101112….
当堂检测
(1)有限小数是有理数; ( )
(2)无限小数都是无理数; ( )
(3)无理数都是无限小数; ( )
(4)有理数是有限小数. ( )
2 判断题
╳
√
√
╳
3.下列说法中正确的是 ( )
A.无限小数都是无理数
B.有限小数是无理数
C.无理数都是无限小数
D.有理数是有限小数
C
4 .以下各正方形的边长是无理数的是 ( )
A.面积为25的正方形
B.面积为 的正方形
C.面积为8的正方形
D.面积为1.44的正方形
C
5.一个直角三角形两条直角边的长分别是3和5,则斜边长a是有理数吗?
5
3
a
解:由勾股定理得:a2=32+52,即a2=34。因为不存在有理数的平方等于34,所以a不是有理数.
有理数:有限小数或无限循环小数
无理数:无限不循环小数
数
整数
分数
课堂小结
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
