2.6 实数 课件（共19张PPT）

北师大版 八年级上
第二章 实数
2.6 实数　
学 习 目 标
1.了解实数的意义，能对实数按要求分类；（重点）
2.了解有理数的运算法则在实数范围内仍然适用；（重点）
3.能利用性质或公式对实数进行简单的化简.（难点）
把下列各数分别填入相应的括号内：
，
，
，
，
，
，
，
，
，
，
，
.
有理数
无理数
知识回顾
有理数
整数
分数
有限小数
无限循环小数
无理数
无限不循环小数
有理数和无理数统称为 。
实数
即 实数可以分为有理数和无理数。
有理数的分类：
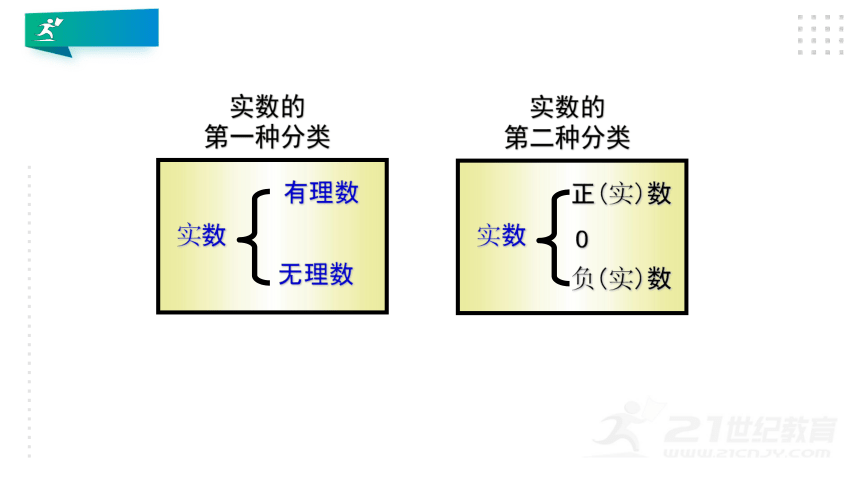
实数
有理数
无理数
实数
实数的分类
知识讲解
1、实数的分类
无理数和有理数一样，也 有正负之分。
如：
注意
有了实数概念后，
以前的“正数”与“负数”的概念也随之得到了扩充——
【 正数】
大于 0 的实数。
包括所有的正有理数和正无理数.
【 负数】
小于 0 的实数。
包括所有的负有理数和负无理数.
正数和负数组成能构成实数吗？
答：
不能。
“ 0 也是实数 ”.
实数
实数的
第一种分类
有理数
无理数
实数
实数的
第二种分类
正（实）数
负（实）数
0
把下列各数分别填入相应的括号内：
正数集合
负数集合
即学即练
…
…
和有理数范围内 的相反数、倒数、绝对值的意义 ，完全一样。
例如：
2、实数范围内的相关概念
想一想
（1） a 是一个实数 ，它的相反数为 ？
（2） 如果 a ≠ 0 ，那么它的倒数为 。
-a
1.（1） 的倒数是 ，相反数是_____。
（2）绝对值为 的数是_______，绝对值小于
的整数是_________。
（3）若 ，且xy>0，则 x+y= 。
即学即练
2. 实数 a,b 的位置如图
化简 |a + b| – |a – b|.
a
0
b
解:由数轴可知，a+b<0，a－b<0，从而
原式=－(a＋b)－[－（a－b）]
= －a－b＋（a－b）
= －a－b＋（a－b）
= －a－b＋a－b
= －2b.
（1） 如图 2—5，
-2
-1
0
1
2
图 2—5
OA=OB
1
B
A
数轴上的 点A对应的数是什么？
OB =
点A 对应的数是
（2） 如果将所有有理数都标到数轴上 ，那么数轴被填满了吗？
答：
填不满。
数轴上还有无数多个无理数对应的点。
3、实数与数轴
每一个实数都可以用数轴上的一个点来表示。
-2
-1
0
1
2
反过来 ，数轴上的每一个点都表示一个实数。
（数?点）
（点?数）
A
{ 实数 }：
数 a
数 a
点 A
一一对应
3、在数轴上作出 对应的点。
-2
-1
0
1
2
1.化简：
2.大于 而小于 的所有整数为________。
-3,-2,-1,0,1,2
3. 的绝对值是 ；
相反数是 __________ 。
4.在实数
A.-2 B.0 C. D.
A
当堂检测
6.已知a,b,c在数轴上的对应点如图所示。化简:
o
b
a
c
-1
实数
有理数和无理数统称实数
在实数范围内，相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样.
实数与数轴上的点一一对应
课堂小结
https://www.21cnjy.com/help/help_extract.php