《2.1圆》同步培优提升专题训练(附答案)2021-2022学年九年级数学苏科版上册
文档属性
| 名称 | 《2.1圆》同步培优提升专题训练(附答案)2021-2022学年九年级数学苏科版上册 |  | |
| 格式 | doc | ||
| 文件大小 | 141.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-16 11:05:38 | ||
图片预览



文档简介
2021-2022学年苏科版九年级数学上册《2.1圆》同步培优提升专题训练(附答案)
一.选择题(共8小题)
1.⊙O的半径为4cm,点P到圆心O的距离为5cm,点P与⊙O的位置关系是( )
A.点P在⊙O内 B.点P在⊙O上 C.点P在⊙O外 D.无法确定
2.在平面直角坐标系xOy中,⊙O的半径为2,点A(1,)与⊙O的位置关系是( )
A.在⊙O上 B.在⊙O内 C.在⊙O外 D.不能确定
3.已知⊙O与点P在同一平面内,如果⊙O的直径为6,线段OP的长为4,则下列说法正确的是( )
A.点P在⊙O上
B.点P在⊙O内
C.点P在⊙O外
D.无法判断点P与⊙O的位置关系
4.已知AB是半径为6的圆的一条弦,则AB的长不可能是( )
A.8 B.10 C.12 D.14
5.数轴上有两个点A和B,点B表示实数6,点A表示实数a,⊙B半径为4.若点A在⊙B内,则( )
A.a<2或a>10 B.2<a<10 C.a>2 D.a<10
6.如图,在矩形ABCD中,AB=6,AD=8,若以点A为圆心,8为半径作⊙A,则下列各点在⊙A外的是( )
A.点A B.点B C.点C D.点D
7.直角坐标系的原点为O,⊙O半径为5,点P(4,﹣3)( )
A.在⊙O内 B.在⊙O上 C.在⊙O外 D.无法确定
8.已知⊙O的半径为1,AO=d,且关于x的方程x2﹣2dx+1=0有两个相等的实数根,则点A与⊙O的位置关系是( )
A.在⊙O内 B.在⊙O外 C.在⊙O上 D.无法确定
二.填空题(共8小题)
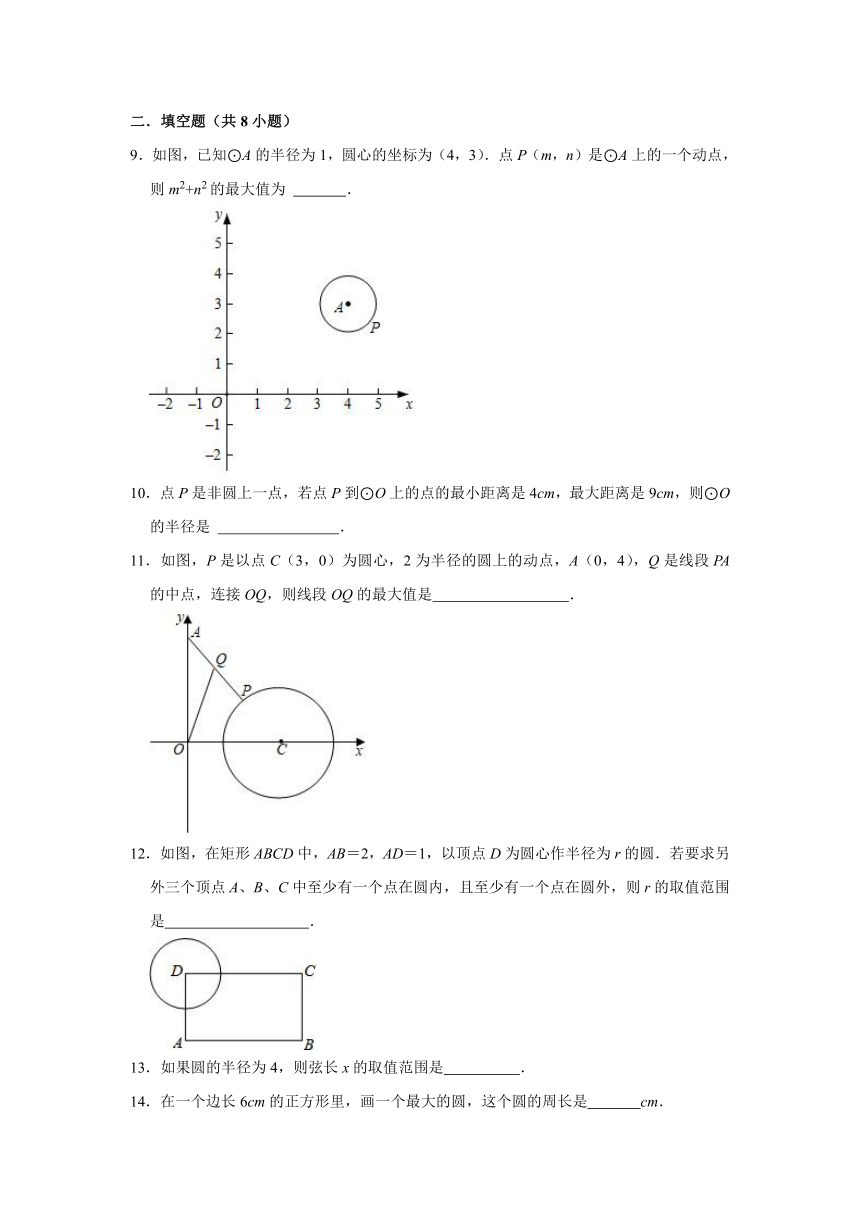
9.如图,已知⊙A的半径为1,圆心的坐标为(4,3).点P(m,n)是⊙A上的一个动点,则m2+n2的最大值为 .
10.点P是非圆上一点,若点P到⊙O上的点的最小距离是4cm,最大距离是9cm,则⊙O的半径是 .
11.如图,P是以点C(3,0)为圆心,2为半径的圆上的动点,A(0,4),Q是线段PA的中点,连接OQ,则线段OQ的最大值是 .
12.如图,在矩形ABCD中,AB=2,AD=1,以顶点D为圆心作半径为r的圆.若要求另外三个顶点A、B、C中至少有一个点在圆内,且至少有一个点在圆外,则r的取值范围是 .
13.如果圆的半径为4,则弦长x的取值范围是 .
14.在一个边长6cm的正方形里,画一个最大的圆,这个圆的周长是 cm.
15.已知甲圆的直径等于乙圆的半径,且甲乙两圆的面积之和为50cm2,那么甲圆的面积是 cm2.
16.已知⊙O的半径为1,点P到圆心的距离为m,且关于x的一元二次方程x2﹣2x+m=0有两个不相等实数根,则点P与⊙O位置关系是 .
三.解答题(共4小题)
17.如图,△ABC中,∠ACB=90°,BC=5cm,AC=10cm,CD为中线,以C为圆心,以cm长为半径作圆,则点A,B,D与⊙C的位置关系如何?
18.如图,AB、CD为⊙O中两条直径,点E、F在直径CD上,且CE=DF.
求证:AF=BE.
19.如图,BD=OD,∠B=38°,求∠AOD的度数.
20.在矩形ABCD中,AB=3cm,BC=3cm,以点A为圆心AB为半径作圆,则B,C,D三点分别与⊙A有怎样的位置关系?AC的中点M与⊙A又有怎样的位置关系?
参考答案
一.选择题(共8小题)
1.解:∵OP=5>4,
∴点P与⊙O的位置关系是点在圆外.
故选:C.
2.解:∵点A(1,),
∴AO==2,
∵⊙O的半径为2,
∴点A在⊙O上,
故选:A.
3.解:∵⊙O的半径是3,线段OP的长为4,
即点P到圆心的距离大于圆的半径,
∴点P在⊙O外.
故选:C.
4.解:∵圆的半径为6,
∴直径为12,
∵AB是一条弦,
∴AB的长应该小于等于12,不可能为的14,
故选:D.
5.解:∵点B表示实数6,⊙B半径为4.
∴数轴与⊙B的交点表示的数为2或10,
∵点A表示实数a,点A在⊙B内,
∴2<a<10,
故选:B.
6.解:连接AC,
在矩形ABCD中,AB=6,AD=8,
∴BC=AD=8,∠B=90°,
∴AC==10,
∵AB=6<8,AC=10>8,AD=8,
∴点D在⊙A上,点C在⊙A外,点B在⊙A内.
故选:C.
7.解:∵圆心P的坐标为(4,﹣3),
∴OP==5.
∵⊙O的半径为5,
∴点P在⊙O上.
故选:B.
8.解:∵a=1,b=﹣2d,c=1,
∴△=b2﹣4ac=(﹣2d)2﹣4×1×1=4d2﹣4=0,
解得:d=1.
则点A在⊙O上.
故选:C.
二.填空题(共8小题)
9.解:作射线OA交⊙O于P′点,如图,
∵圆心A的坐标为(4,3),点P的坐标为(m,n),
∴OA==5,OP=,
∴m2+n2是点P点圆点的距离的平方,
∴当点P运动到P′处,点P离圆点最远,即m2+n2有最大值,
此时OP=OA+AP′=5+1=6,则m2+n2=36.
故答案为:36.
10.解:分为两种情况:
①当点在圆内时,如图1,
∵点到圆上的最小距离PB=4cm,最大距离PA=9cm,
∴直径AB=4cm+9cm=13cm,
∴半径r=6.5cm;
②当点在圆外时,如图2,
∵点到圆上的最小距离PB=4cm,最大距离PA=9cm,
∴直径AB=9cm﹣4cm=5cm,
∴半径r=2.5cm;
故答案为:6.5cm或2.5cm.
11.解:作点A(0,4)关于x轴的对称点B(0,﹣4),连接BP,
∵Q是线段PA的中点,
∴OQ为△ABP的中位线,
∴OQ=BP,
当BP最大时,OQ最大,
而BP过圆心C时,PB最大,如图,点P运动到P′位置时,BP最大,
∵点C(3,0),
∴OC=3,
∵OB=4,
∴BC==5,
∴BP′=5+2=7,
∴线段OQ的最大值是.
故答案为.
12.解:在直角△ABD中,CD=AB=2,AD=1,
则BD==.
由图可知1<r<.
故答案为:1<r<.
13.解:∵直径为圆中最长的弦,
∴0<x≤8.
故答案为0<x≤8.
14.解:根据题意,最大的圆为正方形的内切圆,
所以最大圆的直径为正方形的边长,
所以这个圆的周长为2π×()=6π(cm).
故答案为6π.
15.解:设乙圆的半径为rcm,则甲圆的半径为 cm,
由圆的面积公式可得:,
解得:πr2=40,
所以甲圆的面积=50﹣40=10(cm2),
故答案为:10.
16.解:∵a=1,b=﹣2,c=m,
∴△=b2﹣4ac=(﹣2)2﹣4×1×m=4﹣4m>0,
解得:m<1.
则点P在⊙O内部.
故答案为:点P在圆内.
三.解答题(共4小题)
17.解:在△ABC中,∠ACB=90°,BC=5cm,AC=10cm,
∴AB==5(cm),
∵CD为中线,
∴CD=AB=cm,
∵AC=10cm>cm,
∴点A在⊙C的外面,
∵BC=5cm<cm,
∴点B在⊙C的内部,
∵CD=cm,
∴点D在⊙C上.
18.解:∵AB、CD为⊙O中两条直径,
∴OA=OB,OC=OD,
∵CE=DF,
∴OE=OF,
在△AOF和△BOE中,
,
∴△AOF≌△BOE(SAS),
∴AF=BE.
19.解:∵BD=OD,∠B=38°,
∴∠DOB=∠B=38°,
∴∠ADO=∠DOB+∠B=2×38°=76°,
∵OA=OD,
∴∠A=∠ADO=76°,
∴∠AOD=180°﹣∠A﹣∠ADO=180°﹣76°﹣76°=28°.
20.解:如图,
观察图象可知,点B在⊙A上,点C,点D在⊙A外.
∵四边形ABCD是矩形,
∴∠ABC=90°,
∵AB=3,BC=3,
∴AC===6,
∴AM=AC=3=AB,
∴点M在⊙A上.
一.选择题(共8小题)
1.⊙O的半径为4cm,点P到圆心O的距离为5cm,点P与⊙O的位置关系是( )
A.点P在⊙O内 B.点P在⊙O上 C.点P在⊙O外 D.无法确定
2.在平面直角坐标系xOy中,⊙O的半径为2,点A(1,)与⊙O的位置关系是( )
A.在⊙O上 B.在⊙O内 C.在⊙O外 D.不能确定
3.已知⊙O与点P在同一平面内,如果⊙O的直径为6,线段OP的长为4,则下列说法正确的是( )
A.点P在⊙O上
B.点P在⊙O内
C.点P在⊙O外
D.无法判断点P与⊙O的位置关系
4.已知AB是半径为6的圆的一条弦,则AB的长不可能是( )
A.8 B.10 C.12 D.14
5.数轴上有两个点A和B,点B表示实数6,点A表示实数a,⊙B半径为4.若点A在⊙B内,则( )
A.a<2或a>10 B.2<a<10 C.a>2 D.a<10
6.如图,在矩形ABCD中,AB=6,AD=8,若以点A为圆心,8为半径作⊙A,则下列各点在⊙A外的是( )
A.点A B.点B C.点C D.点D
7.直角坐标系的原点为O,⊙O半径为5,点P(4,﹣3)( )
A.在⊙O内 B.在⊙O上 C.在⊙O外 D.无法确定
8.已知⊙O的半径为1,AO=d,且关于x的方程x2﹣2dx+1=0有两个相等的实数根,则点A与⊙O的位置关系是( )
A.在⊙O内 B.在⊙O外 C.在⊙O上 D.无法确定
二.填空题(共8小题)
9.如图,已知⊙A的半径为1,圆心的坐标为(4,3).点P(m,n)是⊙A上的一个动点,则m2+n2的最大值为 .
10.点P是非圆上一点,若点P到⊙O上的点的最小距离是4cm,最大距离是9cm,则⊙O的半径是 .
11.如图,P是以点C(3,0)为圆心,2为半径的圆上的动点,A(0,4),Q是线段PA的中点,连接OQ,则线段OQ的最大值是 .
12.如图,在矩形ABCD中,AB=2,AD=1,以顶点D为圆心作半径为r的圆.若要求另外三个顶点A、B、C中至少有一个点在圆内,且至少有一个点在圆外,则r的取值范围是 .
13.如果圆的半径为4,则弦长x的取值范围是 .
14.在一个边长6cm的正方形里,画一个最大的圆,这个圆的周长是 cm.
15.已知甲圆的直径等于乙圆的半径,且甲乙两圆的面积之和为50cm2,那么甲圆的面积是 cm2.
16.已知⊙O的半径为1,点P到圆心的距离为m,且关于x的一元二次方程x2﹣2x+m=0有两个不相等实数根,则点P与⊙O位置关系是 .
三.解答题(共4小题)
17.如图,△ABC中,∠ACB=90°,BC=5cm,AC=10cm,CD为中线,以C为圆心,以cm长为半径作圆,则点A,B,D与⊙C的位置关系如何?
18.如图,AB、CD为⊙O中两条直径,点E、F在直径CD上,且CE=DF.
求证:AF=BE.
19.如图,BD=OD,∠B=38°,求∠AOD的度数.
20.在矩形ABCD中,AB=3cm,BC=3cm,以点A为圆心AB为半径作圆,则B,C,D三点分别与⊙A有怎样的位置关系?AC的中点M与⊙A又有怎样的位置关系?
参考答案
一.选择题(共8小题)
1.解:∵OP=5>4,
∴点P与⊙O的位置关系是点在圆外.
故选:C.
2.解:∵点A(1,),
∴AO==2,
∵⊙O的半径为2,
∴点A在⊙O上,
故选:A.
3.解:∵⊙O的半径是3,线段OP的长为4,
即点P到圆心的距离大于圆的半径,
∴点P在⊙O外.
故选:C.
4.解:∵圆的半径为6,
∴直径为12,
∵AB是一条弦,
∴AB的长应该小于等于12,不可能为的14,
故选:D.
5.解:∵点B表示实数6,⊙B半径为4.
∴数轴与⊙B的交点表示的数为2或10,
∵点A表示实数a,点A在⊙B内,
∴2<a<10,
故选:B.
6.解:连接AC,
在矩形ABCD中,AB=6,AD=8,
∴BC=AD=8,∠B=90°,
∴AC==10,
∵AB=6<8,AC=10>8,AD=8,
∴点D在⊙A上,点C在⊙A外,点B在⊙A内.
故选:C.
7.解:∵圆心P的坐标为(4,﹣3),
∴OP==5.
∵⊙O的半径为5,
∴点P在⊙O上.
故选:B.
8.解:∵a=1,b=﹣2d,c=1,
∴△=b2﹣4ac=(﹣2d)2﹣4×1×1=4d2﹣4=0,
解得:d=1.
则点A在⊙O上.
故选:C.
二.填空题(共8小题)
9.解:作射线OA交⊙O于P′点,如图,
∵圆心A的坐标为(4,3),点P的坐标为(m,n),
∴OA==5,OP=,
∴m2+n2是点P点圆点的距离的平方,
∴当点P运动到P′处,点P离圆点最远,即m2+n2有最大值,
此时OP=OA+AP′=5+1=6,则m2+n2=36.
故答案为:36.
10.解:分为两种情况:
①当点在圆内时,如图1,
∵点到圆上的最小距离PB=4cm,最大距离PA=9cm,
∴直径AB=4cm+9cm=13cm,
∴半径r=6.5cm;
②当点在圆外时,如图2,
∵点到圆上的最小距离PB=4cm,最大距离PA=9cm,
∴直径AB=9cm﹣4cm=5cm,
∴半径r=2.5cm;
故答案为:6.5cm或2.5cm.
11.解:作点A(0,4)关于x轴的对称点B(0,﹣4),连接BP,
∵Q是线段PA的中点,
∴OQ为△ABP的中位线,
∴OQ=BP,
当BP最大时,OQ最大,
而BP过圆心C时,PB最大,如图,点P运动到P′位置时,BP最大,
∵点C(3,0),
∴OC=3,
∵OB=4,
∴BC==5,
∴BP′=5+2=7,
∴线段OQ的最大值是.
故答案为.
12.解:在直角△ABD中,CD=AB=2,AD=1,
则BD==.
由图可知1<r<.
故答案为:1<r<.
13.解:∵直径为圆中最长的弦,
∴0<x≤8.
故答案为0<x≤8.
14.解:根据题意,最大的圆为正方形的内切圆,
所以最大圆的直径为正方形的边长,
所以这个圆的周长为2π×()=6π(cm).
故答案为6π.
15.解:设乙圆的半径为rcm,则甲圆的半径为 cm,
由圆的面积公式可得:,
解得:πr2=40,
所以甲圆的面积=50﹣40=10(cm2),
故答案为:10.
16.解:∵a=1,b=﹣2,c=m,
∴△=b2﹣4ac=(﹣2)2﹣4×1×m=4﹣4m>0,
解得:m<1.
则点P在⊙O内部.
故答案为:点P在圆内.
三.解答题(共4小题)
17.解:在△ABC中,∠ACB=90°,BC=5cm,AC=10cm,
∴AB==5(cm),
∵CD为中线,
∴CD=AB=cm,
∵AC=10cm>cm,
∴点A在⊙C的外面,
∵BC=5cm<cm,
∴点B在⊙C的内部,
∵CD=cm,
∴点D在⊙C上.
18.解:∵AB、CD为⊙O中两条直径,
∴OA=OB,OC=OD,
∵CE=DF,
∴OE=OF,
在△AOF和△BOE中,
,
∴△AOF≌△BOE(SAS),
∴AF=BE.
19.解:∵BD=OD,∠B=38°,
∴∠DOB=∠B=38°,
∴∠ADO=∠DOB+∠B=2×38°=76°,
∵OA=OD,
∴∠A=∠ADO=76°,
∴∠AOD=180°﹣∠A﹣∠ADO=180°﹣76°﹣76°=28°.
20.解:如图,
观察图象可知,点B在⊙A上,点C,点D在⊙A外.
∵四边形ABCD是矩形,
∴∠ABC=90°,
∵AB=3,BC=3,
∴AC===6,
∴AM=AC=3=AB,
∴点M在⊙A上.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
