《2.5等腰三角形的轴对称性》优生专题提升训练2021-2022学年苏科版八年级数学上册(Word版 含答案)
文档属性
| 名称 | 《2.5等腰三角形的轴对称性》优生专题提升训练2021-2022学年苏科版八年级数学上册(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 299.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-16 11:13:04 | ||
图片预览



文档简介
2021年苏科版八年级数学上册《2.5等腰三角形的轴对称性》优生专题提升训练(附答案)
1.如图,△ABC中,AB=AC,AD⊥BC于点D,DE⊥AB于点E,BF⊥AC于点F,DE=2,则BF的长为( )
A.3 B.4 C.5 D.6
2.如图,每个小方格的边长为1,A,B两点都在小方格的顶点上,点C也是图中小方格的顶点,并且△ABC是等腰三角形,那么点C的个数为( )
A.1 B.2 C.3 D.4
3.如图,AD=BC,AB=AC=BD,∠C=72°,则图中一共有( )个等腰三角形.
A.3 B.4 C.5 D.6
4.如图,在△ABC中,D,E分别在边CB和BC的延长线上,BD=BA,CE=CA,若∠BAC=50°,则∠DAE= .
5.如果等腰三角形的一腰上的高等于腰长的一半,则其一个底角的度数是 .
6.如图,在△ABC中,AB=AC,∠B=36°,点D在线段BC上运动(点D不与点B、C重合),连接AD,作∠ADE=36°,DE交线段AC于点E,点D在运动过程中,若△ADE是等腰三角形,则∠BDA的度数为 .
7.一个等腰三角形的两边长分别是4和9,则周长是 .
8.如图,在△ABC中,∠BAC=90°,点D在BC上,AB=AC,BD=BA,点E在BC的延长线上,CA=CE,连接AE,则∠DAE的度数为 °.
9.如图,在四边形ABCD中,AB=BC,点E为对角线AC与BD的交点,∠AEB=70°,若∠ABC=2∠ADB=4∠CBD,则∠ACD= °.
10.已知P是∠AOB(∠AOB<90°)平分线上一点,点C在射线OA上,且∠OCP=135°,点D在射线OB上运动.若DP=CP,则∠ODP= .
11.如图,在Rt△ABC中,∠C=90°,AF=EF.若∠CFE=72°,则∠B= °.
12.如图,已知△ABC是等边三角形,点B、C、D、E在同一直线上,且CG=CD,DF=DE,则∠E= 度.
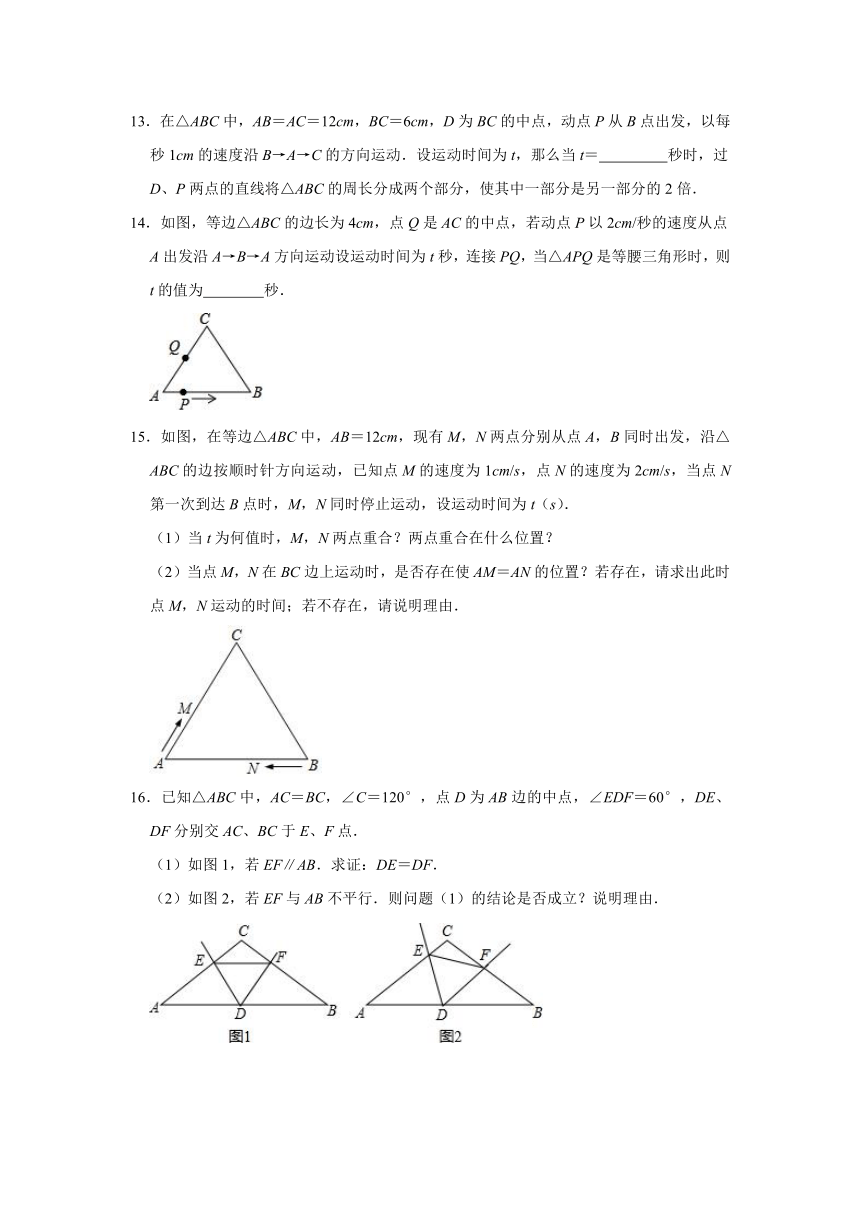
13.在△ABC中,AB=AC=12cm,BC=6cm,D为BC的中点,动点P从B点出发,以每秒1cm的速度沿B→A→C的方向运动.设运动时间为t,那么当t= 秒时,过D、P两点的直线将△ABC的周长分成两个部分,使其中一部分是另一部分的2倍.
14.如图,等边△ABC的边长为4cm,点Q是AC的中点,若动点P以2cm/秒的速度从点A出发沿A→B→A方向运动设运动时间为t秒,连接PQ,当△APQ是等腰三角形时,则t的值为 秒.
15.如图,在等边△ABC中,AB=12cm,现有M,N两点分别从点A,B同时出发,沿△ABC的边按顺时针方向运动,已知点M的速度为1cm/s,点N的速度为2cm/s,当点N第一次到达B点时,M,N同时停止运动,设运动时间为t(s).
(1)当t为何值时,M,N两点重合?两点重合在什么位置?
(2)当点M,N在BC边上运动时,是否存在使AM=AN的位置?若存在,请求出此时点M,N运动的时间;若不存在,请说明理由.
16.已知△ABC中,AC=BC,∠C=120°,点D为AB边的中点,∠EDF=60°,DE、DF分别交AC、BC于E、F点.
(1)如图1,若EF∥AB.求证:DE=DF.
(2)如图2,若EF与AB不平行.则问题(1)的结论是否成立?说明理由.
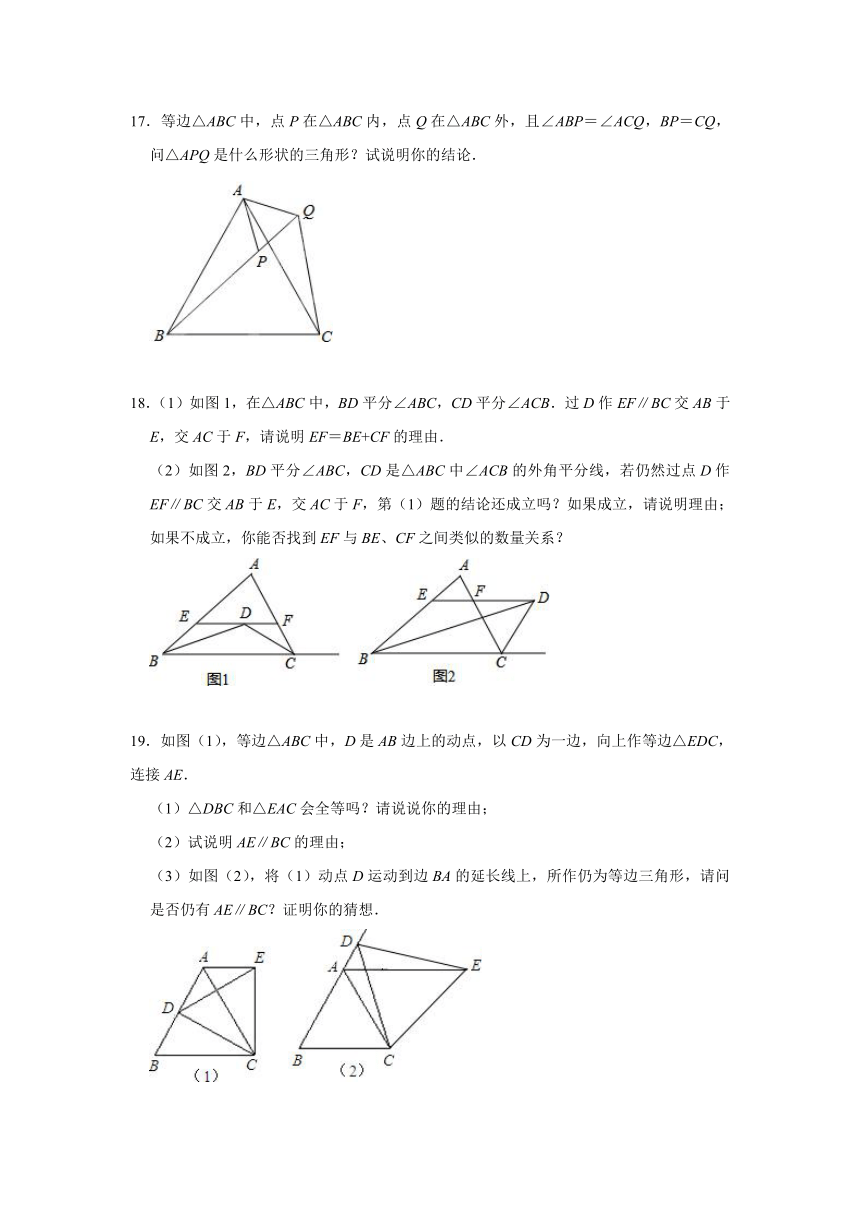
17.等边△ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ,问△APQ是什么形状的三角形?试说明你的结论.
18.(1)如图1,在△ABC中,BD平分∠ABC,CD平分∠ACB.过D作EF∥BC交AB于E,交AC于F,请说明EF=BE+CF的理由.
(2)如图2,BD平分∠ABC,CD是△ABC中∠ACB的外角平分线,若仍然过点D作EF∥BC交AB于E,交AC于F,第(1)题的结论还成立吗?如果成立,请说明理由;如果不成立,你能否找到EF与BE、CF之间类似的数量关系?
19.如图(1),等边△ABC中,D是AB边上的动点,以CD为一边,向上作等边△EDC,连接AE.
(1)△DBC和△EAC会全等吗?请说说你的理由;
(2)试说明AE∥BC的理由;
(3)如图(2),将(1)动点D运动到边BA的延长线上,所作仍为等边三角形,请问是否仍有AE∥BC?证明你的猜想.
20.如图,在等边△ABC中,边AB=6厘米,若动点P从点C开始,按C→B→A→C的路径运动,且速度为1厘米/秒,设点P的运动时间为t秒.
(1)当t=3时,判断AP与BC的位置关系,并说明理由;
(2)当△PBC的面积为△ABC面积的一半时,求t的值;
(3)另有一点Q,从点C开始,按C→A→B→C的路径运动,且速度为1.5厘米/秒,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动.当t为何值时,直线PQ把△ABC的周长分成相等的两部分.
参考答案
1.解:∵△ABC中,AB=AC,AD⊥BC,
∴AD是△ABC的中线,
∴S△ABC=2S△ABD=2×AB?DE=AB?DE=2AB,
∵S△ABC=AC?BF,
∴AC?BF=2AB,
∵AC=AB,
∴BF=2,
∴BF=4,
故选:B.
2.解:当AB为腰时,点C的个数有2个;
当AB为底时,点C的个数有1个,
故选:C.
3.解:∵AB=AC=BD,
∴△ABD与△BAC是等腰三角形,
在△ABD与△BAC中,
,
∴△ABD≌△BAC(SSS),
∴∠D=∠C=72°,
∴∠BAD=∠D=∠C=∠ABC=72°,
∴∠∠ABD=∠BAC=36°,
∴∠DAE=∠CBE=32°,
∴∠AED=∠BEC=72°,
∴∠D=∠AED=∠C=∠BE,
∴△ADE和△BCE是等腰三角形,
∵∠AED=∠BEC,
∴△ADE≌△BCE(AAS),
∴AE=BE,
∴△ABE是等腰三角形,
故选:C.
4.解:∵AB=BD,AC=CE,
∴∠BAD=∠BDA,∠E=∠CAE,
设∠BAD=∠BDA=x,∠E=∠CAE=y,
∴∠ABC=∠BAD+∠BDA=2x,∠ACB=∠E+∠CAE=2y,
∵∠ABC+∠ACB+∠BAC=180°,
∴2x+2y+50°=180°,
∴x+y=65°,
∴∠DAE=∠DAB+∠CAE+∠BAC=65°+50°=115°.
故答案为:115°.
5.解:如图①:∵CD⊥AB,
∴∠ADC=90°,
∵CD=AC,
∴∠A=30°,
∵AB=AC,
∴∠B=∠ACB==75°;
如图②:∵CD⊥AB,
∴∠ADC=90°,
∵CD=AC,
∴∠CAD=30°,
∵AB=AC,
∴∠B=∠ACB,
∴∠DAC=∠B+∠ACB=2∠B=30°,
∴∠B=∠ACB=15°.
综上,这个三角形的底角为:75°或15°.
故答案为:15°或75°.
6.解:∵AB=AC,
∴∠B=∠C=36°,
①当AD=AE时,∠ADE=∠AED=36°,
∵∠AED>∠C,
∴此时不符合;
②当DA=DE时,即∠DAE=∠DEA=×(180°﹣36°)=72°,
∵∠BAC=180°﹣36°﹣36°=108°,
∴∠BAD=108°﹣72°=36°;
∴∠BDA=180°﹣36°﹣36°=108°;
③当EA=ED时,∠ADE=∠DAE=36°,
∴∠BAD=108°﹣36°=72°,
∴∠BDA=180°﹣72°﹣36°=72°;
∴当△ADE是等腰三角形时,∠BDA的度数是108°或72°.
故答案为:108°或72°.
7.解:当等腰三角形的腰为4时,三边为4,4,9,4+4<9,三边关系不成立,
当等腰三角形的腰为9时,三边为4,9,9,三边关系成立,周长为4+9+9=22.
故答案为:22.
8.解:∵AB=AC,∠BAC=90°,
∴∠B=∠ACB=45°,
∵BD=BA,
∴∠BAD=∠BDA=(180°﹣∠B)=67.5°,
∵CE=CA,
∴∠CAE=∠E=∠ACB=22.5°,
在△ABE中,∠BAE=180°﹣∠B﹣∠E=112.5°,
∴∠DAE=∠BAE﹣∠BAD=112.5°﹣67.5°=45°,
故答案为:45.
9.解:设∠CBD=x,
由题意得:∠ABC=2∠ADB=4∠CBD=4x,
∵AB=BC,
∴∠BAC=∠ACB=(180°﹣4x)=90°﹣2x,
∵∠ABE+∠BAE+∠AEB=180°,
∴3x+90°﹣2x+70°=180°
∴x=20°,
∴∠CBD=20°,∠ADB=40°,∠ABC=80°,
∴∠ABD=∠ABC﹣∠CBD=60°,
在BD上取一点F使BF=BA,延长AF交BC的延长线于点G,连接DG,
∴△ABF是等边三角形,
∴AF=BF,∠BAF=∠AFB=60°,
∵∠BAD=180°﹣∠ABD﹣∠ADB=80°,
∴∠DAF=∠BAD﹣∠BAF=20°,
∴∠DAF=∠CBD=∠CBF,
在△ADF和△BGF中,
,
∴△ADF≌△BGF(ASA),
∴FD=FG,
∵∠DFG=∠AFB=60°,
∴△DFG是等边三角形,
∴DF=DG,
连接CF,
∴△BCF为等腰三角形,
∴∠BFC=,
∴∠CFG=180°﹣∠AFB﹣∠BFC=40°,
∵∠CGF=∠BFA﹣∠DBC=40°,
∴∠CFG=∠CGF,
∴CF=CG,
∵DF=DG,DC=DC,
∴△DFC≌△DGC,
∴∠FDC=∠GDC==30°,
∵∠DEC=∠AEB=70°,
∴∠ACD=180°﹣∠DEC﹣∠FDC=80°,
故答案为:80.
10.解:如图,过P作PM⊥OB于M,PN⊥OA于N,
又∵P是∠AOB(∠AOB<90°)平分线上一点,
∴PM=PN.
在Rt△PMD与Rt△PNC中,
,
∴Rt△PMD≌Rt△PNC(HL),
∴∠PDM=∠PCN.
∵∠OCP=135°,
∴∠PCN=45°,
∴∠PDM=45°,
当D落在D1的位置时,∠ODP=135°;
当D落在D2的位置时,∠ODP=45°.
即∠ODP=135°或45°.
故答案为:135°或45°.
11.解:∵AF=EF,
∴∠A=∠AEF,
∵∠A+∠AEF=∠CFE=72°,
∴∠A=×72°=36°,
在Rt△ABC中,∠A=36°,
∴∠B=90°﹣36°=54°.
故答案为:54.
12.解:∵△ABC是等边三角形,
∴∠ACB=60°,∠ACD=120°,
∵CG=CD,
∴∠CDG=30°,∠FDE=150°,
∵DF=DE,
∴∠E=15°.
故答案为:15.
13.解:分两种情况:
(1)P点在AB上时,如图,
∵AB=AC=12cm,BD=CD=BC=×6=3cm,
设P点运动了t秒,则BP=t,AP=12﹣t,由题意得:
BP+BD=(AP+AC+CD)或(BP+BD)=AP+AC+CD,
∴t+3=(12﹣t+12+3)①或(t+3)=12﹣t+12+3②,
解①得t=7秒,解②得,t=17(舍去);
(2)P点在AC上时,如图,
∵AB=AC=12cm,BD=CD=BC=×6=3cm,P点运动了t秒,
则AB+AP=t,PC=AB+AC﹣t=24﹣t,
由题意得:BD+AB+AP=2(PC+CD)或2(BD+AB+AP)=PC+CD,
∴3+t=2(24﹣t+3)①或2(3+t)=24﹣t+3②
解①得t=17秒,解②得,t=7秒(舍去).
故当t=7或17秒时,过D、P两点的直线将△ABC的周长分成两个部分,使其中一部分是另一部分的2倍.
故答案为:7或17.
14.解:如图,连接PQ,
∵△ABC是等边三角形,
∴∠A=60°,
∵△APQ是等腰三角形,
∴△APQ是等边三角形,
又∵Q是AC的中点,
∴AQ=AP=2cm,
分两种情况:
①当点P由A向B运动时,t===1(秒);
②当点P由B向A运动时,t===3(秒);
综上所述,当△APQ是等腰三角形时,则t的值为1或3秒.
故答案为:1或3.
15.解:(1)由题意,t×1+12=2t,
解得:t=12,
∴当t=12时,M,N两点重合,
此时两点在点C处重合;
(2)结论:当点M、N在BC边上运动时,可以得到以MN为底边的等腰三角形.
理由:由(1)知12秒时M、N两点重合,恰好在C处,
如图,假设△AMN是等腰三角形,
∴AN=AM,
∴∠AMN=∠ANM,
∴∠AMC=∠ANB,
∵△ACB是等边三角形,
∴∠C=∠B,
在△ACM和△ABN中,
,
∴△ACM≌△ABN(AAS),
∴CM=BN,
设当点M、N在BC边上运动时,M、N运动的时间y秒时,△AMN是等腰三角形,
∴CM=y﹣12,NB=36﹣2y,
∵CM=NB,
∴y﹣12=36﹣2y,
解得:y=16.故假设成立.
∴当点M、N在BC边上运动时,当运动时间为12秒或16秒时,AM=AN.
16.解:(1)∵EF∥AB.
∴∠FEC=∠A=30°.
∠EFC=∠B=30°
∴EC=CF.
又∵AC=BC
∴AE=BF
D是AB中点.
∴DB=AD
∴△ADE≌△BDF.
∴DE=DF
(2)过D作DM⊥AC交AC于M,再作DN⊥BC交BC于N.
∵AC=BC,
∴∠A=∠B,
又∵∠ACB=120°,
∴∠A=∠B=(180°﹣∠ACB)÷2=30°,
∴∠ADM=∠BDN=60°,
∴∠MDN=180°﹣∠ADM﹣∠BDN=60°.
∵AC=BC、AD=BD,
∴∠ACD=∠BCD,
∴DM=DN.
由∠MDN=60°、∠EDF=60°,可知:
一、当M与E重合时,N就一定与F重合.此时:
DM=DE、DN=DF,结合证得的DM=DN,得:DE=DF,但EF∥AB,不合题意.
二、当M落在C、E之间时,N就一定落在B、F之间.此时:
∠EDM=∠EDF﹣∠MDF=60°﹣∠MDF,
∠FDN=∠MDN﹣∠MDF=60°﹣∠MDF,
∴∠EDM=∠FDN,
又∵∠DME=∠DNF=90°、DM=DN,
∴△DEM≌△DFN(ASA),
∴DE=DF.
三、当M落在A、E之间时,N就一定落在C、F之间.此时:
∠EDM=∠MDN﹣∠EDN=60°﹣∠EDN,
∠FDN=∠EDF﹣∠EDN=60°﹣∠EDN,
∴∠EDM=∠FDN,
又∵∠DME=∠DNF=90°、DM=DN,
∴△DEM≌△DFN(ASA),
∴DE=DF.
综上一、二、三所述,得:DE=DF.
17.解:△APQ为等边三角形.
证明:∵△ABC为等边三角形,
∴AB=AC.
在△ABP与△ACQ中,
∵,
∴△ABP≌△ACQ(SAS).
∴AP=AQ,∠BAP=∠CAQ.
∵∠BAC=∠BAP+∠PAC=60°,
∴∠PAQ=∠CAQ+∠PAC=60°,
∴△APQ是等边三角形.
18.(1)∵在△ABC中,BD平分∠ABC,CD平分∠ACB,
∴∠EBD=∠DBC,∠DCB=∠FCD.
又∵EF∥BC交AB于E,交AC于F,
∴∠EDB=∠DBC,∠FDC=∠DCB
∴∠EBD=∠EDB,∠FDC=∠FCD,
∴BE=ED,CF=FD,
∴EF=ED+DF=BE+CF.
即:EF=BE+CF.
(2)不成立.EF=BE﹣CF.理由如下(如图):
∵BD平分∠ABC,CD是△ABC中∠ACB的外角平分线
∠EBD=∠DBC,∠FCD=∠DCG
∵EF∥BC交AB于E,交AC于F,
∴∠EDB=∠DBC,∠FDC=∠DCG,
∴∠EBD=∠EDB,∠FDC=∠FCD,
∴BE=DE,DF=CF,
∴EF=BE﹣CF.
19.解:(1)△DBC和△EAC会全等
证明:∵∠ACB=60°,∠DCE=60°
∴∠BCD=60°﹣∠ACD,∠ACE=60°﹣∠ACD
∴∠BCD=∠ACE
在△DBC和△EAC中,
∵,
∴△DBC≌△EAC(SAS),
(2)∵△DBC≌△EAC
∴∠EAC=∠B=60°
又∠ACB=60°
∴∠EAC=∠ACB
∴AE∥BC
(3)结论:AE∥BC
理由:∵△ABC、△EDC为等边三角形
∴BC=AC,DC=CE,∠BCA=∠DCE=60°
∠BCA+∠ACD=∠DCE+∠ACD,即∠BCD=∠ACE
在△DBC和△EAC中,
∵,
∴△DBC≌△EAC(SAS),
∴∠EAC=∠B=60°
又∵∠ACB=60°
∴∠EAC=∠ACB
∴AE∥BC.
20.解:(1)判断:AP⊥BC,
理由如下:如图1,
∵t=3,
∴BP=CP=3,
∵AB=AC,
∴AP⊥BC;
(2)当△PBC的面积为△ABC面积的一半时,点P为AB中点或点P为AC中点,则CB+CP=9或CB+BA+CP=15,
∴t=9或t=15,
∴当△PBC的面积为△ABC面积的一半时,t的值为9或15;
(3)当点P在边BC上,且点Q在边AC上时,CP=t,CQ=1.5t
则t+1.5t=9,
∴t=3.6,
当点P在边AB上,且点Q在边BC上时,BP=t﹣6,BQ=1.5t﹣12,
则t﹣6+1.5t﹣12=9,
∴t=10.8,
所以当t为3.6或10.8秒时,直线PQ把△ABC的周长分成相等的两部分.
1.如图,△ABC中,AB=AC,AD⊥BC于点D,DE⊥AB于点E,BF⊥AC于点F,DE=2,则BF的长为( )
A.3 B.4 C.5 D.6
2.如图,每个小方格的边长为1,A,B两点都在小方格的顶点上,点C也是图中小方格的顶点,并且△ABC是等腰三角形,那么点C的个数为( )
A.1 B.2 C.3 D.4
3.如图,AD=BC,AB=AC=BD,∠C=72°,则图中一共有( )个等腰三角形.
A.3 B.4 C.5 D.6
4.如图,在△ABC中,D,E分别在边CB和BC的延长线上,BD=BA,CE=CA,若∠BAC=50°,则∠DAE= .
5.如果等腰三角形的一腰上的高等于腰长的一半,则其一个底角的度数是 .
6.如图,在△ABC中,AB=AC,∠B=36°,点D在线段BC上运动(点D不与点B、C重合),连接AD,作∠ADE=36°,DE交线段AC于点E,点D在运动过程中,若△ADE是等腰三角形,则∠BDA的度数为 .
7.一个等腰三角形的两边长分别是4和9,则周长是 .
8.如图,在△ABC中,∠BAC=90°,点D在BC上,AB=AC,BD=BA,点E在BC的延长线上,CA=CE,连接AE,则∠DAE的度数为 °.
9.如图,在四边形ABCD中,AB=BC,点E为对角线AC与BD的交点,∠AEB=70°,若∠ABC=2∠ADB=4∠CBD,则∠ACD= °.
10.已知P是∠AOB(∠AOB<90°)平分线上一点,点C在射线OA上,且∠OCP=135°,点D在射线OB上运动.若DP=CP,则∠ODP= .
11.如图,在Rt△ABC中,∠C=90°,AF=EF.若∠CFE=72°,则∠B= °.
12.如图,已知△ABC是等边三角形,点B、C、D、E在同一直线上,且CG=CD,DF=DE,则∠E= 度.
13.在△ABC中,AB=AC=12cm,BC=6cm,D为BC的中点,动点P从B点出发,以每秒1cm的速度沿B→A→C的方向运动.设运动时间为t,那么当t= 秒时,过D、P两点的直线将△ABC的周长分成两个部分,使其中一部分是另一部分的2倍.
14.如图,等边△ABC的边长为4cm,点Q是AC的中点,若动点P以2cm/秒的速度从点A出发沿A→B→A方向运动设运动时间为t秒,连接PQ,当△APQ是等腰三角形时,则t的值为 秒.
15.如图,在等边△ABC中,AB=12cm,现有M,N两点分别从点A,B同时出发,沿△ABC的边按顺时针方向运动,已知点M的速度为1cm/s,点N的速度为2cm/s,当点N第一次到达B点时,M,N同时停止运动,设运动时间为t(s).
(1)当t为何值时,M,N两点重合?两点重合在什么位置?
(2)当点M,N在BC边上运动时,是否存在使AM=AN的位置?若存在,请求出此时点M,N运动的时间;若不存在,请说明理由.
16.已知△ABC中,AC=BC,∠C=120°,点D为AB边的中点,∠EDF=60°,DE、DF分别交AC、BC于E、F点.
(1)如图1,若EF∥AB.求证:DE=DF.
(2)如图2,若EF与AB不平行.则问题(1)的结论是否成立?说明理由.
17.等边△ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ,问△APQ是什么形状的三角形?试说明你的结论.
18.(1)如图1,在△ABC中,BD平分∠ABC,CD平分∠ACB.过D作EF∥BC交AB于E,交AC于F,请说明EF=BE+CF的理由.
(2)如图2,BD平分∠ABC,CD是△ABC中∠ACB的外角平分线,若仍然过点D作EF∥BC交AB于E,交AC于F,第(1)题的结论还成立吗?如果成立,请说明理由;如果不成立,你能否找到EF与BE、CF之间类似的数量关系?
19.如图(1),等边△ABC中,D是AB边上的动点,以CD为一边,向上作等边△EDC,连接AE.
(1)△DBC和△EAC会全等吗?请说说你的理由;
(2)试说明AE∥BC的理由;
(3)如图(2),将(1)动点D运动到边BA的延长线上,所作仍为等边三角形,请问是否仍有AE∥BC?证明你的猜想.
20.如图,在等边△ABC中,边AB=6厘米,若动点P从点C开始,按C→B→A→C的路径运动,且速度为1厘米/秒,设点P的运动时间为t秒.
(1)当t=3时,判断AP与BC的位置关系,并说明理由;
(2)当△PBC的面积为△ABC面积的一半时,求t的值;
(3)另有一点Q,从点C开始,按C→A→B→C的路径运动,且速度为1.5厘米/秒,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动.当t为何值时,直线PQ把△ABC的周长分成相等的两部分.
参考答案
1.解:∵△ABC中,AB=AC,AD⊥BC,
∴AD是△ABC的中线,
∴S△ABC=2S△ABD=2×AB?DE=AB?DE=2AB,
∵S△ABC=AC?BF,
∴AC?BF=2AB,
∵AC=AB,
∴BF=2,
∴BF=4,
故选:B.
2.解:当AB为腰时,点C的个数有2个;
当AB为底时,点C的个数有1个,
故选:C.
3.解:∵AB=AC=BD,
∴△ABD与△BAC是等腰三角形,
在△ABD与△BAC中,
,
∴△ABD≌△BAC(SSS),
∴∠D=∠C=72°,
∴∠BAD=∠D=∠C=∠ABC=72°,
∴∠∠ABD=∠BAC=36°,
∴∠DAE=∠CBE=32°,
∴∠AED=∠BEC=72°,
∴∠D=∠AED=∠C=∠BE,
∴△ADE和△BCE是等腰三角形,
∵∠AED=∠BEC,
∴△ADE≌△BCE(AAS),
∴AE=BE,
∴△ABE是等腰三角形,
故选:C.
4.解:∵AB=BD,AC=CE,
∴∠BAD=∠BDA,∠E=∠CAE,
设∠BAD=∠BDA=x,∠E=∠CAE=y,
∴∠ABC=∠BAD+∠BDA=2x,∠ACB=∠E+∠CAE=2y,
∵∠ABC+∠ACB+∠BAC=180°,
∴2x+2y+50°=180°,
∴x+y=65°,
∴∠DAE=∠DAB+∠CAE+∠BAC=65°+50°=115°.
故答案为:115°.
5.解:如图①:∵CD⊥AB,
∴∠ADC=90°,
∵CD=AC,
∴∠A=30°,
∵AB=AC,
∴∠B=∠ACB==75°;
如图②:∵CD⊥AB,
∴∠ADC=90°,
∵CD=AC,
∴∠CAD=30°,
∵AB=AC,
∴∠B=∠ACB,
∴∠DAC=∠B+∠ACB=2∠B=30°,
∴∠B=∠ACB=15°.
综上,这个三角形的底角为:75°或15°.
故答案为:15°或75°.
6.解:∵AB=AC,
∴∠B=∠C=36°,
①当AD=AE时,∠ADE=∠AED=36°,
∵∠AED>∠C,
∴此时不符合;
②当DA=DE时,即∠DAE=∠DEA=×(180°﹣36°)=72°,
∵∠BAC=180°﹣36°﹣36°=108°,
∴∠BAD=108°﹣72°=36°;
∴∠BDA=180°﹣36°﹣36°=108°;
③当EA=ED时,∠ADE=∠DAE=36°,
∴∠BAD=108°﹣36°=72°,
∴∠BDA=180°﹣72°﹣36°=72°;
∴当△ADE是等腰三角形时,∠BDA的度数是108°或72°.
故答案为:108°或72°.
7.解:当等腰三角形的腰为4时,三边为4,4,9,4+4<9,三边关系不成立,
当等腰三角形的腰为9时,三边为4,9,9,三边关系成立,周长为4+9+9=22.
故答案为:22.
8.解:∵AB=AC,∠BAC=90°,
∴∠B=∠ACB=45°,
∵BD=BA,
∴∠BAD=∠BDA=(180°﹣∠B)=67.5°,
∵CE=CA,
∴∠CAE=∠E=∠ACB=22.5°,
在△ABE中,∠BAE=180°﹣∠B﹣∠E=112.5°,
∴∠DAE=∠BAE﹣∠BAD=112.5°﹣67.5°=45°,
故答案为:45.
9.解:设∠CBD=x,
由题意得:∠ABC=2∠ADB=4∠CBD=4x,
∵AB=BC,
∴∠BAC=∠ACB=(180°﹣4x)=90°﹣2x,
∵∠ABE+∠BAE+∠AEB=180°,
∴3x+90°﹣2x+70°=180°
∴x=20°,
∴∠CBD=20°,∠ADB=40°,∠ABC=80°,
∴∠ABD=∠ABC﹣∠CBD=60°,
在BD上取一点F使BF=BA,延长AF交BC的延长线于点G,连接DG,
∴△ABF是等边三角形,
∴AF=BF,∠BAF=∠AFB=60°,
∵∠BAD=180°﹣∠ABD﹣∠ADB=80°,
∴∠DAF=∠BAD﹣∠BAF=20°,
∴∠DAF=∠CBD=∠CBF,
在△ADF和△BGF中,
,
∴△ADF≌△BGF(ASA),
∴FD=FG,
∵∠DFG=∠AFB=60°,
∴△DFG是等边三角形,
∴DF=DG,
连接CF,
∴△BCF为等腰三角形,
∴∠BFC=,
∴∠CFG=180°﹣∠AFB﹣∠BFC=40°,
∵∠CGF=∠BFA﹣∠DBC=40°,
∴∠CFG=∠CGF,
∴CF=CG,
∵DF=DG,DC=DC,
∴△DFC≌△DGC,
∴∠FDC=∠GDC==30°,
∵∠DEC=∠AEB=70°,
∴∠ACD=180°﹣∠DEC﹣∠FDC=80°,
故答案为:80.
10.解:如图,过P作PM⊥OB于M,PN⊥OA于N,
又∵P是∠AOB(∠AOB<90°)平分线上一点,
∴PM=PN.
在Rt△PMD与Rt△PNC中,
,
∴Rt△PMD≌Rt△PNC(HL),
∴∠PDM=∠PCN.
∵∠OCP=135°,
∴∠PCN=45°,
∴∠PDM=45°,
当D落在D1的位置时,∠ODP=135°;
当D落在D2的位置时,∠ODP=45°.
即∠ODP=135°或45°.
故答案为:135°或45°.
11.解:∵AF=EF,
∴∠A=∠AEF,
∵∠A+∠AEF=∠CFE=72°,
∴∠A=×72°=36°,
在Rt△ABC中,∠A=36°,
∴∠B=90°﹣36°=54°.
故答案为:54.
12.解:∵△ABC是等边三角形,
∴∠ACB=60°,∠ACD=120°,
∵CG=CD,
∴∠CDG=30°,∠FDE=150°,
∵DF=DE,
∴∠E=15°.
故答案为:15.
13.解:分两种情况:
(1)P点在AB上时,如图,
∵AB=AC=12cm,BD=CD=BC=×6=3cm,
设P点运动了t秒,则BP=t,AP=12﹣t,由题意得:
BP+BD=(AP+AC+CD)或(BP+BD)=AP+AC+CD,
∴t+3=(12﹣t+12+3)①或(t+3)=12﹣t+12+3②,
解①得t=7秒,解②得,t=17(舍去);
(2)P点在AC上时,如图,
∵AB=AC=12cm,BD=CD=BC=×6=3cm,P点运动了t秒,
则AB+AP=t,PC=AB+AC﹣t=24﹣t,
由题意得:BD+AB+AP=2(PC+CD)或2(BD+AB+AP)=PC+CD,
∴3+t=2(24﹣t+3)①或2(3+t)=24﹣t+3②
解①得t=17秒,解②得,t=7秒(舍去).
故当t=7或17秒时,过D、P两点的直线将△ABC的周长分成两个部分,使其中一部分是另一部分的2倍.
故答案为:7或17.
14.解:如图,连接PQ,
∵△ABC是等边三角形,
∴∠A=60°,
∵△APQ是等腰三角形,
∴△APQ是等边三角形,
又∵Q是AC的中点,
∴AQ=AP=2cm,
分两种情况:
①当点P由A向B运动时,t===1(秒);
②当点P由B向A运动时,t===3(秒);
综上所述,当△APQ是等腰三角形时,则t的值为1或3秒.
故答案为:1或3.
15.解:(1)由题意,t×1+12=2t,
解得:t=12,
∴当t=12时,M,N两点重合,
此时两点在点C处重合;
(2)结论:当点M、N在BC边上运动时,可以得到以MN为底边的等腰三角形.
理由:由(1)知12秒时M、N两点重合,恰好在C处,
如图,假设△AMN是等腰三角形,
∴AN=AM,
∴∠AMN=∠ANM,
∴∠AMC=∠ANB,
∵△ACB是等边三角形,
∴∠C=∠B,
在△ACM和△ABN中,
,
∴△ACM≌△ABN(AAS),
∴CM=BN,
设当点M、N在BC边上运动时,M、N运动的时间y秒时,△AMN是等腰三角形,
∴CM=y﹣12,NB=36﹣2y,
∵CM=NB,
∴y﹣12=36﹣2y,
解得:y=16.故假设成立.
∴当点M、N在BC边上运动时,当运动时间为12秒或16秒时,AM=AN.
16.解:(1)∵EF∥AB.
∴∠FEC=∠A=30°.
∠EFC=∠B=30°
∴EC=CF.
又∵AC=BC
∴AE=BF
D是AB中点.
∴DB=AD
∴△ADE≌△BDF.
∴DE=DF
(2)过D作DM⊥AC交AC于M,再作DN⊥BC交BC于N.
∵AC=BC,
∴∠A=∠B,
又∵∠ACB=120°,
∴∠A=∠B=(180°﹣∠ACB)÷2=30°,
∴∠ADM=∠BDN=60°,
∴∠MDN=180°﹣∠ADM﹣∠BDN=60°.
∵AC=BC、AD=BD,
∴∠ACD=∠BCD,
∴DM=DN.
由∠MDN=60°、∠EDF=60°,可知:
一、当M与E重合时,N就一定与F重合.此时:
DM=DE、DN=DF,结合证得的DM=DN,得:DE=DF,但EF∥AB,不合题意.
二、当M落在C、E之间时,N就一定落在B、F之间.此时:
∠EDM=∠EDF﹣∠MDF=60°﹣∠MDF,
∠FDN=∠MDN﹣∠MDF=60°﹣∠MDF,
∴∠EDM=∠FDN,
又∵∠DME=∠DNF=90°、DM=DN,
∴△DEM≌△DFN(ASA),
∴DE=DF.
三、当M落在A、E之间时,N就一定落在C、F之间.此时:
∠EDM=∠MDN﹣∠EDN=60°﹣∠EDN,
∠FDN=∠EDF﹣∠EDN=60°﹣∠EDN,
∴∠EDM=∠FDN,
又∵∠DME=∠DNF=90°、DM=DN,
∴△DEM≌△DFN(ASA),
∴DE=DF.
综上一、二、三所述,得:DE=DF.
17.解:△APQ为等边三角形.
证明:∵△ABC为等边三角形,
∴AB=AC.
在△ABP与△ACQ中,
∵,
∴△ABP≌△ACQ(SAS).
∴AP=AQ,∠BAP=∠CAQ.
∵∠BAC=∠BAP+∠PAC=60°,
∴∠PAQ=∠CAQ+∠PAC=60°,
∴△APQ是等边三角形.
18.(1)∵在△ABC中,BD平分∠ABC,CD平分∠ACB,
∴∠EBD=∠DBC,∠DCB=∠FCD.
又∵EF∥BC交AB于E,交AC于F,
∴∠EDB=∠DBC,∠FDC=∠DCB
∴∠EBD=∠EDB,∠FDC=∠FCD,
∴BE=ED,CF=FD,
∴EF=ED+DF=BE+CF.
即:EF=BE+CF.
(2)不成立.EF=BE﹣CF.理由如下(如图):
∵BD平分∠ABC,CD是△ABC中∠ACB的外角平分线
∠EBD=∠DBC,∠FCD=∠DCG
∵EF∥BC交AB于E,交AC于F,
∴∠EDB=∠DBC,∠FDC=∠DCG,
∴∠EBD=∠EDB,∠FDC=∠FCD,
∴BE=DE,DF=CF,
∴EF=BE﹣CF.
19.解:(1)△DBC和△EAC会全等
证明:∵∠ACB=60°,∠DCE=60°
∴∠BCD=60°﹣∠ACD,∠ACE=60°﹣∠ACD
∴∠BCD=∠ACE
在△DBC和△EAC中,
∵,
∴△DBC≌△EAC(SAS),
(2)∵△DBC≌△EAC
∴∠EAC=∠B=60°
又∠ACB=60°
∴∠EAC=∠ACB
∴AE∥BC
(3)结论:AE∥BC
理由:∵△ABC、△EDC为等边三角形
∴BC=AC,DC=CE,∠BCA=∠DCE=60°
∠BCA+∠ACD=∠DCE+∠ACD,即∠BCD=∠ACE
在△DBC和△EAC中,
∵,
∴△DBC≌△EAC(SAS),
∴∠EAC=∠B=60°
又∵∠ACB=60°
∴∠EAC=∠ACB
∴AE∥BC.
20.解:(1)判断:AP⊥BC,
理由如下:如图1,
∵t=3,
∴BP=CP=3,
∵AB=AC,
∴AP⊥BC;
(2)当△PBC的面积为△ABC面积的一半时,点P为AB中点或点P为AC中点,则CB+CP=9或CB+BA+CP=15,
∴t=9或t=15,
∴当△PBC的面积为△ABC面积的一半时,t的值为9或15;
(3)当点P在边BC上,且点Q在边AC上时,CP=t,CQ=1.5t
则t+1.5t=9,
∴t=3.6,
当点P在边AB上,且点Q在边BC上时,BP=t﹣6,BQ=1.5t﹣12,
则t﹣6+1.5t﹣12=9,
∴t=10.8,
所以当t为3.6或10.8秒时,直线PQ把△ABC的周长分成相等的两部分.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
