《2.8圆锥的侧面积》能力达标专题突破训练(附答案)2021-2022学年九年级数学苏科版上册
文档属性
| 名称 | 《2.8圆锥的侧面积》能力达标专题突破训练(附答案)2021-2022学年九年级数学苏科版上册 |  | |
| 格式 | doc | ||
| 文件大小 | 238.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-16 11:29:20 | ||
图片预览




文档简介
2021-2022学年苏科版九年级数学上册《2.8圆锥的侧面积》
能力达标专题突破训练(附答案)
1.用半径为30cm,圆心角为120°的扇形纸片恰好能围成一个圆锥的侧面,则这个圆锥底面半径为( )
A.5cm B.10cm C.15cm D.20cm
2.如图,从一块直径是2的圆形铁片上剪出一个圆心角为90°的扇形,将剪下来的扇形围成一个圆锥.那么这个圆锥的底面圆的半径是( )
A. B. C. D.1
3.如图,已知扇形OAB的半径为6cm,圆心角的度数为120°,若将OA,OB重合后围成一圆锥侧面,那么圆锥的底面半径为( )
A.2cm B.3cm C.6cm D.2cm
4.用一个圆心角为120°,半径为6的扇形做成一个圆锥的侧面,则这个圆锥的底面圆的半径为( )
A.2 B.6 C.2 D.3
5.一个圆锥的侧面展开图是一个面积为的半圆,则该圆锥的高为( )
A..1 B.2 C. D.
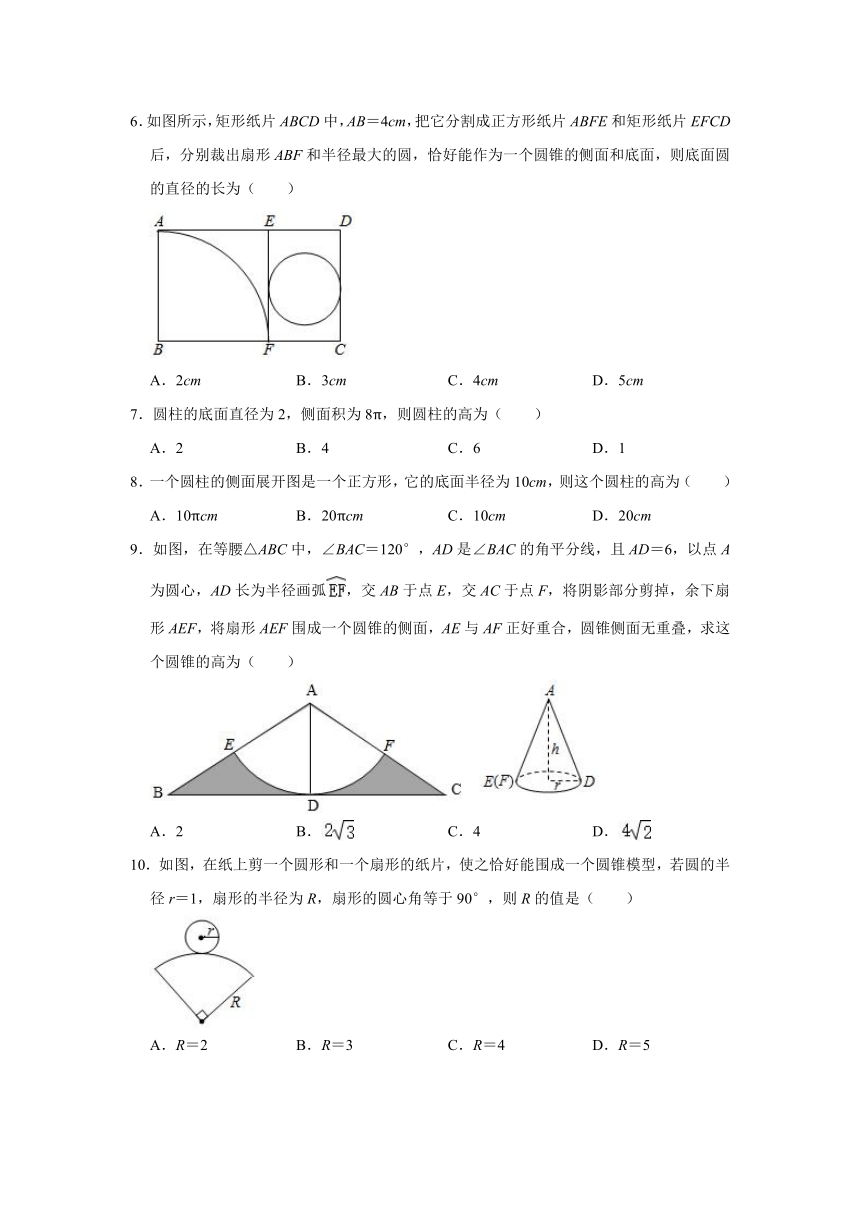
6.如图所示,矩形纸片ABCD中,AB=4cm,把它分割成正方形纸片ABFE和矩形纸片EFCD后,分别裁出扇形ABF和半径最大的圆,恰好能作为一个圆锥的侧面和底面,则底面圆的直径的长为( )
A.2cm B.3cm C.4cm D.5cm
7.圆柱的底面直径为2,侧面积为8π,则圆柱的高为( )
A.2 B.4 C.6 D.1
8.一个圆柱的侧面展开图是一个正方形,它的底面半径为10cm,则这个圆柱的高为( )
A.10πcm B.20πcm C.10cm D.20cm
9.如图,在等腰△ABC中,∠BAC=120°,AD是∠BAC的角平分线,且AD=6,以点A为圆心,AD长为半径画弧,交AB于点E,交AC于点F,将阴影部分剪掉,余下扇形AEF,将扇形AEF围成一个圆锥的侧面,AE与AF正好重合,圆锥侧面无重叠,求这个圆锥的高为( )
A.2 B. C.4 D.
10.如图,在纸上剪一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型,若圆的半径r=1,扇形的半径为R,扇形的圆心角等于90°,则R的值是( )
A.R=2 B.R=3 C.R=4 D.R=5
11.如图是某几何体的三种视图,其表面积为( )
A.2π B.3π C.4π D.5π
12.某同学在数学实践活动中,制作了一个侧面积为60π,底面半径为6的圆锥模型(如图所示),则此圆锥的母线长为 .
13.用半径为50,圆心角为120°的扇形纸片围成一个圆锥的侧面,则这个圆锥的底面半径为 .
14.圆锥形的烟囱冒的底面直径是80cm,母线长是50cm,制作100个这样的烟囱冒至少需要 cm2的铁皮(结果保留π).
15.如图所示,已知扇形AOB的半径为6cm,圆心角的度数为120°,若将此扇形围成一个圆锥,则:
(1)求出围成的圆锥的侧面积为多少?
(2)求出该圆锥的底面半径是多少?
16.如下示意图,是我市香菇培植场常见的半地下室栽培棚,它由两部分组成,地上部分为半圆柱形四周封闭的塑料薄膜保温棚;地下部分为长方体的培植室,室内长30米,宽1.2米的地面上存放菌棒培育香菇.
(1)地下培植室内按标准排放菌棒,宽排放8袋,长每米排放4排,求能排放多少袋香菇菌棒?
(2)要建这样的保温棚约需多少平方米的塑料薄膜?(不计余料及埋在土里的塑料薄膜,结果精确到0.1平方米)
17.有一个直径为1m的圆形铁皮,要从中剪出一个最大的圆心角为90°的扇形ABC,如图所示.
(1)求被剪掉阴影部分的面积:
(2)用所留的扇形铁皮围成一个圆锥,该圆锥的底面圆的半径是多少?
18.在数学活动课中,同学们准备了一些等腰直角三角形纸片,从每张纸片中剪出一个扇形制作圆锥玩具模型.如图,已知△ABC是腰长为16cm的等腰直角三角形.
(1)在等腰直角三角形ABC纸片中,以C为圆心,剪出一个面积最大的扇形(要求:尺规作图,保留作图痕迹,不写作法);
(2)请求出所制作圆锥底面的半径长.
19.如图,在正方形网格中建立平面直角坐标系,一条圆弧经过网格点A(0,8)、B(﹣8,8)、C(﹣12,4),请在网格图中进行如下操作:
(1)若该圆弧所在圆的圆心为D,则D点坐标为 ;
(2)连接AD、CD,则⊙D的半径长为 (结果保留根号).∠ADC的度数为 °;
(3)若扇形ADC是一个圆锥的侧面展开图,求该圆锥的底面圆的半径长.(结果保留根号)
20.某种冰激凌的外包装可以视为圆锥,它的底面圆直径ED与母线AD长之比为1:2.制作这种外包装需要用如图所示的等腰三角形材料,其中AB=AC,AD⊥BC.将扇形AEF围成圆锥时,AE,AF恰好重合.
(1)求这种加工材料的顶角∠BAC的大小.
(2)若圆锥底面圆的直径ED为5cm,求加工材料剩余部分(图中阴影部分)的面积.(结果保留π)
参考答案
1.解:设圆锥的底面圆半径为rcm,依题意,得
2πr=,
解得r=10.
故选:B.
2.解:∵⊙O的直径为2,则半径是:1,
∴S⊙O=π×12=π,
连接BC、AO,根据题意知BC⊥AO,AO=BO=1,
在Rt△ABO中,AB==,
即扇形的对应半径R=,
弧长l==,
设圆锥底面圆半径为r,则有
2πr=,
解得:r=.
故选:B.
3.解:设这个圆锥的底面圆的半径是rcm,
根据题意得2π?r=,
解得r=2,
即这个圆锥的底面圆的半径是2cm.
故选:A.
4.解:扇形的弧长==4π,
∴圆锥的底面半径为4π÷2π=2.
故选:A.
5.解:由题意一个圆锥的侧面展开图是面积为的半圆面,
因为π=πl2,所以母线长为l=1,
又半圆的弧长为π,
圆锥的底面的周长为2πr=π,
所以底面圆半径为r=,
所以该圆锥的高为h===,
故选:D.
6.解:设圆锥的底面的半径为rcm,
根据题意得=2πr,
解得r=1,
所以底面圆的直径为2cm,
故选:A.
7.解:∵圆柱的底面直径为2,
∴圆柱的底面周长为2π.
∵侧面积为8π,
∴圆柱的高为:8π÷2π=4,
故选:B.
8.解:∵圆柱的底面半径为10cm,
则其底面周长为:2π×10=20π(cm),
圆柱的高也是20π(cm),
故选:B.
9.解:设圆锥的底面圆的半径为r,
根据题意得2πr=,解得r=2,
这个圆锥的高h==4,
故选:D.
10.解:扇形的弧长是:=,
圆的半径r=1,则底面圆的周长是2π,
圆锥的底面周长等于侧面展开图的扇形弧长则得到:=2π,
∴=2,
即:R=4,
故选:C.
11.解:由三视图可知几何体底面半径为1,高为的圆锥,圆锥的母线长为=2.
所以所求几何体的表面积为:S侧+S底=π?1?2+π?12=3π,
故选:B.
12.解:设此圆锥的母线长为l,
根据题意得×2π×6×l=60π,解得l=10,
所以此圆锥的母线长为10.
故答案为10.
13.解:设圆锥的底面圆半径为r,依题意,得
2πr=,
解得r=.
故答案为:.
14.解:圆锥形的烟囱冒的侧面积=?80π?50=2000π(cm2),
100个这样的烟囱冒至少需要100×2000π=200000π(cm2),
故答案为200000π.
15.解:(1)圆锥的侧面积==12π(cm2);
(2)该圆锥的底面半径为r,
根据题意得2πr=,
解得r=2.
即圆锥的底面半径为2cm.
16.解:(1)宽排放8袋,长每米排放4排,共30米,所以培植室内能放8×4×30=960袋香菇菌棒;
(2)塑料棚的全面积为18π+0.36π=18.36π≈57.7.
∴要建这样的香菇保温棚需塑料薄膜57.7平方米.
17.解:(1)如图,连接BC,
∵∠BAC=90°,
∴BC为⊙O的直径,即BC=1m,
又∵AB=AC,
∴.
∴(平方米)
(2)设底面圆的半径为r,则,
∴.
圆锥的底面圆的半径长为米.
18.解:(1)如图所示:扇形CEF为所求作的图形;
(2)∵△ABC是等腰直角三角形,且AC=BC=16cm,
∴AB=16cm,
由(1)可知CD平分∠ACB,
∴CD⊥AB,
∴CD=8cm,
设圆锥底面的半径长为r,依题意得:2πr=,
∴r=2cm,
答:所制作圆锥底面的半径长为2cm.
19.解:(1)点D的坐标为(﹣4,0);
(2)如图,AD==4,
即⊙D的半径长为4;
∵AD=CD=4,AC==4,
∴AD2+DC2=AC2,
∴△ACD为直角三角形,∠ADC的度数为90°;
故答案为(﹣4,0);4;90;
(3)设该圆锥的底面圆的半径长为r,
根据题意得2πr=,解得r=,
即该圆锥的底面圆的半径长为.
20.解:(1)设∠BAC=n°.
由题意得π?DE=,AD=2DE,
∴n=90,
∴∠BAC=90°.
(2)∵AD=2DE=10(cm),
∴S阴=?BC?AD﹣S扇形AEF=×10×20﹣=(100﹣25π)cm2.
能力达标专题突破训练(附答案)
1.用半径为30cm,圆心角为120°的扇形纸片恰好能围成一个圆锥的侧面,则这个圆锥底面半径为( )
A.5cm B.10cm C.15cm D.20cm
2.如图,从一块直径是2的圆形铁片上剪出一个圆心角为90°的扇形,将剪下来的扇形围成一个圆锥.那么这个圆锥的底面圆的半径是( )
A. B. C. D.1
3.如图,已知扇形OAB的半径为6cm,圆心角的度数为120°,若将OA,OB重合后围成一圆锥侧面,那么圆锥的底面半径为( )
A.2cm B.3cm C.6cm D.2cm
4.用一个圆心角为120°,半径为6的扇形做成一个圆锥的侧面,则这个圆锥的底面圆的半径为( )
A.2 B.6 C.2 D.3
5.一个圆锥的侧面展开图是一个面积为的半圆,则该圆锥的高为( )
A..1 B.2 C. D.
6.如图所示,矩形纸片ABCD中,AB=4cm,把它分割成正方形纸片ABFE和矩形纸片EFCD后,分别裁出扇形ABF和半径最大的圆,恰好能作为一个圆锥的侧面和底面,则底面圆的直径的长为( )
A.2cm B.3cm C.4cm D.5cm
7.圆柱的底面直径为2,侧面积为8π,则圆柱的高为( )
A.2 B.4 C.6 D.1
8.一个圆柱的侧面展开图是一个正方形,它的底面半径为10cm,则这个圆柱的高为( )
A.10πcm B.20πcm C.10cm D.20cm
9.如图,在等腰△ABC中,∠BAC=120°,AD是∠BAC的角平分线,且AD=6,以点A为圆心,AD长为半径画弧,交AB于点E,交AC于点F,将阴影部分剪掉,余下扇形AEF,将扇形AEF围成一个圆锥的侧面,AE与AF正好重合,圆锥侧面无重叠,求这个圆锥的高为( )
A.2 B. C.4 D.
10.如图,在纸上剪一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型,若圆的半径r=1,扇形的半径为R,扇形的圆心角等于90°,则R的值是( )
A.R=2 B.R=3 C.R=4 D.R=5
11.如图是某几何体的三种视图,其表面积为( )
A.2π B.3π C.4π D.5π
12.某同学在数学实践活动中,制作了一个侧面积为60π,底面半径为6的圆锥模型(如图所示),则此圆锥的母线长为 .
13.用半径为50,圆心角为120°的扇形纸片围成一个圆锥的侧面,则这个圆锥的底面半径为 .
14.圆锥形的烟囱冒的底面直径是80cm,母线长是50cm,制作100个这样的烟囱冒至少需要 cm2的铁皮(结果保留π).
15.如图所示,已知扇形AOB的半径为6cm,圆心角的度数为120°,若将此扇形围成一个圆锥,则:
(1)求出围成的圆锥的侧面积为多少?
(2)求出该圆锥的底面半径是多少?
16.如下示意图,是我市香菇培植场常见的半地下室栽培棚,它由两部分组成,地上部分为半圆柱形四周封闭的塑料薄膜保温棚;地下部分为长方体的培植室,室内长30米,宽1.2米的地面上存放菌棒培育香菇.
(1)地下培植室内按标准排放菌棒,宽排放8袋,长每米排放4排,求能排放多少袋香菇菌棒?
(2)要建这样的保温棚约需多少平方米的塑料薄膜?(不计余料及埋在土里的塑料薄膜,结果精确到0.1平方米)
17.有一个直径为1m的圆形铁皮,要从中剪出一个最大的圆心角为90°的扇形ABC,如图所示.
(1)求被剪掉阴影部分的面积:
(2)用所留的扇形铁皮围成一个圆锥,该圆锥的底面圆的半径是多少?
18.在数学活动课中,同学们准备了一些等腰直角三角形纸片,从每张纸片中剪出一个扇形制作圆锥玩具模型.如图,已知△ABC是腰长为16cm的等腰直角三角形.
(1)在等腰直角三角形ABC纸片中,以C为圆心,剪出一个面积最大的扇形(要求:尺规作图,保留作图痕迹,不写作法);
(2)请求出所制作圆锥底面的半径长.
19.如图,在正方形网格中建立平面直角坐标系,一条圆弧经过网格点A(0,8)、B(﹣8,8)、C(﹣12,4),请在网格图中进行如下操作:
(1)若该圆弧所在圆的圆心为D,则D点坐标为 ;
(2)连接AD、CD,则⊙D的半径长为 (结果保留根号).∠ADC的度数为 °;
(3)若扇形ADC是一个圆锥的侧面展开图,求该圆锥的底面圆的半径长.(结果保留根号)
20.某种冰激凌的外包装可以视为圆锥,它的底面圆直径ED与母线AD长之比为1:2.制作这种外包装需要用如图所示的等腰三角形材料,其中AB=AC,AD⊥BC.将扇形AEF围成圆锥时,AE,AF恰好重合.
(1)求这种加工材料的顶角∠BAC的大小.
(2)若圆锥底面圆的直径ED为5cm,求加工材料剩余部分(图中阴影部分)的面积.(结果保留π)
参考答案
1.解:设圆锥的底面圆半径为rcm,依题意,得
2πr=,
解得r=10.
故选:B.
2.解:∵⊙O的直径为2,则半径是:1,
∴S⊙O=π×12=π,
连接BC、AO,根据题意知BC⊥AO,AO=BO=1,
在Rt△ABO中,AB==,
即扇形的对应半径R=,
弧长l==,
设圆锥底面圆半径为r,则有
2πr=,
解得:r=.
故选:B.
3.解:设这个圆锥的底面圆的半径是rcm,
根据题意得2π?r=,
解得r=2,
即这个圆锥的底面圆的半径是2cm.
故选:A.
4.解:扇形的弧长==4π,
∴圆锥的底面半径为4π÷2π=2.
故选:A.
5.解:由题意一个圆锥的侧面展开图是面积为的半圆面,
因为π=πl2,所以母线长为l=1,
又半圆的弧长为π,
圆锥的底面的周长为2πr=π,
所以底面圆半径为r=,
所以该圆锥的高为h===,
故选:D.
6.解:设圆锥的底面的半径为rcm,
根据题意得=2πr,
解得r=1,
所以底面圆的直径为2cm,
故选:A.
7.解:∵圆柱的底面直径为2,
∴圆柱的底面周长为2π.
∵侧面积为8π,
∴圆柱的高为:8π÷2π=4,
故选:B.
8.解:∵圆柱的底面半径为10cm,
则其底面周长为:2π×10=20π(cm),
圆柱的高也是20π(cm),
故选:B.
9.解:设圆锥的底面圆的半径为r,
根据题意得2πr=,解得r=2,
这个圆锥的高h==4,
故选:D.
10.解:扇形的弧长是:=,
圆的半径r=1,则底面圆的周长是2π,
圆锥的底面周长等于侧面展开图的扇形弧长则得到:=2π,
∴=2,
即:R=4,
故选:C.
11.解:由三视图可知几何体底面半径为1,高为的圆锥,圆锥的母线长为=2.
所以所求几何体的表面积为:S侧+S底=π?1?2+π?12=3π,
故选:B.
12.解:设此圆锥的母线长为l,
根据题意得×2π×6×l=60π,解得l=10,
所以此圆锥的母线长为10.
故答案为10.
13.解:设圆锥的底面圆半径为r,依题意,得
2πr=,
解得r=.
故答案为:.
14.解:圆锥形的烟囱冒的侧面积=?80π?50=2000π(cm2),
100个这样的烟囱冒至少需要100×2000π=200000π(cm2),
故答案为200000π.
15.解:(1)圆锥的侧面积==12π(cm2);
(2)该圆锥的底面半径为r,
根据题意得2πr=,
解得r=2.
即圆锥的底面半径为2cm.
16.解:(1)宽排放8袋,长每米排放4排,共30米,所以培植室内能放8×4×30=960袋香菇菌棒;
(2)塑料棚的全面积为18π+0.36π=18.36π≈57.7.
∴要建这样的香菇保温棚需塑料薄膜57.7平方米.
17.解:(1)如图,连接BC,
∵∠BAC=90°,
∴BC为⊙O的直径,即BC=1m,
又∵AB=AC,
∴.
∴(平方米)
(2)设底面圆的半径为r,则,
∴.
圆锥的底面圆的半径长为米.
18.解:(1)如图所示:扇形CEF为所求作的图形;
(2)∵△ABC是等腰直角三角形,且AC=BC=16cm,
∴AB=16cm,
由(1)可知CD平分∠ACB,
∴CD⊥AB,
∴CD=8cm,
设圆锥底面的半径长为r,依题意得:2πr=,
∴r=2cm,
答:所制作圆锥底面的半径长为2cm.
19.解:(1)点D的坐标为(﹣4,0);
(2)如图,AD==4,
即⊙D的半径长为4;
∵AD=CD=4,AC==4,
∴AD2+DC2=AC2,
∴△ACD为直角三角形,∠ADC的度数为90°;
故答案为(﹣4,0);4;90;
(3)设该圆锥的底面圆的半径长为r,
根据题意得2πr=,解得r=,
即该圆锥的底面圆的半径长为.
20.解:(1)设∠BAC=n°.
由题意得π?DE=,AD=2DE,
∴n=90,
∴∠BAC=90°.
(2)∵AD=2DE=10(cm),
∴S阴=?BC?AD﹣S扇形AEF=×10×20﹣=(100﹣25π)cm2.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
