第2章轴对称图形 优生辅导专题提升训练 2021-2022学年苏科版八年级数学上册(Word版 含答案)
文档属性
| 名称 | 第2章轴对称图形 优生辅导专题提升训练 2021-2022学年苏科版八年级数学上册(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 240.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-16 15:23:11 | ||
图片预览

文档简介
2021-2022学年苏科版八年级数学上册《第2章轴对称图形》优生辅导
专题提升训练(附答案)
1.在Rt△ABC中,∠B=90°,AD平分∠BAC,交BC于点D,DE⊥AC,垂足为点E,若BD=3,则DE的长为( )
A.3 B. C.2 D.6
2.如图,在△ABC中,AB的垂直平分线交AB于点D,交BC于点E,连接AE.若BC=6,AC=5,则△ACE的周长为( )
A.8 B.11 C.16 D.17
3.已知等腰三角形的一边长等于4,一边长等于9,则它的周长为( )
A.9 B.17或22 C.17 D.22
4.已知△ABC的三边长分别为4、4、6,在△ABC所在平面内画一条直线,将△ABC分割成两个三角形,使其中的一个是等腰三角形,则这样的直线最多可画( )条.
A.3 B.4 C.5 D.6
5.如图,在△ABC中,AB=AC,∠C=65°,点D是BC边上任意一点,过点D作DF∥AB交AC于点E,则∠FEC的度数是( )
A.120° B.130° C.145° D.150°
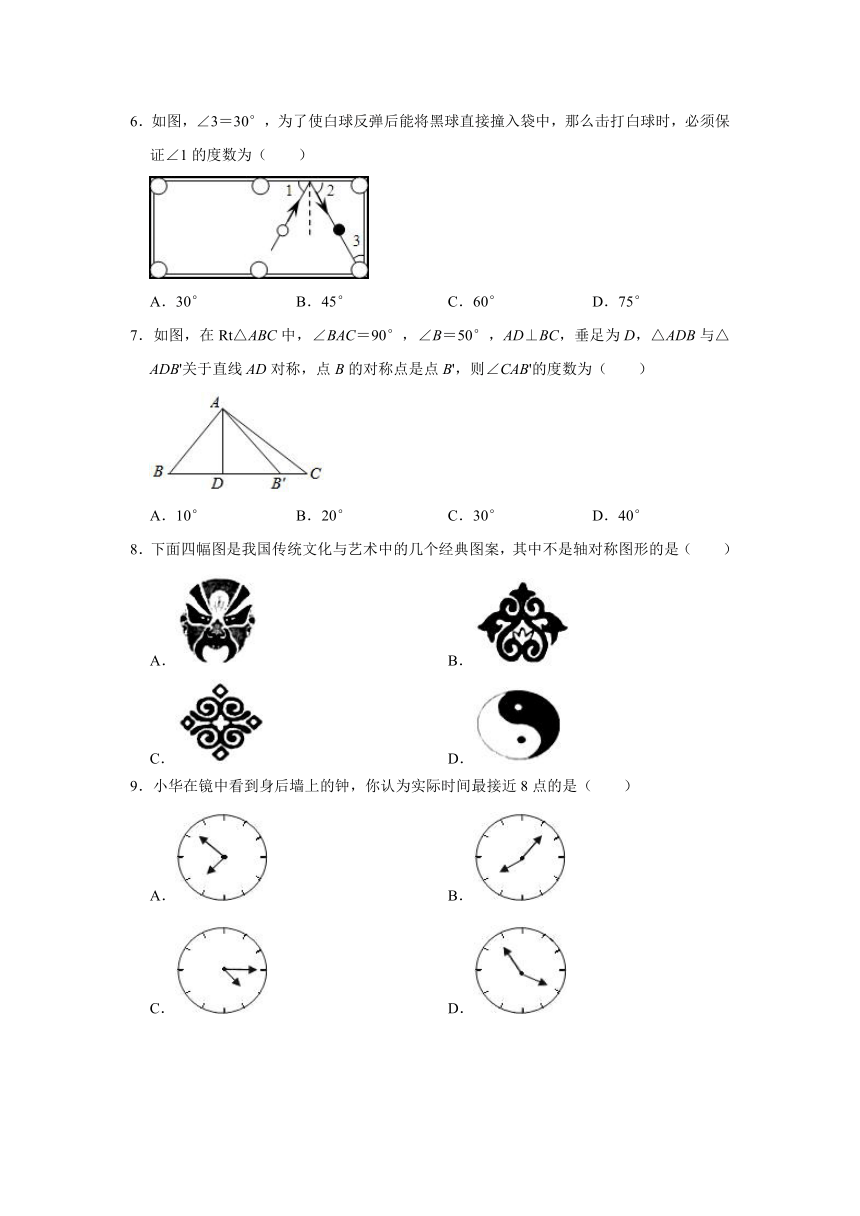
6.如图,∠3=30°,为了使白球反弹后能将黑球直接撞入袋中,那么击打白球时,必须保证∠1的度数为( )
A.30° B.45° C.60° D.75°
7.如图,在Rt△ABC中,∠BAC=90°,∠B=50°,AD⊥BC,垂足为D,△ADB与△ADB'关于直线AD对称,点B的对称点是点B',则∠CAB'的度数为( )
A.10° B.20° C.30° D.40°
8.下面四幅图是我国传统文化与艺术中的几个经典图案,其中不是轴对称图形的是( )
A. B.
C. D.
9.小华在镜中看到身后墙上的钟,你认为实际时间最接近8点的是( )
A. B.
C. D.
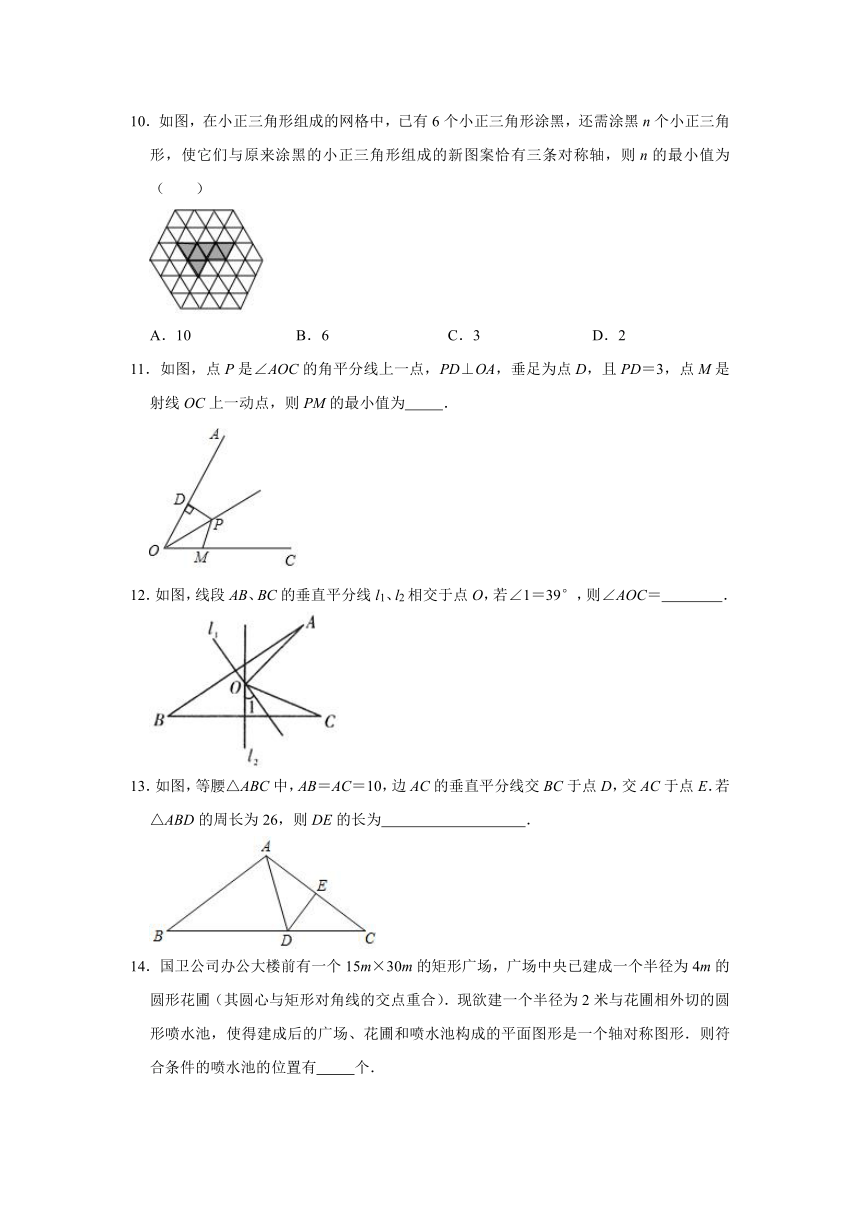
10.如图,在小正三角形组成的网格中,已有6个小正三角形涂黑,还需涂黑n个小正三角形,使它们与原来涂黑的小正三角形组成的新图案恰有三条对称轴,则n的最小值为( )
A.10 B.6 C.3 D.2
11.如图,点P是∠AOC的角平分线上一点,PD⊥OA,垂足为点D,且PD=3,点M是射线OC上一动点,则PM的最小值为 .
12.如图,线段AB、BC的垂直平分线l1、l2相交于点O,若∠1=39°,则∠AOC= .
13.如图,等腰△ABC中,AB=AC=10,边AC的垂直平分线交BC于点D,交AC于点E.若△ABD的周长为26,则DE的长为 .
14.国卫公司办公大楼前有一个15m×30m的矩形广场,广场中央已建成一个半径为4m的圆形花圃(其圆心与矩形对角线的交点重合).现欲建一个半径为2米与花圃相外切的圆形喷水池,使得建成后的广场、花圃和喷水池构成的平面图形是一个轴对称图形.则符合条件的喷水池的位置有 个.
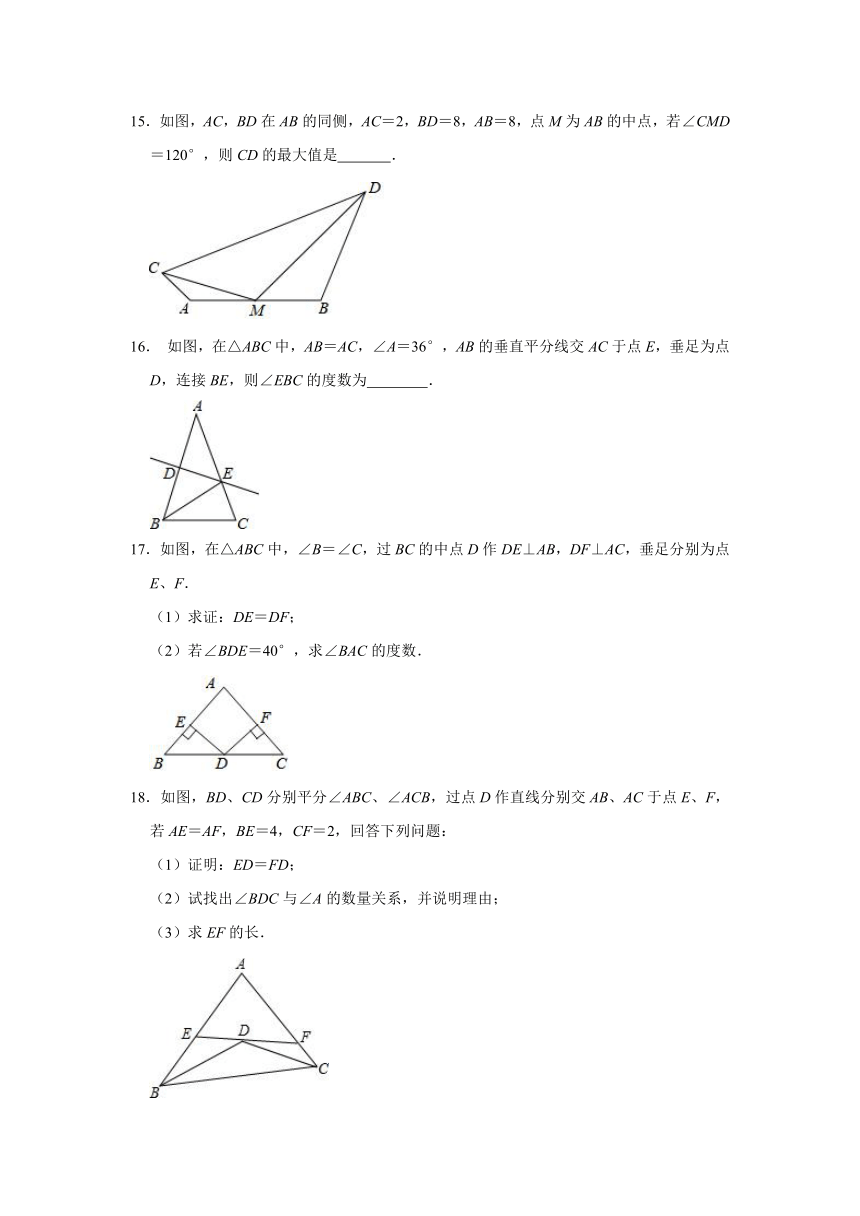
15.如图,AC,BD在AB的同侧,AC=2,BD=8,AB=8,点M为AB的中点,若∠CMD=120°,则CD的最大值是 .
16. 如图,在△ABC中,AB=AC,∠A=36°,AB的垂直平分线交AC于点E,垂足为点D,连接BE,则∠EBC的度数为 .
17.如图,在△ABC中,∠B=∠C,过BC的中点D作DE⊥AB,DF⊥AC,垂足分别为点E、F.
(1)求证:DE=DF;
(2)若∠BDE=40°,求∠BAC的度数.
18.如图,BD、CD分别平分∠ABC、∠ACB,过点D作直线分别交AB、AC于点E、F,若AE=AF,BE=4,CF=2,回答下列问题:
(1)证明:ED=FD;
(2)试找出∠BDC与∠A的数量关系,并说明理由;
(3)求EF的长.
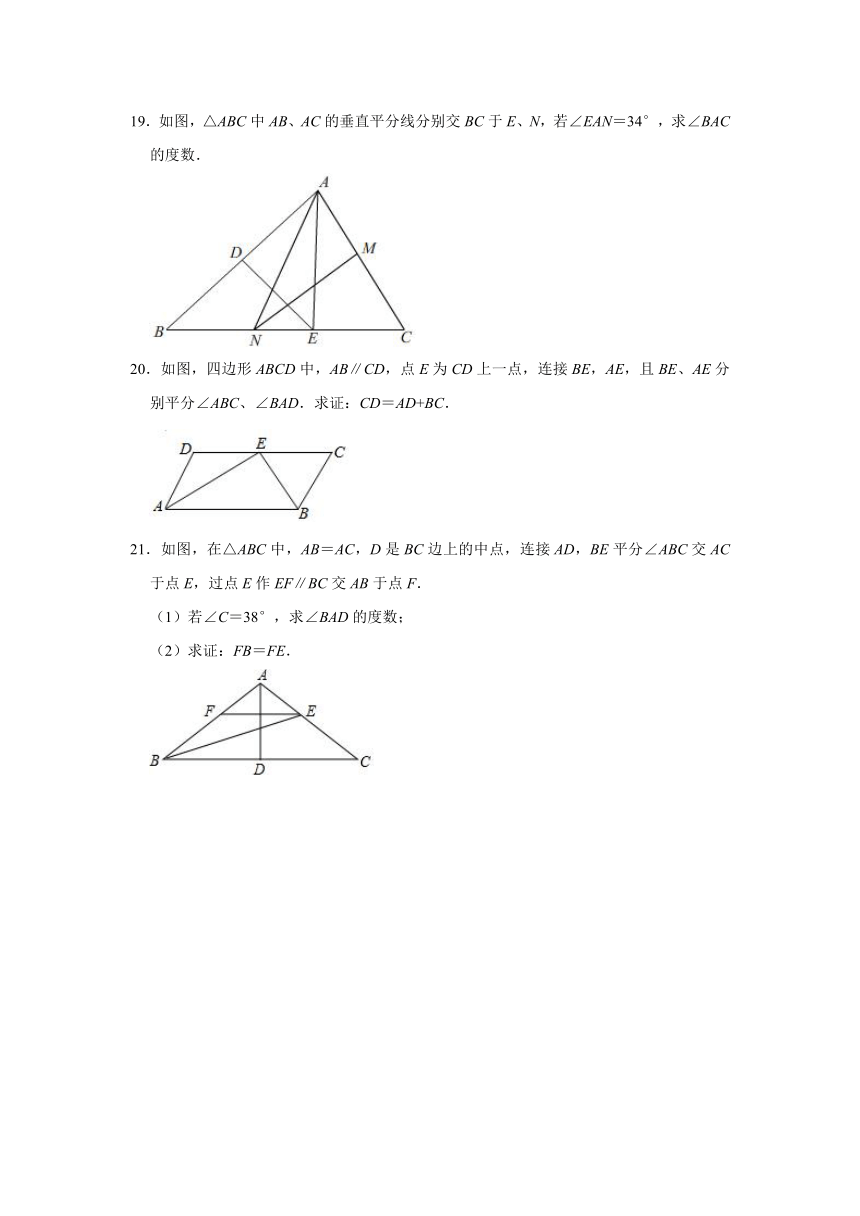
19.如图,△ABC中AB、AC的垂直平分线分别交BC于E、N,若∠EAN=34°,求∠BAC的度数.
20.如图,四边形ABCD中,AB∥CD,点E为CD上一点,连接BE,AE,且BE、AE分别平分∠ABC、∠BAD.求证:CD=AD+BC.
21.如图,在△ABC中,AB=AC,D是BC边上的中点,连接AD,BE平分∠ABC交AC于点E,过点E作EF∥BC交AB于点F.
(1)若∠C=38°,求∠BAD的度数;
(2)求证:FB=FE.
参考答案
1.解:∵∠B=90°,
∴DB⊥AB,
又∵AD平分∠BAC,DE⊥AC,
∴DE=BD=3,
故选:A.
2.解:∵DE垂直平分AB,
∴AE=BE,
∴△ACE的周长=AC+CE+AE
=AC+CE+BE
=AC+BC
=5+6
=11.
故选:B.
3.解:分两种情况:
当腰为4时,4+4<9,所以不能构成三角形;
当腰为9时,9+9>4,9﹣9<4,所以能构成三角形,周长是:9+9+4=22.
故选:D.
4.解:如图所示:
当AC=CD,AB=BG,AF=CF,AE=BE时,都能得到符合题意的等腰三角形(AD,AE,AF,AG分别为分割线).
故选:B.
5.解:∵AB=AC,∠C=65°,
∴∠B=∠C=65°,
∵DF∥AB,
∴∠CDE=∠B=65°,
∴∠FEC=∠CDE+∠C=65°+65°=130°;
故选:B.
6.解:要使白球反弹后能将黑球直接撞入袋中,
∠2+∠3=90°,
∵∠3=30°,
∴∠2=60°,
∴∠1=60°.
故选:C.
7.解:∵∠BAC=90°,∠B=50°,
∴∠C=40°,
∵△ADB与△ADB'关于直线AD对称,点B的对称点是点B',
∴∠AB'B=∠B=50°,
∴∠CAB'=∠AB'B﹣∠C=10°,
故选:A.
8.解:A、是轴对称图形,故此选项不合题意;
B、是轴对称图形,故此选项不合题意;
C、是轴对称图形,故此选项不符合题意;
D、不是轴对称图形,故此选项符合题意;
故选:D.
9.解:实际时间为8点的时针关于过12时、6时的直线的对称点是4点,
那么8点的时钟在镜子中看来应该是4点的样子,
所以应该是C或D答案之一,这两个答案中更接近八点的应该是第四个图形.
故选:D.
10.解:如图所示,n的最小值为3,
故选:C.
11.解:根据垂线段最短可知:当PM⊥OC时,PM最小,
当PM⊥OC时,
又∵OP平分∠AOC,PD⊥OA,PD=3,
∴PM=PD=3,
故答案为:3.
12.解:解法一:连接BO,并延长BO到P,
∵线段AB、BC的垂直平分线l1、l2相交于点O,
∴AO=OB=OC,∠BDO=∠BEO=90°,
∴∠DOE+∠ABC=180°,
∵∠DOE+∠1=180°,
∴∠ABC=∠1=39°,
∵OA=OB=OC,
∴∠A=∠ABO,∠OBC=∠C,
∵∠AOP=∠A+∠ABO,∠COP=∠C+∠OBC,
∴∠AOC=∠AOP+∠COP=∠A+∠ABC+∠C=2×39°=78°;
解法二:
连接OB,
∵线段AB、BC的垂直平分线l1、l2相交于点O,
∴AO=OB=OC,
∴∠AOD=∠BOD,∠BOE=∠COE,
∵∠DOE+∠1=180°,∠1=39°,
∴∠DOE=141°,即∠BOD+∠BOE=141°,
∴∠AOD+∠COE=141°,
∴∠AOC=360°﹣(∠BOD+∠BOE)﹣(∠AOD+∠COE)=78°;
故答案为:78°.
13.解:作AM⊥BC于M,
∵边AC的垂直平分线交BC于点D,交AC于点E,
∴∠AED=90°,AE=CE=AC==5,AD=CD,
∴∠DAC=∠C,
∵△ABD的周长为26,
∴AB+BD+AD=AB+BD+CD=AB+BC=26,
∵AB=AC=10,
∴BC=16,∠B=∠C,
∴∠B=∠DAC,
∵∠ACB=∠DCA,
∵AB=AC,
∴BM=BC=8,
∴AM=6,
∴DE=,
故答案为.
14.解:花圃建后整个图形还是轴对称图形,再建一个圆形喷水池后要使整个图形仍然是轴对称图形,喷水池的位置只能是建在花圃与矩形四边最靠近的地方,共有四种选择,但要考虑半径的大小.因为花圃半径4米,矩形宽15米,所以花圃与矩形长边的最小距离是3.5米,与短边的最小距离是11米,故要建半径2米的喷水池的位置只有2个.
15.解:如图,作点A关于CM的对称点A′,点B关于DM的对称点B′,连接CA'、MA'、MB'、A'B'、B'D,
∵∠CMD=120°,
∴∠AMC+∠DMB=60°,
∴∠CMA′+∠DMB′=60°,
∴∠A′MB′=60°,
∵MA′=MB′,
∴△A′MB′为等边三角形
∵CD≤CA′+A′B′+B′D=CA+AM+BD=2+4+8=14,
∴CD的最大值为14,
故答案为14.
16.解:∵DE是AB的垂直平分线,
∴AE=BE,
∴∠ABE=∠A=36°,
∵AB=AC,
∴∠ABC=∠C==72°,
∴∠EBC=∠ABC﹣∠ABE=72°﹣36°=36°.
故答案为:36°.
17.(1)证明:∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°,
∵D是BC的中点,
∴BD=CD,
在△BED与△CFD中,
,
∴△BED≌△CFD(AAS),
∴DE=DF;
(2)解:∵∠BDE=40°,
∴∠B=50°,
∴∠C=50°,
∴∠BAC=80°.
18.(1)证明:过D点分别作DG⊥BC,DK⊥AB,DH⊥AC,垂足分别为G,K,H,如图,
∴∠EKD=∠FHD=90°,
∵BD平分∠ABC,CD平分∠ACB,
∴DK=DG=DH,
在△EKD和△FHD中,
,
∵AE=AF
∴∠AEF=∠AFE,
∴△EKD≌△FHD(AAS),
∴ED=FD;
(2)解:∠BDC=90°+∠A.
理由如下:
∵BD平分∠ABC,CD平分∠ACB,
∴∠DBC=∠ABC,∠DCB=∠ACB,
∴∠DBC+∠DCB=(∠ABC+∠ACB),
∵∠BDC+∠DBC+∠DCB=180°,
∴∠BDC+(∠ABC+∠ACB)=180°,
∵∠A+∠ABC+∠ACB=180°,
∴∠ABC+∠ACB=180°﹣∠A,
∴∠BDC+(180°﹣∠A)=180°,
∴∠BDC=90°+∠A;
(3)解:如图,
∵BD,CD分别平分∠ABC,∠ACB,
∴∠1=∠2,∠3=∠4,
∵∠2+∠7+∠4=180°,∠5+∠6+∠7=180°,
∴∠2+∠4=∠5+∠6,即∠1+∠3=∠5+∠6,
∵∠AEF=∠AFE,
∴∠1+∠5=∠3+∠6,
∴∠5=∠3,∠1=∠6,
∴△BED∽△CED,
∴ED:CF=BE:DF,
∵DE=DF,
则ED2=CF?BE=2×4=8,
则ED=,
∴EF=2ED=.
19.解:∵AB、AC的垂直平分线分别交BC于点E、N,
∴AE=BE,AN=CN,
∴∠BAE=∠B,∠CAN=∠C,
∵∠AEC=∠BAE+∠B=2∠BAE,∠ANB=∠CAN+∠C=2∠CAN,
∵∠EAN=34°,
∴∠AEN+∠ANE=180°﹣∠EAN=146°,
∵∠AEN=180°﹣2∠BAE,∠ANE=180°﹣2∠CAN,
∴180°﹣2∠BAE+180°﹣2∠CAN=146°,
∴∠B+∠C=107°,
∴∠BAC=180°﹣107°=73°.
20.证明:∵AE平分∠DAB,BE平分∠ABC,
∴∠DAE=∠BAE,∠ABE=∠EBC,
∵AB∥CD,
∴∠BAE=∠DEA,∠ABE=∠BEC,
∴∠DAE=∠DEA,∠EBC=∠BEC,
∴AD=DE,BC=CE.
∴CD=DE+CE=AD+BC.
21.解:(1)∵AB=AC,
∴∠C=∠ABC=38°,
∵D为BC的中点,AB=AC,
∴AD⊥BC,即∠ADB=90°,
∴∠BAD=90°﹣∠ABC=90°﹣38°=52°.
(2)∵BE平分∠ABC,
∴∠EBF=∠EBC,
∵EF∥BC,
∴∠EBC=∠BEF,
∴∠EBF=∠FEB,
∴BF=EF.
专题提升训练(附答案)
1.在Rt△ABC中,∠B=90°,AD平分∠BAC,交BC于点D,DE⊥AC,垂足为点E,若BD=3,则DE的长为( )
A.3 B. C.2 D.6
2.如图,在△ABC中,AB的垂直平分线交AB于点D,交BC于点E,连接AE.若BC=6,AC=5,则△ACE的周长为( )
A.8 B.11 C.16 D.17
3.已知等腰三角形的一边长等于4,一边长等于9,则它的周长为( )
A.9 B.17或22 C.17 D.22
4.已知△ABC的三边长分别为4、4、6,在△ABC所在平面内画一条直线,将△ABC分割成两个三角形,使其中的一个是等腰三角形,则这样的直线最多可画( )条.
A.3 B.4 C.5 D.6
5.如图,在△ABC中,AB=AC,∠C=65°,点D是BC边上任意一点,过点D作DF∥AB交AC于点E,则∠FEC的度数是( )
A.120° B.130° C.145° D.150°
6.如图,∠3=30°,为了使白球反弹后能将黑球直接撞入袋中,那么击打白球时,必须保证∠1的度数为( )
A.30° B.45° C.60° D.75°
7.如图,在Rt△ABC中,∠BAC=90°,∠B=50°,AD⊥BC,垂足为D,△ADB与△ADB'关于直线AD对称,点B的对称点是点B',则∠CAB'的度数为( )
A.10° B.20° C.30° D.40°
8.下面四幅图是我国传统文化与艺术中的几个经典图案,其中不是轴对称图形的是( )
A. B.
C. D.
9.小华在镜中看到身后墙上的钟,你认为实际时间最接近8点的是( )
A. B.
C. D.
10.如图,在小正三角形组成的网格中,已有6个小正三角形涂黑,还需涂黑n个小正三角形,使它们与原来涂黑的小正三角形组成的新图案恰有三条对称轴,则n的最小值为( )
A.10 B.6 C.3 D.2
11.如图,点P是∠AOC的角平分线上一点,PD⊥OA,垂足为点D,且PD=3,点M是射线OC上一动点,则PM的最小值为 .
12.如图,线段AB、BC的垂直平分线l1、l2相交于点O,若∠1=39°,则∠AOC= .
13.如图,等腰△ABC中,AB=AC=10,边AC的垂直平分线交BC于点D,交AC于点E.若△ABD的周长为26,则DE的长为 .
14.国卫公司办公大楼前有一个15m×30m的矩形广场,广场中央已建成一个半径为4m的圆形花圃(其圆心与矩形对角线的交点重合).现欲建一个半径为2米与花圃相外切的圆形喷水池,使得建成后的广场、花圃和喷水池构成的平面图形是一个轴对称图形.则符合条件的喷水池的位置有 个.
15.如图,AC,BD在AB的同侧,AC=2,BD=8,AB=8,点M为AB的中点,若∠CMD=120°,则CD的最大值是 .
16. 如图,在△ABC中,AB=AC,∠A=36°,AB的垂直平分线交AC于点E,垂足为点D,连接BE,则∠EBC的度数为 .
17.如图,在△ABC中,∠B=∠C,过BC的中点D作DE⊥AB,DF⊥AC,垂足分别为点E、F.
(1)求证:DE=DF;
(2)若∠BDE=40°,求∠BAC的度数.
18.如图,BD、CD分别平分∠ABC、∠ACB,过点D作直线分别交AB、AC于点E、F,若AE=AF,BE=4,CF=2,回答下列问题:
(1)证明:ED=FD;
(2)试找出∠BDC与∠A的数量关系,并说明理由;
(3)求EF的长.
19.如图,△ABC中AB、AC的垂直平分线分别交BC于E、N,若∠EAN=34°,求∠BAC的度数.
20.如图,四边形ABCD中,AB∥CD,点E为CD上一点,连接BE,AE,且BE、AE分别平分∠ABC、∠BAD.求证:CD=AD+BC.
21.如图,在△ABC中,AB=AC,D是BC边上的中点,连接AD,BE平分∠ABC交AC于点E,过点E作EF∥BC交AB于点F.
(1)若∠C=38°,求∠BAD的度数;
(2)求证:FB=FE.
参考答案
1.解:∵∠B=90°,
∴DB⊥AB,
又∵AD平分∠BAC,DE⊥AC,
∴DE=BD=3,
故选:A.
2.解:∵DE垂直平分AB,
∴AE=BE,
∴△ACE的周长=AC+CE+AE
=AC+CE+BE
=AC+BC
=5+6
=11.
故选:B.
3.解:分两种情况:
当腰为4时,4+4<9,所以不能构成三角形;
当腰为9时,9+9>4,9﹣9<4,所以能构成三角形,周长是:9+9+4=22.
故选:D.
4.解:如图所示:
当AC=CD,AB=BG,AF=CF,AE=BE时,都能得到符合题意的等腰三角形(AD,AE,AF,AG分别为分割线).
故选:B.
5.解:∵AB=AC,∠C=65°,
∴∠B=∠C=65°,
∵DF∥AB,
∴∠CDE=∠B=65°,
∴∠FEC=∠CDE+∠C=65°+65°=130°;
故选:B.
6.解:要使白球反弹后能将黑球直接撞入袋中,
∠2+∠3=90°,
∵∠3=30°,
∴∠2=60°,
∴∠1=60°.
故选:C.
7.解:∵∠BAC=90°,∠B=50°,
∴∠C=40°,
∵△ADB与△ADB'关于直线AD对称,点B的对称点是点B',
∴∠AB'B=∠B=50°,
∴∠CAB'=∠AB'B﹣∠C=10°,
故选:A.
8.解:A、是轴对称图形,故此选项不合题意;
B、是轴对称图形,故此选项不合题意;
C、是轴对称图形,故此选项不符合题意;
D、不是轴对称图形,故此选项符合题意;
故选:D.
9.解:实际时间为8点的时针关于过12时、6时的直线的对称点是4点,
那么8点的时钟在镜子中看来应该是4点的样子,
所以应该是C或D答案之一,这两个答案中更接近八点的应该是第四个图形.
故选:D.
10.解:如图所示,n的最小值为3,
故选:C.
11.解:根据垂线段最短可知:当PM⊥OC时,PM最小,
当PM⊥OC时,
又∵OP平分∠AOC,PD⊥OA,PD=3,
∴PM=PD=3,
故答案为:3.
12.解:解法一:连接BO,并延长BO到P,
∵线段AB、BC的垂直平分线l1、l2相交于点O,
∴AO=OB=OC,∠BDO=∠BEO=90°,
∴∠DOE+∠ABC=180°,
∵∠DOE+∠1=180°,
∴∠ABC=∠1=39°,
∵OA=OB=OC,
∴∠A=∠ABO,∠OBC=∠C,
∵∠AOP=∠A+∠ABO,∠COP=∠C+∠OBC,
∴∠AOC=∠AOP+∠COP=∠A+∠ABC+∠C=2×39°=78°;
解法二:
连接OB,
∵线段AB、BC的垂直平分线l1、l2相交于点O,
∴AO=OB=OC,
∴∠AOD=∠BOD,∠BOE=∠COE,
∵∠DOE+∠1=180°,∠1=39°,
∴∠DOE=141°,即∠BOD+∠BOE=141°,
∴∠AOD+∠COE=141°,
∴∠AOC=360°﹣(∠BOD+∠BOE)﹣(∠AOD+∠COE)=78°;
故答案为:78°.
13.解:作AM⊥BC于M,
∵边AC的垂直平分线交BC于点D,交AC于点E,
∴∠AED=90°,AE=CE=AC==5,AD=CD,
∴∠DAC=∠C,
∵△ABD的周长为26,
∴AB+BD+AD=AB+BD+CD=AB+BC=26,
∵AB=AC=10,
∴BC=16,∠B=∠C,
∴∠B=∠DAC,
∵∠ACB=∠DCA,
∵AB=AC,
∴BM=BC=8,
∴AM=6,
∴DE=,
故答案为.
14.解:花圃建后整个图形还是轴对称图形,再建一个圆形喷水池后要使整个图形仍然是轴对称图形,喷水池的位置只能是建在花圃与矩形四边最靠近的地方,共有四种选择,但要考虑半径的大小.因为花圃半径4米,矩形宽15米,所以花圃与矩形长边的最小距离是3.5米,与短边的最小距离是11米,故要建半径2米的喷水池的位置只有2个.
15.解:如图,作点A关于CM的对称点A′,点B关于DM的对称点B′,连接CA'、MA'、MB'、A'B'、B'D,
∵∠CMD=120°,
∴∠AMC+∠DMB=60°,
∴∠CMA′+∠DMB′=60°,
∴∠A′MB′=60°,
∵MA′=MB′,
∴△A′MB′为等边三角形
∵CD≤CA′+A′B′+B′D=CA+AM+BD=2+4+8=14,
∴CD的最大值为14,
故答案为14.
16.解:∵DE是AB的垂直平分线,
∴AE=BE,
∴∠ABE=∠A=36°,
∵AB=AC,
∴∠ABC=∠C==72°,
∴∠EBC=∠ABC﹣∠ABE=72°﹣36°=36°.
故答案为:36°.
17.(1)证明:∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°,
∵D是BC的中点,
∴BD=CD,
在△BED与△CFD中,
,
∴△BED≌△CFD(AAS),
∴DE=DF;
(2)解:∵∠BDE=40°,
∴∠B=50°,
∴∠C=50°,
∴∠BAC=80°.
18.(1)证明:过D点分别作DG⊥BC,DK⊥AB,DH⊥AC,垂足分别为G,K,H,如图,
∴∠EKD=∠FHD=90°,
∵BD平分∠ABC,CD平分∠ACB,
∴DK=DG=DH,
在△EKD和△FHD中,
,
∵AE=AF
∴∠AEF=∠AFE,
∴△EKD≌△FHD(AAS),
∴ED=FD;
(2)解:∠BDC=90°+∠A.
理由如下:
∵BD平分∠ABC,CD平分∠ACB,
∴∠DBC=∠ABC,∠DCB=∠ACB,
∴∠DBC+∠DCB=(∠ABC+∠ACB),
∵∠BDC+∠DBC+∠DCB=180°,
∴∠BDC+(∠ABC+∠ACB)=180°,
∵∠A+∠ABC+∠ACB=180°,
∴∠ABC+∠ACB=180°﹣∠A,
∴∠BDC+(180°﹣∠A)=180°,
∴∠BDC=90°+∠A;
(3)解:如图,
∵BD,CD分别平分∠ABC,∠ACB,
∴∠1=∠2,∠3=∠4,
∵∠2+∠7+∠4=180°,∠5+∠6+∠7=180°,
∴∠2+∠4=∠5+∠6,即∠1+∠3=∠5+∠6,
∵∠AEF=∠AFE,
∴∠1+∠5=∠3+∠6,
∴∠5=∠3,∠1=∠6,
∴△BED∽△CED,
∴ED:CF=BE:DF,
∵DE=DF,
则ED2=CF?BE=2×4=8,
则ED=,
∴EF=2ED=.
19.解:∵AB、AC的垂直平分线分别交BC于点E、N,
∴AE=BE,AN=CN,
∴∠BAE=∠B,∠CAN=∠C,
∵∠AEC=∠BAE+∠B=2∠BAE,∠ANB=∠CAN+∠C=2∠CAN,
∵∠EAN=34°,
∴∠AEN+∠ANE=180°﹣∠EAN=146°,
∵∠AEN=180°﹣2∠BAE,∠ANE=180°﹣2∠CAN,
∴180°﹣2∠BAE+180°﹣2∠CAN=146°,
∴∠B+∠C=107°,
∴∠BAC=180°﹣107°=73°.
20.证明:∵AE平分∠DAB,BE平分∠ABC,
∴∠DAE=∠BAE,∠ABE=∠EBC,
∵AB∥CD,
∴∠BAE=∠DEA,∠ABE=∠BEC,
∴∠DAE=∠DEA,∠EBC=∠BEC,
∴AD=DE,BC=CE.
∴CD=DE+CE=AD+BC.
21.解:(1)∵AB=AC,
∴∠C=∠ABC=38°,
∵D为BC的中点,AB=AC,
∴AD⊥BC,即∠ADB=90°,
∴∠BAD=90°﹣∠ABC=90°﹣38°=52°.
(2)∵BE平分∠ABC,
∴∠EBF=∠EBC,
∵EF∥BC,
∴∠EBC=∠BEF,
∴∠EBF=∠FEB,
∴BF=EF.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
